Skip to main content
SpringerLink
Log in

Bifurcation and stability analysis in predator–prey model with a stage-structure for predator

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

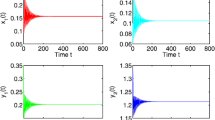
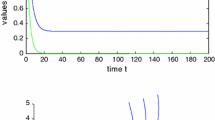
A predator–prey system with Holling type II functional response and stage-structure for predator is presented. The stability and Hopf bifurcation of this model are studied by analyzing the associated characteristic transcendental equation. Further, an explicit formula for determining the stability and the direction of periodic solutions bifurcating from positive equilibrium is derived by the normal form theory and center manifold argument. Some numerical simulations are also given to illustrate our results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Hale, J.K.: Theory of Functional Differential Equations. Springer, New York (1977)

    MATH  Google Scholar 

  2. Chen, F.D., : Permanence of a nonlinear integro-differential prey-competition model with infinite delays. Commun. Nonlinear Sci. Numer. Simul. 13, 2290–2297 (2008)

    Article  MathSciNet  Google Scholar 

  3. Huo, H.F., Li, W.T., Liu, X.: Existence and global attractivity of positive periodic solutions of an impulsive delay differential equation. Appl. Anal. 83, 1279–1290 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  4. Kuang, Y.: Delay Differential Equations with Applications in Population Dynamics. Mathematics in Science and Engineering, vol. 191. Academic Press, Boston (1993)

    Book  MATH  Google Scholar 

  5. Xiao, Y.N., Chen, L.S.: Modeling and analysis of a predator–prey model with disease in the prey. Math. Bios. 171, 59–82 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  6. Yan, J.R., Zhao, A.M.: Oscillation and stability of linear impulsive delay differential equations. J. Math. Anal. Appl. 227, 187–194 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  7. Chen, F.D., You, M.S.: Permanence, extinction and periodic solution of the predator–prey system with Beddington–DeAngelis functional response and stage structure for prey. Nonlinear Anal. Real World Appl. 9, 207–221 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  8. Chen, F.D., Chen, Y., Shi, J.: Stability of the boundary solution of a non-autonomous predator–prey system with the Beddington–DeAngelis functional response. J. Math. Anal. Appl. 344, 1057–1067 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  9. Sun, X.K., : Permanence of a Holling type II predator–prey system with stage-structure. In: Proceedings of the 6th Conference of Biomathematics, Tai’an, P.R. China, July. Adv. Biomath. 2, 598–602 (2008)

    Google Scholar 

  10. Song, X.Y., Hao, M.Y., Meng, X.Z.: A stage-structured predator–prey model with disturbing pulse and time delays. Appl. Math. Model. 33, 211–223 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  11. Wang, W.D., : Mathematical models of innovation diffusion with stage structure. Appl. Math. Model. 30, 129–146 (2006)

    Article  MATH  Google Scholar 

  12. Song, X.Y., Chen, L.S.: Optimal harvesting and stability for a predator–prey system model with age structure. Acta Math. Appl. Sinica 18, 423–430 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  13. Tang, S.Y., Chen, L.S.: Multiple attractors in stage-structured population models with birth pulses. Bull. Math. Biol. 65, 479–495 (2003)

    Article  Google Scholar 

  14. Satio, Y., Takeuchi, Y.: A time-delay model for prey–predator growth with stage structure. Can. Appl. Math. Q. 11, 293–302 (2003)

    MathSciNet  Google Scholar 

  15. Xiao, Y.N., Cheng, D.Z., Tang, S.Y.: Dynamic complexities in predator–prey ecosystem models with age-structure for predator. Chaos Solitons Fractals 14, 1403–1411 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  16. Qu, Y., Wei, J.J.: Bifurcation analysis in a time-delay model for prey–predator growth with stage-structure. Nonlinear Dyn. 49, 285–294 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  17. Gourley, S.A., Kuang, Y.: A stage structured predator–prey model and its dependence on maturation delay and death rate. J. Math. Biol. 49, 188–200 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  18. Liu, S.Q., Beretta, E.: A stage-structured predator–prey model of Beddington–DeAngelis type. SIAM J. Appl. Math. 66, 1101–1129 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  19. Beretta, E., Kuang, Y.: Geometric stability switch criteria in delay differential systems with delay dependent parameters. SIAM J. Math. Anal. 33, 1144–1165 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  20. Hassard, B., Kazarinoff, N., Wan, Y.: Theory and Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Applied Mathematics, Lanzhou University of Technology, Lanzhou, Gansu, 730050, People’s Republic of China

    Xiao-Ke Sun, Hai-Feng Huo & Hong Xiang

  2. School of Mathematics and Statistics, Tianshui Normal University, Tianshui, Gansu, 741001, People’s Republic of China

    Xiao-Ke Sun

Authors
  1. Xiao-Ke Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hai-Feng Huo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hong Xiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hai-Feng Huo.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sun, XK., Huo, HF. & Xiang, H. Bifurcation and stability analysis in predator–prey model with a stage-structure for predator. Nonlinear Dyn 58, 497–513 (2009). https://doi.org/10.1007/s11071-009-9495-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-009-9495-y

Keywords

Search

Navigation