Mathematical modelling of the effect of surface roughness on magnetic field profiles in type II superconductors

Abstract

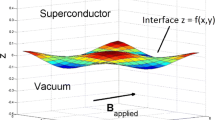
One of the defining characteristics of a superconductor is the Meissner effect, in which an external magnetic field is expelled from the bulk of a sample when cooled below the critical temperature. Although there has been considerable theoretical work on the Ginzburg–Landau theory of superconductors, the effects of interest in this paper can be modelled with the simpler London equation. This equation predicts an exponential decay of the local magnetic field magnitude as a function of the distance into the superconductor from a flat surface in the London limit where $\kappa =\lambda /\xi$, defined as the ratio between the penetration depth and coherence length, is much greater than 1. However, recent measurements of the field profile in high $\kappa$ superconductors show that the observed decay is non-exponential near the surface. In particular, the measured field profiles indicate that the decay rate in the field magnitude is smaller than expected from a simple London model on a short length scale $d$ near the surface. In this paper, we examine the effects of surface roughness on magnetic field penetration into a high $\kappa$ superconductor. We model the roughness as a sinusoidal perturbation from a flat interface and investigate the effect using both an asymptotic method, based upon a small-amplitude perturbation, and a numerical method, using a finite difference discretization with a coordinate mapping from an underlying rectangular domain. A novel discretization is used in the case of 3D calculations and a fast, preconditioned GMRES solver is developed. A careful comparison of asymptotic and numerical methods validates both approaches for small perturbations, but the numerical approach allows for the investigation of rougher surfaces. Our results show that surface roughness reduces the decay rate in the average magnetic field near the surface relative to a London model. However, the reduction is more gradual than the simple dead layer model currently being used to fit experimental data. In addition, we discover some interesting new phenomena in the 3D case.

Appendix

We define a parameter $N$ describing the number of points in the $x$- and $y$-directions and $M_m$ and $M_p$ describing how far the grid spans in the vacuum and superconducting sides respectively. Given $N\!,$ we proceed to define our spacings

$$\begin{aligned} h_x&= \frac{2 \pi }{N \omega _x},\end{aligned}$$

(104)

$$\begin{aligned} h_y&= \frac{2 \pi }{N \omega _y},\end{aligned}$$

(105)

$$\begin{aligned} h_\tau&= \min \{h_x, h_y\},\end{aligned}$$

(106)

$$\begin{aligned} h_I&= \frac{Mp}{N}; \end{aligned}$$

(107)

and our stretching parameters

$$\begin{aligned} \eta _v&= \frac{N h_\tau }{M_m},\end{aligned}$$

(108)

$$\begin{aligned} b_v&= \frac{\eta _v M_m + \frac{h_\tau }{2}}{\eta _v-1},\end{aligned}$$

(109)

$$\begin{aligned} a_v&= b_v + \frac{h_\tau }{2},\end{aligned}$$

(110)

$$\begin{aligned} \alpha _v&= a_v \log (M_m - b_v),\end{aligned}$$

(111)

$$\begin{aligned} \beta _v&= a_v \log \left( -\frac{h_\tau }{2} - b_v\right) ,\end{aligned}$$

(112)

$$\begin{aligned} \eta _s&= \frac{N h_\tau }{M_p},\end{aligned}$$

(113)

$$\begin{aligned} b_s&= \frac{\eta _s M_p + \frac{h_I}{2}}{\eta _s - 1},\end{aligned}$$

(114)

$$\begin{aligned} a_s&= -b_s,\end{aligned}$$

(115)

$$\begin{aligned} \alpha _s&= a_s \log (- b_s),\end{aligned}$$

(116)

$$\begin{aligned} \beta _s&= a_s \log (M_p -b_s). \end{aligned}$$

(117)

The careful selection of these $\alpha$ and $\beta$ parameters allows for the grids to interlock in the right way.

We set

$$\begin{aligned} \overline{x}_\mathrm{i}&= -\frac{\pi }{\omega _x} + (i-1) h_x \quad \text{ for } 1 \le i \le N,\end{aligned}$$

(118)

$$\begin{aligned} \overline{y}_j&= -\frac{\pi }{\omega _y} + (j-1) h_y \quad \text{ for } 1 \le j \le N,\end{aligned}$$

(119)

$$\begin{aligned} \underline{x}_\mathrm{i}&= \overline{x}_\mathrm{i} + \frac{h_x}{2},\end{aligned}$$

(120)

$$\begin{aligned} \underline{y}_j&= \overline{y}_j + \frac{h_y}{2}. \end{aligned}$$

(121)

We set

$$\begin{aligned} N_v = \left[ \frac{\beta _v - \alpha _v}{h_\tau }\right] +1 \end{aligned}$$

(122)

and

$$\begin{aligned} N_s = \left[ \frac{\beta _s - \alpha _s}{h_\tau }\right] +1, \end{aligned}$$

(123)

with $[ ]$ being the integer floor function, and define

$$\begin{aligned} {\underline{\tau }}_{N_v-k+1} = \beta _v - (k-1)h_\tau \quad \text{ for }\,k = 1,\ldots ,N_v \end{aligned}$$

(124)

and

$$\begin{aligned} {\overline{\tau }}_k = \alpha _s + (k-1)h_\tau \quad \text{ for }\,k=1,\ldots ,N_s. \end{aligned}$$

(125)

In the end we have $N^2 (N_v + 3 N_s)$ variables and equations to define. We define the mapping $K$ that takes an ordered $4$-tuple $(i, j, k, \ell )$ and maps them to a single number:

$$\begin{aligned} K(i,j,k,\ell ) = \left\{ \begin{array}{ll} (k-1)N^2 + (j-1)N + i &{} \text{ if } \ell = 0,\\ N^2 N_v + (\ell -1)N^2 N_s + (k-1)N^2 + (j-1)N + i &{} \text{ if } \ell \ne 0, \end{array} \right. \end{aligned}$$

(126)

where, to impose the periodic boundary conditions, $i$ and $j$ are taken mod $N.$

Based on this numbering, the $i,$ $j$ and $k$ describe the $x,$ $y$ and $\tau$ positions. The number $\ell = 0$ describes the $\tilde{g}$ variable (the variable in the vacuum including its ghost points), and $\ell = 1,2,3$ describes the first, second and third components of the magnetic field respectively in the superconducting coordinates.

To discretize $t,$ the depth past the surface, we define

$$\begin{aligned} t_{k} = \left\{ \begin{array}{lll} t_k = -\text{ e }^{(\underline{\tau }_k + \underline{\tau }_{k+1})/(2 a_v)} - b_v &{}\quad \text{ for } 1 \le k \le N_v-2,\\ t_{k} = \text{ e }^{(\overline{\tau }_{k+2-N_v})/a_s} + b_s &{}\quad \text{ for } N_v-1 \le k \le N_v + N_s - 3. \end{array}\right. \end{aligned}$$

(127)

For shorthand we define

$$\begin{aligned} \xi ^{(1)}&= \pm \omega _x \sin (\omega _x x) \cos (\omega _y y) a \text{ e }^{-\tau /a},\end{aligned}$$

(128)

$$\begin{aligned} \xi ^{(2)}&= \pm \omega _y \cos (\omega _x x) \sin (\omega _y y) a \text{ e }^{-\tau /a},\end{aligned}$$

(129)

$$\begin{aligned} \xi ^{(3)}&= \pm a \text{ e }^{-\tau /a},\end{aligned}$$

(130)

$$\begin{aligned} \xi ^{(4)}&= 2 \epsilon \xi ^{(1)},\end{aligned}$$

(131)

$$\begin{aligned} \xi ^{(5)}&= 2 \epsilon \xi ^{(2)}, \end{aligned}$$

(132)

$$\begin{aligned} \xi ^{(6)}&= \epsilon \left( \omega _x^2 + \omega _y^2\right) \omega _y^2 \cos (\omega _x x) \cos (\omega _y y)\left( \pm a \text{ e }^{-\tau /a}\right) \nonumber \\&\quad +\left( \epsilon ^2 \omega _x^2 \sin ^2(\omega _x x) \cos ^2(\omega _y y) + \epsilon ^2 \omega _y^2 \cos ^2 (\omega _x x) \sin ^2 (\omega _y y) + 1 \right) \left( -a \text{ e }^{-2 \tau /a}\right) , \end{aligned}$$

(133)

and

$$\begin{aligned} \xi ^{(7)} = \left( \epsilon ^2 \omega _x^2 \sin ^2 (\omega _x x) \cos ^2 (\omega _y y) + \epsilon ^2 \omega _y^2 \cos ^2(\omega _x x) \sin ^2(\omega _y y) + 1\right) \left( a^2 \text{ e }^{- 2 \tau /a}\right) , \end{aligned}$$

(134)

where $a = a_v$ in the vacuum and $a = a_s$ in the superconductor; the $-$ is chosen in the vacuum and the $+$ is chosen in the superconductor. These terms come from the coefficients of the Laplacian operator in $(x,y,\tau )$:

$$\begin{aligned} \bigtriangleup _{x,y,\tau } = \partial _{xx} + \partial _{yy} + \xi ^{(4)} \partial _{\tau x} + \xi ^{(5)} \partial _{\tau y} + \xi ^{(6)} \partial _{\tau } + \xi ^{(7)} \partial _{\tau \tau }. \end{aligned}$$

(135)

We discretize the $\xi$ variables with indices $(i,j,k,\ell ).$ For example,

$$\begin{aligned} \xi ^{(2)}_{i,j,k,0} = - \epsilon \omega _y \cos (\omega _x \underline{x}_\mathrm{i}) \sin (\omega _y \underline{y}_j) a_v \text{ e }^{-\underline{\tau }_k/a_v}. \end{aligned}$$

We use the notation

$$\begin{aligned} \xi ^{(m)}_{i,j,k \pm 1/2,\ell } = \frac{1}{2}\left( \xi ^{(m)}_{i,j,k \pm 1,\ell } + \xi ^{(m)}_{i,j,k,\ell }\right) . \end{aligned}$$

(136)

We can now present the discrete equations. We define $u$ as the unknown vector, $M$ as the matrix and $f$ as the load vector. The equations change based upon the $\tau$ position (index $k$), so in each slice the equations hold for all $i$ and $j.$

1.1 A.1 Conditions at $-\infty$

This corresponds to $k=1$ and $\ell = 0.$

We need to impose

$$\begin{aligned} \tilde{g}(x,y,-\infty ) = 0. \end{aligned}$$

To do so we set

$$\begin{aligned} f_{K(i,j,1,0)} = 0, \end{aligned}$$

(137)

with

$$\begin{aligned} M_{K(i,j,1,0),K(i,j,1,0)} = 1. \end{aligned}$$

(138)

1.2 A.2 Conditions at $-\infty$

This corresponds to $k=N_s$ and $\ell = 1,2,3.$

We need to impose

$$\begin{aligned} b_1(x,y,\infty ) = b_2(x,y,\infty ) = 0 \end{aligned}$$

and

$$\begin{aligned} \partial _z b_3(x, y, \infty ) = \xi ^{(3)} \partial _{\tau } b_3 = 0. \end{aligned}$$

This is an equation for the points with a $\overline{\tau }$ coordinate number $N_s.$ We impose

$$\begin{aligned} f_{K(i,j,N_s,\ell )} = 0. \end{aligned}$$

(139)

The point at $t = M_p$ is between regular grid and ghost points. We impose an average condition for the first two components (requiring their average to be zero) and a regular second-order derivative condition for the third component:

$$\begin{aligned}&M_{K(i,j,N_s,\ell ), K(i,j,N_s-1,\ell )} = \frac{1}{2},\end{aligned}$$

(140)

$$\begin{aligned}&M_{K(i,j,N_s,\ell ), K(i,j,N_s,\ell )} = \frac{1}{2}, \end{aligned}$$

(141)

for $\ell = 1,2,$ and

$$\begin{aligned}&M_{K(i,j,N_s,3), K(i,j,N_s-1,3)}= -\frac{1}{h_\tau } \xi ^{(3)}_{i,j,N_s,3},\end{aligned}$$

(142)

$$\begin{aligned}&M_{K(i,j,N_s,3), K(i,j,N_s,3)} = \frac{1}{h_\tau } \xi ^{(3)}_{i,j,N_s,3}. \end{aligned}$$

(143)

1.3 A.3 Vacuum Laplacian

Here, $k=2,\ldots ,N_v-1$ and $\ell = 0.$

The Laplacian is zero in the vacuum region, so

$$\begin{aligned} f_{K(i,j,k,0)} = 0. \end{aligned}$$

(144)

For the matrix entries we have

$$\begin{aligned}&M_{K(i,j,k,0),K(i\pm 1,j,k,0)} = \frac{1}{h_x^2},\end{aligned}$$

(145)

$$\begin{aligned}&M_{K(i,j,k,0),K(i,j\pm ,k,0)} = \frac{1}{h_y^2},\end{aligned}$$

(146)

$$\begin{aligned}&M_{K(i,j,k,0),K(i,j,k\pm 1,0)} = \frac{\pm \xi ^{(6)}_{i,j,k,0}}{2 h_\tau },\end{aligned}$$

(147)

$$\begin{aligned}&M_{K(i,j,k,0),K(i,j,k,0)} = -\frac{2}{h_x^2} - \frac{2}{h_y^2} - \frac{2 \xi ^{(7)}_{i,j,k,0}}{h_\tau ^2},\end{aligned}$$

(148)

$$\begin{aligned}&M_{K(i,j,k,0),K(i+1,j,k+1,0)} = \frac{\xi ^{(4)}_{i,j,k,0}}{4 h_x h_\tau },\end{aligned}$$

(149)

$$\begin{aligned}&M_{K(i,j,k,0),K(i-1,j,k-1,0)} = \frac{\xi ^{(4)}_{i,j,k,0}}{4 h_x h_\tau },\end{aligned}$$

(150)

$$\begin{aligned}&M_{K(i,j,k,0),K(i+1,j,k-1,0)} = \frac{-\xi ^{(4)}_{i,j,k,0}}{4 h_x h_\tau },\end{aligned}$$

(151)

$$\begin{aligned}&M_{K(i,j,k,0),K(i-1,j,k+1,0)} = \frac{-\xi ^{(4)}_{i,j,k,0}}{4 h_x h_\tau },\end{aligned}$$

(152)

$$\begin{aligned}&M_{K(i,j,k,0),K(i,j+1,k+1,0)} = \frac{\xi ^{(5)}_{i,j,k,0}}{4 h_y h_\tau },\end{aligned}$$

(153)

$$\begin{aligned}&M_{K(i,j,k,0),K(i,j-1,k-1,0)} = \frac{\xi ^{(5)}_{i,j,k,0}}{4 h_y h_\tau },\end{aligned}$$

(154)

$$\begin{aligned}&M_{K(i,j,k,0),K(i,j+1,k-1,0)} = \frac{-\xi ^{(5)}_{i,j,k,0}}{4 h_y h_\tau },\end{aligned}$$

(155)

$$\begin{aligned}&M_{K(i,j,k,0),K(i,j-1,k+1,0)} = \frac{-\xi ^{(5)}_{i,j,k,0}}{4 h_y h_\tau }. \end{aligned}$$

(156)

1.4 A.4 Superconductor Laplacian

Here, $k=2,...,N_s-1$ and $\ell =1,2,3.$

This is identical to the discretization of the vacuum Laplacian above except that the $0$ is replaced by $\ell = 1,2,3$ and the slight change in now having an extra $-1$ in these entries:

$$\begin{aligned} M_{K(i,j,k,\ell ),K(i,j,k,\ell )} = -\frac{2}{h_x^2} - \frac{2}{h_y^2} - \frac{2 \xi ^{(7)}_{i,j,k,\ell }}{h_\tau ^2} - 1. \end{aligned}$$

(157)

1.5 A.5 Zero divergence on interface

This is the scalar equation corresponding to the $\tilde{g}$ ghost points. We have $k=N_v$ and $\ell =0.$ We choose to impose zero divergence at the $\tilde{g}$ ghost points.

The divergence is zero, and we are looking at the equations for the vacuum ghost points. Therefore, we set

$$\begin{aligned} f_{K(i,j,N_v,0)} = 0. \end{aligned}$$

(158)

The entries of $M$ corresponding to the terms in $\partial _x b_1$ are shown below, and the other terms are similar. For the matrix $M,$ we impose

$$\begin{aligned}&M_{K(i,j,N_v,0), K(i,j,2,1)} = \frac{1}{4 h_x} + \frac{\xi ^{(1)}_{i,j,3/2,1}}{4 h_\tau },\end{aligned}$$

(159)

$$\begin{aligned}&M_{K(i,j,N_v,0), K(i,j,1,1)} = -\frac{1}{4 h_x} + \frac{\xi ^{(1)}_{i,j,3/2,1}}{4 h_\tau },\end{aligned}$$

(160)

$$\begin{aligned}&M_{K(i,j,N_v,0), K(i-1,j,2,1)} = \frac{1}{4 h_x} + \frac{\xi ^{(1)}_{i-1,j,3/2,1}}{4 h_\tau },\end{aligned}$$

(161)

$$\begin{aligned}&M_{K(i,j,N_v,0), K(i-1,j,1,1)} = -\frac{1}{4 h_x} + \frac{\xi ^{(1)}_{i-1,j,3/2,1}}{4 h_\tau },\end{aligned}$$

(162)

$$\begin{aligned}&M_{K(i,j,N_v,0), K(i,j-1,2,1)} = \frac{1}{4 h_x} + \frac{\xi ^{(1)}_{i,j-1,3/2,1}}{4 h_\tau },\end{aligned}$$

(163)

$$\begin{aligned}&M_{K(i,j,N_v,0), K(i,j-1,1,1)} = -\frac{1}{4 h_x} + \frac{\xi ^{(1)}_{i,j-1,3/2,1}}{4 h_\tau },\end{aligned}$$

(164)

$$\begin{aligned}&M_{K(i,j,N_v,0), K(i-1,j-1,2,1)} = \frac{1}{4 h_x} + \frac{\xi ^{(1)}_{i-1,j-1,3/2,1}}{4 h_\tau },\end{aligned}$$

(165)

$$\begin{aligned}&M_{K(i,j,N_v,0), K(i-1,j-1,1,1)} = -\frac{1}{4 h_x} + \frac{\xi ^{(1)}_{i-1,j-1,3/2,1}}{4 h_\tau }. \end{aligned}$$

(166)

1.6 A.6 Gradient condition

This corresponds to $k=1$ and $\ell =1,2,3.$

The condition is that

$$\begin{aligned} b = \nabla \tilde{g} + (1,0,0)^T \end{aligned}$$

or that

$$\begin{aligned} \nabla \tilde{g} - b = (-1,0,0)^T. \end{aligned}$$

These are equations for $b$ on the interface. Therefore, we set

$$\begin{aligned} f_{K(i,j,1,1)} = -1 \end{aligned}$$

(167)

and

$$\begin{aligned} f_{K(i,j,1,2)} = f_{K(i,j,1,3)} = 0. \end{aligned}$$

(168)

As with the divergence, we need to take averages in finding the derivatives. For an illustration, we show the equations for the third component of $b.$ They correspond to setting the entries of $M$ as follows:

$$\begin{aligned}&M_{K(i,j,1,3), K(i,j,N_v,3)} = \frac{\xi ^{(3)}_{i,j,N_v-1/2,0}}{4 h_\tau },\end{aligned}$$

(169)

$$\begin{aligned}&M_{K(i,j,1,3), K(i,j,N_v-1,3)} = \frac{-\xi ^{(3)}_{i,j,N_v-1/2,0}}{4 h_\tau },\end{aligned}$$

(170)

$$\begin{aligned}&M_{K(i,j,1,3), K(i-1,j,N_v,3)} = \frac{\xi ^{(3)}_{i-1,j,N_v-1/2,0}}{4 h_\tau },\end{aligned}$$

(171)

$$\begin{aligned}&M_{K(i,j,1,3), K(i-1,j,N_v-1,3)} = \frac{-\xi ^{(3)}_{i-1,j,N_v-1/2,0}}{4 h_\tau },\end{aligned}$$

(172)

$$\begin{aligned}&M_{K(i,j,1,3), K(i,j-1,N_v,3)} = \frac{\xi ^{(3)}_{i,j-1,N_v-1/2,0}}{4 h_\tau },\end{aligned}$$

(173)

$$\begin{aligned}&M_{K(i,j,1,3), K(i,j-1,N_v-1,3)} = \frac{-\xi ^{(3)}_{i,j-1,N_v-1/2,0}}{4 h_\tau },\end{aligned}$$

(174)

$$\begin{aligned}&M_{K(i,j,1,3), K(i-1,j-1,N_v,3)} = \frac{\xi ^{(3)}_{i-1,j-1,N_v-1/2,0}}{4 h_\tau },\end{aligned}$$

(175)

$$\begin{aligned}&M_{K(i,j,1,3), K(i-1,j-1,N_v-1,3)} = \frac{-\xi ^{(3)}_{i-1,j-1,N_v-1/2,0}}{4 h_\tau },\end{aligned}$$

(176)

$$\begin{aligned}&M_{K(i,j,1,3), K(i,j,1,3)} = -1. \end{aligned}$$

(177)

1.7 A.7 Finding the results

This averaging brings about a null vector for $M$ when $N$ is even. As a result, the program is restricted to odd values of $N$. This null vector is explained further in [9].

Given the system

$$\begin{aligned} Mu = f, \end{aligned}$$

we find

$$\begin{aligned} u = M^{-1}f. \end{aligned}$$

This gives a magnetic field on the superconducting side, but only gives $\tilde{g}$ on the vacuum side. To get $b$ on the vacuum side, we take the discretized gradient of $\tilde{g}$ just as was done previously, thereby finding the magnetic field at values at the centres of cubes with $\tilde{g}$ values. We also add $1$ to the first component.