Toward the development of a feature-space representation for a complex natural category domain

Abstract

This article reports data sets aimed at the development of a detailed feature-space representation for a complex natural category domain, namely 30 common subtypes of the categories of igneous, metamorphic, and sedimentary rocks. We conducted web searches to develop a library of 12 tokens each of the 30 subtypes, for a total of 360 rock pictures. In one study, subjects provided ratings along a set of 18 hypothesized primary dimensions involving visual characteristics of the rocks. In other studies, subjects provided similarity judgments among pairs of the rock tokens. Analyses are reported to validate the regularity and information value of the dimension ratings. In addition, analyses are reported that derive psychological scaling solutions from the similarity-ratings data and that interrelate the derived dimensions of the scaling solutions with the directly rated dimensions of the rocks. The stimulus set and various forms of ratings data, as well as the psychological scaling solutions, are made available on an online website (https://osf.io/w64fv/) associated with the article. The study provides a fundamental data set that should be of value for a wide variety of research purposes, including: (1) probing the statistical and psychological structure of a complex natural category domain, (2) testing models of similarity judgment, and (3) developing a feature-space representation that can be used in combination with formal models of category learning to predict classification performance in this complex natural category domain.

A ubiquitous component of science education is learning the key categories of the target domain. For example, botanists are expert at identifying different types of plants; entomologists at insect identification; and geologists at identifying and classifying rocks. A long-term goal of the present project is to apply principles of category learning gleaned from the field of cognitive psychology to help guide the search for effective techniques of teaching categories in the science classroom. Our specific example target domain is the teaching of rock identification and classification in the geologic sciences. Learning such classifications is one of the primary early goals in geology courses in both the classroom and the field: Determining the rock categories that compose a given terrain is a first step in allowing the geologist to move toward his or her ultimate goal of making inferences about the geologic history of that terrain.

There is an enormous variety of different techniques that might be used for the teaching of scientific classifications. For example, among the fundamental questions addressed in the cognitive psychology of category learning are: (i) Which training instances should be used? (ii) In what order should the instances be presented? (iii) What mixings of study versus testing should be applied? And (iv) Should the focus be on teaching general rules or learning by induction over examples?

Conducting empirical studies to systematically navigate through the vast set of combinations of teaching possibilities would be an extraordinarily time-consuming process. Lindsey, Mozer, Huggins, and Pashler (2013) proposed techniques that are analogous to conducting “parameter searches” through alternative empirically tested designs to locate optimal instruction policies. We propose a complementary idea, namely that to conduct a more efficient search, one might use successful models of human category learning to simulate the outcome of different teaching techniques (e.g., Patil, Zhu, Kopec, & Love, 2014). One could then focus empirical studies on those techniques that the models predict would be most successful.

Application of such formal models of category learning, however, requires the specification of a multidimensional feature space in which the to-be-classified objects are embedded (Ashby, 1992; Nosofsky, 1986, 1992). The primary goal of the research reported in the present article is to make in-roads into the goal of developing a detailed feature-space representation for the natural category domain of rock types, which would ultimately serve as the foundation for the application of the formal models of classification.

In highly controlled laboratory experiments for testing models of classification, researchers generally use simple perceptual stimuli varying along a small number of dimensions. Examples include shapes varying in size and angle; colors varying in brightness and saturation; or schematic faces varying along manipulated dimensions such as eye separation, mouth height, and so forth (for a review, see Nosofsky, 1992). In such domains, well-known similarity-scaling techniques, such as multidimensional scaling, tree-fitting or additive clustering, can be used to precisely measure the similarities among objects and develop a feature-space representation for them (Shepard, 1980). In such techniques, varieties of similarity data are collected, and a feature-space representation is derived that provides a good quantitative account of the observed similarity data.

In a real-world natural category domain such as rocks, however, the derivation of a feature-space representation becomes a highly ambitious task, and there is a wide variety of reasons why traditional similarity-scaling techniques may prove to be inadequate if used on their own. One reason is that certain dimensions that may be crucial for making fine-grained distinctions between different categories of rocks may be ignored in the context of a generic similarity-judgment task. If so, then such dimensions would not appear in the derived feature-space representation, and the models of human category learning that rely on such a representation would be severely handicapped. A second reason is that natural objects such as rocks are composed of a very large number of complex dimensions. Similarity-scaling techniques may be limited in their power to reliably extract all dimensions, even if observers do make use of them in judging similarities. A third reason is a practical one: In the rock-category domain that we investigate, there are hundreds of to-be-classified instances. Traditional similarity-scaling techniques involve the construction and analysis of n x n matrices of data (where n is the number of objects). When n is large, the amount of data collection that is required for filling out such matrices is prohibitive.¹

Therefore, one of our main ideas in the present research is to pursue, along with similarity-scaling methods, a complementary method for constructing the feature-space representation -- namely by collecting direct dimension ratings for the large set of rock stimuli. For example, based on characterizations provided in college-level geology textbooks (e.g., Marshak, 2013; Tarbuck & Lutgens, 2015), as well as on preliminary similarity-scaling work with these stimuli that we have already conducted (Nosofsky et al., 2016), some salient dimensions of the rock stimuli include darkness/lightness of color, average grain size, and the extent to which the composition of the rock is organized or disorganized. Because observers appear to have reasonably direct access to such dimensions, a straightforward approach to developing a feature-space representation is to have participants provide direct ratings of the rocks along each of these dimensions. One of the central goals of the present project is develop a data set that provides detailed ratings along a large number of candidate dimensions for a large library of rock instances.

There are examples of successful applications of such methods in past research involving the classification of high-dimensional perceptual stimuli. To take one example, Getty, Swets and their colleagues pursued techniques for improving the ability of medical practitioners to make diagnostic decisions in domains such as mammography (Getty, Pickett, D’Orsi, & Swets, 1988; Swets, Getty, Pickett, et al., 1991). With the goal of discriminating between the classes of benign versus malignant breast tumors, expert judges provided ratings of training instances of the tumors along a list of candidate dimensions, such as the nature of the tumors’ borders (smooth vs. irregular), whether the tumor seemed to be invading neighboring tissue, and so forth. Given the configuration of the rated training instances in the dimensional space, the researchers then computed the optimal linear discriminant function for separating the benign versus malignant classes. Participant practitioners were then provided with novel test cases. They provided ratings of the novel cases on the same list of dimensions as for the original training instances. The computerized linear-discriminant classifier could then be used to predict the probability that each test case belonged to the benign versus malignant categories. A variety of studies demonstrated that the expert practitioners could improve their classification performance if they supplemented their own judgments with the recommendations provided by the computer classifier.

Although this medical-diagnosis example suggests that the use of direct dimension ratings can have major practical benefits, the proposed technique is not without its own potential limitations. First, the response function that is involved in the translation of psychological scale values onto the direct ratings is unknown. Second, the manner in which values along separate dimensions interact needs to be specified. Third, not all dimensions that enter into participants’ perceptions of the stimuli may be easily accessible. Indeed, the reason why similarity-scaling techniques are so valuable is to overcome these kinds of shortcomings. Finally, whereas the target domain addressed by Getty, Swets and their colleagues in the medical-diagnosis example involved discriminating between two broad categories of perceptual objects (radiographs of benign vs. malignant tumors), our target goal is the teaching of 30 classes, many of which appear to involve highly subtle distinctions (see below).

Accordingly, the approach that we envision for developing an adequate feature-space representation for the rock stimuli is one that combines elements of the direct dimension-ratings and similarity-scaling methods. Therefore, in the present research, in addition to collecting an extensive set of direct dimension-ratings data, we also conduct a variety of similarity-scaling studies involving the rock stimuli. As will be seen, these combined methodological approaches will prove to be highly complementary, with each informing the other.

Overview of studies

We compiled a set of 360 pictures of rocks. There were ten common subtypes from each of the broad categories igneous, metamorphic, and sedimentary (30 subtypes total). The subtypes are listed in Table 1. There were 12 tokens of each of these 30 subtypes.

Table 1 Subtypes of igneous, metamorphic, and sedimentary rocks used in the dimension-ratings and similarity-judgment experiments

In a direct dimension-ratings study, subjects provided ratings for all 360 rocks along a set of 18 candidate dimensions (see Method section for a detailed listing of the dimensions). In one similarity-judgment study, we selected a single representative token of each of the 30 subtypes, and subjects provided similarity judgments among all pairs of these 30 representative tokens.² The goal of this study was to produce high-precision pairwise similarity-judgment data for a representative subset of the rock instances. In a second similarity-judgment study, each individual subject provided similarity judgments for randomly chosen tokens from among all 360 rock instances. This method produced an extremely large matrix of pairwise similarity judgments, but with the matrix being extremely sparse in terms of number of data observations at the individual-cell level. (There are 129,600 cells in a 360 x 360 matrix.) Although the average number of data entries in each individual cell is extremely small, there is nevertheless a great deal of redundancy in the matrix, because each row provides information regarding the similarity of a single rock token to all other 359 tokens. It is an open question whether similarity-scaling analyses of such a matrix will recover structured representations for the stimulus domain under investigation.

One of the major purposes of the present article is simply to report the collected data from our dimension-ratings and similarity-judgment studies and make them available to the international research community. Accordingly, we have developed an online website associated with the article (https://osf.io/w64fv/) that provides the stimulus materials and obtained data.

We believe that the data-collection process initiated in the present study will ultimately be extremely useful for a wide variety of purposes, including: (i) providing a bedrock feature space for the testing of alternative models of classification learning in a real-world natural-science category domain; (ii) attempts to characterize in some detail the dimensional structure of that domain; (iii) the testing of alternative theoretical models of similarity judgment; and (iv) providing information of value for education and teaching in the geological sciences. We elaborate on these various potential uses in the context of reporting our data. In addition, we initiate some of these uses in the present article by conducting theoretical analyses that inter-relate the dimension ratings and similarity-judgment data.

Method

Subjects

The subjects in the direct dimension-ratings study were 60 members of the Indiana University community (mostly graduate students) who were paid $12 per each one-hour session. Each subject participated in four 1-hour sessions. (Each main dimension-rating condition took a single 1-hour session to complete, whereas a color-matching condition took two hours to complete.) The subjects in the similarity-judgment studies were 356 undergraduates from Indiana University who participated in partial fulfillment of an introductory psychology course requirement. There were 82 subjects in similarity-judgment Study 1 and 274 subjects in similarity-judgment Study 2. All subjects had normal or corrected-to-normal vision and all claimed to have normal color vision. All subjects were naïve with respect to the domain of rock classification. We envision future studies in which experts in the domain provide analogous forms of data.

Stimuli

The stimuli were 360 pictures of rocks. We obtained the pictures from web searches, and used photo-shopping procedures to remove background objects and idiosyncratic markings such as text labels. There were ten subtypes from each of the main categories igneous, metamorphic, and sedimentary (30 subtypes total; see Table 1), and 12 tokens of each of the 30 subtypes. The complete set of rock images is available in the “Rocks Library” folder in the article’s website.

The stimuli were presented on a 23-in. LCD computer screen. The stimuli were displayed on a white background. Each rock picture was approximately 2.1 in. wide and 1.7 in. tall. Subjects sat approximately 20 in. from the computer screen, so each rock picture subtended a visual angle of approximately 6.0° x 4.9°. Images were selected or digitally manipulated to have similar levels of resolution of the salient features that may be used to identify and classify the particular rock types. All of the images were photographed in a field setting and had not been modified in any way other than the removal of other portions of the original image. The experiments were programmed in MATLAB and the Psychophysics Toolbox (Brainard, 1997).

Procedure

Dimension-ratings study

Subjects provided direct dimension ratings in 11 main conditions, including a color-matching condition. (As explained in more detail below, in some conditions, multiple dimensions were rated.) The rated dimensions are listed in Table 2. Our choice of candidate dimensions was motivated by descriptions of rock categories provided in college-level geology textbooks (e.g., Marshak, 2013; Tarbuck & Lutgens, 2015) and by results from preliminary similarity-scaling analyses of the Study-1 similarity-judgment data reported in another article (Nosofsky et al., 2016). In our view, our list of candidate dimensions makes significant headway into providing a first-order feature-space characterization for the rock pictures, but there is no reason why future studies cannot expand the list to develop a more complete characterization. Also, as explained in more detail below, in addition to the ratings of the visual aspects of the rock pictures, the article’s website provides information concerning characteristics of the rocks along certain non-visual dimensions, such as results from various mechanical and chemical testing procedures.

Table 2 Listing of rated dimensions in the direct dimension-ratings experiment

In all conditions, on each trial, a single picture from the 360-picture set was presented at the center of the computer screen and subjects provided a rating for the rock that was appropriate to the condition in which they were being tested. In all conditions, the order in which the pictures were presented was randomized for each individual subject.

We denote Dimensions 1–6 in Table 2 as “continuous” dimensions. For these dimensions, subjects provided a rating for the rock pictures on a 1-9 scale. For example, in the “lightness of color” condition, subjects were instructed to provide a rating of 1 for the very darkest rocks, a rating of 9 for the very lightest rocks, and a rating of 5 for rocks of average darkness/lightness. In an attempt to promote the use of consistent scale values across subjects, anchor pictures were displayed along with scale values on the computer screen throughout each rating session. One anchor picture corresponded to the lowest rating (e.g, the very darkest rock), a second anchor picture corresponded to the highest rating (e.g, the very lightest rock), and a third anchor corresponded to a rock that we judged to be roughly average on the rated dimension (e.g., a rock of average darkness/lightness). The anchors and scale values were displayed at the bottom of the screen throughout the rating session (see Fig. 1 for an example screen shot). Note that the extreme anchor pictures were displayed midway between the 1–2 and 8–9 scale values to provide subjects with some flexibility in assigning their ratings. For example, if a subject judged that our darkest anchor rock was not as dark as some others, then he or she could assign it a rating of 2 and the other rocks a rating of 1. Subjects were instructed to try to use the full range of scale values in making their ratings.

Fig. 1

Example screen display on a trial of the dimension-ratings experiment

We denote Dimensions 7–12 as “present-absent” dimensions. Although these dimensions can also be viewed as varying in continuous fashion, it seemed to us to be more natural and efficient to ask for “present-absent” judgments on such dimensions. One example of a present-absent dimension was whether or not a rock contained holes. In various cases, if subjects provided a “present” rating on such dimensions, then they also provided a continuous rating regarding the nature of that present dimension (Dimensions 13–15 of Table 2). We denote these latter dimensions as “conditional continuous” dimensions. For example, if a subject judged that a rock had stripes or bands (“present”), then they provided a continuous rating on a scale from 1–9 of the extent to which the stripes were straight (1) versus curved (9). In these cases, a subject would press the “N” key on the computer keyboard if they judged that the feature was not present; whereas they would press one of the keys 1–9 to both indicate that the feature was present and to describe the nature of that present feature. For example, in the stripes condition, subjects would press the “N” key if they judged that the rock had no stripes; the “1” key for rocks that had the straightest stripes; the “5” key for rocks that had stripes of average straightness/curviness; and the “9” key for rocks that had stripes that were the most curved. Again, anchor pictures were displayed at the bottom of the screen to provide examples of the requested ratings. The combinations of present/absent and conditional-continuous dimensions were: stripes (straight/curved), fragments (angular/rounded), and presence of a visible grain (variability of size of grain). Each of these combinations of present/absent and “conditional-continuous” dimensions was rated in a separate main condition of testing. We did not collect conditional-continuous ratings on the present/absent dimensions “holes”, “physical layers”, or “other salient special feature”. Instead, within a single main condition, subjects pressed the “1” key if they judged that a rock had holes; the “2” key if they judged it was composed of physical layers; the “3” key if they judged that some other highly salient special feature was present (e.g, the presence of a fossil); and the “N” key if none of these features was present. Because extremely few (if any) rocks had combinations of these relatively rare features (see Appendix Table 7), the response constraint that only a single such feature could be indicated had negligible effects on the data-collection process.

Another condition that was tested as part of the dimension-ratings experiment was a color-matching condition. In this condition, a set of 96 color squares was displayed simultaneously on the computer screen. Each color square was .375 in. in width and height. The squares were arranged in rows, and adjacent squares in each row were separated by .375 in.

Each of 87 of the 96 color squares closely matched one of 87 Munsell color chips provided in the Munsell Geological Rock Color Chart (1991).³ In addition, a set of nine achromatic color squares (equal values on the R, G, and B coordinates) was displayed. The achromatic colors varied only in lightness; the first 8 ranged from dark black (RGB = [0, 0, 0]) to off-white (RGB = [224 224 224]) in equal RGB steps, with the ninth and whitest square set at RGB = [240 240 240]. The color squares were arranged in rows on the computer screen in approximate color families. For example, the top row contained colors in the red and orange family; the second row contained colors in the yellow and light green family; and so forth. (The bottom row contained the achromatic color squares.)

On each trial, a single rock picture was displayed at the top of the computer screen. Subjects were instructed to use the computer mouse to click on the color square that most closely matched the dominant color of the rock. The Munsell value (brightness), chroma (saturation) and hue associated with the color square chosen on each trial were recorded.

Three separate groups of 20 subjects each provided dimension ratings across the various conditions. One group provided ratings of lightness of color, average grain size, variability of grain size (conditional on the judged presence of a visible grain), and smoothness/roughness. A second group provided ratings of shininess, organization, angular versus rounded fragments (conditional on the judged presence of fragments), and straight versus curved bands (conditional on the judged presence of bands). A third group provided ratings of color variability; presence versus absence of holes, physical layers, or other special features; and color-matching judgments. The order of conditions within each group was roughly balanced across subjects.⁴

Rocks-30 similarity-judgment study

In this study, guided by the advice of the expert geology educator on our team (our fourth author), we selected a single rock token from each of the 30 subtypes that was representative of the subtype as a whole. The selected tokens are reported in the “Rocks-30 Similarity-Judgment” folder of the article’s website. Subjects provided similarity judgments on a scale from 1 (most dissimilar) through 9 (most similar) for each of the 435 unique pairs of these 30 tokens. The members of the pair of stimuli presented on each trial were horizontally centered around the central location on the screen and were separated by approximately 3.5 in. The ordering of the pairs was randomized for each subject, as was the left-right placement on the computer screen of the members of each pair on each trial. Subjects were instructed to try to use the full range of scale values in making their ratings. No instructions were provided regarding the basis for the similarity judgments: Subjects based their judgments on whatever aspects of the rock pictures they deemed appropriate.

Rocks-360 similarity-judgment study

In this study, similarity judgments were collected for all 360 rock tokens. Again, each subject provided similarity judgments for all 435 unique pairs of the 30 subtypes. However, whereas in the rocks-30 study there was only a single representative token of each subtype, in this rocks-360 study we randomly sampled the tokens from each subtype on each trial. In addition, subjects provided similarity judgments for within-subtype token pairs. For example, on a given trial, a subject might judge the similarity between two randomly selected tokens from Subtype 1. (The sampling was constrained, however, such that the within-subtype tokens were always distinct from one another.) Participants were presented with one random pair from within each of the 30 subtypes. Thus, each subject provided a total of 465 similarity judgments: 435 between-subtype ratings and 30 within-subtype ratings. All other aspects of rocks-360 similarity-judgment study were the same as for the rocks-30 study.

Results

Dimension-ratings data

Report of the basic data

The individual-subject data obtained in the dimensions-rating experiment are provided in the “Dimension Ratings” folder of the article’s website.

In an initial analysis, we computed averaged ratings (and the standard deviation of ratings) for each of the 360 rock stimuli along each of the dimensions. These averages and standard deviations, which will be used in various subsequent analyses reported in this article, are also provided in the website’s “Dimension Ratings” folder. For continuous dimensions 1–6, we simply computed the averaged ratings across all subjects on the 1–9 rating scale. For present-absent dimensions 7–12, the values are the proportions of subjects who judged each feature to be present in each rock.

For conditional-continuous dimensions 13–15, we first computed the averaged ratings given that a subject judged the feature to be present in the rock in the first place. Note that in many cases, these conditional averages might be based on ratings from very few subjects, because most subjects might have judged that the feature was not present in the rock. Our strong intuition was that a conditional rating based on a very small sample size of “present” judgments does not provide the same magnitude of evidence as the same averaged rating based on a large sample size of “present” judgments. For example, suppose that only a single subject judged that rock i had stripes and that the subject’s stripe-curvature rating for rock i was 9; whereas all 20 subjects might have judged that rock j had stripes, with the averaged curvature rating also being 9. Our intuition is that the evidence for curvature in stripes is far greater for rock j than for rock i. To capture this intuition, we computed the following transformed rating (R’) of the averaged conditional-continuous dimension ratings (R):

$$ {R}^{\hbox{'}}=\rho \left( R-5\right)+5 $$

(1)

where p is the proportion of subjects who judged that the present-absent feature was present in the rock. This transformation squeezes the averaged ratings towards the neutral value of 5 in cases in which only a small proportion of subjects judged the feature to be present. By comparison, the transformed value is the same as the original value in cases in which all subjects judged the feature to be present.

The averaged values on the dimensions derived from the color-matching condition were computed as follows. First, as explained previously, according to the Munsell (1946) system, each color square had an associated lightness (“Value”), saturation (“Chroma”), and Hue. For each rock, the averaged values of lightness and saturation were simply the averages (computed across the 20 subjects) of the Value (V) and Chroma (C) values associated with the selected color squares for that rock.

Producing average values of “Hue” is more complicated, for two reasons. First, hue is a circular dimension. Second, the ability to discriminate hues varies with the saturation of the colors: as hues become less saturated, it becomes more difficult to discriminate among them (e.g., Landa & Fairchild, 2005).

Thus, to produce sensible averaged ratings, we conducted the following transforms. First, there were 40 hues spanning the complete Munsell color circle ranging from 2.5 Red to 10 Red-Purple. Following the assumptions in the Munsell (1946) system, we presumed that these 40 hues were evenly spaced around the 360° color circle. Thus, each successive hue is associated with an equally spaced angle on the color circle. Second, for each rock, the hue angle chosen by a given subject was transformed to x-y coordinates on the unit circle. Third, using cylindrical coordinates (e.g., Moon & Spencer, 1988), these x and y values were transformed using the transform

$$ \begin{array}{l} x'= C'* x\\ {} y' = C'* y\end{array} $$

where C denotes chroma and C’ = C/10. Thus, hues that are very low in saturation produce x’-y’ values near (0,0), the defined x-y hue values for the achromatic colors black/gray/white. This transformation captures the fact that the hues of colors that are low in saturation are difficult to discriminate. Finally, the averaged hue values for each rock are simply the averages (computed across the 20 subjects) of the transformed x’ and y’ values defined above. Note that it is the pairs of x’-y’ values just described that define each hue: the individual values of x’ and y’ are not psychologically meaningful in isolation. Any rigid rotation of the x’-y’ values around the origin produces equivalent psychological distances among the hues, and where the distance of the x’-y’ point from the origin is proportional to the Chroma value for the color.

Examination of the dimension ratings

As discussed in our introduction, a key question that we begin to address in this article is the extent to which the dimension ratings can be used to make successful predictions of performance in independent tasks. Before turning to this issue, however, we first report here various preliminary analyses that we have conducted that suggest that the dimension ratings are psychologically meaningful and have a good deal of internal consistency. For example, in one analysis, we computed correlations between the averaged ratings of the 360 rocks across all pairs of dimensions (with the exception of the circular dimension of hue). The complete correlation matrix is provided in the “Dimensions Ratings” folder on the article’s website. In the vast majority of cases, the correlations between the dimension ratings were low in magnitude, as would be expected if the dimensions are describing nearly independent characteristics of the rocks. However, in a subset of cases, we observed very high inter-dimensional correlations (|r| > .75); it turns out that, in all these latter cases, the finding of the high correlations seems highly sensible. For example, note that our procedures allowed us to derive two separate estimates of the darkness/lightness of each rock. One procedure involved direct dimension ratings of darkness/lightness, whereas the second involved the derivation of lightness values through our color-matching condition. The correlation between the darkness/lightness ratings obtained from these two procedures was r=.95. All other dimension pairs that yielded high correlations (|r|> .75) are listed in Table 3. For example, there was a high correlation between average grain size and presence of fragments: This result is sensible because rocks that are composed of fragments that are readily identified in a hand specimen are precisely those that will tend to have the coarsest grain size. Likewise, there was a high correlation between average grain size and roughness of texture: The presence of coarse-grained fragments or large crystals is likely to produce rough textures, especially when the components are exposed to weathering. In a nutshell, although the dimensions listed in Table 3 refer to conceptually distinct aspects of the rocks, the fact that their values are highly correlated seems sensible and suggests that the dimensions-ratings data are regular and systematic.

Table 3 Listing of pairs of dimensions with high correlations (|r| > .75)

In a second approach to probing the dimension-ratings data, we examined the patterns of ratings for three selected pairs of subtypes of rocks: obsidian-anthracite, breccia-conglomerate, and diorite-granite. Representative tokens of these three pairs are illustrated in Fig. 2. As will be seen, the results from the Rocks-360 similarity-judgment study that we report later in this article indicated that within each of these pairs, the members of the two subtypes were highly similar to one another. Thus, we hypothesized that each pair of selected rock subtypes would have highly similar values along most of their rated dimensions. At the same time, the Rocks-360 similarity-judgment study indicated that the selected subtypes belonging to different pairs were very dissimilar; thus, we hypothesized that we would see dramatic differences in numerous dimension ratings across the different sets of pairs.

Fig. 2

Representative tokens of selected pairs of subtypes with high within-pair similarity and low between-pair similarity. Top panel: obsidian (left) versus anthracite (right); middle panel: breccia (left) versus conglomerate (right); bottom panel: granite (left) versus diorite (right)

In the following analyses, for each pair, we compute the averaged dimension ratings across the 12 tokens that compose each subtype and simply plot these averaged ratings for inspection.⁵ To facilitate the visual presentation and ease of inspection of the ratings, we placed the “presence-absence” mean probability values (Dimensions 7–12) on roughly the same scale as the continuous dimensions by multiplying the presence-absence probabilities by 10. The results of our focused comparisons are displayed in the panels of Fig. 3.

Fig. 3

Mean dimension ratings, averaged across all subjects and tokens, for the three selected pairs of rock subtypes illustrated in Fig. 2. Top panel: obsidian (circles) vs. anthracite (crosses); middle panel: breccia (circles) versus conglomerate (crosses); bottom panel: granite (circles) versus diorite (crosses). Dimension descriptions corresponding to each dimension number are provided in Table 2. Points marked with a large-black dot or large-size cross show dimensions that we hypothesized would have larger-magnitude differences than the remaining dimensions

First, consider the pair obsidian-anthracite (for examples, see top panel of Fig. 2). Both are dark black, shiny rocks with little or no visible grains. Perhaps the main visual dimension that distinguishes between them is smoothness/roughness: Geology texts describe obsidian as having a glassy texture. Furthermore, when obsidian breaks or fractures, it often results in a gradual and smoothly curving breakage surface termed “conchoidal fracture.” By contrast, anthracite tends to have a rougher texture. Another distinguishing feature is that, although not always easily visible, anthracite is composed of compressed layers originating during deposition as well as fractures that develop during metamorphism. Thus, our hypothesis was that obsidian and anthracite would show similar ratings across all dimensions except smoothness/roughness (Dimension 3; D3) and presence of physical layers (D11). The mean ratings for obsidian and anthracite along the 17 rated dimensions (excluding the circular dimension of hue) are displayed in the top panel of Fig. 3. As expected, both subtypes are rated as shiny, very dark, and with little or no visible grain. In accord with our hypotheses, the main dimensions along which they differ (indicated by the enlarged, bold symbol markings) are indeed the dimensions of smoothness/roughness (D3) and presence of physical layers (D11).⁶

Our second focused comparison is breccia versus conglomerate – representative examples are shown in the middle panel of Fig. 2. Both are sedimentary rocks composed of fragments that are cemented together in haphazard fashion. We expected that both subtypes would have very high ratings on dimensions such as “average grain size” (D2), “visible grain” (D7), and “presence of fragments” (D8). Furthermore, due to the haphazardly cemented-together fragments, both subtypes generally have rough textures (D3) and high color variability (D6), while being low in regularity or organization (D5). The key dimension that distinguishes between breccia and conglomerate is that the former is composed of angular fragments, whereas the latter is composed of rounded fragments (D14). Thus, we hypothesized that the ratings for breccia and conglomerate would differ primarily on D14. As can be seen from inspection of the middle panel of Fig. 3, all of our above-stated hypotheses regarding the breccia-conglomerate comparison were confirmed.

Finally, we compare granite and diorite – for examples, see the bottom panel of Fig. 2. Both are coarse-grained igneous rocks with a mix of light and dark grains. Although there are exceptions, the grain tends to be far more homogeneous and organized than are the patterns of cemented-together fragments found in breccia and conglomerate. Neither type of rock has salient distinctive features such as holes or physical layers. Although diorite tends to be slightly darker, on average, than is granite, the distinction is often quite subtle, and was not clearly evident in the particular samples from our rocks library. Geology texts list a subtle secondary feature, not included in our ratings, for discriminating between granite and diorite, namely the presence of quartz crystals in the former but not the latter. Another potential discriminating cue is that whereas diorite is almost always achromatic (mixes of whites, grays, and black), some types of granite may be pink, red, or orange. Thus, our hypothesis was that the ratings for granite and diorite would be nearly identical across all the dimensions included in our task, with the exceptions that: i) granite might have slightly higher ratings of lightness of color than diorite (D2), and ii) the averaged chromaticity ratings for granite would be somewhat higher than for diorite (D17). As shown in the bottom panel of Fig. 3, granite did indeed receive higher average ratings of chromaticity than did diorite, although the hypothesis that it would also be rated as lighter in color (on average) than diorite was not supported. As expected, the two subtypes received extremely similar ratings on all remaining dimensions.

Additional information involving the dimension-ratings data

The analyses depicted in Fig. 3 involved focused comparisons among only three pairs of rock subtypes for the purpose of providing evidence of the systematic nature of the dimension-ratings data. A more complete data summary is provided in the appendix, which provides tables of the means and standard deviations of ratings of all 30 subtypes along each of the 17 dimensions. (These tables are also available in an interactive electronic format in the “Dimension Ratings” folder of the article’s website.) Although a full discussion goes beyond the scope of this article, the information provided in these tables should be very useful to investigators who wish to use the pictures of the rock subtypes for various purposes in behavioral-research experiments. For example, suppose one wishes to select experimental stimuli that differ substantially in lightness versus darkness of color: Inspection of the mean ratings (see Appendix Table 7) on Dimension 1 (lightness/darkness) provides immediate information that pumice, marble and rock gypsum are all very light-colored subtypes, whereas obsidian, amphibolite, and anthracite are all very dark colored. The table also provides indications of what are likely to be significant challenges in the learning of rock classifications. For example, inspection of the table reveals that, despite both being igneous rocks, pumice and obsidian differ by substantial magnitudes on numerous dimensions; whereas obsidian and anthracite, despite belonging to different high-level categories, have very similar values on almost all the dimensions (see also Fig. 3). We reprise these issues involving the structure of the high-level rock categories in our General discussion.

The standard deviations of the subtype-summary ratings (see Appendix Table 8) are computed using tokens as the unit of analysis – thus, the standard deviations provide a measure of the extent to which the tokens within a subtype vary from one another on each dimension. Inspection of the table reveals, for example, that rhyolite has high variability along a number of the dimensions, including lightness/darkness (D1); color variability (D6); presence of fragments (D8), bands (D9), and holes (D10); straightness/curviness of bands (D15); and Munsell brightness (D16). Interestingly, as will be seen in our subsequent report of the Rocks-360 similarity-judgment data, the within-category similarity judgments among the tokens of rhyolite were among the lowest of any subtype. Such results provide initial evidence of important connections between the direct dimension-ratings data and the similarity-judgment data, and we pursue this theme more systematically in the forthcoming sections of our article.

Summary

This section of our article provided information concerning the manner in which the dimension-ratings results were computed and provided a detailed report of the data. It also provided preliminary evidence that the dimension-ratings data are regular and systematic and accurately reflect some major properties of the rocks. A further form of such evidence will be provided in analyses in the next section that formally inter-relate the results from the dimension-ratings data with the similarity-judgment data.

Rocks-30 similarity-judgment study

The individual-subject data from the Rocks-30 Similarity Judgment Study are provided in the “Rocks-30 Similarity Judgment Study” folder of the article’s website. We computed the correlation between each individual subject’s 435 similarity judgments and the 435 judgments in the averaged similarity-judgment matrix. After inspecting a histogram of these correlations, we decided to delete as outliers the data of 11 of the subjects with correlations less than r=.30.⁷ (The data files of the deleted subjects are indicated in the actual file names in the website folder.) The averaged similarity-judgment data from the remaining 71 subjects are also reported in the website folder.

Rocks-360 similarity-judgment study

The individual-subject data from the Rocks-360 Similarity Judgment Study are provided in the “Rocks-360 Similarity Judgment Study” folder of the article’s website. These data files indicate not only the subtype-pair presented on each trial, but the particular randomly selected tokens within each subtype that were presented. Although the Rocks-360 study provides information regarding the similarities between the 360 individual tokens, we started the analysis by computing a collapsed 30 x 30 “subtype-similarity” matrix. Specifically, the entry in cell i-j of the collapsed matrix was the average (computed across all subjects) of the similarity ratings between the randomly selected tokens from subtypes i and j. This collapsed matrix also included the 30 self-similarity cells in which subjects rated the similarity of distinct tokens belonging to the same subtype. We computed the correlation between each individual subject’s 465 similarity judgments and the 465 entries in the collapsed matrix. For this study, based on our inspection of the resulting histogram of correlations, we decided to delete as outliers the data of 21 subjects with correlations less than r=.20. Along with the individual-subject data, the collapsed mean-similarity judgment matrix (and a matrix of standard deviations of collapsed judgments) is provided in the “Rocks-360 Similarity Judgment Study” folder of the website.

Analysis of data from the rocks-30 similarity-judgment study

There is an extremely wide variety of different models that one might use to analyze the similarity-judgment data. In addition, there are multiple approaches to inter-relating the dimension-ratings data and the similarity data. We envision such efforts as involving an extremely long-range project. In the present article, our more limited goal is simply to initiate such an investigation and achieve some first-order characterizations of the underlying structure of the similarity judgments and their relation to the direct dimension-ratings data. In one approach, we conduct classic multidimensional scaling (MDS) analyses of the similarity data, while using the dimension-ratings data to help interpret the derived dimensions of the MDS solutions. In a second approach we investigate the extent to which the dimension-ratings data themselves can be used more directly to predict the observed similarity judgments. For simplicity in these initial analyses, we focus on the averaged data, and leave the characterization of patterns of individual differences in subjects’ similarity judgments as a crucial target for future research. Although there is some danger that analysis of averaged similarity-judgment data can distort patterns observed at the individual-subject level (e.g., Ashby, Maddox, & Lee, 1994; Lee, & Pope, 2003), we will see that the present analyses nevertheless yield results that are highly interpretable.

Non-metric multidimensional scaling

In our first analysis, we applied a standard non-metric-scaling model to the averaged similarity-judgment data (Kruskal, 1964; Shepard, 1962). Although the ideas behind non-metric MDS are well known in the psychological-science community, we provide a brief review here to establish continuity with the subsequent analyses reported in this section. In brief, in the analysis, each stimulus is represented as a point in an M-dimensional space. For simplicity, we assume a Euclidean distance metric for computing distances between the points. Thus, the psychological distance between stimuli i and j is given by

$$ {d}_{ij} = \sqrt{{\displaystyle {\sum}_m{\left({x}_{im}-{x}_{jm}\right)}^2}} $$

(2)

where x _im is the psychological value of stimulus i on dimension m. The MDS program searches for the locations of the points in the space (i.e., the values of the coordinate parameters x _im ) that come as close as possible to achieving a monotonic relation between the derived distances computed from Equation 2 and the judged similarities between the objects. Thus, objects judged as highly similar tend to be located close together in the space, and objects judged as dissimilar tend to be located far away. The departure from a perfect monotonic relation (i.e., the measure of lack of fit) is known as stress (Kruskal & Wish, 1978). As one increases the number of dimensions, one can reduce the stress (i.e., achieve a more nearly monotonic relation between the distances and the similarities), but at the expense of requiring a greater number of free coordinate parameters x _im to achieve this fit.

We used the MDSCALE function from MATLAB to conduct the non-metric scaling analyses. We varied the number of dimensions in the analysis from 1 through 12. Figure 4 shows a plot of stress against the number of dimensions assumed in the analysis. As can be seen, there are large decreases in stress (i.e., improvements in fit) with increases in dimensionality from 1 through about 5, and more gradual decreases in stress thereafter. However, there is no very sharp “elbow” in the plot that points strongly to a particular choice of dimensionality as the most appropriate one. Based on criteria suggested by Kruskal (1964, p. 3), a “good” fit (stress = .05) is achieved in the present case at around 8 dimensions. Although this number of dimensions is large relative to the number of scaled stimuli, we will see shortly that the derived dimensions are in general highly interpretable.

Fig. 4

Plot of stress against number of dimensions for the non-metric multidimensional scaling analyses of the Rocks-30 Similarity-Judgment data

Maximum-likelihood multidimensional scaling

In another approach to investigating the appropriate dimensionality of the rock-similarity space, we conducted a set of analyses that introduced stronger assumptions than used for the non-metric analyses. The idea in these analyses was to use likelihood-based measures of quantitative fit as an approach to assessing the MDS solutions. First, rather than assuming only a monotonic relation between the similarity judgments and the MDS distances, the predicted similarities (ŝ _ij ) were presumed to be a decreasing linear function of the distances (d _ij ):

$$ {\widehat{s}}_{ij}= u- v\cdot {d}_{ij} $$

(3)

Second, following earlier proposals (e.g., Lee, 2001; Tenenbaum, 1996), we assumed that the observed similarity judgments for each pair of stimuli were Gaussian distributed around the predicted value and that these distributions had common variance σ². Given this assumption, then finding the coordinate parameters that maximize the likelihood of the observed similarity-judgment data is equivalent to finding the coordinate parameters that minimize the sum of squared deviations (SSD) between the predicted (ŝ _ij ) and observed (s _ij ) similarity judgments:

$$ S S D = {\displaystyle {\sum}_{i< j}\;{\left({\hat{s}}_{i j}-{s}_{i j}\right)}^2} $$

(4)

Following an early proposal by Lee (2001), we evaluated the fit of MDS models of different dimensionality by using the BIC statistic, which includes a term that penalizes a model as its number of free parameters increases.⁸ As developed by Lee (2001), given the current assumptions, the BIC fit is given by:

$$ B I C= S S D/{\sigma}^2+ P \log (N) $$

(5)

where SSD is given by Equation 4; σ ² is an estimate of the common population variance of the Gaussian-distributed similarity judgments associated with the individual cells; P is the number of free parameters used by the MDS model; and N is the number of observations in the similarity-judgment matrix (N=435 in the present case involving the 30 rock stimuli). In general, with n stimuli embedded in an M-dimensional scaling solution, there are n∙M coordinate parameters that are estimated; however, because pairwise distances between the points are invariant with rigid translations of the space along the coordinate axes, without loss of generality the coordinates of some particular stimulus can all be set to zero, so there are (n-1)∙M free coordinate parameters. In addition, one needs to estimate the parameters (u and v) of the linear function (Equation 3) for transforming distances to similarities. According to this approach, the appropriate dimensionality for the MDS solution is the one that minimizes the BIC statistic: As the number of dimensions (M) increases, the SSD term will grow smaller; however, the penalty term of the BIC statistic grows larger because the number of free parameters P increases.

To implement this model-selection strategy, one needs to specify the variance estimate σ² in the Equation-5 formula. Because in the present application we are interested in evaluating how well the models are predicting the mean similarity judgments in each cell (and because the variability associated with these entries is presumed to be constant across all cells of the matrix), the variance estimate σ² is simply the squared standard-error-of- the-mean, pooled across all cells of the matrix. Recall that a large number of subjects contributed to the estimate of the mean similarity judgment in each individual cell. Thus, there is presumably a great deal of precision in the averaged data. Thus, it is not surprising that the pooled σ² estimate is very small in magnitude: σ²= 0.0557. An implication is that even small improvements in SSD will cause big reductions in the BIC value, so in the present case this model-selection technique will tend to favor high-dimensional MDS models.

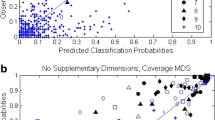
Using the best-fitting non-metric scaling solutions yielded by the MDSCALE program as starting configurations, we conducted computer searches for the values of the coordinate parameters that minimized the BIC statistic described above. We conducted these parameter searches for M=2, 3, 4, 6 and 8 dimensions. The results are reported in Table 4. In addition to reporting the BIC, the table also lists the number of free parameters used by each model, as well as the SSD value and the percentage of variance in the observed similarity judgments accounted for by each model. As can be seen, each increase in dimensionality leads to a better fit of the MDS model according to the BIC statistic. A scatterplot of the observed similarity judgments against the predicted judgments from the eight-dimensional model is provided in the top panel of Fig. 5. The model yields an excellent fit to the observed similarity data, accounting for 96.6% of the variance.

Table 4 Fits of the models to the Rocks-30 Similarity-Judgment data

Fig. 5

Scatterplot of observed against predicted similarity judgments from the Rocks-30 Similarity-Judgment Study. Top panel: Eight-dimensional multidimensional scaling model, bottom panel = ratings-based continuous-distance model. Open circles = subtype pairs from the same high-level category (igneous, metamorphic, sedimentary); crosses = subtype pairs from different high-level categories. Pooled across all pairs, the standard deviation of the pairwise judgments was 1.9891 and the standard error was 0.2361

Figure 5 brings out an interesting aspect of the structure of the similarity-judgment data for the rock categories. In the figure, the open circles represent the mean similarity judgments between pairs of subtypes that belong to the same high-level category (i.e., igneous, metamorphic, or sedimentary); whereas the crosses represent the mean similarity judgments between pairs of subtypes that belong to different high-level categories. It is apparent from inspection that there are numerous cases in which subtypes from different high-level categories are judged as extremely similar to one another, and in which subtypes from the same high-level category are judged as extremely dissimilar to another. This finding provides an initial suggestion that, with respect to perceptual similarities at the high-level, the rock category structures may be highly dispersed (see also Nosofsky et al., 2016). We consider that issue further in our General discussion.

Interpretation of derived dimensions

The next key question is whether the derived MDS configuration yields results that are psychologically and/or scientifically meaningful. For example, do the dimensions of the derived MDS configuration have natural interpretations that correspond to important characteristics of the rock stimuli? Recall that the MDS modeling analyses assumed a Euclidean metric for computing distances between the points in the space. Unfortunately, the Euclidean metric is rotation-invariant: any rigid rotation of the scaling solution will yield the same distances between the points in the space. Thus, the orientation of the scaling solution is arbitrary, so additional analysis is needed to address the question of the interpretability of the derived dimensions.

To address the interpretability question, we conducted Procrustes analyses (e.g., Gower & Dijksterhuis, 2004) in which we rotated, translated, and scaled the derived MDS solution in an attempt to bring it into correspondence with a subset of the dimension ratings obtained in the direct dimension-ratings experiment.⁹ Specifically, based on preliminary inspection of a set of two-dimensional projections of the eight-dimensional MDS solution, we hypothesized that the six dimensions listed in Table 5 were present in its structure. (Based on our visual inspection, we did not have hypotheses regarding the remaining two dimensions.) Let r _im denote the mean rated value of stimulus i on dimension m from the dimension-ratings experiment; and let x _im denote the coordinate value of stimulus i on dimension m following rotation, translation, and scaling of the MDS solution. The “target” MDS solution (produced by rotation, translation and scaling) was defined to be the one that minimized the sum of squared deviations (SSD) between the x _im values and the corresponding r _im values across all 30 stimuli and the six hypothesized dimensions listed in Table 5:

Table 5 Correlations between dimensions 1–6 of the rotated eight-dimensional MDS solution and a set of six hypothesized dimensions from the direct dimension-ratings experiment

$$ S S{D}_{coord}=\kern0.37em {\displaystyle {\sum}_i{\displaystyle {\sum}_m{\left({x}_{i m}-{r}_{i m}\right)}^2.}} $$

(6)

The last step for producing the final rotated MDS solution was then to remove the dimension-scaling operation from the target MDS solution defined above. By doing so, one retains the magnitude of all pairwise distances between points from the originally derived un-rotated MDS solution. The coordinate parameters from this final rotated eight-dimensional solution are reported in the “Multidimensional Scaling Analyses” folder of the article’s website.

In Fig. 6 we provide a plot of this final rotated eight-dimensional MDS solution, with each panel showing the locations of each of the 30 stimuli along each of two dimensions.¹⁰ It is clear from inspection that the first six dimensions are easily interpreted. Dimension 1 corresponds to darkness/lightness of color, with dark rocks located to the left of the space and light rocks located to the right. Dimension 2 corresponds to average grain size: rocks with a very coarse, fragmented grain are located at the top of the space; rocks with a fine or medium grain in the middle; and rocks with little or no visible grain at the bottom. Dimension 3 corresponds to smoothness/roughness of texture, with rough rocks located toward the right and smooth rocks located toward the left. Dimension 4 corresponds to shininess, with shiny rocks located at the top and dull rocks at the bottom. Dimension 5 can be interpreted in terms of the extent to which a rock has an organized versus disorganized texture: Rocks toward the right of the space tend to be composed of organized bands or layers or to have very homogenous grains, whereas rocks toward the left tend to be composed of fragments that seem glued together in haphazard fashion. Finally, Dimension 6 corresponds to chromaticity: Rocks toward the top of the space are chromatic, whereas rocks toward the bottom are mostly neutral white, gray or black. We withhold interpretation of the “left-over” dimensions 7 and 8 at this juncture, although we note that rocks to the upper-right of the space tend to be in the green family, and rocks to the lower left in the red or pink family. This contrast will become more evident in our subsequent analyses of the data from the rocks-360 similarity-judgment study.

Fig. 6

Plot of the rotated eight-dimensional scaling solution that provided a maximum-likelihood fit to the Rocks-30 Similarity Judgment data. Note: axis scales sometimes differ in order to allow better visualization of the rock pictures

To corroborate the interpretations provided above, in Table 5 (left column) we list the correlations between: (i) the coordinate parameters of the 30 rocks on each of the first six rotated dimensions; and (ii) the mean ratings of the 30 rocks on these dimensions from the direct-ratings experiment. The correlations range from .748 to .965 and in all cases are highly significant (p < .001). We should emphasize that it is possible to achieve even higher correlations between the direct dimension ratings and coordinate parameters in the space if a separate rotation of the MDS solution is conducted for each individual dimension. The correlations listed in Table 5 are those that are obtained when the MDS solution is rotated so as to bring it into simultaneous correspondence with all six hypothesized dimensions (as formalized by the SSD measure in Equation 6).

In sum, the present MDS model yields excellent fits to the similarity-judgment data; and the underlying dimensions of the solution have natural interpretations. Thus, it may serve as an excellent starting point for a “feature-space” representation of the rock stimuli that can be used in combination with models of category learning in future work.

A continuous-distance model based on the direct dimension-ratings data

Another question that arises is the extent to which the direct dimension ratings themselves can be used to predict the similarity-judgment data; furthermore, how would such predictions compare to those achieved from the MDS models? As a first step to addressing this question, we formulated a simple “continuous-distance” model based on the dimension ratings. The distance between rocks i and j was given by

$$ {d}_{ij} = {\displaystyle \sum_m}{w}_m\left|{r}_{im}-{r}_{jm}\right|+{C}_{ij} $$

(7)

where r _im is the mean rating of rock i on dimension m, and C _ij is the distance between the rocks on the integral color dimensions of brightness, hue, and saturation (derived from the color-matching condition). The values w _m in Equation 7 are free parameters reflecting the weight given to each rated dimension in computing psychological distance. The color component C _ij in Equation 7 is computed as

$$ {C}_{ij} = \sqrt{w_B{\left|{y}_{iB}-{y}_{jB}\right|}^2+{w}_s{\left|{y}_{iS}-{y}_{jS}\right|}^2+{w}_H\left({\left|{y}_{iH1}-{y}_{jH1}\right|}^2+{\left|{y}_{iH2}-{y}_{jH2}\right|}^2\right)} $$

(8)

where y _iB denotes the value of rock i on the brightness dimension; y _iS the value of rock i on saturation; and y _iH1 and y _iH2 the values of rock i on the circular dimension of hue. The values w _B , w _S and w _H are free parameters reflecting the weight given to brightness, saturation, and hue respectively.¹¹ Finally, the predicted similarity between rocks i and j is given by

$$ {\hat{s}}_{ij}= u- v\cdot {d_{ij}}^{\beta}. $$

(9)

Here, we have allowed for a nonlinear relation between the predicted similarity judgments and the distances d _ij (modeled in terms of the power-exponent β). Our reasoning is that the scale properties of the direct rating judgments are unknown, so it seemed sensible to introduce this first-order form of adjustment to the model.

This ratings-based continuous-distance (RBCD) model makes use of far fewer free parameters than do the MDS models. Whereas in the MDS models, free coordinate parameters x _im were estimated for all the rocks on all M dimensions, in the present model the coordinates of the rocks are held fixed at the values obtained in the independently conducted direct dimension-ratings experiment. Instead, the free parameters consist of only 18 dimension weights (i.e, the w _m values in Equations 7 and 8) and the parameters u, v and β in the similarity function (Equation 9). Furthermore, as noted previously in this article, a number of the rated dimensions are strongly correlated. Thus, it is undoubtedly the case that we could achieve more efficient predictions by defining certain composite dimensions formed from combinations of the individual rated dimensions. For simplicity in these initial analyses, however, we estimate an individual weight parameter for each individual rated dimension.¹²

We fitted the RBCD model to the similarity-judgment data by conducting a computer search for the values of its free parameters that minimized the BIC statistic (Equation 5). The resulting fit is reported along with the MDS models in Table 4. A scatterplot of the observed against predicted similarity judgments is displayed in the bottom panel of Fig. 5. Inspection of the scatterplot suggests that the model provides a good first-order account of the data, but it falls far short of the precise fit yielded by the eight-dimensional MDS model. This assessment is confirmed by a comparison of the BIC fits (Table 4), with the RBCD model yielding a far worse BIC than the eight-dimensional MDS model. On the other hand, it is interesting to note that the RBCD model yields nearly the same SSD and percent-variance-accounted-for as does the two-dimensional MDS model, despite the fact that the two-dimensional MDS model uses nearly three times as many free parameters as does the RBCD model. This result suggests that the direct dimension-ratings data have a good deal of potential utility for future applications.

We discuss possible reasons why the fit of the RBCD model falls far short of the high-dimensional MDS models in our General Discussion, and outline strategies for future extended versions of the model. First, however, we consider the results from the rocks-360 similarity-judgment study.

Analysis of data from the rocks-360 similarity-judgment study

In our view, the question of whether meaningful structure can be extracted from the analysis of the data from rocks-360 similarity-judgment study is an extremely intriguing one. As discussed earlier, because of the huge number of cells in the 360x360 similarity-judgment matrix, the sample size associated with individual cells is extremely small: On average, the mean similarity judgment in each cell is based on only 1.10 entries, with missing data occurring for many of the cells. Thus, at the level of individual cells, the data will be extremely noisy. On the other hand, there is a great deal of redundancy in the matrix: each row i of the matrix provides information concerning the similarity of rock-token i to all other 359 tokens (with the exception of those cells that have missing data). Thus, given the mutual constraints on pairwise similarity between items imposed by the matrix, a structured representation might still emerge from MDS analyses of the data. Because our goal involves the development of a feature-space representation for the complete set of 360 tokens in the rocks library, such a result would have great utility.

We conducted analyses analogous to those we described in the previous section for the rocks-30 similarity-judgment study. Not surprisingly, given the noisy individual-cell data, the non-metric MDS analyses yielded stress values that were, at best, only fair, even for high-dimensional solutions. Therefore, in this section, we move directly to a report of the results from the maximum-likelihood-based MDS analyses.

Maximum-likelihood MDS

Because each of the 253 subjects provided 465 similarity judgments, there was a total of 117,645 individual to-be-predicted data points. We used the same system of MDS equations as in the rocks-30 study (where we predicted mean similarity judgments) for predicting the present individual-trial similarity-judgment data. We conducted computer searches for the maximum-likelihood MDS coordinate parameters for dimensionalities 2, 4, 6, and 8. Note that whereas the MDS models for the rocks-30 data required estimation of 30∙M coordinate parameters (where M is the number of dimensions), fitting the rocks-360 data required estimation of 360∙M coordinate parameters. In addition, to compute the BIC associated with each model, we again require an estimate of the value of σ in Equation 5. Whereas for the rocks-30 data, σ corresponded to the standard-error of the mean in each cell, in the rocks-360 analysis σ corresponds to a variability estimate associated with individual-trial data points. A reasonable approach to setting the value of σ is to use the pooled standard deviation (not standard error) from the rocks-30 data as our estimate for σ in the rocks-360 study.¹³

Because the data are extremely noisy at the level of individual trials, we supplemented our assessment of the models by considering the extent to which they could capture the structure in the collapsed-subtype similarity-judgment matrix as well. As discussed earlier in this article, in this collapsed matrix, we computed the average similarity of all tokens that are members of subtype i to all tokens that are members of subtype j. Recall as well that the entries in the collapsed matrix include the averaged within-subtype similarity judgments among tokens, i.e., the entries along the main diagonal of the collapsed 30 x 30 matrix.

The fits of the MDS models to the rocks-360 data are reported in Table 6. Not surprisingly, the models account for a relatively small percentage of variance in the individual-trials data. Nevertheless, the higher-dimensional models account for an extremely large percentage of variance in the data of the collapsed subtype matrix. A scatterplot of observed-against-predicted collapsed similarity judgments for the eight-dimensional model is provided in the top panel of Fig. 7.

Table 6 Fits of the models to the Rocks-360 Similarty-Judgment data

Fig. 7

Scatterplot of observed against predicted similarity judgments for the collapsed subtype matrix from the Rocks-360 Similarity-Judgment Study. Top panel: eight-dimensional multidimensional scaling model, bottom panel = ratings-based continuous-distance model. Solid circles = within-subtype pairs; open circles = between-subtype pairs from the same high-level category (igneous, metamorphic, sedimentary); crosses = between-subtype pairs from different high-level categories. Pooled across all pairs, the standard deviation of the pairwise judgments in the collapsed matrix was 2.1544

With regard to the collapsed-matrix scatterplot, we have again represented different types of pairs with different symbols. The open circles denote subtype pairs from within the same high-level category (igneous, metamorphic, sedimentary), and the crosses represent pairs from different high-level categories. As was the case for the rocks-30 similarity-judgment data, there are numerous cases in which judged similarity between subtypes that belong to different high-level categories is very high, and numerous cases in which similarity between subtypes that belong to the same high-level category is very low. Whereas for the rocks-30 study that result pertained only to specific representative tokens of each subtype, here the result is far more general: it pertains to the average similarity between large numbers of tokens of each of the subtypes. The Fig. 7 scatterplot also indicates the average within-subtype judged similarities (the solid circles). It is interesting to note that the subtypes vary considerably in their degree of within-class similarity. For example, some subtypes, such as anthracite, were composed of a set of tokens that subjects judged to be highly homogeneous (mean similarity = 7.35); whereas others, such as rhyolite, were composed of tokens that were highly dispersed (mean similarity = 4.37). Indeed, there are many cases in which the mean similarity between tokens of different subtypes greatly exceeds the mean similarity of tokens within the same subtype. For example, the mean of the similarity ratings between the tokens of anthracite and obsidian was 6.47, far greater than the “self-similarity” of rhyolite (and a number of other rock subtypes). This variability in both between-subtype and within-subtype similarity is well captured by the high-dimensional MDS models.

According to the BIC assessment in Table 6, for the rocks-360 data, the six-dimensional MDS model is actually favored compared to the eight-dimensional model. The intuition is that because there is a lack of precision associated with the individual-trials data, adding free coordinate parameters beyond six dimensions is not justified relative to the improvement in absolute fit that is achieved. Despite this recommendation provided by the BIC analysis, we will nevertheless report below the results from the eight-dimensional solution. As will be seen, the reason is that clear interpretations are available from the eight-dimensional solution and these interpretations seem too compelling to be ignored.

Interpretation of derived dimensions

We used the same approach to searching for structure in the MDS solution as we used for the rocks-30 study. The only difference is that the analysis now involved establishing correspondences between the coordinate parameters and dimension ratings associated with all 360 rock tokens, rather than just the 30 representative tokens from the rocks-30 study.

Following rotation of the space to achieve the correspondences, the resulting MDS plots are pictured in Figs. 8, 9, 10 and 11. (The tabled coordinates as well as interactive versions of the MDS plots are provided in the article’s website.) It is clear from inspection that the first six dimensions again have natural interpretations in terms of: (i) lightness of color, (ii) average grain size, (iii) smoothness/roughness, (iv) shininess, (v) organization, and (vi) chromaticity. As listed in the third column of Table 5, there are again high correlations between the coordinate-parameter values on these dimensions and the direct dimension ratings (p < .001 in all cases).

Fig. 8

Plot of the rotated eight-dimensional scaling solution that provided a maximum-likelihood fit to the Rocks-360 Similarity Judgment data. Dimensions 1 versus 2. Note: axis scales sometimes differ in order to allow better visualization of the rock pictures

Fig. 9

Plot of the rotated eight-dimensional scaling solution that provided a maximum-likelihood fit to the Rocks-360 Similarity Judgment data. Dimensions 3 versus 4. Note: axis scales sometimes differ in order to allow better visualization of the rock pictures

Fig. 10

Plot of the rotated eight-dimensional scaling solution that provided a maximum-likelihood fit to the Rocks-360 Similarity Judgment data. Dimensions 5 versus 6. Note: axis scales sometimes differ in order to allow better visualization of the rock pictures

Fig. 11

Plot of the rotated eight-dimensional scaling solution that provided a maximum-likelihood fit to the Rocks-360 Similarity Judgment data. Dimensions 7 versus 8. Note: axis scales sometimes differ in order to allow better visualization of the rock pictures

Although the rated dimension corresponding to Dimension 6 was chromaticity, it appears that an even stronger interpretation is that the dimension corresponds to “coolness” versus “warmness” of color. That is, not only are the chromatic colors located toward the top of the space, but there is also a clear division between the warm colors (red, orange, and yellow) and the cool colors (green and blue). Possibly, some composite of chromaticity and coolness/warmness provides the best overall description. In future work, we plan to collect direct ratings of coolness and warmness to substantiate this interpretation.

Inspection of the “left-over” dimensions 7 and 8 (see Fig. 11) suggests additional structure that is present in the MDS solution. For Dimension 8, we see a separation between colors in the green family and colors in the pink and red family, with neutral colors occupying the middle ground. This pattern motivated us to plot Dimension 6 against Dimension 8, with the result shown in Fig. 12. The combination of these dimensions is strongly reminiscent of the classic color circle: starting from the upper-left of the space and proceeding clockwise, one moves through red, orange, yellow, green, blue, purple, pink, and back to red again. In this depiction, the neutral achromatic colors are bunched to the lower left, closer to the cool colors than to the warm ones.

Fig. 12

Plot of the rotated eight-dimensional scaling solution that provided a maximum-likelihood fit to the Rocks-360 Similarity Judgment data. Dimensions 8 versus 6. This combination of dimensions is shown to reveal the role of the “color circle” in influencing the subjects’ similarity judgments

Finally, inspection of Dimension 7 (see Fig. 11) suggests that shape-related aspects of the rocks may also have influenced the subjects’ similarity judgments: Rocks toward the left of the space are often flat and two-dimensional, whereas rocks toward the right are spherical or cube-like. However, this shape-related variation does not appear to be as systematic as the forms of variation that underlie the other dimensions.

Ratings-based continuous-distance (RBCD) model

We fitted the RBCD model to the rocks-360 similarity-judgment data in the same manner as already described for the rocks-30 data. An important point to note about the application of the model is that despite the large increase in the number of stimuli (n=360 rather than n=30), the RBCD model uses the same number of free parameters as before: 18 dimension-weight parameters and the three parameters that define the similarity-transform function (Equations 7–9). By comparison, as described in the previous section, application of the MDS models required an enormous increase in the number of free parameters compared to the rocks-30 study.

The fit of the RBCD model is reported along with the MDS models in Table 6, and a scatterplot of observed-against-predicted similarity judgments for the collapsed matrix is provided in the bottom panel of Fig. 7. It is interesting to note that, even without the penalty for number of free parameters, the absolute SSD fit of the RBCD model with 21 free parameters is better than that of the two-dimensional MDS model with 720 free parameters. Still, the BIC statistic picks out the six-dimensional MDS model as providing a substantially better account of the data than the RBCD model. This pattern is similar to what we observed from the modeling of the rocks-30 similarity-judgment data. It suggests that although the direct dimension ratings have a great deal of utility, there may be some limitations associated with directly applying them to derive a feature-space representation for the rock stimuli. We consider this issue in more detail in our General discussion.

General discussion

Summary

In this article we have taken first steps toward the building of a feature-space representation for a complex and ubiquitous natural category domain, namely the world of rocks. The stimuli are a set of 360 images representing 12 tokens each of 30 common subtypes of igneous, metamorphic, and sedimentary rocks. The data are direct dimension ratings for all 360 rocks along a set of 18 hypothesized dimensions, as well as two sets of similarity judgments among pairs of the rocks. (Some information pertaining to mechanical and chemical properties of the rocks is also provided.) The stimuli and detailed data sets, as well as results from initial multidimensional scaling analyses, are available on the website https://osf.io/w64fv/. We believe these data will be useful for a wide variety of research purposes, including: (i) probing the statistical and psychological structure of a complex natural category domain, (ii) testing models of similarity judgment, and (iii) developing a feature-space representation that can be used in combination with formal models of category learning to predict classification performance in this domain.

Future research directions

Extending the list of dimensions. In our view, this report represents a major first step in the data-collection process and associated data analyses for this domain, but we envision that much future work will be aimed at developing still richer characterizations of the rock category structures. For example, although we believe that the dimensions that we selected for the direct-ratings study provide a good first-order sampling of most of the primary dimensions of the rocks, there are other dimensions that likely play a significant role. For example, our analyses of the similarity-judgment data provided hints that certain shape-related dimensions, not included in our direct-dimension ratings, may be important. Likewise, we will need to add certain second-order features of a more subtle nature to the data base. For example, a characteristic feature of many tokens of marble and quartzite is the presence of swirls or veins; granite can be discriminated from diorite due to the presence of quartz crystals; and schist is characterized by visible mineral grains of mica that have distinct plate-like crystal formations. Future direct dimension-ratings studies can be conducted to expand the initial data base that we have collected.

Similarity-judgment models. One of the questions we addressed in our initial analyses was the extent to which the direct dimension ratings themselves could be used to predict the various forms of similarity-judgment data. Similar questions have been addressed in other domains in previous research. For example, De Deyne, Verheyen, Ameel, et al. (2008) reported the results of a feature-generation task for the exemplars of 15 semantic categories. A variety of other measures, such as similarity judgments among exemplars, were also collected. Zeigenfuse and Lee (2010) subsequently used an additive clustering model formulated within a hierarchical Bayesian framework to interrelate the feature-generation data and a subset of the similarity-ratings data. Their primary goal was to characterize the importance of the individual features for explaining the similarities among the exemplars. (This goal of characterizing feature importance will be a major target in future investigations of the present domain as well.) The researchers did not conduct investigations, however, of how well the additive-clustering model (combined with the pre-generated features) compared to alternative models in accounting for the similarity data.

In the present research, we made explicit comparisons between the performance of the ratings-based continuous-distance (RBCD) model and MDS models of similarity judgment. For the data set involving the 360 rock tokens (with 117,645 data points), the RBCD model – with only 21 free parameters – yielded fits that were even better than those of a two-dimensional MDS model – with 720 free parameters. This type of result highlights the potential utility of the dimensions-ratings data for generating predictions of performance in independent tasks involving these stimuli. Nevertheless, the direct dimensions-rating model fell substantially short of higher-dimensional MDS models in fitting the data (although the number of free parameters used by the latter models was two orders of magnitude greater than the number used by the RBCD model).

On the one hand, we believe that the approach based on collecting direct dimension ratings can have enormous utility for future investigations in this domain. For example, suppose that one wished to expand the set of rock instances in future experiments involving memory or categorization of these stimuli. And suppose that theoretical analyses of the data from such experiments required a feature-space representation for these additional stimuli. Assuming n additional stimuli, and M rated dimensions, then something roughly on the order of n∙M additional ratings would be involved. By comparison, in the absence of heuristic shortcuts, a conventional similarity-scaling approach for locating the new stimuli in the feature space would require something on the order of n∙(360+n) new judgments: namely, an assessment of the similarity of each of the n new stimuli to one another and to the original 360 stimuli in the set. Thus, the data-collection process involving the direct dimension ratings would be orders of magnitude more efficient than a conventional similarity-scaling approach.

In addition, as we argued in our Introduction, certain forms of information may simply be left out of MDS representations derived from the scaling of similarity-judgment data, yet be critical for the purpose of categorization. For the present domain, a potential case in point involves the MDS dimension of “organization.” In this example, highly organized rocks composed of stripes, physical layers, or homogeneous grains were located at one pole of the space, whereas rocks composed of unorganized fragments were located at the opposite pole. However, whether a rock is composed of stripes versus physical layers versus homogeneous grains is crucial for purposes of classifying the rock into categories, and it is unclear that this more subtle form of information was captured by the MDS representation. Thus, having direct ratings for these more subtle distinctions may have great utility.

Nevertheless, despite the potential utility of the direct dimension-ratings data, the bottom line is that our formal ratings-based continuous-distance (RBCD) model fared worse than did the MDS models in predicting the similarity-judgment data for the rocks. In our view, the underlying basis for these limitations needs to be resolved in future work: The limitations of the RBCD model in accounting for the similarity judgments might also arise in other tasks such as category learning. We should note that in this initial investigation, we used the BIC statistic for making comparisons of fit in these cases involving models that mismatched in their numbers of free parameters. Future work should consider other approaches to comparing the various similarity-judgment models, including methods based on cross-validation or generalization testing (e.g., Steyvers & Busey, 2000; Verheyen, Ameel, & Storms, 2007), or posterior predictive fit from Bayesian parameter integration (e.g., Lee, 2008).

There is a wide variety of possible explanations for the apparent limitations of the direct dimension-ratings approach to predicting the similarity-judgment data (compared to the high-dimension MDS models). First, as noted above, there may be other dimensions that contributed to subjects’ similarity judgments that were not included in our initial set of ratings. With their very large numbers of free parameters, the MDS models can incorporate such influences by “shuffling” the coordinate parameters of the objects, such that the derived dimensions reflect composites of influences. For example, the dimension that corresponds most closely to “average grain size” might also reflect influences of the presence of swirls and veins, quartz crystals, and so forth. Second, our formal modeling assumed a linear relation between the psychological scale values for the stimuli and the dimension ratings; however, the true relation may be highly nonlinear in form, and the precise form may differ from one dimension to another. Third, our similarity-judgment modeling was aimed either at averaged data (rocks-30) or at aggregated individual-subject data (rocks-360). Conceivably, different patterns of model-comparison results might arise if models that are sensitive to individual differences are tested (e.g., Carroll & Wish, 1974; Lee & Pope, 2003; Okada & Lee, 2016). Fourth, all models considered in the present article were spatial models that relied on measures of continuous distance. As an alternative, additive clustering and tree models might be applied (Corter, 1998; Sattath & Tversky, 1977; Shepard & Arabie, 1979), which are based on matching and mismatching of discrete features. In the present complex stimulus domain, we believe that hybrid models that combine spatial and discrete-feature components might prove to be particularly valuable (e.g., Lee & Navarro, 2002; Nosofsky & Zaki, 2003; Verguts, Ameel, & Storms, 2004). For example, it seems likely that matches between two rocks on a relatively rare feature, such as the presence of holes, would lead to boosts in the judged similarity between the two objects. Such boosts are not easily captured by models that rely solely on the construct of continuous distance.

Rather than placing the MDS and RBCD models in competition, perhaps the best approach to deriving an optimal feature representation for the rocks would be one that combines elements of the direct-dimension ratings and similarity-scaling methods. For example, models based on the derived feature representation might be required to simultaneously fit the dimension-ratings and the similarity-judgment data. This approach would involve specifying error models for both the similarity-judgment data and the dimension-ratings data and searching for the feature space that maximized the joint likelihood of both data sets. The dimension-ratings data would thereby provide constraints on the MDS solutions derived for the rock stimuli. Such constraints might reduce any tendency for the high-parameter MDS solutions to “fit the noise” in the similarity data, thereby yielding a more stable and robust feature-space representation. An alternative approach might involve directly supplementing the MDS solutions with appended information provided from the direct dimension ratings. In this approach, the MDS solution would provide the bedrock feature space, but it would be supplemented by ratings along additional dimensions that were not recovered from the modeling of the similarity judgment data. This hybrid feature-space representation would then be used for predicting performance in independent tasks of interest.

Making use of the rocks feature-space representation. Once we have settled upon a detailed and reliable feature-space representation, a wide variety of new questions can be pursued. To begin, there is the question of the overall statistical structure of the rock-category space. In the cognitive-psychology of category learning, researchers have hypothesized about the structure of natural categories, and these hypotheses have motivated influential theories of the nature of category representation and decision making. For example, in their classic paper, Rosch and Mervis (1975) suggested that natural categories are held together via a “family-resemblance” principle, in which members of the same category share bundles of characteristic features that are not shared by members of contrasting categories. This principle produces structures in which there tends to be high within-category similarity and low between-category similarity. The family-resemblance ideas were influential in promoting previously proposed “prototype” models of categorization, in which people are presumed to represent categories in terms of summary statistics such as the central-tendency of the category (e.g., Posner & Keele, 1968; Reed, 1972; Smith & Minda, 1998). Other researchers have suggested related ideas such as that the statistical structure of natural categories may be well modeled in terms of multivariate normal distributions (e.g., Ashby & Gott, 1988; Fried & Holyoak, 1984). Such ideas helped motivate the influential “decision bound” models of categorization, in which observers classify objects in accord with parametric likelihood functions, including linear and quadratic discriminant functions (Ashby & Gott, 1988).

These hypotheses involving the structure of natural categories are well grounded from theoretical and rational perspectives; however, to our knowledge, researchers have not previously conducted rigorous and detailed empirical investigations of the actual statistical structure of complex, real-world categories to test these motivating hypotheses. Nosofsky et al. (2016) recently provided some preliminary evidence bearing on these issues. In particular, they presented three-dimensional and four-dimensional scaling solutions of the present rocks-30 similarity-judgment data. Those scaling solutions suggested that – when considered at the high level of igneous, metamorphic, and sedimentary rocks – the categories are disorganized and dispersed, and do not seem to be structured in accord with a family-resemblance principle. However, that earlier work was limited in that the researchers made use of only a single representative token per rock-category subtype and considered the structure of only low-dimensional scaling solutions for the rocks. Once an adequate high-dimensional feature space for the present library of 360 rocks is derived, we will have a much stronger data base for investigating these issues. Furthermore, alternative “attention weightings” of the dimensions in the space might conceivably be available that convert the dispersed category structures into ones that obey the family-resemblance principle (e.g., Nosofsky, 1986). If so, one could test whether or not experts in the geologic sciences have learned these dimensional attention weightings. Still another possibility is that a family-resemblance or multivariate-normal model would provide a good account of the rock category structures if considered at the subtype level (e.g., granite, diorite, basalt, etc.) rather than at the high level of igneous versus metamorphic versus sedimentary.

Once an adequate feature-space representation is derived, we can also move towards our primary goal of using that representation in combination with formal models of category learning to generate predictions of classification performance in this complex domain. Although formal models of perceptual classification have been thoroughly compared and contrasted in simple perceptual domains involving artificial category structures (for a review, see Pothos & Wills, 2011), there is much less work in applying the models to problems of perceptual categorization in the real world. The present research provides the initial steps needed for this form of translation.

Prospects for generality

Finally, although our example target domain in this research was the world of rocks, it seems reasonable that the general method can be used for generating feature-space representations for a wide variety of naturalistic stimuli, including plants, flowers, birds, fungi, and so forth. Consider, for example, the categories of types of leaves. There are roughly 50 different oak species in eastern North America alone and it can be extremely challenging to identify different types of oak leaves (Stein, Binion, & Acciavatti, 2003). In the same manner that geologists have delineated major characteristics of rocks, so have botanists delineated major characteristics of leaf morphology (as well as other characteristics of leaves such as color, pubescence, and so forth). For example, as detailed in Stein et al.’s (2003) description of the leaves of different oak species, major attributes of leaf morphology include the overall shape of the leaf; type of edge or margin; the nature of the clefts or lobes; and the arrangement of veins in the leaf. For example, the leaf margin may be smooth, undulating, serrated, and so forth. Thus, in the same manner as we collected direct ratings for our listing of primary dimensions for the categories of rocks, it seems reasonable that direct ratings can be obtained for leaf characteristics. Furthermore, one could also collect similarity judgments among different tokens of the leaf categories, and the direct-dimension ratings and similarity judgments could be used to inform one another, in the same manner as illustrated for the rock stimuli in the present research. Questions could then be pursued concerning the statistical and psychological structure of the leaf categories, and the derived scaling representations could serve as the foundation for application of formal models of memory and categorization. Thus, the approach that we pursued in the present work should be generally applicable to other naturalistic domains. Indeed, our hope is that our approach will ultimately be useful for allowing formal modeling in perceptual category learning to help guide strategies for the teaching of a wide variety of scientific classifications in the classroom and the field.

Appendix

Table 7 Mean ratings for each of the rock subtypes along each of dimensions 1-17

Table 8 Standard deviation of ratings for each of the rock subtypes along each of dimensions 1-17, using tokens as the unit of analysis