1 Introduction

In most economic and financial processes, mathematical modeling leads to nonlinear delayed dynamical systems, and the interplay of delayed and nonlinear effects is important for many reasons. Capturing the price behavior of commodity and forecasting future developments are essential in commodity management and international policy. Given this, fluctuations in commodity price have long been, and will continue to be, one of the dominant topics in mathematical economics due to its universal existence and importance. Based on some mathematical assumptions, various price adjustment models have been developed to analyze the problems in economics, see [1–4] and the references cited therein.

One of the representative models was introduced by Mackey [5, 6], who considered a price adjustment model for a single commodity market with state dependent production and storage delays in the following form:

$$ \frac{P'(t)}{P(t)}=D\bigl(P(t)\bigr)-S\bigl(P_{s}(t)\bigr). $$
(1)

Here \(P(t)\) is the market price of a particular commodity at time t, and D and S refer to demand and supply functions, respectively. It is assumed that the consumers base their buying decisions on current market prices. For most commodities, there is a finite time τ that elapses before a change in production occurs. Assuming that only the market price at time \(t-\tau\) has an effect on the current supply price \(P_{s}(t)\), we get \(P_{s}(t)=P(t-\tau)\) (see [5] for more details). Farahani and Grove [7] considered the following special case:

$$ \frac{P'(t)}{P(t)}=\frac{a}{b+P^{n}(t)}-\frac{cP^{m}(t-\tau)}{d+P^{m}(t-\tau)}, $$
(2)

where \(a, b, c, d, m, \tau>0\), and \(n\geq1\). For system (2), global convergence of the positive equilibrium was investigated in [8, 9], global attractivity of solutions was discussed in [10]. In addition, the existence of almost periodic solutions for an impulsive delay model was established in [11, 12].

However, the dynamic behaviors of system (2) still need further investigation. In this paper, we are trying to improve the understanding of the complex dynamics induced by time delay. Motivated by the conjecture on global bifurcation results in [8], we shall focus on the global continuation of a local Hopf bifurcation. In the following sections, the stability of a unique positive equilibrium and a local Hopf bifurcation analysis for system (2) are presented. After that, the global existence of bifurcating periodic solutions is explored with the assistance of global Hopf bifurcation theory developed by Wu [13], and related applications can be found in [14–17]. Finally, some numerical simulations are performed to illustrate the theoretical results.

2 Local Hopf bifurcation analysis

In light of the monotonicity of demand and supply functions, system (2) has a unique positive equilibrium \(P_{\ast}\) such that \(a/(b+P_{\ast}^{n})=cP_{\ast}^{m}/(d+P_{\ast}^{m})\). Based on Taylor’s formula, the linearized system of (2) at \(P_{\ast}\) is as follows:

$$ \frac{\mathrm{d}P}{\mathrm{d}t}=-\alpha P(t)-\beta P(t-\tau), $$
(3)

where \(\alpha=anP_{\ast}^{n}/(b+P_{\ast}^{n})^{2}>0\) and \(\beta=cdmP_{\ast}^{m}/(d+P_{\ast}^{m})^{2}>0\). When we define that \(P(t)=e^{\lambda t}\) and substitute it into (3), we can get the following first order transcendental characteristic equation:

$$ \lambda+\alpha+\beta e^{-\lambda\tau}=0. $$
(4)

It is evident that the characteristic root is \(\lambda=-(\alpha+\beta )<0\) when \(\tau=0\). On the other hand, equation (4) has infinitely many roots as \(\tau>0\), and these roots vary with τ. According to Corollary 2.4 in [18], the sum of characteristic roots in the open right half-plane can change only if a root appears on or crosses the imaginary axis. In order to establish the number of roots with positive real parts, we assume that \(\lambda=i\omega\) (\(\omega >0\)) is a root of (4). Then

$$i\omega+\alpha+\beta(\cos\omega\tau-i\sin\omega\tau)=0. $$

By separating the real and imaginary parts, we get the following:

$$\left \{ \textstyle\begin{array}{l} \alpha+\beta\cos\omega\tau=0, \\ \omega-\beta\sin\omega\tau=0. \end{array}\displaystyle \right . $$

Adding the squares of both equations together gives the following:

$$\omega^{2}=\beta^{2}-\alpha^{2}. $$

Clearly, equation (4) has a pair of purely imaginary roots \(\pm i \omega_{0}\) when \(\beta>\alpha\) and \(\tau=\tau_{k}\) (\(k=0,1,2,\ldots\)), where

$$\omega_{0}=\sqrt{\beta^{2}-\alpha^{2}}, \qquad \tau_{k}=\frac{1}{\omega_{0}}\biggl\{ \arccos \frac{-\alpha}{\beta}+2k\pi \biggr\} . $$

Then we verify the transversality condition. Let \(\lambda_{k}=\eta_{k}(\tau)+i\omega_{k}(\tau)\) denote a root of (4) near \(\tau=\tau_{k}\) such that \(\eta_{k}(\tau_{k})=0\), \(\omega_{k}(\tau _{k})=\omega_{0}\). Substituting \(\lambda_{k}\) into (4) and differentiating with respect to τ, we get

$$\frac{\mathrm{d}\lambda}{\mathrm{d}\tau}-\beta e^{-\lambda\tau} \biggl( \lambda+\tau\frac{\mathrm{d}\lambda}{\mathrm{d}\tau} \biggr)=0, $$

thus

$$\begin{aligned} \frac{\mathrm{d}\lambda}{\mathrm{d}\tau} \bigg|_{\lambda=i\omega _{0},\tau=\tau_{k}} =& \frac{\beta\lambda e^{-\lambda\tau}}{1-\beta \tau e^{-\lambda\tau}} \bigg|_{\lambda=i\omega_{0},\tau=\tau_{k}} \\ =& \frac{i\beta\omega_{0}(\cos\omega_{0}\tau_{k}-i\sin\omega_{0}\tau _{k})}{1-\beta\tau_{k}\cos\omega_{0}\tau_{k}+i\beta\tau_{k}\sin\omega_{0}\tau_{k}} \\ =& \frac{\omega_{0}^{2}-i\alpha\omega_{0}}{1+\alpha\tau_{k}-i\omega_{0}\tau_{k}}, \end{aligned}$$

and

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau}\operatorname{Re}\bigl(\lambda(\tau_{k})\bigr) =& \frac{\omega _{0}^{2}(1+\alpha\tau_{k})-\omega_{0}^{2}\alpha\tau_{k}}{(1+\alpha\tau_{k})^{2}+(\omega _{0}\tau_{k})^{2}} \\ =&\frac{\omega_{0}^{2}}{(1+\alpha\tau_{k})^{2}+(\omega_{0}\tau_{k})^{2}} \\ >&0. \end{aligned}$$

Due to the above inequality, we can deduce that the number of characteristic roots with positive real parts will increase by two when time delay τ passes the critical values \(\tau_{k}\) each time.

Through the above analysis, we can determine the distribution of roots of (4) as follows.

Lemma 1

For equation (4), the following claims are true:

  1. (i)

    If \(\beta\leq\alpha\), then all roots of (4) have negative real parts for any \(\tau\geq0\).

  2. (ii)

    If \(\beta>\alpha\), then (4) has a pair of imaginary roots \(\pm i\omega_{0}\) when \(\tau=\tau_{k}\) (\(k=0,1,2,\ldots\)).

  3. (iii)

    If \(\beta>\alpha\), then all roots of (4) have negative real parts only when \(\tau\in[0,\tau_{0})\). Equation (4) has \(2(k+1)\) roots with positive real parts when \(\tau\in(\tau_{k},\tau_{k+1}]\).

According to the results regarding the stability of equilibrium in [19], we have the following theorem about the stability of positive equilibrium and the existence of a local Hopf bifurcation.

Theorem 1

For system (2), we have:

  1. (i)

    if \(\beta\leq\alpha\), then the positive equilibrium \(P_{\ast}\) is asymptotically stable;

  2. (ii)

    if \(\beta>\alpha\), then the positive equilibrium \(P_{\ast}\) is stable when \(\tau<\tau_{0}\) and unstable when \(\tau>\tau_{0}\). Moreover, a Hopf bifurcation occurs at the critical value \(\tau_{k}\), and periodic solutions will bifurcate from \(P_{\ast}\).

By using the normal form theory and the center manifold theorem developed by Hassard [20] and the calculation methods in [21], we can determine the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions. Next, we shall briefly give the formulae for determining the bifurcation properties at the first bifurcation value \(\tau_{0}\).

For convenience, we rewrite some notations as follows:

$$D\bigl(P(t)\bigr)=\frac{a}{b+P^{n}(t)},\qquad S\bigl(P(t-\tau)\bigr)= \frac{cP^{m}(t-\tau )}{d+P^{m}(t-\tau)}. $$

Following the algorithms in [14, 20], we can obtain the crucial coefficients which will be used in determining the bifurcation properties:

$$\begin{aligned}& g_{20}=\overline{D}\tau_{0} \bigl[ 2D'(P_{\ast})+P_{\ast}D''(P_{\ast}) +P_{\ast}S''(P_{\ast})e^{-i\omega_{0}\tau_{0}} \bigr], \\& g_{11}=\overline{D}\tau_{0} \bigl[ 2D'(P_{\ast})+P_{\ast}D''(P_{\ast}) +P_{\ast}S''(P_{\ast}) \bigr], \\& g_{20}=\overline{D}\tau_{0} \bigl[ 2D'(P_{\ast})+P_{\ast}D''(P_{\ast}) +P_{\ast}S''(P_{\ast})e^{i\omega_{0}\tau_{0}} \bigr], \\& g_{20}=\overline{D}\tau_{0} \bigl\{ \bigl[4D'(P_{\ast})+2P_{\ast}D''(P_{\ast})\bigr]W_{11}(0) +3D''(P_{\ast}) +P_{\ast}D'''(P_{\ast}) \\& \hphantom{g_{20}={}}{}+\bigl[2D'(P_{\ast})+P_{\ast}D''(P_{\ast})\bigr]W_{20}(0)+ P_{\ast}S''(P_{\ast})e^{i\omega_{0}\tau_{0}}W_{20}(-1) \\& \hphantom{g_{20}={}}{}+2P_{\ast}S''(P_{\ast}) e^{-i\omega_{0}\tau_{0}}W_{11}(-1)+P_{\ast}S'''(P_{\ast}) e^{-i\omega_{0}\tau_{0}} \bigr\} , \end{aligned}$$

where

$$\begin{aligned}& D=\frac{1}{1-\tau_{0}\alpha-i\omega_{0}\tau_{0}}, \\& W_{20}(\theta)=-\frac{g_{20}}{i\omega_{0}\tau_{0}}e^{i\omega_{0}\tau_{0}\theta} -\frac{\overline{g}_{02}}{3i\omega_{0}\tau_{0}} e^{-i\omega_{0}\tau_{0}\theta} +E_{1} e^{2i\omega_{0}\tau_{0}\theta}, \\& W_{11}=\frac{g_{11}}{i\omega_{0}\tau_{0}}e^{i\omega_{0}\tau_{0}\theta} -\frac {\overline{g}_{11}}{i\omega_{0}\tau_{0}}e^{-i\omega_{0}\tau_{0}\theta} +E_{2}, \end{aligned}$$

and

$$\begin{aligned}& E_{1}=\frac{2D'(P_{\ast})+P_{\ast}D''(P_{\ast})+P_{\ast}S''(P_{\ast})e^{-i\omega _{0}\tau_{0}}}{2i\omega_{0}+\alpha+\beta e^{-i\omega_{0}\tau_{0}\theta}}, \\& E_{2}=\frac{2D'(P_{\ast})+P_{\ast}D''(P_{\ast})+P_{\ast}S''(P_{\ast})}{\alpha +\beta}. \end{aligned}$$

Consequently, we can calculate the following quantities:

$$\begin{aligned}& c_{1}(0)=\frac{i}{2\omega_{0}\tau_{0}} \biggl( g_{11}g_{20}-2|g_{11}|^{2}- \frac {|g_{02}|^{2}}{3} \biggr) +\frac{g_{21}}{2} , \\& \mu_{2}=-\frac{\operatorname{Re}(c_{1}(0))}{\operatorname{Re}(\lambda' (\tau_{0}))} , \\& \beta_{2}=2\operatorname{Re}\bigl(c_{1}(0)\bigr) , \\& T_{2}=-\frac{\operatorname{Im}(c_{1}(0))+\mu_{2}\operatorname{Im}(\lambda'(\tau_{0}))}{\omega _{0}\tau_{0}} . \end{aligned}$$

It is well known that \(\mu_{2}\) determines the direction of the Hopf bifurcation: the Hopf bifurcation is supercritical (subcritical) and the bifurcating periodic solutions exist for \(\tau>\tau_{0}\) (\(\tau<\tau _{0}\)) if \(\mu_{2}>0\) (\(\mu_{2}<0\)); \(\beta_{2}\) determines the stability of bifurcating periodic solutions: the bifurcating periodic solutions are orbitally asymptotically stable (unstable) if \(\beta_{2}<0\) (\(\beta_{2}>0\)); \(T_{2}\) determines the period of the bifurcating periodic solutions: the period increases (decreases) if \(T_{2}>0\) (\(T_{2}<0\)).

It is not difficult to find that the derivatives of demand and supply functions at the positive equilibrium \(P_{\ast}\) have significant effects on the properties of a local Hopf bifurcation.

3 Global bifurcation analysis

It is known that periodic solutions through Hopf bifurcation are generally local and only exist in a small neighborhood of the critical value. Hence it is interesting and significant to verify the global existence of bifurcating periodic solutions. In this section, we study the global continuation of periodic solutions bifurcating from the positive equilibrium \(P_{\ast}\) of system (2).

Following the work of [13], we need to show the uniform boundedness of the periodic solutions of (2) and the nonexistence of τ-periodic solutions.

Lemma 2

If \(a>bc\), and m and n are even integers, then all periodic solutions of (2) are uniformly bounded.

Proof

Let \(P(t)\) be a nonconstant periodic solution of (2) and define that

$$A= P(t_{1})=\max\bigl\{ P(t) \bigr\} ,\qquad B=P(t_{2})=\min \bigl\{ P(t)\bigr\} , $$

and

$$\dot{P}(t_{1})=\dot{P}(t_{2})=0, $$

which is equivalent to

$$\left \{ \textstyle\begin{array}{l} \frac{a}{b+A^{n}}=\frac{cP^{m}(t_{1}-\tau)}{d+P^{m}(t_{1}-\tau)}, \\ \frac{a}{b+B^{n}}=\frac{cP^{m}(t_{2}-\tau)}{d+P^{m}(t_{2}-\tau)}. \end{array}\displaystyle \right . $$

From the second equation and the even quality of m and n, we have

$$\frac{a}{b+B^{n}}< c \quad \mbox{and}\quad B^{n}>\frac{a}{c}-b. $$

Thus

$$B>\sqrt[n]{\frac{a}{c}-b}. $$

On the contrary, we have

$$\frac{a}{b+A^{n}}\geq\frac{cB^{m}}{d+B^{m}} \quad \mbox{and}\quad \frac{A^{n}}{a}\leq \frac{d+B^{m}}{cB^{m}}-\frac{b}{a}. $$

Hence

$$A\leq\sqrt[n]{a \biggl( \frac{d+B^{m}}{cB^{m}}-\frac{b}{a} \biggr) }. $$

This completes the proof. □

Lemma 3

If m and n are even, then system (2) has no τ-periodic solution.

Proof

Assume that system (2) has a τ-periodic solution, then the following ordinary differential equation

$$ \frac{\mathrm{d}P}{\mathrm{d}t}=P(t) \biggl( \frac{a}{b+P^{n}(t)}- \frac {cP^{m}(t)}{d+P^{m}(t)} \biggr) $$
(5)

has a nonconstant periodic solution.

Because m and n are even integers, system (5) has three steady states \(P(t)=0\), \(P(t)=P_{\ast}\) and \(P(t)=-P_{\ast}\). In system (5), \(\dot{P}(t)<0\) holds when \(P(t)>P_{\ast}\) or \(-P_{\ast}< P(t)<0\), and \(\dot{P}(t)>0\) holds when \(0< P(t)< P_{\ast}\) or \(P(t)<-P_{\ast}\). Therefore, the ordinary differential equation (5) does not have a nonconstant periodic solution. This implies that system (2) has no τ-periodic solution. The proof is complete. □

We then have the following theorem about the global existence of a Hopf bifurcation.

Theorem 2

Suppose that \(a>bc\), \(\beta>\alpha\), and m and n are even. Then, for each \(\tau>\tau_{k}\), \(k=0,1,2,\ldots\) , system (2) still has positive periodic solutions.

Proof

For the convenience of using the results from [13], we rewrite (2) as the following functional differential equation:

$$ \dot{x}(t)=F(x_{t},\tau,p), $$
(6)

which satisfies the conditions (A1)-(A3) in [13]. Following the notations there, we have the following:

$$\varDelta _{(x_{0},\tau,p)}(\lambda)=\lambda+\alpha+\beta e^{-\lambda\tau}. $$

Here \(x_{0}\) is the equilibrium of (6). It is easy to verify that \((x_{0}, \tau_{k}, 2\pi/\omega_{0})\) are isolated centers. Then there exist \(\varepsilon>0\), \(\delta>0\) and a smooth function \(\lambda: (\tau_{j}-\delta,\tau_{j}+\delta)\rightarrow \mathbf{C}\) such that

$$\varDelta \bigl(\lambda(\tau)\bigr)=0,\qquad \bigl\vert \lambda(\tau)-i \omega_{0}\bigr\vert < \varepsilon $$

for any \(\tau\in[\tau_{k}-\delta,\tau_{k}+\delta]\), and

$$\lambda(\tau_{k})=i\omega_{0},\qquad \frac{\mathrm{d}\operatorname{Re}(\lambda(\tau))}{\mathrm{d}\tau}>0. $$

Define that \(p_{0}=2\pi/\omega_{0}\) and \(\varOmega _{\varepsilon,p_{0}}=\{ (0,p):0< u<\varepsilon,|p-p_{0}|<\varepsilon\}\). If \(|\tau-\tau_{k}|\leq\delta\) and \((u,p)\in\partial \varOmega _{\varepsilon}\), then \(\varDelta _{(x_{0},\tau,p)}(u+2\pi i/p)=0\) if and only if \(\tau=\tau_{k}\), \(u=0\), \(p=p_{k}\). Thus, assumption (A4) in [13] holds.

Next introducing a function defined by

$$H^{\pm}(x_{0},\tau_{k},2\pi/\omega_{0}) (u,p)=\varDelta _{(x_{0}, \tau_{k}\pm\delta, p)}(u+2\pi i/p) $$

yields the crossing number

$$\begin{aligned} \begin{aligned} \gamma(x_{0},\tau_{j},2\pi/\omega_{0})={}& \operatorname{deg}_{B}\bigl(H^{-}(x_{0},\tau_{k},2 \pi /\omega_{0}),\varOmega _{\varepsilon,p_{0}}\bigr) \\ &{}-\operatorname{deg}_{B}\bigl(H^{+}(x_{0}, \tau_{k},2\pi/\omega_{0}),\varOmega _{\varepsilon ,p_{0}}\bigr) \\ ={}&-1. \end{aligned} \end{aligned}$$

Thus the connected component \(\mathbb{C}(x_{0},\tau_{k},2\pi/\omega_{0})\) through \((x_{0}, \tau_{k}, 2\pi/\omega_{0})\) is nonempty, and

$$\sum_{(x_{0},\tau,p)\in\mathbb{C}(x_{0},\tau_{k},2\pi/\omega_{0})}\gamma (x_{0},\tau,p)< 0, $$

which implies that \(\mathbb{C}(x_{0},\tau_{k},2\pi/\omega_{0})\) is unbounded. From Lemmas 2 and 3, we know that the projection of \(\mathbb{C}(x_{0},\tau _{k},2\pi/\omega_{0})\) onto the x-space is bounded and that onto the τ-space is away from zero.

For a contradiction, we suppose that the projection of \(\mathbb {C}(x_{0},\tau_{k},2\pi/\omega_{0})\) onto τ-space is bounded. This means that the projection of \(\mathbb{C}(x_{0},\tau_{k},2\pi/\omega_{0})\) onto τ-space is included in an interval \((0, \tau^{\ast})\).

From the definition of \(\tau_{k}\) in Section 2, we can get that

$$\frac{\pi}{2}< \omega_{0}\tau_{0}< \pi, \quad \mbox{and} \quad 2k\pi< \omega_{0}\tau _{k}< (2k+1)\pi< 2(k+1) \pi,\quad k\geq1. $$

Hence,

$$2\tau_{0}< \frac{2\pi}{\omega_{0}}< 4\tau_{0},\quad \mbox{and} \quad \frac{\tau _{k}}{k+1}< \frac{2\pi}{\omega_{0}}< \frac{\tau_{k}}{k}, \quad k\geq1, $$

and we have \(2\tau_{0}< p<4\tau_{0}\) if \((x(t), \tau, p) \in\mathbb {C}(x_{0},\tau_{0},2\pi/\omega_{0})\), \(\tau_{1}/2< p<\tau_{1}\) if \((x(t), \tau, p) \in\mathbb{C}(x_{0},\tau_{1},2\pi/\omega_{0})\), and \(\tau_{2}/3< p<\tau_{2}/2\) if \((x(t), \tau, p) \in\mathbb{C}(x_{0},\tau_{2},2\pi/\omega_{0})\), and so on. This implies that the projection of \(\mathbb{C}(x_{0},\tau_{k},2\pi/\omega_{0})\) onto p-space is bounded. As a result, we can determine that the connected component \(\mathbb {C}(x_{0},\tau_{k},2\pi/\omega_{0})\) is bounded. This leads to a contradiction and the proof is complete. □

4 Numerical examples

To support the theoretical analysis, we consider the following system:

$$ P'(t)=P(t) \biggl(\frac{0.5}{0.75+P^{10}(t)}- \frac{0.5P^{20}(t-\tau )}{0.5+P^{20}(t-\tau)} \biggr). $$
(7)

Through a direct computation, we can determine \(P_{\ast}=0.988012\), \(\alpha=1.65509\), \(\beta=2.37657\), \(\omega_{0}=1.70551\) and \(\tau_{k}=\frac {2.34119+2k\pi}{1.70551}\), \(\tau_{0}=1.37272\), \(\tau_{1}=5.05677\), \(\tau_{2}=8.74082\), \(\tau _{3}=12.4249\), … .

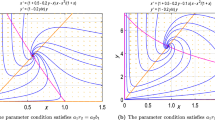
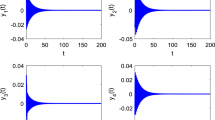
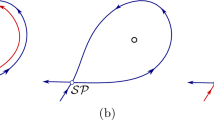
From Figures 1 and 2, we can find that a Hopf bifurcation occurs when time delay τ increases through the first critical value \(\tau_{0}\). In other words, the positive equilibrium is asymptotically stable when the time delay is small, and the periodic solution bifurcates from the positive equilibrium when the time delay is slightly larger than the first critical value. Because the conditions of Theorem 2 are satisfied, bifurcating periodic solutions exist even if the time delay is sufficiently large (see Figures 3 and 4). From these figures, we can see that time delay has a major impact on the dynamics of commodity market model (2). We can also find that the amplitude and period of the periodic solution will increase gradually as time delay increases.

Figure 1
figure 1

The equilibrium \(\pmb{P_{\ast}}\) is stable when \(\pmb{\tau =0.8<\tau_{0}}\) .

Full size image
Figure 2
figure 2

Periodic solution occurs when \(\pmb{\tau=2>\tau_{0}}\) .

Full size image
Figure 3
figure 3

Periodic solution exists when \(\pmb{\tau=10>\tau_{2}}\) .

Full size image
Figure 4
figure 4

Periodic solution still exists when \(\pmb{\tau=35>\tau_{9}}\) .

Full size image

Thus, our theoretical results and numerical simulations show that the time delay has a substantial effect on the periodic dynamic behaviors in commodity market model (2).

5 Conclusions

This paper presents the results of an investigation into the existence of local and global Hopf bifurcations for a price adjusting model with time delay. It can be concluded that time delay may destabilize the equilibrium of that model and induce periodic oscillations. Moreover, the periodic oscillations will persist even when the delay is sufficiently large, which indicates the global existence of a Hopf bifurcation in the model. Thus, the results obtained here can supplement the previous literature and help people to understand price fluctuation mechanisms.

However, from another perspective, we sometimes need to control commodity price fluctuations, and one effective method is to shorten the time between the initiation of changes in production and the final alteration of supply. More specifically, the finite delay τ is the time between production and price changes. As we know, large delay may induce complex dynamical behaviors, such as drastic periodic fluctuations. Therefore, timely price adjustments are necessary, which can effectively reduce the time delay. Mathematically, we should stabilize the positive equilibrium and control the Hopf bifurcation, and we will consider this in our work in the near future.