Abstract
Background
Sporozoites isolated from the salivary glands of Plasmodium-infected mosquitoes are a prerequisite for several basic and pre-clinical applications. Although salivary glands are pooled to maximize sporozoite recovery, insufficient yields pose logistical and analytical hurdles; thus, predicting yields prior to isolation would be valuable. Preceding oocyst densities in the midgut is an obvious candidate. However, it is unclear whether current understanding of its relationship with sporozoite densities can be used to maximize yields, or whether it can capture the potential density-dependence in rates of sporozoite invasion of the salivary glands.
Methods
This study presents a retrospective analysis of Anopheles stephensi mosquitoes infected with two strains of the rodent-specific Plasmodium berghei. Mean oocyst densities were estimated in the midguts earlier in the infection (11–15 days post-blood meal), with sporozoites pooled from the salivary glands later in the infection (17–29 days). Generalized linear mixed effects models were used to determine if (1) mean oocyst densities can predict sporozoite yields from pooled salivary glands, (2) whether these densities can capture differences in rates of sporozoite invasion of salivary glands, and (3), if the interaction between oocyst densities and time could be leveraged to boost overall yields.
Results
The non-linear effect of mean oocyst densities confirmed the role of density-dependent constraints in limiting yields beyond certain oocyst densities. Irrespective of oocyst densities however, the continued invasion of salivary glands by the sporozoites boosted recoveries over time (17–29 days post-blood meal) for either parasite strain.
Conclusions
Sporozoite invasion of the salivary glands over time can be leveraged to maximize yields for P. berghei. In general, however, invasion of the salivary glands over time is a critical fitness determinant for all Plasmodium species (extrinsic incubation period, EIP). Thus, delaying sporozoite collection could, in principle, substantially reduce dissection effort for any parasite within the genus, with the results also alluding to the potential for changes in sporozoites densities over time to modify infectivity for the next host.
Similar content being viewed by others
Background
Preventing sporozoite establishment in the human liver has been a cornerstone of anti-malarial therapies for more than a century [1]. While the RTS/S vaccine underscored the potential for targeting the most devastating of human malaria, Plasmodium falciparum, its limited efficacy served as a reminder of the need for continual improvements to the vaccine design pipeline. Sporozoites isolated from the salivary glands of mosquitoes infected with human or rodent Plasmodium species offer several benefits that are either not possible, or difficult to assess with mosquito challenge models. Indeed, isolated sporozoites have served as starting points for identifying novel mechanisms of host-parasite interactions and developing pre-clinical assays for evaluating drugs and vaccines [2,3,4,5,6,7,8,9,10,11,12]. Developing approaches to maximize sporozoite yields from the salivary glands would help streamline existing workflows [13].
Despite the benefits of working with purified sporozoites, isolating sporozoites is a labour- and technique-intensive endeavour [2, 14]. The limited carrying capacity of salivary glands requires isolating sporozoites from large pools of salivary glands dissected from multiple mosquitoes [2,3,4,5,6,7,8,9,10,11,12]. However, low sporozoite yields present a hurdle to the design, execution, and interpretation of most assays. For instance, low yields may compel a researcher to reduce the number of study groups and/or replicates on an ad hoc basis at the cost of assay throughput and statistical power. Alternatively, yields could be fortified by dissecting more salivary glands, although low infection status and/or sporozoite densities in individuals may counter any net benefits gained from increasing dissection efforts. The ability to predict sporozoite yields a priori would be useful in overcoming these limitations. Following ingestion, parasites penetrate the mosquito midgut before establishing as oocysts, lining the epithelium under the basal lamina. Sporozoite replication is initiated in the oocysts from where they are released into the hemocoel before migrating to the salivary glands, ready for injection into another host. One commonly suggested predictor of sporozoite densities in the salivary glands is the density of oocysts in the midgut, where sporozoite replication occurs. Identifying a relationship between oocyst density and sporozoite yield would be beneficial as quantifying oocyst requires relatively little investment in labour and expertise [15, 16].
Previous studies investigating relationships between oocyst and sporozoite densities suggest the relationship is non-linear, with increasing oocyst densities generally associated with diminishing returns in sporozoite yields, likely due to density-dependent constraints on sporozoite production. These constraints could involve bottom-up and top-down processes limiting sporozoite production, such as increased competition for host resources, immune activation, or vector mortality [17,18,19,20,21,22]. Density-dependent effects on sporozoite replication could also have implications for the extrinsic incubation period (EIP) or the average time it takes for sporozoites to establish in the salivary glands. While differences in EIP are critical to Plasmodium fitness in general [23, 24], the potential for density-dependent asynchronicity in the dynamics of sporozoite migration is also supported by ecological theory, which documents similar density-dependent effects on the population growth rates of other organisms [25, 26]. In fact, changes in EIP with oocyst density might explain the lack of consensus in the literature regarding when (day post–blood meal) to recover Plasmodium berghei sporozoites, with times cited ranging from as early as 17 days to 29 days post–blood meal [2, 5, 17,18,19, 21, 27,28,29,30,31,32,33,34,35,36,37,38]. Thus, by accounting for shifts in the temporal dynamics of sporozoite invasion due to variation in oocyst burdens, the current study was undertaken to test the assumption that oocyst densities would predict optimal sporozoite yields.
Since its initial demonstration [39], mosquitoes infected with the rodent–specific P. berghei constitute an important component of the vaccine and drug discovery pipeline, with sporozoite yields from the salivary glands a critical bottleneck for several downstream applications [2]. Results described herein represent a retrospective, statistical analysis of a dataset consisting of 46 groups of mosquitoes infected with either one of the two strains of P. berghei, with the objective of asking the following questions: (1) how does oocyst density affect overall sporozoite yields, (2) can oocyst density predict rates of sporozoite migration, and (3) can this interaction be used to optimize sporozoite yields? Oocyst densities were estimated once between 11 and 15 days post-blood meal from a subgroup of individuals’ midguts, with sporozoites pooled from the salivary glands of another subgroup at one to four time points between 17 and 29 days post-blood meal (Additional file 3: Table S1). Sporozoite yields were then modelled with the (arithmetic) mean oocyst densities estimated earlier in the infection to determine whether yields were also dependent on time and/or parasite strain. The models were used to test the hypothesis that as oocyst densities increase, delayed replication and/or migration of sporozoites will enhance sporozoite yields over time, before eventually saturating and/or declining for both parasite strains. Analysis indicates that irrespective of parasite strain, sporozoite yields from pooled salivary glands were dependent on a non-linear relationship with the mean oocyst densities. In addition, sporozoite migration over the 17–29-day sampling period facilitated a linear increase in yields, albeit independent of the mean oocyst densities. Taken together, this study suggests sporozoite yields could be streamlined further by leveraging the dynamics of sporozoite migration. Finally, at the oocyst densities tested here, density-dependent migration may yet be the primary reason for increased sporozoite yields, although pooling salivary glands may only provide a qualitative overview of how sporozoite yields change over time; in other words, the rates of migration are likely to vary quantitatively between individuals, especially at oocyst densities where these rates could be used to maximize yields.
Methods
Chemical and consumables
Unless stated otherwise, all chemicals and consumables were purchased from Thermo Scientific Inc. (Hampton, NY).
Parasite strains
Mice were infected with one of the two parasite strains, P. berghei WT (clone ANKA, referred to hereon as PbANKA, kind gift from Dr. Evlina Angov, Walter Reed Army Institute of Research, Silver Spring, MD), or a transgenic strain of P. berghei. Transgenic parasites were generated in female OF1 mice (6–7 weeks; Charles River, NL) in accordance with the European Guideline 86/609/EEC and follow the FELASA (Federation of European Laboratory Animal Science Associations) guidelines and recommendations concerning laboratory animal welfare. Animal experiments performed in Leiden University Medical Center (LUMC, Leiden, The Netherlands) were approved by the Animal Experiments Committee of the Leiden University Medical Centre (DEC 10099).
To generate the reporter line, GFP-Lucama1-eef1a, the reference clone cl15cy1 of the P. berghei ANKA strain was used [40]. Two GFP-Luciferase expression cassettes were inserted into the neutral p230p gene locus (PBANKA_0306000) using standard transfection technologies (Additional file 1: Fig. S1a) [40]. To generate DNA construct pL1308, two standard DNA constructs were used, pL1063 [41, 42] and pL1156 [43]. The eef1a-GFP-Luc expression cassette of pL1063 (SacI fragment) was cloned into the SacI site of pL1165, generating plasmid pL1308 that contains the two gfp-luc fusion genes under the control of the eef1a (PBANKA_1133300) promoter or the ama1 (PBANKA_0915000) promoter, respectively, and contains the two 5′ and 3′ p230p target regions (TR). The construct was linearized using SacII restriction sites outside of the 5′ and 3′ p230p TR before transfection. After transfection (exp. 1052), transfected parasites were obtained by flow-sorting based on GFP expression as described [41, 42], followed by cloning using the method of limiting dilution [40], resulting in line GFP-Lucama1-eef1a (line 1052cl1). Correct integration of DNA construct into the genome of GFP-Lucama1-eef1a was confirmed by Southern analyses of Pulsed Field Gel (PFG)-separated chromosomes (Additional file 1: Fig. S1b) [40]. PFG-separated chromosomes were hybridized with the 3’utr Pbdhfr/ts probe [40].
Mice infections
All procedures described herein were approved by the University of Georgia’s Institutional Animal Care and Use Committee GA under Animal Use Protocol number A2016 06-010-Y1-A0 and A2020 01-013-Y2-A3. Three to 4 days before mosquito feeds, female C57BL/6 mice or Hsd:ICR(CD-1) mice (Envigo, Indianapolis, IN), aged 6–8 weeks, were injected intraperitoneally with 500 µL parasite suspended in sterile PBS with a density of 5 × 106 or 107 parasites per mouse with either P. berghei ANKA or the GFP-luciferase expressing strain of P. berghei (GFP-Lucama1-eef1a, referred to herein as PbGFP-LUCCON). Total parasitaemia (trophozoites, schizonts, and gametocytes) was estimated starting 2 days post-infection with a Giemsa-stained smear of 1–2 µL of blood collected from the tail vein of each mouse [44]. Once total parasitaemia had reached 2–6% (usually 4 days), each mouse was anesthetized with ~ 0.5 ml of 1.25% 2,2,2-Tribromoethanol (v/v, Avertin, Sigma-Aldrich) and placed atop mosquito cages.
Mosquito infections with P. berghei infected mice
Anopheles stephensi colonies were maintained as described previously, with adult mosquitoes maintained on a diet of 5% dextrose (w/v) and 0.05% para-aminobenzoic acid (w/v), a constant temperature of 27 °C and relative humidity of 75–85%, on a 12 h day/night cycle [44, 45]. Infections were performed with 3- to 7–day old, host-seeking female An. stephensi sorted into cages (17.5 cm L × 17.5 cm W × 17.5 cm H, BugDorm Inc., Taiwan). Approximately 24 h prior to infections, mosquitoes were transferred to a 20 °C chamber (Percival Scientific Inc., Dallas, IA) and starved before being fed on anesthetized mice for 15–20 min.
Measuring oocyst densities in the midguts and sporozoite isolations
For quantifying oocyst densities in the midguts, mosquitoes from each group were vacuum aspirated directly into 70% ethanol, washed twice with ice-cold PBS, and oocysts enumerated as described previously [44, 45]. Salivary glands from mosquitoes in each group were used to isolate sporozoites, as described previously, with modifications [46]. Mosquitoes were first transferred to 16–ounce paper cups and cold anesthetized at – 20 °C for two to three minutes. Anesthetized mosquitoes were then transferred to a sterile petri dish (10 cm) maintained at − 2 to – 4 °C on a portable chill table (BioQuip Products, Rancho Dominguez, CA). Mosquitoes were surface sterilized with 70% ethanol before being dissected in chilled, sterile Schneider 2 (S2) insect cell culture media supplemented with 0.1% (v/v) fetal bovine serum. Using a tungsten micro–dissecting needle (0.25 mm diameter, 1 µm tip, Roboz Surgical Instrument Co., Gaithersburg, MD), salivary glands were pooled in a 1.5 ml microcentrifuge tube containing 100–500 µL of the dissection media; care was taken to ensure all six lobes were accounted for. Pooled glands were then disrupted with 5–10 passages through a sterile, 30G needle (Becton–Dickinson, Franklin Lakes, NJ) to release sporozoites [5]. Sporozoites were counted in a 10 μL aliquot with a haemocytometer and total yields were expressed as follows.
where Y denotes sporozoite yields, m indicates mean sporozoites counted from the four corner grids in a volume of 0.1 μL, with a constant of ‘10’ to further express ‘m’ per μL (i.e., 0.1 × 10 = 1 μL), and v indicates original volume of sporozoite suspension that the aliquot was drawn from (e.g., 500 μL). To express yields per mosquito, the following equation was used.
where y denotes sporozoite yields per mosquito, Y indicates total sporozoite yields (from Eq. 1 above), with n representing the number of salivary glands pooled initially.
Data analyses and statistical modelling
The dataset used in the current study represents 46 groups of P. berghei-infected mosquitoes, of which 36 were infected with P. berghei ANKA and the remaining 10 with PbGFP-LUCCON. Each group comprised 70–200 mosquitoes, distinguished based on being exposed to the same mouse (i.e., the same source of infection). Time of sampling was replicated over the 46 independent groups in a cross-sectional/partially nested sampling schedule where, for instance, sporozoite yields at 26 days post-blood meal were replicated across groups 4, 5, 17, 20, 27, 38, and 45 (Additional file 3: Table S1) [47, 48]. To accommodate the imbalanced nature of data collection, generalized linear mixed-effects models (GLMMs) were used to test hypotheses [47,48,49,50], with slopes of sporozoite yields dependent on the fixed effects/predictors (averaged oocyst densities, time, and/or parasite strain), but with intercepts allowed to vary randomly among the 46 groups (“fixed slopes, random intercepts”). Specifying groups as a random effect allows for the possibility that the relationship between oocyst and sporozoite densities measured in different individuals (since a mosquito can either be sampled for oocysts or sporozoites [2]) may show a greater correlation between mosquitoes that were exposed to the same source of infection (i.e., the same mouse) [18, 19, 21].
All data analyses and modelling were performed in RStudio [51], an integrated development environment for the open-source R package (version 4.1.0) [52], and associated packages. Graphical analyses were performed with the “ggplot2” package (version 3.3.5) [53] with the number of sporozoites recovered displayed as yields per mosquito (i.e., y from Eq. 2 above, rounded to the nearest integer). Because pooling prevents the estimation of each individual’s contribution of sporozoites, this method of expression does not represent a “true” average [54]. GLMMs were specified as suggested by the “glmmTMB” package [50]. Dispersion characteristics of residuals were tested in the “DHARMa” package (version 0.4.3). Tables were prepared for presentation with the “sjPlot” package (version 2.8.9) [55].
To maintain consistency with studies that rely on pooled sporozoites [2, 5, 17,18,19, 21, 27,28,29,30,31,32,33,34,35,36,37,38], statistical modelling was performed with sporozoite yields per mosquito (i.e., y from Eq. 2 above) specified as the dependent variable (model referred to herein as the ‘default’ model). However, to determine if differences in the number of salivary glands can alter model fit, a second model was built with total sporozoite yields expressed as the dependent variable (i.e., Y from Eq. 1 above), but with the number of salivary glands pooled added as an offset (n from Eq. 2 above) (model referred to herein as the ‘offset’ model). For instance, if 243,000 sporozoites were recovered from 31 mosquitoes, the dependent variable (y) in the ‘default model would be 7839 (or the quotient of 243,000/31, rounded to the nearest integer); the dependent variable in the ‘offset’ model would be 243,000, with the number of salivary glands dissected (i.e., 31) included as an ‘offset’ to account for differences in the number of salivary glands pooled between groups and/or time points [50]. Note that neither method of expression is based on true averages and thus, the ‘mean’ predicted by the statistical analysis should also not be considered a ‘true’ mean [55]. In addition, because of the distinct dependent variables, it was not possible to compare their fits with likelihood-based criteria [50].
Of the three fixed effects, parasite strain was coded as a categorical variable, while averaged oocyst densities and days post-blood meal were specified as continuous variables and centred and scaled with the mean and standard deviations, respectively [45]. Averaged oocyst densities were estimated by deriving the arithmetic mean of oocyst densities in all midguts, irrespective of infection status (i.e., midguts with oocysts ≥ 0). Expressing oocyst densities as the arithmetic mean was in keeping with how sporozoite yields were expressed, which, despite not being a true average, is more similar to how the arithmetic means (y in Eq. 2 above) are expressed, compared to other representations of central tendency [54]. Although only oocyst-positive mosquitoes will contribute to the sporozoite pool, our rationale for including all midguts irrespective of infection status is because salivary glands are generally dissected from all available mosquitoes irrespective of infection status (e.g., [2]).
In general, both ‘default’ and ‘offset’ models included sporozoite yields as a linear function of averaged oocyst densities, days post-blood meal (i.e., time), and parasite strain as main effects, and up to a three-way interaction. While a clear interaction between the three predictors would indicate differences between strains, a clear two-way interaction between oocyst densities and time on sporozoite density in the salivary glands would be indicative of density-dependence in sporozoite migration. To test the potential for saturation and decline in sporozoite yields due to mean oocyst densities and/or time (i.e., to model the hump-shaped effect on yields [45]), quadratic terms (or second-order polynomial) of the two predictors were also considered as additive (main) effects. However, in keeping with the objective of describing a simple predictive framework, automated stepwise elimination (based on likelihood-ratio tests and Akaike’s information criteria, corrected for small sample sizes (ΔAICc)) was used to identify the most parsimonious combination of predictors (predictors with p < 0.05) from either the ‘default’ or ‘offset’ models described above (referred to herein as ‘minimal’ models) [50]; note that distinct dependent variables meant direct statistical comparisons (using likelihood-based criteria) could not be performed ‘default’ and ‘offset’ models (either full or minimal) [50]. However, to enable indirect comparison, all visual displays of model fits were based on the minimal versions of ‘default’ and ‘offset’ models, with predicted means and 95% confidence intervals (95%CI) expressed per mosquito; predictions were derived via post-hoc simulations, as specified in the “ggeffects” package (version 1.1.1) [55].
Results
Summary of data
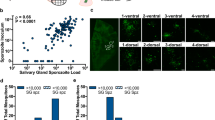
The results are based on data from 2557 mosquitoes. Between 11 and 15 days post–blood meal, oocyst densities were quantified once from mosquitoes infected with P. berghei ANKA or PbGFP-LUCCON (Additional file 4: Table S2). Starting 17 days post-blood meal, salivary glands from either a subsample or all remaining individuals were pooled to isolate sporozoites at one to four time points until 29 days post-blood meal (Fig. 1 and Additional file 3: Table S1). In general, heterogeneity (or differences) in oocyst densities between individuals, represented by the standard deviations, increased linearly with the corresponding mean for the 46 groups of mosquitoes (Pearson’s r (95%CI) = 0.88 (0.79–0.93), p < 0.001) (Fig. 2).
Sporozoite yields increase (a) non-linearly with (arithmetic) mean oocyst densities earlier in the infection (11–15 days post-blood meal), and (b) linearly over time (17–29 days post-blood meal) for mosquitoes infected with P. berghei strains PbANKA (circles) or PbGFP-LUCCON (triangles). Lines and shaded areas indicate the mean and uncertainty (95% CI), respectively, predicted by the minimal model (Table 1). Mean oocyst densities were derived from counts of individual midguts, irrespective of infection status (oocysts ≥ 0). Note that although sporozoite yields are expressed per mosquito, values do not represent a true mean as counts are from pooled salivary glands, with no information of densities contributed by individuals
Mean oocyst densities for the 46 groups of mosquitoes increase linearly with the respective standard deviations (orange crosses), indicating the potential for collecting sporozoites from individuals with increasingly heterogeneous oocyst densities. Mosquitoes were infected with P. berghei strains PbANKA (circles) or PbGFP-LUCCON (triangles)
Sporozoite yields increase non-linearly with mean oocyst densities, and linearly over time
The full model (Table 1) suggested sporozoite yields (y in Eq. 2) were driven by a non-linear relationship with the (arithmetic) mean of oocyst densities estimated earlier in the infection: the initial increase in yields (‘linear’, Z-value = 5.52, p < 0.001, Table 1) was eventually followed by a decline (‘quadratic’, Z-value = − 2.22, p = 0.027, Table 1) (Fig. 1a). Although the model was unable to identify a clear interaction between mean oocyst densities and time (Z-value = − 1.01, p = 0.312, Table 1), it suggested a relatively weaker (vs. oocyst densities), yet positive, linear effect of time on yields (Z-value = 2.62, p = 0.009, Table 1); in other words, at all mean oocyst densities tested here, the sporozoite migration dynamic resulted in higher sporozoite yields over time (Fig. 1b). Unlike the non-linear effect of mean oocyst densities (‘quadratic’), the model suggested yields did not decline with time post-infection (‘quadratic’, Z-value = 0.49, p = 0.623, Table 1). Additionally, the influence of mean oocyst densities and time on sporozoite yields did not differ between parasite strains (PbANKA or PbGFP-LUCCON) (rows 6, 8, 9, and 10, Table 1).
While mean oocyst densities and time were able to explain 47.6% of the variation in the dataset (Marginal R2, Table 1), allowing random variation among groups in the contribution of these predictors improved the model’s account of the overall variation in the dataset (Conditional R2 = 77.7%, Table 1). Excluding group as a random effect significantly worsened model fit (ΔAICc = + 13.2). Finally, stepwise elimination of the least significant predictors from the full model (‘Minimal model’, Table 1) confirmed the non-linear effects of mean oocyst densities (‘linear’, Z-value = 6.17, p < 0.001 and ‘quadratic’, Z-value = − 2.83, p = 0.005) and time of sporozoite collection (i.e., days post-blood meal) were sufficient to model the overall trends (‘linear’, Z-value = 2.73, p = 0.006).
Sporozoite yields increase with time, irrespective of how many salivary glands were pooled
In general, both the ‘default’ (Table 1) and ‘offset’ models (Additional file 5: Table S3) were consistent in highlighting the contribution of mean oocyst densities and time (rows 2, 3, and 4, Table 1 and Additional file 5: Table S3, differences in model structure are explained in ‘Data analyses and statistical modelling’ section). Sporozoite yields simulated over the same parameters for both models were also similar (Fig. 3); specifically, sporozoite yields increased with mean oocyst densities and time (colored lines), albeit with a corresponding increase in uncertainty (shaded areas, Fig. 3).
Predicted sporozoite yields over time (17, 24, and 29 days post-blood meal) at the respective mean oocyst densities (x-axis). Predictions after modelling sporozoite yields as (a) the ‘mean’ (minimal model of ‘default model’, Table 1) or (b) after considering differences in the number of salivary glands (minimal model of ‘offset model’, Additional file 5: Table S3). Lines and shaded areas indicate the mean and uncertainty (95%CI), respectively
Discussion
While mean oocyst densities estimated earlier in the infection were able to capture the non-linear trends in sporozoite recovery, the continued migration of sporozoites to the salivary glands also resulted in higher sporozoite yields over 17–29 days post-blood meal. The effect of mean oocyst densities and time were independent of parasite strain, and the number of salivary glands pooled, further suggesting that the effects described here should be broadly applicable. Taking the results together, this study describes a framework where mean oocyst densities estimated earlier in the infection could be used to approximate yields a priori, with the potential for yields to be maximized by leveraging the relationship between sporozoite yields and time. For example, at all mean oocyst densities, the ‘default’ model suggested that compared to 17 days post-blood meal, yields may be 1.3-, 1.7-, and 2.2-fold higher at 21, 25, and 29 days post-blood meal, respectively (Fig. 3). While yields will be dependent on mean oocyst densities, in general, accounting for the effect of time offer several benefits such as dissecting fewer mosquitoes, increasing the efficiency of otherwise cumbersome technical procedures, and potentially providing more reliability to downstream assays.
The range of sporozoites reported here generally corroborates previous findings from individual or pooled mosquitoes infected with P. berghei [17,18,19, 21, 33,34,35,36,37,38, 56,57,58,59,60]. The quadratic effect of mean oocyst densities on sporozoite yields increased with mean oocyst densities in a non-linear manner, wherein the initial increase in yields until ~ 50 oocysts were followed by a decline. In general, this non-linearity has been noted for sporozoites produced by both rodent and human Plasmodium species; current evidence suggests sporozoite densities may be dependent on complex interactions between nutritional availability, vector mortality, and immune responses to the oocysts and/or sporozoites [22, 61,62,63]. For P. berghei, the decline in sporozoite densities was noted at mean oocyst densities ≥ 50 per midgut [19, 21], with at least one study suggesting vector mortality during sporozoite egress as the most likely explanation for the reduced recovery [21]. A major benefit of this analysis is that the relationship between sporozoite yields and time post-infection can now be leveraged to reduce the risk of losing sporozoites at high mean oocyst densities (e.g., > 50) [19, 21], while also reducing dissection effort by boosting yields at lower oocyst densities. Although the model was unable to detect any evidence of a density-dependent delay (lack of clear association between mean oocyst densities and time), the clear effect of time suggested that the continued invasion of salivary glands should still be beneficial to sporozoite yields. Taken together, the effects of oocyst densities and time carry two implications for maximizing sporozoite yields. First, the non-linear effect of mean oocyst densities suggests that as oocyst densities increase (> 50), more mosquitoes would need to be dissected to obtain yields comparable to groups with lower densities. Second, although yields may increase linearly over time for all oocyst densities, groups with mean oocyst densities over 50 may still yield more sporozoites than groups with oocyst densities under 50, even if, for instance, sporozoite collection was delayed to 29 days post-blood meal (Fig. 3).
In addition to testing the potential for yields to decline with increasing mean oocyst densities (≥ 50), both models also tested whether yields would decline over time, by including a quadratic (“humped”) effect of days post-blood meal on sporozoite yields (Additional file 4: Table S2 and Additional file 5: Table S3). While the model was unable to identify a time point when yields started declining, simulations based on the model fit suggested that irrespective of mean oocyst density, yields became increasingly uncertain starting ~ 25 days post-blood meal (Figs. 1b and 2). Whether this was due to a lack of data, nutritional resources, heightened immune responses, a sign of deteriorating host health and increased mortality, or sporozoite senescence [19,20,21], is not possible to ascertain here. As such, until more data is available, results from the current study suggests sampling mosquitoes at ~ 25 days post-blood meal, but no later than 29 days when sporozoite infectivity has been suggested to decline [33]. Based on the available data, the model predicts 1.7-fold higher yields at 25 days (vs 17 days), irrespective of mean oocyst densities.
Together, mean oocyst densities and time were able to account for just under 50% of the overall variation in sporozoite yields from the dataset (e.g., Table 1). Allowing the contributions of the two predictors to vary randomly among groups significantly improved the model’s account of the total variation (R2 > 70%, Table 1), indicating the presence of other confounders specific to each group contributed significantly to the variation around the predicted yields (Figs. 1 and 3). For instance, of the groups where more information was available, one potential source of variation was a group of PbANKA-infected mosquitoes, which, despite only carrying a mean of 10.1 oocysts/midgut provided unexpectedly high sporozoite yields over time. However, only seven of the 17 individuals dissected (41%) showed evidence of having fed on the mouse (presence of eggs in ovaries during oocyst quantifications, mean feeding rates for all groups ± se = 72.4% ± 2.7), suggesting that < 50% of the group could contribute to the sporozoite pool (albeit with the caveat that estimation of feeding rates may be masked by eggs being reabsorbed by the mother [64,65,66]). These seven blood-fed individuals were carrying a mean of 25 oocysts per midgut, which was higher than the 10.1 calculated earlier, but more likely to explain the higher sporozoite yields observed for the group. In contrast, a group of PbGFP-LUCCON-infected mosquitoes with a mean oocyst density of 46.2 should have yielded, according to the model, significantly more sporozoites than the 5250 recovered from 15 salivary glands (or 350 per mosquito) at 17 days post-blood meal. To determine why the yields were low, oocysts were quantified in the midguts of these 15 individuals at the time of sporozoite collections (i.e., 17 days) and found to be carrying 17 mean oocysts per midgut, which was lower than the 46.2 mean oocysts measured earlier from the same group. Whether the reduction in oocyst densities were due to excess mortality in the cage or overestimation of mean oocyst densities earlier, the low oocyst densities were the likely reason for the low yields observed. While the models identified these groups as sources of variation, in general, they were consistent with the conclusion that yields were driven by mean oocyst densities and time.
While the instances above highlight how ‘accurate’ estimation of mean oocyst densities is also critical to predicting sporozoite yields over time, despite the consistency, the effect of time on sporozoite yields was less clear (Table 1). Future experiments with sporozoites collected over a more balanced sampling schedule, and a fixed number of individuals could address some of the study limitations and offer clearer insight into whether rates of sporozoite migration do indeed vary with oocyst density. As oocyst densities increase, sporozoite migration over time may be the primary reason for increased yields (Fig. 1a), however, a clear estimation of its contribution may be confounded by pooling sporozoites from individuals with increasingly heterogenous oocyst densities (shaded areas, Additional file 2: Fig. S2).
Further, this heterogeneity between individuals in their contribution to the sporozoite pool could explain why adjusting for differences in the number of salivary glands did not identify a clearer effect of time (Additional file 5: Table S3). Thus, estimating the relationship between oocyst density and sporozoite yields from pooled salivary glands likely only provides qualitative insight into a process that may vary quantitatively among individuals. Considering this, isolating sporozoites from all mosquitoes at a single day post-blood meal (e.g., 25–26 days), instead of at fixed intervals, may be a more efficient use of mosquitoes and time, while still achieving maximal sporozoite yields.
There are two additional caveats associated with the study and analysis. First, although the main effects of mean oocyst densities and time were common to both parasite strains, the objective of this study was not to compare strains and as such, the potential for strains to differ in overall sporozoite output should not be disregarded [21]. Second, differences between mosquito colonies due to genetic (e.g., An. stephensi “Indian” vs “SDA–500”) [67, 68] and/or epigenetic effects (for instance, larval culture conditions and its carry-over effect on adults) [69], may manifest as differences in parasite infection, replication, and sporozoite yields. While these differences suggest that more careful consideration may be necessary before settling on specific (or range of) parameters, the fundamental nature of the relationship between oocyst densities, time, and sporozoite yields should be consistent.
Conclusions
As with other organismal systems, density-dependent effects in Plasmodium parasites resulted in a non-linear relationship between the density of parasites successfully establishing (oocysts) and the transmission stages (sporozoites) [23, 70]. In general, the temporal dynamics of sporozoite migration are critical to Plasmodium fitness. Thus, in addition to indicating how prior oocyst densities could be leveraged to streamline sporozoite isolations for other Plasmodium species [2], the current study highlights the potential for oocyst densities to predict when a mosquito becomes infectious (EIP), while also suggesting how changes in sporozoite densities over time can alter parasite infectivity to the next host [33, 71]. Irrespective of the downstream application, the versatility offered by rodent malaria models underscores their continued utility in evaluating strategies to manage parasite transmission, but also how these efforts can be aided by an increased understanding of fundamental aspects of vector-parasite interactions.
Availability of data and materials
Upon acceptance, all data and statistical code from the study will be posted to a public repository.
References
Goh YS, McGuire D, Renia L. Vaccination with sporozoites: models and correlates of protection. Front Immunol. 2019;10:1227.
Menard R. Malaria: methods and protocols. 2nd edition; Springer; 2013:626.
Cowell AN, Winzeler EA. Advances in omics-based methods to identify novel targets for malaria and other parasitic protozoan infections. Genome Med. 2019;11:63.
Rosenberg R, Rungsiwongse J. The number of sporozoites produced by individual malaria oocysts. Am J Trop Med Hyg. 1991;45:574–7.
Leitner WW, Bergmann-Leitner ES, Angov E. Comparison of Plasmodium berghei challenge models for the evaluation of pre-erythrocytic malaria vaccines and their effect on perceived vaccine efficacy. Malar J. 2010;9:145.
Kreutzfeld O, Muller K, Matuschewski K. Engineering of genetically arrested parasites (GAPs) for a precision malaria vaccine. Front Cell Infect Microbiol. 2017;7:198.
Kori LD, Valecha N, Anvikar AR. Insights into the early liver stage biology of Plasmodium. J Vector Borne Dis. 2018;55:9–13.
Parmar R, Patel H, Yadav N, Patidar M, Tyagi RK, Dalai SK. Route of administration of attenuated sporozoites is instrumental in rendering immunity against Plasmodia infection. Vaccine. 2016;34:3229–34.
Sauerwein RW, Bousema T. Transmission blocking malaria vaccines: assays and candidates in clinical development. Vaccine. 2015;33:7476–82.
Mordmuller B, Supan C, Sim KL, Gomez-Perez GP, Ospina Salazar CL, Held J, et al. Direct venous inoculation of Plasmodium falciparum sporozoites for controlled human malaria infection: a dose-finding trial in two centres. Malar J. 2015;14:117.
Singh N, Barnes SJ, Kennedy S, Adams JH. Experimental evaluation of cryopreservative solutions to maintain in vitro and in vivo infectivity of P. berghei sporozoites. PLoS ONE. 2017;12:e0177304.
Marques-da-Silva C, Peissig K, Kurup SP. Pre-erythrocytic vaccines against malaria. Vaccines (Basel). 2020;8:400.
WHO. World malaria report. Geneva, World Health Organization; 2021.
Schrum M, Canezin A, Chakravarty S, Laskowski M, Comert S, Sevimli Y, et al. An efficient production process for extracting salivary glands from mosquitoes. arXiv 2019.
Stone WJ, Eldering M, van Gemert GJ, Lanke KH, Grignard L, van de Vegte-Bolmer MG, et al. The relevance and applicability of oocyst prevalence as a read-out for mosquito feeding assays. Sci Rep. 2013;3:3418.
Miura K, Swihart BJ, Deng B, Zhou L, Pham TP, Diouf A, et al. Strong concordance between percent inhibition in oocyst and sporozoite intensities in a Plasmodium falciparum standard membrane-feeding assay. Parasit Vectors. 2019;12:206.
Vanderberg JP, Yoeli M. Effects of temperature on sporogonic development of Plasmodium berghei. J Parasitol. 1966;52:559–64.
Sinden RE, Dawes EJ, Alavi Y, Waldock J, Finney O, Mendoza J, et al. Progression of Plasmodium berghei through Anopheles stephensi is density-dependent. PLoS Pathog. 2007;3: e195.
Dawes EJ, Churcher TS, Zhuang S, Sinden RE, Basanez MG. Anopheles mortality is both age- and Plasmodium-density dependent: implications for malaria transmission. Malar J. 2009;8:228.
Miazgowicz KL, Shocket MS, Ryan SJ, Villena OC, Hall RJ, Owen J, et al. Age influences the thermal suitability of Plasmodium falciparum transmission in the Asian malaria vector Anopheles stephensi. Proc Biol Sci. 2020;287:20201093.
Pollitt LC, Churcher TS, Dawes EJ, Khan SM, Sajid M, Basanez MG, et al. Costs of crowding for the transmission of malaria parasites. Evol Appl. 2013;6:617–29.
Vaughan JA. Population dynamics of Plasmodium sporogony. Trends Parasitol. 2007;23:63–70.
Childs LM, Prosper OF. The impact of within-vector parasite development on the extrinsic incubation period. R Soc Open Sci. 2020;7:192173.
Ohm JR, Baldini F, Barreaux P, Lefevre T, Lynch PA, Suh E, et al. Rethinking the extrinsic incubation period of malaria parasites. Parasit Vectors. 2018;11:178.
Wilson K, Bjørnstad ON, Dobson AP, Merler S, Poglayen G, Randolph SE, et al. Heterogeneities in macroparasite infections: patterns and processes. In: Hudson PJ, Rizzoli A, Grenfell BT, Heesterbeek, editors., et al., The ecology of wildlife diseases. Oxford: Oxford University Press; 2002. p. 1–48.
Beckerman AP, Benton TG, Ranta E, Kaitala V, Lundberg P. Population dynamic consequences of delayed life-history effects. Trends Ecol Evol. 2002;17:263–9.
Tartz S, Deschermeier C, Retzlaff S, Heussler V, Sebo P, Fleischer B, et al. Plasmodium berghei sporozoite challenge of vaccinated BALB/c mice leads to the induction of humoral immunity and improved function of CD8(+) memory T cells. Eur J Immunol. 2013;43:693–704.
Gilbert SC, Schneider J, Hannan CM, Hu JT, Plebanski M, Sinden R, et al. Enhanced CD8 T cell immunogenicity and protective efficacy in a mouse malaria model using a recombinant adenoviral vaccine in heterologous prime-boost immunisation regimes. Vaccine. 2002;20:1039–45.
Sato Y, Montagna GN, Matuschewski K. Plasmodium berghei sporozoites acquire virulence and immunogenicity during mosquito hemocoel transit. Infect Immun. 2014;82:1164–72.
Vaughan JA, Scheller LF, Wirtz RA, Azad AF. Infectivity of Plasmodium berghei sporozoites delivered by intravenous inoculation versus mosquito bite: implications for sporozoite vaccine trials. Infect Immun. 1999;67:4285–9.
Nganou-Makamdop K, van Gemert GJ, Arens T, Hermsen CC, Sauerwein RW. Long term protection after immunization with P. berghei sporozoites correlates with sustained IFNgamma responses of hepatic CD8+ memory T cells. PLoS ONE. 2012;7:e36508.
Manzoni G, Marinach C, Topcu S, Briquet S, Grand M, Tolle M, et al. Plasmodium P36 determines host cell receptor usage during sporozoite invasion. Elife. 2017;6: e25903.
Coosemans M, Wery M, Van Marck E, Timperman G. Studies on the infectivity of Plasmodium berghei sporozoites in experimental hosts. Ann Soc Belg Med Trop. 1981;61:349–68.
Costa G, Gildenhard M, Eldering M, Lindquist RL, Hauser AE, Sauerwein R, et al. Non-competitive resource exploitation within mosquito shapes within-host malaria infectivity and virulence. Nat Commun. 2018;9:3474.
Choudhary HH, Gupta R, Mishra S. PKAc is not required for the preerythrocytic stages of Plasmodium berghei. Life Sci Alliance. 2019;2: e201900352.
Wang Q, Fujioka H, Nussenzweig V. Exit of Plasmodium sporozoites from oocysts is an active process that involves the circumsporozoite protein. PLoS Pathog. 2005;1: e9.
Porter MD, Nicki J, Pool CD, DeBot M, Illam RM, Brando C, et al. Transgenic parasites stably expressing full-length Plasmodium falciparum circumsporozoite protein as a model for vaccine down-selection in mice using sterile protection as an endpoint. Clin Vaccine Immunol. 2013;20:803–10.
Yang J, Schleicher TR, Dong Y, Park HB, Lan J, Cresswell P, et al. Disruption of mosGILT in Anopheles gambiae impairs ovarian development and Plasmodium infection. J Exp Med. 2020;217: e20190682.
Nussenzweig RS, Vanderberg J, Most H, Orton C. Protective immunity produced by the injection of x-irradiated sporozoites of Plasmodium berghei. Nature. 1967;216:160–2.
Janse CJ, Ramesar J, Waters AP. High-efficiency transfection and drug selection of genetically transformed blood stages of the rodent malaria parasite Plasmodium berghei. Nat Protoc. 2006;1:346–56.
Janse CJ, Franke-Fayard B, Mair GR, Ramesar J, Thiel C, Engelmann S, et al. High efficiency transfection of Plasmodium berghei facilitates novel selection procedures. Mol Biochem Parasitol. 2006;145:60–70.
Janse CJ, Franke-Fayard B, Waters AP. Selection by flow-sorting of genetically transformed, GFP-expressing blood stages of the rodent malaria parasite, Plasmodium berghei. Nat Protoc. 2006;1:614–23.
Fonager J, Pasini EM, Braks JA, Klop O, Ramesar J, Remarque EJ, et al. Reduced CD36-dependent tissue sequestration of Plasmodium-infected erythrocytes is detrimental to malaria parasite growth in vivo. J Exp Med. 2012;209:93–107.
Pathak AK, Shiau JC, Thomas MB, Murdock CC. Cryogenically preserved RBCs support gametocytogenesis of Plasmodium falciparum in vitro and gametogenesis in mosquitoes. Malar J. 2018;17:457.
Pathak AK, Shiau JC, Thomas MB, Murdock CC. Field relevant variation in ambient temperature modifies density-dependent establishment of Plasmodium falciparum gametocytes in mosquitoes. Front Microbiol. 2019;10:2651.
Schmid MA, Kauffman E, Payne A, Harris E, Kramer LD. Preparation of mosquito salivary gland extract and intradermal inoculation of mice. Bio Protoc. 2017;7: e2407.
Schielzeth H, Nakagawa S. Nested by design: model fitting and interpretation in a mixed model era. Methods Ecol Evol. 2013;4:14–24.
Harrison XA, Donaldson L, Correa-Cano ME, Evans J, Fisher DN, Goodwin CED, et al. A brief introduction to mixed effects modelling and multi-model inference in ecology. PeerJ. 2018;6: e4794.
Silk MJ, Harrison XA, Hodgson DJ. Perils and pitfalls of mixed-effects regression models in biology. PeerJ. 2020;8: e9522.
Brooks ME, Kristensen K, van Benthem KJ, Magnusson A, Berg CW, Nielsen A, et al. glmmTMB balances speed and flexibility among packages for zero-inflated generalized linear mixed modeling. R J. 2017;9:378–400.
RStudio Team. RStudio: Integrated Development Environment for R. Boston, MA: RStudio, Inc.; 2016.
R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2018.
Wickham H. ggplot2: elegant graphics for data analysis. New York: Springer-Verlag; 2016.
Manikandan S. Measures of central tendency: the mean. J Pharmacol Pharmacother. 2011;2:140–2.
Lüdecke D. strengejacke: Load Packages Associated with Strenge Jacke!, R package version 0.3.0 edition2018.
Armistead JS, Jennison C, O’Neill MT, Lopaticki S, Liehl P, Hanson KK, et al. Plasmodium falciparum subtilisin-like ookinete protein SOPT plays an important and conserved role during ookinete infection of the Anopheles stephensi midgut. Mol Microbiol. 2018;109:458–73.
Siden-Kiamos I, Pace T, Klonizakis A, Nardini M, Garcia CRS, Curra C. Identification of Plasmodium berghei Oocyst Rupture Protein 2 (ORP2) domains involved in sporozoite egress from the oocyst. Int J Parasitol. 2018;48:1127–36.
Saeed S, Tremp AZ, Dessens JT. The Plasmodium LAP complex affects crystalloid biogenesis and oocyst cell division. Int J Parasitol. 2018;48:1073–8.
Ukegbu CV, Giorgalli M, Tapanelli S, Rona LDP, Jaye A, Wyer C, et al. PIMMS43 is required for malaria parasite immune evasion and sporogonic development in the mosquito vector. Proc Natl Acad Sci USA. 2020;117:7363–73.
Hollin T, De Witte C, Freville A, Guerrera IC, Chhuon C, Saliou JM, et al. Essential role of GEXP15, a specific protein phosphatase type 1 partner, in Plasmodium berghei in asexual erythrocytic proliferation and transmission. PLoS Pathog. 2019;15: e1007973.
Ponnudurai T, Lensen AH, van Gemert GJ, Bensink MP, Bolmer M, Meuwissen JH. Sporozoite load of mosquitoes infected with Plasmodium falciparum. Trans R Soc Trop Med Hyg. 1989;83:67–70.
Hillyer JF, Strand MR. Mosquito hemocyte-mediated immune responses. Curr Opin Insect Sci. 2014;3:14–21.
Murdock CC, Moller-Jacobs LL, Thomas MB. Complex environmental drivers of immunity and resistance in malaria mosquitoes. Proc Biol Sci. 2013;280:20132030.
Hopwood JA, Ahmed AM, Polwart A, Williams GT, Hurd H. Malaria-induced apoptosis in mosquito ovaries: a mechanism to control vector egg production. J Exp Biol. 2001;204:2773–80.
Ahmed AM, Hurd H. Immune stimulation and malaria infection impose reproductive costs in Anopheles gambiae via follicular apoptosis. Microbes Infect. 2006;8:308–15.
Pigeault R, Villa M. Long-term pathogenic response to Plasmodium relictum infection in Culex pipiens mosquito. PLoS ONE. 2018;13: e0192315.
Jiang X, Peery A, Hall AB, Sharma A, Chen XG, Waterhouse RM, et al. Genome analysis of a major urban malaria vector mosquito, Anopheles stephensi. Genome Biol. 2014;15:459.
Sinka ME, Pironon S, Massey NC, Longbottom J, Hemingway J, Moyes CL, et al. A new malaria vector in Africa: predicting the expansion range of Anopheles stephensi and identifying the urban populations at risk. Proc Natl Acad Sci USA. 2020;117:24900–8.
Moller-Jacobs LL, Murdock CC, Thomas MB. Capacity of mosquitoes to transmit malaria depends on larval environment. Parasit Vectors. 2014;7:593.
Bompard A, Da DF, Yerbanga SR, Morlais I, Awono-Ambene PH, Dabire RK, et al. High Plasmodium infection intensity in naturally infected malaria vectors in Africa. Int J Parasitol. 2020;50:985–96.
Graumans W, Jacobs E, Bousema T, Sinnis P. When is a Plasmodium-infected mosquito an infectious mosquito? Trends Parasitol. 2020;36:705–16.
Acknowledgements
The authors would like to thank Courtnie Vickery, Tyrone Williams, Anne Elliot, Adam McHugh, and Jared Cooper for help with mosquito husbandry, and the UGA animal resources staff for mouse husbandry.
Funding
This work was funded by the University of Georgia and the NIH (5R01AI110793-04). JCS was funded by NIH T32 AI1060546. The funding bodies did not have any say in the design of the study and collection, analysis, interpretation of data or in writing the manuscript.
Author information
Authors and Affiliations
Contributions
AKP: conception, design, acquisition, analysis, interpretation, drafting the manuscript. JCS: acquisition, design, analysis, interpretation, revisions to the manuscript. BFF: acquisition, design. LS: acquisition. DAH: acquisition. DEK: acquisition. CCM: acquisition, analysis, interpretation, substantive revisions to the manuscript. All authors approved the submitted version. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Additional file 1: Figure S1.
Generation and genotyping of the transgenic P. berghei ANKA reporter line GFP-Lucama1-eef1a (1052cl1). (a) Schematic representation of the generation of GFP-Lucama1-eef1a, (line 1052cl1) obtained after transfection by flow- sorting. DNA construct pL1308 is linearized at the SacII sites and integration occurs by double cross-over into the neutral p230p locus on chromosome (chr) 3. The construct contains two reporter expression cassettes, both containing the gfp-luciferase fusion gene under the control of either the schizont-specific ama1 promoter or the constitutive eef1a promoter. (b) Southern analysis of PFG-separated chromosomes confirms integration of the DNA construct pL1308 into the p230p locus on chr 3 of GFP-Lucama1-eef1a (1052cl1). The chromosomes are hybridized using a probe recognizing the 3′utr Pbdhfr/ts of the SM of the integrated construct which also hybridizes to the endogenous Pbdhfr/ts (PBANKA_0719300) on chr 7; control: the reference clone cl15cy1 of the P. berghei ANKA strain.
Additional file 2: Figure S2.
Increasing yields predicted by (a) mean oocyst densities (yellow line) correspond with increasing uncertainty (yellow shaded area). (b) In groups with higher mean oocyst densities (e.g., 45), estimating the contribution of time may be difficult because of the possibility of pooling individuals with heavily infected midgut (~ 50 oocysts, left pane) consisting of some oocysts that have contributed sporozoites already (arrows) and some still in the process of doing so (arrowheads), with another individual with low infected midgut (4 oocysts, right pane) where the entire contingent of sporozoites have been released (arrowheads). Images were taken at 400 × magnification at 26 days post-blood meal, from individuals whose salivary glands were combined into the same pool.
Additional file 3: Table S1
. Sampling regime for collecting sporozoites from 46 groups of mosquitoes, infected with two strains of P. berghei, over time (17–29 days post-blood meal); note salivary glands were not collected from any group at 18 days post-blood meal. Checkmarks indicate when sample collections were performed between 17 and 29 days post-blood meal from the respective groups; multiple check marks for the same group depict when sporozoites were collected for that group.
Additional file 4: Table S2.
Sample sizes and measures of parasite infection in the midguts.
Additional file 5: Table S3
. The full and minimal versions of the ‘offset’ model of sporozoite yields to adjust for differences in the number of salivary glands sampled (also see Table 1 for the ‘default’ model, and ‘Data analyses and statistical modelling’ section for rationale).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
About this article
Cite this article
Pathak, A.K., Shiau, J.C., Franke-Fayard, B. et al. Streamlining sporozoite isolation from mosquitoes by leveraging the dynamics of migration to the salivary glands. Malar J 21, 264 (2022). https://doi.org/10.1186/s12936-022-04270-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12936-022-04270-y