Mass of Y(3940) in Bethe–Salpeter equation for quarks

Abstract

The general form of the Bethe–Salpeter wave functions for the bound states composed of two vector fields of arbitrary spin and definite parity is corrected. Using the revised general formalism, we investigate the observed Y(3940) state, which is considered as a molecule state consisting of $D^{*0}\bar{D}^{*0}$. Though the attractive potential between $D^{*0}$ and $\bar{D}^{*0}$ including one light meson ($\sigma$, $\pi$, $\omega$, $\rho$) exchange is considered, we find that in our approach the contribution from one-$\pi$ exchange is equal to zero and consider SU(3) symmetry breaking. The obtained mass of Y(3940) is consistent with the experimental value.

1 Introduction

The exotic state Y(3940) was discovered by the Belle collaboration [1] and then confirmed by the BABAR collaboration [2]. The investigation of the structure of Y is of great significance, while the conventional $c\bar{c}$ charmonium interpretation for this state is disfavored [3]. Then possible alternative interpretations have been proposed, such as hadronic molecule and tetraquark states. Following the experimental results, it is suggested in Ref. [4] that the Y(3940) is a hadronic molecule state of $D^{*0}\bar{D}^{*0}$. However, in previous work [4], the numerical result of the binding energy for the molecule state sensitively depends on the value of typical cutoff in the effective interaction potential between two heavy vector mesons, and these two heavy mesons are considered as pointlike objects. Furthermore, the spin–parity quantum numbers $J^P$ of the Y(3940) are not unambiguously determined in experiment, except for $C=+$. The molecule state hypothesis implies that the quantum numbers of Y(3940) are $0^+$ or $2^+$, but Ref. [4] cannot deduce the definite quantum numbers in theory.

Though the general form of the Bethe–Salpeter (BS) wave functions for the bound states consisting of two vector fields of arbitrary spin and definite parity has been given in Ref. [5], we find that the derivation of this formalism has a serious defect. In this work, the general formalism is firstly corrected. Then we assume that the Y(3940) state is a molecule state composed of two heavy vector mesons $D^{*0}\bar{D}^{*0}$ and the revised general formalism is applied to the investigation of this two-body system. To construct the interaction kernel between two heavy mesons derived from one light meson ($\sigma$, $\pi$, $\omega$, $\rho$) exchange, we consider that the heavy meson is not a pointlike particle but a bound state composed of u-quark and c-quark and then investigate the light meson interaction with the u-quark in the heavy meson. Through the form factor we can obtain the light meson interaction with heavy meson and the potential between two heavy mesons without an extra parameter [6, 7]. Obviously, this potential in our approach contains more inspiration of quantum chromodynamics (QCD). Finally, numerically solving the relativistic Schrödinger-like equation with this potential, we can obtain the mass of the molecule state and then deduce the definite quantum numbers of the Y(3940) system.

In this work, one-$\pi$ exchange is considered in the interaction kernel between two heavy mesons. When investigating this pseudoscalar meson interaction with the u-quark in the heavy meson, we find that the coupling $\fancyscript{L}_I=ig_\pi \bar{u}\gamma _5u\pi$ should have no contribution to this interaction and represent it as the derivative coupling Lagrangian $\fancyscript{L}_I=if_\pi \bar{u}\gamma _\mu \gamma _5u\partial _\mu \pi$. In this approach we find that one-$\pi$ exchange has no contribution to the potential between two heavy vector mesons. Besides, it should be noted that the flavor-SU(3) singlet and octet states of vector mesons mix to form the physical $\omega$ and $\phi$ mesons, so the exchange mesons between two heavy mesons should not be the physical mesons but rather the singlet and octet states. Then in the interaction kernel between two heavy mesons SU(3) symmetry breaking should be considered.

This paper has the following structure. In Sect. 2 the revised general form of BS wave functions for the bound states composed of two vector fields with arbitrary spin and definite parity is given. In Sect. 3 we show the BS wave functions for the molecule states of $D^{*0}\bar{D}^{*0}$ with $J^P=0^+$ and $2^+$. After constructing the interaction kernel between two heavy vector mesons, we obtain the Schrödinger type equations in instantaneous approximation. In Sect. 4 we show how to calculate the form factors of the heavy meson $D^*$. Then the interaction potential and the mass of Y are calculated. Sections 5 and 6 give our numerical result and conclusion.

2 Revised general form of the BS wave functions

If a bound state of spin $j$ and parity $\eta _{P'}$ is composed of two vector fields with masses $M_1$ and $M_2$, respectively, its BS wave function is a $4\times 4$ matrix

$$\begin{aligned} \chi _{P'(\lambda \tau )}^j(x_1',x_2')=\langle 0|TA_\lambda (x_1')A_\tau (x_2')|P',j\rangle , \end{aligned}$$

(1)

which can be written as

$$\begin{aligned} \chi _{P'(\lambda \tau )}^j(x_1',x_2')=\mathrm{e}^{iP'\cdot X'}\chi _{P'(\lambda \tau )}^j(x'), \end{aligned}$$

(2)

where $X'=\eta _1x_1'+\eta _2x_2'$, $x'=x_1'-x_2'$ and $\eta _{1,2}$ are two positive quantities such that $\eta _{1,2}=M_{1,2}/(M_1+M_2)$. Then one has the BS wave function in the momentum representation

$$\begin{aligned} \chi _{\lambda \tau }^j(P',p')=\int \mathrm{d}^4x'e^{-ip'\cdot x'}\chi _{P'(\lambda \tau )}^j(x'), \end{aligned}$$

(3)

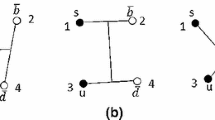
where $P'$ is the momentum of the bound state, $p'$ is the relative momentum of two vector fields and we have $P'=p_1'+p_2', p'=\eta _2p_1'-\eta _1p_2'$; $p_1'$ and $p_2'$ are the momenta of two vector fields, respectively. This is shown in Fig. 1.

Fig. 1

Bethe–Salpeter wave function for the bound state composed of two vector fields

The polarization tensor $\eta _{\mu _1\mu _2\cdots \mu _j}$ describing the spin of the bound state can be separated,

$$\begin{aligned} \chi _{\lambda \tau }^j(P',p')=\eta _{\mu _1\mu _2\cdots \mu _j}\chi _{\mu _1\mu _2\cdots \mu _j\lambda \tau }(P',p'), \end{aligned}$$

(4)

and the polarization tensor is totally symmetric, transverse, and traceless:

$$\begin{aligned} \eta _{\mu _1\mu _2\cdots }=\eta _{\mu _2\mu _1\cdots },\quad P'_{\mu _1}\eta _{\mu _1\mu _2\cdots }=0,\quad \eta _{\mu _1\mu _2\cdots }^{\mu _1}=0. \end{aligned}$$

(5)

Because of Eq. (5), $\chi _{\mu _1\cdots \mu _j\lambda \tau }$ is totally symmetric with respect to the indices $\mu _1,\ldots ,\mu _j$. It is necessary to note that the polarization tensor $\eta _{\mu _1\mu _2\cdots \mu _j}$ of the vector–vector bound state should contain all contributions from the spins of two vector fields and then $\chi _{\mu _1\cdots \mu _j\lambda \tau }$ should be independent of the polarization vectors of two vector fields. Therefore, from the BS wave function (1) and Lorentz covariance, we have

$$\begin{aligned}&\chi _{\mu _1\cdots \mu _j\lambda \tau }=p'_{\mu _1}\cdots p'_{\mu _j}[g_{\lambda \tau }f_1+(P'_\lambda p'_\tau +P'_\tau p'_\lambda )f_2\nonumber \\&\qquad +(P'_\lambda p'_\tau -P'_\tau p'_\lambda )f_3+P'_\lambda P'_\tau f_4+p'_\lambda p'_\tau f_5]\nonumber \\&\qquad +(p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\lambda } p'_\tau +p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\tau } p'_\lambda )f_6\nonumber \\&\qquad +(p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\lambda } p'_\tau -p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\tau } p'_\lambda )f_7\nonumber \\&\qquad +(p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\lambda } P'_\tau +p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\tau } P'_\lambda )f_8\nonumber \\&\qquad +(p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\lambda } P'_\tau -p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\tau } P'_\lambda )f_9\nonumber \\&\qquad +p'_{\mu _1}\cdots p'_{\mu _j}\epsilon _{\lambda \tau \xi \zeta }p'_\xi P'_\zeta f_{10}\nonumber \\&\qquad +p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }p'_\xi f_{11}\nonumber \\&\qquad +p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }P'_\xi f_{12}\nonumber \\&\qquad +(p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \xi \zeta }p'_\xi P'_\zeta p'_\tau \nonumber \\&\qquad +p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\tau \xi \zeta }p'_\xi P'_\zeta p'_\lambda )f_{13}\nonumber \\&\qquad +(p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \xi \zeta }p'_\xi P'_\zeta p'_\tau \nonumber \\&\qquad -p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\tau \xi \zeta }p'_\xi P'_\zeta p'_\lambda )f_{14}\nonumber \\&\qquad +(p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \xi \zeta }p'_\xi P'_\zeta P'_\tau \nonumber \\&\qquad +p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\tau \xi \zeta }p'_\xi P'_\zeta P'_\lambda )f_{15}\nonumber \\&\qquad +(p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \xi \zeta }p'_\xi P'_\zeta P'_\tau \nonumber \\&\qquad -p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\tau \xi \zeta }p'_\xi P'_\zeta P'_\lambda )f_{16}, \end{aligned}$$

(6)

where $\{\mu _1,\ldots ,\mu _j\}$ represents symmetrization of the indices $\mu _1,\ldots ,\mu _j$. There are only 16 scalar functions $f_i(P'\cdot p',p'^2)(i=1,\ldots ,16)$ in (6). In Ref. [5] the derivation of Eqs. (6, 7) has some errors, and they have been revised as (6) in this paper. From the massive vector field commutators for arbitrary times $x'_{10}$ and $x'_{20}$

$$\begin{aligned}{}[A_\lambda (x'_1),A_\tau (x'_2)]&=0\quad \text {for}\,M_1\ne M_2,\\ [A_\lambda (x'_1),A_\tau (x'_2)]&=i\left( \delta _{\lambda \tau }-\frac{\partial _\lambda \partial _\tau }{M_1^2}\right) \Delta '(x'_1-x'_2)\\&\qquad \text {for}\,M_1=M_2, \end{aligned}$$

where the right side of second equation is a c-number function; we may write

$$\begin{aligned} \langle 0|TA_\lambda (x_1')A_\tau (x_2')|P',j\rangle =\langle 0|TA_\tau (x_2')A_\lambda (x_1')|P',j\rangle . \end{aligned}$$

(7)

So we see that in the momentum representation the BS wave function of two equal or different vector fields is invariant under the substitutions $p'_1\rightarrow p'_2$ and $p'_2\rightarrow p'_1$, i.e.,

$$\begin{aligned} \chi _{\lambda \tau }^j(P',p')=\chi _{\tau \lambda }^j(P',-p'). \end{aligned}$$

(8)

This invariance is similar to crossing symmetry, which implies that the scalar functions in Eq. (6) have the following properties: for $j=2n,~n=0,1,2,3\ldots$,

$$\begin{aligned} f_i(P'\cdot p',p'^2)&=+f_i(-P'\cdot p',p'^2)\nonumber \\&\ \quad i =1,3,4,5,6,9,10,12,14,15,\end{aligned}$$

(9a)

$$\begin{aligned} f_i(P'\cdot p',p'^2)&=-f_i(-P'\cdot p',p'^2)\nonumber \\ {}&\ \quad i=2,7,8,11,13,16, \end{aligned}$$

(9b)

and, for $j=2n+1,\ n=0,1,2,3\ldots$,

$$\begin{aligned} f_i(P'\cdot p',p'^2)&=+f_i(-P'\cdot p',p'^2)\nonumber \\ {}&\ \quad i=2,7,8,11,13,16,\end{aligned}$$

(9c)

$$\begin{aligned} f_i(P'\cdot p',p'^2)&=-f_i(-P'\cdot p',p'^2)\nonumber \\ {}&\ \quad i=1,3,4,5,6,9,10,12,14,15. \end{aligned}$$

(9d)

Then we will reduce the general form without any assumption and approximation.

For the interacting massive vector field $A_\mu (x)$, the true equation of motion is

$$\begin{aligned} \partial _\nu \text {f}_{\nu \mu }-M_A^2A_\mu =-2gj_\mu , \end{aligned}$$

where the field strength tensor $\text {f}_{\nu \mu }$ is antisymmetric, $M_A$ is the vector field mass, and $g$ is the coupling constant. Because $j_\mu$ is a conserved current, one can obtain that $A_\mu$ with interactions should satisfy the subsidiary condition $\partial _\mu A_\mu (x)=0$ [8]. Using this subsidiary condition for the massive vector field and the equal-time commutation relation, we get

$$\begin{aligned} \partial _{1\lambda }TA_\lambda (x_1')A_\tau (x_2')=\partial _{2\tau }TA_\lambda (x_1')A_\tau (x_2')=0. \end{aligned}$$

The proof has been given by Ref. [5]. The BS wave function in Eq. (1) obeys this relation:

$$\begin{aligned}&\partial _{1\lambda }\langle 0|TA_\lambda (x_1')A_\tau (x_2')|P',j\rangle \\&\quad =\partial _{2\tau }\langle 0|TA_\lambda (x_1')A_\tau (x_2')|P',j\rangle =0, \end{aligned}$$

and in the momentum representation

$$\begin{aligned} p'_{1\lambda }\chi ^j_{\lambda \tau }(P',p')=p'_{2\tau }\chi ^j_{\lambda \tau }(P',p')=0. \end{aligned}$$

(10)

Substituting Eqs. (4) and (6) into (10), we obtain a set of independent equations, for $j=0$,

$$\begin{aligned} f_1\!+\!(\eta _1P'^2\!+\!P'\cdot p')(f_2\!+\!f_3)\!+\!(\eta _1P'\cdot p'\!+\!p'^2)f_5&=0,\nonumber \\ \eta _1f_1\!+\!(\eta _1P'\cdot p'\!+\!p'^2)(f_2-f_3)\!+\!(\eta _1P'^2\!+\!P'\cdot p')f_4&=0,\nonumber \\ \eta _2f_1\!+\!(\eta _2P'\cdot p'-p'^2)(f_2\!+\!f_3)\!+\!(\eta _2P'^2-P'\cdot p')f_4&\!=\!0, \end{aligned}$$

(11a)

and, for $j\ne 0$,

$$\begin{aligned}&f_1+(\eta _1P'^2+P'\cdot p')(f_2+f_3)\nonumber \\&\quad +(\eta _1P'\cdot p'+p'^2)f_5+j!f_6+j!f_7=0,\nonumber \\&\eta _1f_1+(\eta _1P'\cdot p'+p'^2)(f_2-f_3)\nonumber \\&\quad +(\eta _1P'^2+P'\cdot p')f_4+j!f_8+j!f_9=0,\nonumber \\&\eta _2f_1+(\eta _2P'\cdot p'-p'^2)(f_2+f_3)\nonumber \\&\quad +(\eta _2P'^2-P'\cdot p')f_4-j!f_8+j!f_9=0,\nonumber \\&(\eta _1P'\cdot p'+p'^2)(f_6-f_7)\nonumber \\&\quad +(\eta _1P'^2+P'\cdot p')(f_8-f_9)=0,\nonumber \\&(\eta _2P'\cdot p'-p'^2)(f_6+f_7)\nonumber \\&\quad +(\eta _2P'^2-P'\cdot p')(f_8+f_9)=0,\nonumber \\&\eta _1f_{11}-f_{12}+(\eta _1P'\cdot p'+p'^2)(f_{13}-f_{14})\nonumber \\&\quad +(\eta _1P'^2+P'\cdot p')(f_{15}-f_{16})=0,\nonumber \\&-\eta _2f_{11}-f_{12}+(\eta _2P'\cdot p'-p'^2)(f_{13}\nonumber \\&\quad +f_{14})+(\eta _2P'^2-P'\cdot p')(f_{15}+f_{16})=0. \end{aligned}$$

(11b)

For the sake of simplicity, we introduce $\phi _{1,2}$ and $\psi _{1}$ to replace $f_{4,5}$ and $f_{10}$, respectively, for $j=0$,

$$\begin{aligned} f_4&=-\eta _1\eta _2\phi _1+[\eta _1\eta _2(\eta _1\eta _2P'^2-\eta _1P'\cdot p'\\&\quad +\eta _2P'\cdot p'-p'^2)-\eta _1^2(\eta _2^2P'^2-2\eta _2P'\cdot p'+p'^2)\\&\quad -\eta _2^2(\eta _1^2P'^2+2\eta _1P'\cdot p'+p'^2)]\phi _2,\\ f_5&=\phi _1-[(\eta _1\eta _2P'^2-\eta _1P'\cdot p'+\eta _2P'\cdot p'-p'^2)\\&\quad +(\eta _1^2P'^2+2\eta _1P'\cdot p'+p'^2)\\&\quad +(\eta _2^2P'^2-2\eta _2P'\cdot p'+p'^2)]\phi _2,\\ f_{10}&=\psi _1, \end{aligned}$$

and introduce $\phi _{1,2,3,4}$ and $\psi _{1,2,3,4,5}$ to replace $f_{4,5,6,7}$ and $f_{10,13,14,15,16}$, respectively, for $j\ne 0$,

$$\begin{aligned} f_4&=-\eta _1\eta _2\phi _1\!+\![\eta _1\eta _2(\eta _1\eta _2P'^2-\eta _1P'\cdot p'\\&\quad +\eta _2P'\cdot p'-p'^2)-\eta _1^2(\eta _2^2P'^2-2\eta _2P'\cdot p'\!+\!p'^2)\\&\quad -\eta _2^2(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)]\phi _2\!+\!\eta _1(\eta _2P'\cdot p'\\&\quad -p'^2)\phi _3-\eta _2(\eta _1P'\cdot p'\!+\!p'^2)\phi _4,\\ f_5&=\phi _1-[(\eta _1\eta _2P'^2-\eta _1P'\cdot p'\!+\!\eta _2P'\cdot p'-p'^2)\\&\quad +(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)\!+\!(\eta _2^2P'^2-2\eta _2P'\cdot p'\\&\quad +p'^2)]\phi _2-(\eta _2P'^2-P'\cdot p')\phi _3-(\eta _1P'^2\!+\!P'\cdot p')\phi _4,\\ f_6&=[(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)(\eta _2P'^2-P'\cdot p')\phi _3\\&\quad +(\eta _2^2P'^2-2\eta _2P'\cdot p'\!+\!p'^2)(\eta _1P'^2\!+\!P'\cdot p')\phi _4]/(2j!),\\ f_7&=[(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)(\eta _2P'^2-P'\cdot p')\phi _3\\&\quad -(\eta _2^2P'^2-2\eta _2P'\cdot p'\!+\!p'^2)(\eta _1P'^2\!+\!P'\cdot p')\phi _4]/(2j!),\\ f_{10}&=\psi _1,\quad f_{13}=\psi _2,\quad f_{14}=\psi _3,\quad f_{15}=\psi _4,\quad f_{16}=\psi _5, \end{aligned}$$

where $\phi _i(P'\cdot p',p'^2)$ and $\psi _i(P'\cdot p',p'^2)$ are independent scalar functions. Solving the set of equations (11), we see that $f_{1,2,3,8,9,11,12}$ are the functions of $\phi _i$ and $\psi _i$: for $j=0$,

$$\begin{aligned} f_1&=(\eta _1\eta _2P'^2-\eta _1P'\cdot p'+\eta _2P'\cdot p'-p'^2)\phi _1\\&\quad +(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)(\eta _2^2P'^2\!-\!2\eta _2P'\cdot p'\!+\!p'^2)\phi _2,\\ f_2&=(\eta _1-\eta _2)\phi _1/2+[(\eta _2-\eta _1)(\eta _1\eta _2P'^2-\eta _1P'\cdot p'\\&\quad +\eta _2P'\cdot p'-p'^2)/2-\eta _1(\eta _2^2P'^2-2\eta _2P'\cdot p'+p'^2)\\&\quad +\eta _2(\eta _1^2P'^2+2\eta _1P'\cdot p'+p'^2)]\phi _2,\\ f_3&=-\phi _1/2\!-\!(\eta _1\eta _2P'^2\!-\!\eta _1P'\cdot p'\!+\!\eta _2P'\cdot p'\!-\!p'^2)\phi _2/2, \end{aligned}$$

and, for $j\ne 0$,

$$\begin{aligned} f_1&=(\eta _1\eta _2P'^2-\eta _1P'\cdot p'\!+\!\eta _2P'\cdot p'-p'^2)\phi _1\\&\quad +(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)(\eta _2^2P'^2\!-\!2\eta _2P'\cdot p'\!+\!p'^2)\phi _2,\\ f_2&=(\eta _1-\eta _2)\phi _1/2\!+\![(\eta _2-\eta _1)(\eta _1\eta _2P'^2-\eta _1P'\cdot p'\\&\quad +\eta _2P'\cdot p'-p'^2)/2-\eta _1(\eta _2^2P'^2-2\eta _2P'\cdot p'\!+\!p'^2)\\&\quad +\eta _2(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)]\phi _2\\&\quad +[(\eta _2-\eta _1)(\eta _1\eta _2P'^2-\eta _1P'\cdot p'\!+\!\eta _2P'\cdot p'-p'^2)/2\\&\quad -\eta _1(\eta _2^2P'^2-2\eta _2P'\cdot p'\!+\!p'^2)]\phi _3\\&\quad +[(\eta _2-\eta _1)(\eta _1\eta _2P'^2-\eta _1P'\cdot p'\!+\!\eta _2P'\cdot p'-p'^2)/2\\&\quad +\eta _2(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)]\phi _4,\\ f_3&=-\phi _1/2-(\eta _1\eta _2P'^2-\eta _1P'\cdot p'\!+\!\eta _2P'\cdot p'\\&\quad -p'^2)(\phi _2\!+\!\phi _3\!+\!\phi _4)/2,\\ f_8&=[-(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)(\eta _2P'\cdot p'-p'^2)\phi _3\\&\quad -(\eta _2^2P'^2-2\eta _2P'\cdot p'\!+\!p'^2)(\eta _1P'\cdot p'\!+\!p'^2)\phi _4]/(2j!),\\ f_9&=[-(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)(\eta _2P'\cdot p'-p'^2)\phi _3\\&\quad +(\eta _2^2P'^2-2\eta _2P'\cdot p'\!+\!p'^2)(\eta _1P'\cdot p'\!+\!p'^2)\phi _4]/(2j!),\\ f_{11}&=(\eta _2P'\cdot p'-\eta _1P'\cdot p'-2p'^2)\psi _2\!+\!(P'\cdot p')\psi _3\\&\quad +(\eta _2P'^2-\eta _1P'^2-2P'\cdot p')\psi _4\!+\!P'^2\psi _5,\\ f_{12}&=(2\eta _1\eta _2P'\cdot p'\!+\!\eta _2p'^2-\eta _1p'^2)\psi _2-p'^2\psi _3\\&\quad +(2\eta _1\eta _2P'^2\!+\!\eta _2P'\cdot p'-\eta _1P'\cdot p')\psi _4-(P'\cdot p')\psi _5. \end{aligned}$$

Then the BS wave function of the bound state becomes

$$\begin{aligned} \chi _{\lambda \tau }^{j=0}(P',p')&=T^1_{\lambda \tau }\phi _1+T^2_{\lambda \tau }\phi _2+\epsilon _{\lambda \tau \xi \zeta }p'_\xi P'_\zeta \psi _1,\end{aligned}$$

(12)

$$\begin{aligned} \chi _{\lambda \tau }^{j\ne 0}(P',p')&=\eta _{\mu _1\cdots \mu _j}[p'_{\mu _1}\cdots p'_{\mu _j}(T^1_{\lambda \tau }\phi _1+T^2_{\lambda \tau }\phi _2)\nonumber \\&\quad +T^3_{\lambda \tau }\phi _3+T^4_{\lambda \tau }\phi _4 +p'_{\mu _1}\cdots p'_{\mu _j}\epsilon _{\lambda \tau \xi \zeta }p'_\xi P'_\zeta \psi _1\nonumber \\&\quad +T^5_{\lambda \tau }\psi _2+T^6_{\lambda \tau }\psi _3+T^7_{\lambda \tau }\psi _4+T^8_{\lambda \tau }\psi _5], \end{aligned}$$

(13)

where

$$\begin{aligned} T_{\lambda \tau }^1&=(\eta _1\eta _2P'^2-\eta _1P'\cdot p'+\eta _2P'\cdot p'-p'^2)g_{\lambda \tau }\\&\quad -(\eta _1\eta _2P'_{\lambda }P'_{\tau }+\eta _2P'_{\lambda }p'_{\tau }-\eta _1p'_{\lambda }P'_{\tau }-p'_{\lambda }p'_{\tau }), \end{aligned}$$

$$\begin{aligned} T_{\lambda \tau }^2&=(\eta _1^2P'^2\!+\!2\eta _1P'\cdot p'\!+\!p'^2)(\eta _2^2P'^2\!-\! 2\eta _2P'\cdot p'\!+\!p'^2)g_{\lambda \tau }\\&\quad +(\eta _1\eta _2P'^2-\eta _1P'\cdot p'+\eta _2P'\cdot p'-p'^2)\\&\quad \times (\eta _1\eta _2P'_{\lambda }P'_{\tau }-\eta _1P'_{\lambda }p'_{\tau }+\eta _2p'_{\lambda }P'_{\tau }-p'_{\lambda }p'_{\tau })\\&\quad -(\eta _2^2P'^2-2\eta _2P'\cdot p'+p'^2)(\eta _1 ^2P'_{\lambda }P'_{\tau }+\eta _1P'_{\lambda }p'_{\tau }\\&\quad +\eta _1p'_{\lambda }P'_{\tau }+p'_{\lambda }p'_{\tau })\\&\quad -(\eta _1^2P'^2+2\eta _1P'\cdot p'+p'^2)(\eta _2 ^2P'_{\lambda }P'_{\tau }\\&\quad -\eta _2P'_{\lambda }p'_{\tau }-\eta _2p'_{\lambda }P'_{\tau }+p'_{\lambda }p'_{\tau }), \end{aligned}$$

$$\begin{aligned} T_{\lambda \tau }^3&=\frac{1}{j!}p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\lambda }(\eta _1^2P'^2+2\eta _1P'\cdot p'+p'^2)\\&\quad \times [(\eta _2^2P'^2-2\eta _2P'\cdot p'+p'^2)(\eta _1P'+p')_{\tau }\\&\quad -(\eta _1\eta _2P'^2\!-\!\eta _1P'\cdot p'\!+\!\eta _2P'\cdot p'\!-\!p'^2)(\eta _2P'\!-\!p')_{\tau }]\\&\quad -p'_{\mu _1}\cdots p'_{\mu _j}[(\eta _2^2P'^2-2\eta _2P'\cdot p'+p'^2)\\&\quad \times (\eta _1 ^2P'_{\lambda }P'_{\tau }+\eta _1P'_{\lambda }p'_{\tau }+\eta _1p'_{\lambda }P'_{\tau }+p'_{\lambda }p'_{\tau })\\&\quad -(\eta _1\eta _2P'^2-\eta _1P'\cdot p'+\eta _2P'\cdot p'-p'^2)\\&\quad \times (\eta _1\eta _2P'_{\lambda }P'_{\tau }-\eta _1P'_{\lambda }p'_{\tau }+\eta _2p'_{\lambda }P'_{\tau }-p'_{\lambda }p'_{\tau })], \end{aligned}$$

$$\begin{aligned} T_{\lambda \tau }^4&=\frac{1}{j!}p'_{\{\mu _2}\cdots p'_{\mu _j}g_{\mu _1\}\tau }(\eta _2^2P'^2-2\eta _2P'\cdot p'+p'^2)\\&\quad \times [(\eta _1\eta _2P'^2-\eta _1P'\cdot p'+\eta _2P'\cdot p'-p'^2)\\&\quad \times (\eta _1P'+p')_{\lambda }\\&\quad -(\eta _1^2P'^2+2\eta _1P'\cdot p'+p'^2)(\eta _2P'-p')_{\lambda }]\\&\quad -p'_{\mu _1}\cdots p'_{\mu _j}[(\eta _1^2P'^2+2\eta _1P'\cdot p'+p'^2)\\&\quad \times (\eta _2 ^2P'_{\lambda }P'_{\tau }-\eta _2P'_{\lambda }p'_{\tau }-\eta _2p'_{\lambda }P'_{\tau }+p'_{\lambda }p'_{\tau })\\&\quad -(\eta _1\eta _2P'^2-\eta _1P'\cdot p'+\eta _2P'\cdot p'-p'^2)\\&\quad \times (\eta _1\eta _2P'_{\lambda }P'_{\tau }-\eta _1P'_{\lambda }p'_{\tau }+\eta _2p'_{\lambda }P'_{\tau }-p'_{\lambda }p'_{\tau })], \end{aligned}$$

$$\begin{aligned} T_{\lambda \tau }^5&=(\eta _2P'\cdot p'-\eta _1P'\cdot p'-2p'^2)p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }p'_\xi \\&\quad +(2\eta _1\eta _2P'\cdot p'\!+\!\eta _2p'^2\!-\!\eta _1p'^2)p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }P'_\xi \\&\quad +p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \xi \zeta }p'_\xi P'_\zeta p'_\tau +p'_{\{\mu _2}\\&\quad \cdots p'_{\mu _j}\epsilon _{\mu _1\}\tau \xi \zeta }p'_\xi P'_\zeta p'_\lambda , \end{aligned}$$

$$\begin{aligned} T_{\lambda \tau }^6&=(P'\cdot p')p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }p'_\xi \\&\quad -p'^2p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }P'_\xi \\&\quad +p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \xi \zeta }p'_\xi P'_\zeta p'_\tau \\&\quad -p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\tau \xi \zeta }p'_\xi P'_\zeta p'_\lambda , \end{aligned}$$

$$\begin{aligned} T_{\lambda \tau }^7&=(\eta _2P'^2-\eta _1P'^2-2P'\cdot p')p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }p'_\xi \\&\quad +(2\eta _1\eta _2P'^2+\eta _2P'\cdot p'-\eta _1P'\cdot p')p'_{\{\mu _2}\\&\quad \cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }P'_\xi +p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \xi \zeta }p'_\xi P'_\zeta P'_\tau \\&\quad +p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\tau \xi \zeta }p'_\xi P'_\zeta P'_\lambda , \end{aligned}$$

$$\begin{aligned} T_{\lambda \tau }^8&=P'^2p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }p'_\xi \\&\quad -(P'\cdot p')p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \tau \xi }P'_\xi \\&\quad +p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\lambda \xi \zeta }p'_\xi P'_\zeta P'_\tau \\&\quad -p'_{\{\mu _2}\cdots p'_{\mu _j}\epsilon _{\mu _1\}\tau \xi \zeta }p'_\xi P'_\zeta P'_\lambda . \end{aligned}$$

This derivation makes use of the fact that $P'$, $p'$, and $\eta _{\mu _1\cdots \mu _j}$ are linearly independent. In Ref. [5] Eqs. (18–19) are wrong, they are revised as (12) and (13) in this paper.

Now, under space reflection

$$\begin{aligned} x_i'\rightarrow x_i''=-x_i',\quad x_0''=x_0', \end{aligned}$$

one has

$$\begin{aligned}&\mathsf P A_\lambda (x')\mathsf P ^{-1}=\fancyscript{P}_{\lambda \xi } A_\xi (x''),\nonumber \\&\quad \fancyscript{P}_{\lambda \xi }=\left( \begin{array}{llll} -1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad -1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad -1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{array} \right) ,\\&\mathsf P |0\rangle =|0\rangle ,\quad \mathsf P |P',j\rangle =\eta _{P'}|P'',j\rangle ,\nonumber \end{aligned}$$

(14)

with $x''=(-\mathbf x ',x_0')$ and $P''=(-\mathbf{P}',P_0')$.

We obtain the properties of the BS wave function under space reflection from Eqs. (1) and (14):

$$\begin{aligned} \chi _{P'(\lambda \tau )}^{j}(x_1',x_2')=\eta _{P'}\fancyscript{P}_{\lambda \xi }\fancyscript{P}_{\tau \zeta }\chi _{P''(\xi \zeta )}^{j}(x_1'',x_2'') \end{aligned}$$

(15)

and in the momentum representation

$$\begin{aligned} \chi _{\lambda \tau }^{j}(P',p')=\eta _{P'}\fancyscript{P}_{\lambda \xi }\fancyscript{P}_{\tau \zeta }\chi _{\xi \zeta }^{j}(P'',p''). \end{aligned}$$

(16)

From (4), (6), (12), (13), and (16), it is easy to derive, for $\eta _{P'}=(-1)^j$,

$$\begin{aligned} \chi _{\lambda \tau }^{j=0}(P',p')&=T^1_{\lambda \tau }\phi _1+T^2_{\lambda \tau }\phi _2,\end{aligned}$$

(17)

$$\begin{aligned} \chi _{\lambda \tau }^{j\ne 0}(P',p')&=\eta _{\mu _1\cdots \mu _j}[p'_{\mu _1}\cdots p'_{\mu _j}(T^1_{\lambda \tau }\phi _1+T^2_{\lambda \tau }\phi _2)\nonumber \\&\quad +T^3_{\lambda \tau }\phi _3+T^4_{\lambda \tau }\phi _4], \end{aligned}$$

(18)

and, for $\eta _{P'}=(-1)^{j+1}$,

$$\begin{aligned} \chi _{\lambda \tau }^{j=0}(P',p')&=\epsilon _{\lambda \tau \xi \zeta }p'_\xi P'_\zeta \psi _1,\end{aligned}$$

(19)

$$\begin{aligned} \chi _{\lambda \tau }^{j\ne 0}(P',p')&=\eta _{\mu _1\cdots \mu _j}(p'_{\mu _1}\cdots p'_{\mu _j}\epsilon _{\lambda \tau \xi \zeta }p'_\xi P'_\zeta \psi _1\nonumber \\&\quad +T^5_{\lambda \tau }\psi _2+T^6_{\lambda \tau }\psi _3+T^7_{\lambda \tau }\psi _4+T^8_{\lambda \tau }\psi _5). \end{aligned}$$

(20)

The general form of the BS wave functions for the bound states composed of two massive vector fields of arbitrary spin and definite parity is obtained. No matter how high the spin of the bound state is, its BS wave function should satisfy Eqs. (17), (18), (19) or (20). From (17) and (18), we conclude that the BS wave function of a bound state composed of two massive vector fields with spin $j\ne 0$ and parity $(-1)^j$ has only four independent components and that of a bound state with $J^P=0^+$ has only two independent components. From (19) and (20), we conclude that the BS wave function of a bound state with spin $j$ and parity $(-1)^{j+1}$ has only five independent components except for $j=0$ and one for $j=0$. Up to now, all the above analyses are model independent. In the next section we will apply the general formalism to investigate molecule states composed of two vector mesons.

3 The extended Bethe–Salpeter equation

Assuming that the Y(3940) is a S-wave molecule state consisting of two heavy vector mesons $D^{*0}$ and $\bar{D}^{*0}$, one can have $J^P=0^+$ or $2^+$ for this system. [4] From Eqs. (17) and (18), we can obtain the BS wave function describing this bound state, for $J^P=0^+$,

$$\begin{aligned} \chi _{\lambda \tau }^{{0^{+}}}(P',p')=T_{\lambda \tau }^{1}\mathcal {F}_1+T_{\lambda \tau }^{2}\mathcal {F}_2, \end{aligned}$$

(21)

or, for $J^P=2^+$,

$$\begin{aligned}&\chi _{\lambda \tau }^{2^{+}}(P',p')=\eta _{\mu _1\mu _2}[p'_{\mu _1} p'_{\mu _2}(T_{\lambda \tau }^{1}\mathcal {G}_1+T_{\lambda \tau }^2\mathcal {G}_2)\nonumber \\&\quad +T_{\lambda \tau }^3\mathcal {G}_3+T_{\lambda \tau }^4\mathcal {G}_4]. \end{aligned}$$

(22)

The BS wave function of this bound state satisfies the equation

$$\begin{aligned}&\chi _{\lambda \tau }(P',p')\nonumber \\&\quad =\int \frac{i\mathrm{d}^4q'}{(2\pi )^4}\Delta _{F\lambda \alpha }(p_1')\mathcal {V}_{\alpha \theta ,\beta \kappa }(p',q';P') \chi _{\theta \kappa }(P',q')\Delta _{F\beta \tau }(p_2'),\nonumber \\ \end{aligned}$$

(23)

where $\mathcal {V}_{\alpha \theta ,\beta \kappa }$ is the interaction kernel, we have the propagators for the spin 1 fields $\Delta _{F\lambda \alpha }(p_1')\!=\!(\delta _{\lambda \alpha }+\frac{p'_{1\lambda } p'_{1\alpha }}{M_1^2})\frac{1}{p_1'^2+M_1^2-i\epsilon }$, $\Delta _{F\beta \tau }(p_2')=(\delta _{\beta \tau }+\frac{p'_{2\beta } p'_{2\tau }}{M_2^2})\frac{1}{p_2'^2+M_2^2-i\epsilon }$, and the bound state momentum is set as $P'=(0,0,0,iM)$ in the rest frame. In Ref. [5], we have considered that the effective interaction between two heavy mesons is derived from one light meson ($\sigma$, $\omega$, $\rho$) exchange and obtained the result that the molecule state $D^{*0}\bar{D}^{*0}$ lies above the threshold. In this work, one-$\pi$ exchange is also considered and one-$\omega$ exchange is reconsidered, shown as in Fig. 2.

Fig. 2

The light meson exchange between two heavy mesons

Now, we construct the kernel between two heavy vector mesons from one-$\pi$ exchange. The charmed meson $D^{*}$ is composed of a heavy quark $c$ and a light antiquark $\bar{u}$. Owing to the large mass of the $c$-quark, the Lagrangian representing the interaction of $\pi$-meson triplet with quarks should be

$$\begin{aligned} \fancyscript{L}_I\!=\!ig_\pi \left( \begin{array}{ccc} \bar{u}&\quad \bar{d}&\quad \bar{c} \end{array} \right) \gamma _5 \left( \begin{array}{ccc} \pi ^0&{}\quad \sqrt{2}\pi ^+&{}\quad 0\\ \sqrt{2}\pi ^-&{}\quad -\pi ^0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0 \end{array}\right) \left( \begin{array}{l} u\\ d\\ c \end{array} \right) ,\nonumber \\ \end{aligned}$$

(24)

or

$$\begin{aligned} \fancyscript{L}_I&= if_\pi \left( \begin{array}{ccc} \bar{u}&\quad \bar{d}&\quad \bar{c} \end{array}\right) \gamma _\mu \gamma _5\nonumber \\&\times \left( \begin{array}{ccc} \partial _\mu \pi ^0&{}\quad \sqrt{2}\partial _\mu \pi ^+&{}\quad 0\\ \sqrt{2}\partial _\mu \pi ^-&{}\quad -\partial _\mu \pi ^0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0 \end{array} \right) \left( \begin{array}{c} u\\ d\\ c \end{array} \right) , \end{aligned}$$

(25)

where $g_\pi$ and $f_\pi$ are the $\pi$-meson–quark coupling constants, $g_\pi =\frac{340}{97}$ [9]. Because the contribution of Fig. 2 is from the term $i\bar{u}\gamma _5\pi ^0u$ or $i\bar{u}\gamma _\mu \gamma _5\partial _\mu \pi ^0u$, we set $f_\pi =\frac{g_\pi }{2m_u}$ and $m_u$ is u-quark mass. Then the effective quark current is $J^-=i\bar{u}\gamma _5 u$ or $J^+_\mu =i\bar{u}\gamma _\mu \gamma _5 u$ and the S-matrix element between two heavy mesons is

$$\begin{aligned} V_\pi =g_\pi ^2\langle V(p_1')|J^-|V(q_1')\rangle \frac{1}{k^2+m_\pi ^2}\langle V(p_2')|J^-|V(q_2')\rangle ,\nonumber \\ \end{aligned}$$

(26)

or

$$\begin{aligned} V_\pi&= f_\pi ^2\langle V(p_1')|J^+_\mu |V(q_1')\rangle k_\mu \frac{1}{k^2+m_\pi ^2}\nonumber \\&\times \,k_\nu \langle V(p_2')|J^+_\nu |V(q_2')\rangle , \end{aligned}$$

(27)

where $\langle V|J^-|V\rangle$ and $\langle V|J^+_\mu |V\rangle$ represent the vertices of the pseudoscalar meson interaction with the heavy vector meson, respectively. The matrix elements of these quark currents can be expressed as

$$\begin{aligned}&\langle V(p_1')|J^-|V(q_1') \rangle =\frac{1}{\sqrt{2E_1(p_1')}\sqrt{2E_1(q_1')}}\nonumber \\&\quad \times h^{-}(k^2)\epsilon _{abcd}p_{1a}'q_{1b}'\varepsilon ^*_c(p_1') \varepsilon _d(q_1'), \end{aligned}$$

(28)

$$\begin{aligned}&\langle V(p_2')|J^-|V(q_2') \rangle =\frac{1}{2\sqrt{E_2(p_2')E_2(q_2')}}\nonumber \\&\quad \times \bar{h}^{-}(k^2)\epsilon _{a'b'c'd'}p_{2a'}'q_{2b'}'\varepsilon ^*_{c'}(p_2') \varepsilon _{d'}(q_2'), \end{aligned}$$

(29)

$$\begin{aligned}&\langle V(p_1')|J^+_{\mu }|V(q_1') \rangle \nonumber \\&\quad =\frac{1}{2\sqrt{E_1(p_1')E_1(q_1')}}h^{(p)}(k^2)\epsilon _{\mu abc}\varepsilon ^*_a(p_1') \varepsilon _b(q_1')(p_{1}'+q_{1}')_c, \end{aligned}$$

(30)

$$\begin{aligned}&\langle V(p_2')|J^+_{\nu }|V(q_2') \rangle \nonumber \\&\quad =\frac{1}{2\sqrt{E_2(p_2')E_2(q_2')}}\bar{h}^{(p)}(k^2)\epsilon _{\nu a'b'c'}\varepsilon ^*_{a'}(p_2') \varepsilon _{b'}(q_2')(p_{2}' \!+\!q_{2}')_{c'}, \end{aligned}$$

(31)

where $p'_1=(\mathbf{p}',ip_{10}')$, $p'_2=(-\mathbf{p}',ip_{20}')$, $q'_1=(\mathbf{q}',iq_{10}')$, $q'_2=(-\mathbf{q}',iq_{20}')$, $k=p_1'-q_1'=q_2'-p_2'$ is the momentum of the light meson and $\mathbf{k}=\mathbf p '-\mathbf{q}'$; $h(k^2)$ and $\bar{h}(k^2)$ are scalar functions, the four-vector $\varepsilon (p)=(\varvec{\varepsilon }+\frac{(\varvec{\varepsilon }\cdot \mathbf{p})\mathbf p }{M_H(E_H(p)+M_H)},i\frac{\varvec{\varepsilon }\cdot \mathbf{p}}{M_H})$ is the polarization vector of heavy vector meson with momentum $\text {p}$, $E_H(p)=\sqrt{\mathbf{p}^2+M_H^2}$, $(\varvec{\varepsilon },0)$ is the polarization vector in the heavy meson rest frame. In our approach, considering that the exchange meson is off the mass shell, we calculate the meson–meson interaction when $k^2\ne -m^2$ and the heavy meson form factors $h(k^2)$ and $\bar{h}(k^2)$ are necessarily required. In Sect. 4, we will show that for the form factors $h^{-}(k^2)=\bar{h}^{-}(k^2)=0$. Then the effective interaction from one-$\pi$ exchange should have the form given by Eq. (27). Cutting the external lines containing the normalizations and polarization vectors $\varepsilon ^*_\alpha (p_1'), \varepsilon _\theta (q_1'), \varepsilon ^*_\beta (p_2'), \varepsilon _{\kappa }(q_2')$, we obtain the interaction kernel from one-$\pi$ exchange

$$\begin{aligned} \mathcal {V}^\pi _{\alpha \theta ,\beta \kappa }(p',q';P')&= f_\pi ^2h_1^{(p)}(k^2)\epsilon _{\mu \alpha \theta c}(p_1'+q_1')_ck_\mu \nonumber \\&\times \frac{1}{k^2+m_\pi ^2}\bar{h}_1^{(p)}(k^2)\epsilon _{\nu \beta \kappa c'}\nonumber \\&\times (p_2'+q_2')_{c'}k_\nu . \end{aligned}$$

(32)

Then we reconsider one-$\omega$ exchange between two heavy vector mesons. In hadronic physics, the physical $\omega$ and $\phi$ mesons are linear combinations of the SU(3) octet $V_8=(u\bar{u}+d\bar{d}-2s\bar{s})/\sqrt{6}$ and singlet $V_1=(u\bar{u}+d\bar{d}+s\bar{s})/\sqrt{3}$ as

$$\begin{aligned} \phi =-V_8\mathrm{cos}\theta +V_1\mathrm{sin}\theta ,\quad \omega =V_8\mathrm{sin}\theta +V_1\mathrm{cos}\theta , \end{aligned}$$

(33)

where the mixing angle $\theta =38.58^\circ$ was obtained by KLOE [10]. Because of the SU(3) symmetry, we consider that the exchange mesons are not the physical mesons and the exchanged mesons should be the octet $V_8$ and singlet $V_1$ states. From Eq. (33), we can obtain the relations of the octet–quark coupling constant $g_8$ and the singlet–quark coupling constant $g_1$

$$\begin{aligned} g_\phi =-g_8\mathrm{cos}\theta +g_1\mathrm{sin}\theta ,\quad g_\omega =g_8\mathrm{sin}\theta +g_1\mathrm{cos}\theta , \end{aligned}$$

(34)

where $g_\omega$ and $g_\phi$ are the corresponding meson–quark coupling constants, $g_\omega ^2=2.42$ and $g_\phi ^2=13.0$ [11]. Since the SU(3) is broken, the masses of the singlet $V_1$ and octet $V_8$ states are approximatively identified with the two physical masses of $\omega$ and $\phi$ mesons, respectively. The interaction kernel derived from one scalar meson exchange and one vector meson exchange has been given in Ref. [5], and the kernel from one light meson ($\pi$, $\sigma$, $\rho$, $V_1$, and $V_8$) exchange becomes

$$\begin{aligned}&\mathcal {V}_{\alpha \theta ,\beta \kappa }(p',q';P')\nonumber \\&\quad = h_1^{(p)}(k^2)\epsilon _{\mu \alpha \theta c}(p_1'+q_1')_ck_\mu \nonumber \\&\qquad \times \frac{f_\pi ^2}{k^2+m_\pi ^2}\bar{h}_1^{(p)}(k^2)\epsilon _{\nu \beta \kappa c'}(p_2'+q_2')_{c'}k_\nu \nonumber \\&\qquad +h_1^{(s)}(k^2)\frac{g_\sigma ^2}{k^2+m_\sigma ^2}\bar{h}_1^{(s)}(k^2)\delta _{\alpha \theta }\delta _{\beta \kappa }\nonumber \\&\qquad +\left( \frac{g_\rho ^2}{k^2+m_\rho ^2}+\frac{g_1^2}{k^2+m_\omega ^2}+\frac{g_8^2}{k^2+m_\phi ^2}\right) \nonumber \\&\qquad \times \{h_1^{(\text {v})}(k^2)\bar{h}_1^{(\text {v})}(k^2)(p_1'+q_1')\cdot (p_2'+q_2')\delta _{\alpha \theta }\delta _{\beta \kappa }\nonumber \\&\qquad -h_1^{(\text {v})}(k^2)\bar{h}_2^{(\text {v})}(k^2)\delta _{\alpha \theta }[q_{2\beta }'(p_1'+q_1')_\kappa \nonumber \\&\qquad +(p_1'+q_1')_\beta p_{2\kappa }']-h_2^{(\text {v})}(k^2)\bar{h}_1^{(\text {v})}(k^2)[q_{1\alpha }'(p_2'+q_2')_\theta \nonumber \\&\qquad +(p_2'+q_2')_\alpha p_{1\theta }']\delta _{\beta \kappa }+h_2^{(\text {v})}(k^2)\bar{h}_2^{(\text {v})}(k^2)[q_{1\alpha }'q_{2\beta }'\delta _{\theta \kappa }\nonumber \\&\qquad +q_{1\alpha }'\delta _{\theta \beta }p_{2\kappa }'+\delta _{\alpha \kappa }p_{1\theta }'q_{2\beta }'+\delta _{\alpha \beta }p_{1\theta }'p_{2\kappa }']\}, \end{aligned}$$

(35)

where $k=(\mathbf{k},0)$.

Firstly, we assume that the Y(3940) is a molecule state with $J^P=0^+$. Substituting its BS wave function given by Eq. (21) and the kernel (35) into the BS equation (23), we find that the integral of one term on the right-hand side of (21) has a contribution to the one of itself and the other term. Moreover, the cross terms contain the factors of $1/M_1^2$ and $1/M_2^2$, which are small for the masses of the heavy mesons are large. It is difficult to strictly solve the BS equation, and in this paper we use a simple approach to solve it as follows. Ignoring the cross terms, one can obtain two individual equations:

$$\begin{aligned} \mathcal {F}^1_{\lambda \tau }(P'\cdot p',p'^2)&= \int \frac{i\mathrm{d}^4q'}{(2\pi )^4}\Delta _{F\lambda \alpha }(p_1')\mathcal {V}_{\alpha \theta ,\beta \kappa }(p',q';P')\nonumber \\&\times \,\mathcal {F}^1_{\theta \kappa }(P'\cdot q',q'^2)\Delta _{F\beta \tau }(p_2'),\end{aligned}$$

(36)

$$\begin{aligned} \mathcal {F}^2_{\lambda \tau }(P'\cdot p',p'^2)&= \int \frac{i\mathrm{d}^4q'}{(2\pi )^4}\Delta _{F\lambda \alpha }(p_1')\mathcal {V}_{\alpha \theta ,\beta \kappa }(p',q';P')\nonumber \\&\times \,\mathcal {F}^2_{\theta \kappa }(P'\cdot q',q'^2)\Delta _{F\beta \tau }(p_2'), \end{aligned}$$

(37)

where $\mathcal {F}^1_{\lambda \tau }(P'\cdot p',p'^2)=T^1_{\lambda \tau }\mathcal {F}_1(P'\cdot p',p'^2)$ and $\mathcal {F}^2_{\lambda \tau }(P'\cdot p',p'^2)=T^2_{\lambda \tau }\mathcal {F}_2(P'\cdot p',p'^2)$. Solving these two equations, respectively, one can obtain two series of eigenvalues and eigenfunctions. Because the cross terms are small, we can take the ground state BS wave function to be a linear combination of two eigenstates $\mathcal {F}^{10}_{\lambda \tau }(P'\cdot p',p'^2)$ and $\mathcal {F}^{20}_{\lambda \tau }(P'\cdot p',p'^2)$ corresponding to the lowest energy in Eqs. (36) and (37). Then in the basis provided by $\mathcal {F}^{10}_{\lambda \tau }(P'\cdot p',p'^2)=T^1_{\lambda \tau }\mathcal {F}_{10}(P'\cdot p',p'^2)$ and $\mathcal {F}^{20}_{\lambda \tau }(P'\cdot p',p'^2)=T^2_{\lambda \tau }\mathcal {F}_{20}(P'\cdot p',p'^2)$, the BS wave function $\chi ^{0^+}_{\lambda \tau }$ is considered as

$$\begin{aligned} \chi ^{0^+}_{\lambda \tau }(P',p')=c_1\mathcal {F}^{10}_{\lambda \tau }(P'\cdot p',p'^2)+c_2\mathcal {F}^{20}_{\lambda \tau }(P'\cdot p',p'^2). \end{aligned}$$

(38)

Substituting (38) into the BS equation (23) and comparing the tensor structures in both sides, we obtain an eigenvalue equation,

$$\begin{aligned}&c_1\mathcal {F}_{10}(P'\cdot p',p'^2) =\frac{1}{p_1'^2+M_1^2-i\epsilon }\frac{1}{p_2'^2+M_2^2-i\epsilon }\nonumber \\&\quad \times \Bigg \{\int \!\frac{i\mathrm{d}^4q'}{(2\pi )^4}\Bigg \{h_1^{(s)}(k^2)\frac{g_\sigma ^2}{k^2\!+\!m_\sigma ^2}\bar{h}_1^{(s)}(k^2)\nonumber \\&\quad +\Bigg (\frac{g_\rho ^2}{k^2+m_\rho ^2}+\frac{g_1^2}{k^2+m_\omega ^2} +\frac{g_8^2}{k^2+m_\phi ^2}\Bigg )\{h_1^{(\text {v})}(k^2)\bar{h}_1^{(\text {v})}(k^2)\nonumber \\&\quad \times (p_1'+q_1')\cdot (p_2'+q_2') +2h_1^{(\text {v})}(k^2)\bar{h}_2^{(\text {v})}(k^2)\nonumber \\&\quad \times [(q'_1\cdot q'_2)\!-\!(q'_1\cdot p'_2)]+2h_2^{(\text {v})}(k^2)\bar{h}_1^{(\text {v})}(k^2)[(q'_1\cdot q'_2)\nonumber \\&\quad -(p'_1\cdot q'_2)]\}\Bigg \}c_1\mathcal {F}_{10}(P'\cdot q',q'^2)\nonumber \\&\quad +\int \frac{i\mathrm{d}^4q'}{(2\pi )^4}\Bigg (\frac{g_\rho ^2}{k^2+m_\rho ^2}+\frac{g_1^2}{k^2+m_\omega ^2} +\frac{g_8^2}{k^2+m_\phi ^2}\Bigg )\nonumber \\&\quad \times \{2h_1^{(\text {v})}(k^2)\bar{h}_2^{(\text {v})}(k^2) [q_1'^2q_2'^2-q_1'^2(p'_2\cdot q'_2)]\nonumber \\&\quad +2h_2^{(\text {v})}(k^2)\bar{h}_1^{(\text {v})}(k^2)[q_1'^2q_2'^2-q_2'^2(p'_1\cdot q'_1)]\}\nonumber \\&\quad \times c_2\mathcal {F}_{20}(P'\cdot q',q'^2)\Bigg \}, \end{aligned}$$

(39a)

$$\begin{aligned}&c_2\mathcal {F}_{20}(P'\cdot p',p'^2)\nonumber \\&\quad =\frac{1}{p_1'^2+M_1^2-i\epsilon }\frac{1}{p_2'^2+M_2^2-i\epsilon }\Bigg \{\int \frac{i\mathrm{d}^4q'}{(2\pi )^4}\frac{1}{M_1^2p_2'^2}\nonumber \\&\qquad \times \Bigg (\frac{g_\rho ^2}{k^2+m_\rho ^2}+\frac{g_1^2}{k^2+m_\omega ^2} +\frac{g_8^2}{k^2+m_\phi ^2}\Bigg )\nonumber \\&\qquad \times \{h_1^{(\text {v})}(k^2)\bar{h}_2^{(\text {v})}(k^2)[(p'_1\cdot p'_2)(q'_1\cdot q'_2)\nonumber \\&\qquad -(p'_1\cdot q'_2)(q'_1\cdot p'_2)]+h_2^{(\text {v})}(k^2)\bar{h}_1^{(\text {v})}(k^2)\nonumber \\&\qquad \times [p_1'\cdot (p_2'+q_2')q'_2\cdot (q'_1-p_1')\nonumber \\&\qquad -(M_1^2+(p'_1\cdot q'_1))q_2'\cdot (p_2'+q_2')]\}\nonumber \\&\qquad \times c_1\mathcal {F}_{10}(P'\cdot q',q'^2)+\int \frac{i\mathrm{d}^4q'}{(2\pi )^4}\frac{1}{M_1^2p_2'^2}\nonumber \\&\qquad \times \Bigg \{h_1^{(s)}(k^2)\frac{g_\sigma ^2}{k^2+m_\sigma ^2}\bar{h}_1^{(s)}(k^2)q_2'^2[M_1^2\nonumber \\&\qquad +(p_1'\cdot q_1')-q_1'^2]+\Bigg (\frac{g_\rho ^2}{k^2+m_\rho ^2}+\frac{g_1^2}{k^2+m_\omega ^2}\nonumber \\&\qquad +\frac{g_8^2}{k^2+m_\phi ^2}\Bigg )\{h_1^{(\text {v})}(k^2)\bar{h}_1^{(\text {v})}(k^2)(p_1'+q_1')\nonumber \\&\qquad \times \cdot (p_2'+q_2')q_2'^2[M_1^2+(p_1'\cdot q_1')\nonumber \\&\qquad -q_1'^2]+h_1^{(\text {v})}(k^2)\bar{h}_2^{(\text {v})}(k^2)\nonumber \\&\qquad \times [M_1^2(q_1'\cdot q_2')(p_2'\cdot q_2')-M_1^2q_2'^2(p_2'\cdot q_1')\nonumber \\&\qquad +q_1'^2q_2'^2(p_1'\cdot p_2')-q_1'^2(p'_1\cdot q'_2)\nonumber \\&\qquad \times (p'_2\cdot q'_2)]+h_2^{(\text {v})}(k^2)\bar{h}_1^{(\text {v})}(k^2)\nonumber \\&\qquad \times q_2'^2[p_1'\cdot (p_2'+q_2')q_1'\cdot (q_1'-p_1') \nonumber \\&\qquad -(M_1^2+(p_1'\cdot q_1'))q_1'\cdot (p_2'+q_2')]\}\Bigg \}\nonumber \\&\qquad \times c_2\mathcal {F}_{20}(P'\cdot q',q'^2)\Bigg \}, \end{aligned}$$

(39b)

where the eigenvalues are different from the eigenvalues in (36) and (37). From this equation, we can obtain the eigenvalues and eigenfunctions which contain the contribution from the cross terms.

Comparing the terms $(\eta _1\eta _2P'_{\lambda }P'_{\tau }+\eta _2P'_{\lambda }p'_{\tau }-\eta _1p'_{\lambda }P'_{\tau }-p'_{\lambda }p'_{\tau })$ in the left and right sides of Eq. (36), we obtain

$$\begin{aligned}&\mathcal {F}_1(P'\cdot p',p'^2) =\frac{1}{p_1'^2+M_1^2-i\epsilon }\frac{1}{p_2'^2+M_2^2-i\epsilon }\nonumber \\&\quad \times \!\int \frac{i\mathrm{d}^4q'}{(2\pi )^4}V_{1}(p',q';P')\mathcal {F}_1(P'\cdot q',q'^2), \end{aligned}$$

(40)

where $V_{1}(p',q';P')$ contains all coefficients of the term $(\eta _1\eta _2P'_{\lambda }P'_{\tau }+\eta _2P'_{\lambda }p'_{\tau }-\eta _1p'_{\lambda }P'_{\tau }-p'_{\lambda }p'_{\tau })$ in the right side of (36). In this paper, we set $k=(\mathbf{k},0)$. Then the fourth components of momenta of two heavy mesons have no change: $p'_{10}=q'_{10}=E_1(p_1')=E_1(q_1')$, $p'_{20}=q'_{20}=E_2(p_2')=E_2(q_2')$. To simplify the potential, we replace the heavy meson energies $E_1(p_1')=E_1(q_1')\rightarrow E_1=(M^2-M_2^2+M_1^2)/(2M)$, $E_2(p_2')=E_2(q_2')\rightarrow E_2=(M^2-M_1^2+M_2^2)/(2M)$. The potential depends on the three-vector momentum $V(p',q';P')\Rightarrow V(\mathbf{p}',\mathbf q ',M)$. Integrating both sides of Eq. (40) over $p_0'$ and multiplying by $(M+\omega _1+\omega _2)(M^2-(\omega _1-\omega _2)^2)$, we obtain the the Schrödinger type equation

$$\begin{aligned}&\left( \frac{b_1^2(M)}{2\mu _R}-\frac{\mathbf{p}'^2}{2\mu _R}\right) \Psi _1^{0^+}(\mathbf{p}')\nonumber \\&\quad =\int \frac{\mathrm{d}^3k}{(2\pi )^3}V_{1}^{0^+}(\mathbf{p}',\mathbf k )\Psi _1^{0^+}(\mathbf{p}',\mathbf k ), \end{aligned}$$

(41)

and the potential between $D^{*0}$ and $\bar{D}^{*0}$ up to the second order of the $p'/M_H$ expansion

$$\begin{aligned} V_{1}^{0^+}(\mathbf{p}',\mathbf k )&= \frac{h_1^{(s)}(k^2)}{2E_1}\frac{g_\sigma ^2}{k^2+m_\sigma ^2}\frac{\bar{h}_1^{(s)}(k^2)}{2E_2}\nonumber \\&\quad +h_1^{(\text {v})}(k^2)\left( \frac{g_\rho ^2}{k^2\!+\!m_\rho ^2}\!+\!\frac{g_1^2}{k^2\!+\!m_\omega ^2}\!+\!\frac{g_8^2}{k^2\!+\!m_\phi ^2}\right) \nonumber \\&\quad \times \bar{h}_1^{(\text {v})}(k^2)\left[ -1-\frac{4\mathbf{p}'^2+5\mathbf{k}^2}{4E_1E_2}\right] , \end{aligned}$$

(42)

where $\Psi _1^{0^+}(\mathbf{p}')=\int dp'_0F_1(P'\cdot p',p'^2)$, $\mu _R=E_1E_2/(E_1+E_2)=[M^4-(M_1^2-M_2^2)^2]/(4M^3)$, $b^2(M)=[M^2-(M_1+M_2)^2][M^2-(M_1-M_2)^2]/(4M^2)$, $\omega _1=\sqrt{\mathbf{p}'^2+M_1^2}$ and $\omega _2=\sqrt{\mathbf{p}'^2+M_2^2}$. Comparing the terms $(\eta _1 ^2P'_{\lambda }P'_{\tau }+\eta _1P'_{\lambda }p'_{\tau }+\eta _1p'_{\lambda }P'_{\tau }+p'_{\lambda }p'_{\tau })$ in both sides of Eq. (37), we obtain

$$\begin{aligned}&p_2'^2\mathcal {F}_2(P'\cdot p',p'^2)=\frac{1}{p_1'^2+M_1^2-i\epsilon }\frac{1}{p_2'^2+M_2^2-i\epsilon }\nonumber \\&\times \int \frac{i\mathrm{d}^4q'}{(2\pi )^4}V_{2}(p',q';P')q_2'^2\mathcal {F}_2(P'\cdot q',q'^2). \end{aligned}$$

(43)

Setting $\Psi _2^{0^+}(\mathbf{p}')=\int \mathrm{d}p'_0p_2'^2\mathcal {F}_2(P'\cdot p',p'^2)$, we obtain the Schrödinger type equation

$$\begin{aligned}&\left( \frac{b_2^2(M)}{2\mu _R}-\frac{\mathbf{p}'^2}{2\mu _R}\right) \Psi _2^{0^+}(\mathbf{p}')\nonumber \\&\quad =\int \frac{\mathrm{d}^3k}{(2\pi )^3}V_{2}^{0^+}(\mathbf{p}',\mathbf k )\Psi _2^{0^+}(\mathbf{p}',\mathbf k ) \end{aligned}$$

(44)

and the potential between $D^{*0}$ and $\bar{D}^{*0}$ up to the second order of the $p'/M_H$ expansion

$$\begin{aligned} V_{2}^{0^+}(\mathbf{p}',\mathbf k )&= \frac{h_1^{(s)}(k^2)}{2E_1}\frac{g_\sigma ^2}{k^2+m_\sigma ^2}\frac{\bar{h}_1^{(s)}(k^2)}{2E_2}\left[ 1-\frac{\mathbf{k}^2}{M_1^2}\right] \nonumber \\&\quad +h_1^{(\text {v})}(k^2)\left( \frac{g_\rho ^2}{k^2\!+\!m_\rho ^2}\!+\!\frac{g_1^2}{k^2+m_\omega ^2}\!+\!\frac{g_8^2}{k^2\!+\!m_\phi ^2}\right) \nonumber \\&\quad \times \bar{h}_1^{(\text {v})}(k^2)\left[ \!-1\!-\!\frac{2\mathbf{p}'^2+2\mathbf{k}^2}{4M_1^2}-\frac{2\mathbf{p}'^2+2\mathbf{k}^2}{4E_1E_2}\right] \!. \end{aligned}$$

(45)

In instantaneous approximation the eigenfunctions in Eqs. (36) and (37) can be calculated and the eigenvalue equation (39) becomes

$$\begin{aligned} \left( \begin{array}{cc} \frac{b_{10}^2(M)}{2\mu _R}-\lambda &{}H_{12}\\ H_{21}&{}\quad \frac{b_{20}^2(M)}{2\mu _R}-\lambda \end{array} \right) \left( \begin{array}{c} c'_1\\ c'_2 \end{array} \right) =0, \end{aligned}$$

(46)

where we have the matrix elements

$$\begin{aligned} H_{12}=H_{21}&=\int \mathrm{d}^3p'\Psi _{10}^{0^+}(\mathbf{p}')^*\int \frac{\mathrm{d}^3k}{(2\pi )^3}h_1^{(\text {v})}(k^2)\nonumber \\&\quad \times \left( \frac{g_\rho ^2}{k^2+m_\rho ^2}+\frac{g_1^2}{k^2+m_\omega ^2}+\frac{g_8^2}{k^2+m_\phi ^2}\right) \nonumber \\&\quad \times \bar{h}_1^{(\text {v})}(k^2)\frac{\mathbf{k}^2}{E_1E_2}\Psi _{20}^{0^+}(\mathbf{p}',\mathbf k ), \end{aligned}$$

(47)

and $b_{10}^2(M)/(2\mu _R)$ and $b_{20}^2(M)/(2\mu _R)$ are the eigenvalues corresponding to lowest energy in Eqs. (41) and (44), respectively; $\Psi _{10}^{0^+}$ and $\Psi _{20}^{0^+}$ are the corresponding eigenfunctions. In (42), (45), and (47) the contribution from one-$\pi$ exchange to the potential between two heavy vector mesons has vanished, but we still give the heavy meson form factors $h^{(p)}(k^2)$ and $\bar{h}^{(p)}(k^2)$ in Sect. 4. Then applying the method above, we can investigate the alternative $J^P=2^+$ assignment for the Y state.

4 Form factors of heavy vector mesons

To calculate these heavy vector meson form factors $h(k^2)$ describing the heavy meson structure, we have to know the wave function of the heavy vector meson in instantaneous approximation. The heavy vector meson $D^{*0}$ is regarded as a resonance and its three-vector wave function in the rest frame has been given [5]:

$$\begin{aligned}&\Psi ^V(\mathbf{p})=\frac{2\pi i}{N^V}\frac{1}{4\omega _c\omega _u}\nonumber \\&\quad \left\{ \mathrm{exp} \left[ \!\frac{-2\mathbf{p}^2\!-\!M_1^2\!-\!m_c^2\!+\!2M_1\omega _c\!+\!\Gamma ^2/4\!+\!(M_1\!-\! \omega _c)i\Gamma }{\omega _{D^{*0}}^2}\!\right] \right. \nonumber \\&\qquad \times \left[ \frac{-M_1+\omega _c-\omega _u-i\Gamma /2}{(M_1\!-\!\omega _c\!+\!\omega _u)^2+\Gamma ^2/4}\!+\!\frac{M_1\!-\!\omega _c-\omega _u+i\Gamma /2}{(M_1-\omega _c-\omega _u)^2+\Gamma ^2/4}\right] \nonumber \\&\qquad \times \left[ \frac{\mathbf{p}^2}{3}\!+\!\omega _c M_1-\omega _c^2+\Gamma ^2/4 \!+\!m_cm_u\!+\!i\left( \frac{M_1\Gamma }{2}\!-\!\omega _c\Gamma \right) \right] \nonumber \\&\qquad -\mathrm{exp}\left( \frac{-2\mathbf{p}^2-m_u^2}{\omega _{D^{*0}}^2}\right) \left( \frac{\mathbf{p}^2}{3}-\omega _u^2+M_1\omega _u+m_cm_u\right) \nonumber \\&\qquad \times \, \left. \frac{M_1-\omega _c-\omega _u+i\Gamma /2}{(M_1-\omega _c-\omega _u)^2+\Gamma ^2/4}\right\} \sqrt{3}\hat{\mathbf{p}}, \end{aligned}$$

(48)

where $\mathbf{p}$ is the relative momentum between quark and antiquark in the heavy meson, $\hat{\mathbf{p}}$ is the unit momentum, $N^V$ is the normalization, $\omega _{D^{*0}}$=1.81 GeV [12], $\Gamma$ is the full width of resonance, and $\omega _{c,u}=\sqrt{\mathbf{p}^2+m_{c,u}}$ and $m_{c,u}$ are the constituent quark masses.

In this paper, we emphatically introduce the form factors $h^{-}(k^2)$ and $h^{(p)}(k^2)$ derived from one-$\pi$ exchange, while $h^{(s)}(k^2)$ and $h^{(\text {v})}(k^2)$ have been calculated [5]. Firstly, the matrix element of the quark current $J^-=i\bar{u}\gamma _5 u$ between the heavy meson states (H) has the form [13, 14]

$$\begin{aligned}&\langle H(Q)|J^-(0)|H(P) \rangle \nonumber \\&\quad =\int \frac{\mathrm{d}^{3}q\mathrm{d}^{3}p}{(2\pi )^{6}}\bar{\Psi }_{Q}^{H}(\mathbf{q})\Gamma (\mathbf{p},\mathbf q )\Psi _{P}^{H}(\mathbf{p}), \end{aligned}$$

(49)

where $\Gamma (\mathbf{p},\mathbf q )$ is the two-particle vertex function and $\Psi _{Q}^{H}$ is the heavy vector meson wave function boosted to the moving reference frame with momentum Q. In Fig. 3 the vertex function $\Gamma (\mathbf{p},\mathbf q )$ in the impulse approximation is shown. The corresponding vertex function of the meson–quark interaction is given by

$$\begin{aligned} \Gamma ^{(1)}(\mathbf{p},\mathbf q )\!=\!\left\{ \begin{array}{ll} \bar{v}_{\bar{u}}(q_{1})i\gamma _5v_{\bar{u}}(p_{1})(2\pi )^{3}\delta (\mathbf{q}_{2}-\mathbf{p}_{2}) &{}\quad \hbox {for}\,\,\, D^{*0},\\ \bar{u}_{u}(q_{1})i\gamma _5u_{u}(p_{1})(2\pi )^{3}\delta (\mathbf{q}_{2}-\mathbf{p}_{2}) &{}\quad \hbox {for}\,\,\, \bar{D}^{*0}, \end{array} \right. \nonumber \\ \end{aligned}$$

(50)

where $u_u(p)$ and $v_{\bar{u}}(p)$ are the spinors of the quark $u$ and antiquark $\bar{u}$, respectively,

$$\begin{aligned} u_\lambda (p)&= \sqrt{\frac{\epsilon _u(p)+m_u}{2\epsilon _u(p)}} \left( \begin{array}{c} 1 \\ \frac{ \mathbf{\sigma }\cdot \mathbf{p}}{ \epsilon _u(p)+m_u } \end{array} \right) \chi _{\lambda },\nonumber \\ v_\lambda (p)&= \sqrt{\frac{\epsilon _u(p)+m_u}{2\epsilon _u(p)}} \left( \begin{array}{l} \frac{ \mathbf{\sigma }\cdot \mathbf{p}}{ \epsilon _u(p)+m_u} \\ 1 \end{array} \right) \chi _{\lambda }, \end{aligned}$$

(51)

with $\epsilon _{u,c}(p)=\sqrt{\mathbf{p}^{2}+m_{u,c}^{2}}$ and [13, 14]

$$\begin{aligned} p_{1,2}&=\epsilon _{u,c}(p)\frac{P}{M_{H}}\!\pm \!\sum ^{3}_{i=1}n^{(i)}(P)p_{i},\quad M_{H}\!=\! \epsilon _{u}(p)\!+\!\epsilon _{c}(p),\\ q_{1,2}&=\epsilon _{u,c}(q)\frac{Q}{M_{H}}\!\pm \!\sum ^{3}_{i=1}n^{(i)}(Q)q_{i},\quad M_{H}\!=\!\epsilon _{u}(q)\!+\!\epsilon _{c}(q), \end{aligned}$$

and $n^{(i)}$ are three four-vectors defined by

$$\begin{aligned} n^{(i)}(P)&= \left\{ \delta _{ij}+\frac{P_iP_j}{M_{H}[E_{H}(P)+M_{H}]},~i\frac{P_i}{M_{H}} \right\} ,\\ E_{H}(P)&= \sqrt{\mathbf{P}^{2}+M_{H}^{2}}. \end{aligned}$$

In Eq. (50) the first term represents the light pseudoscalar meson interaction with the $u$-antiquark in $D^{*0}$, while the second term represents its interaction with the $u$-quark in $\bar{D}^{*0}$. Substituting the vertex function $\Gamma ^{(1)}$ given by Eq. (50) into the matrix element (49) and then comparing the resulting expressions with the form factor decompositions (28) and (29), we find

$$\begin{aligned} h^{-}(k^2)=\bar{h}^{-}(k^2)=0. \end{aligned}$$

(52)

Fig. 3

The vertex function $\Gamma$ in the impulse approximation. The light meson interaction with $u$-antiquark in $D^{*0}$ and $u$-quark in $\bar{D}^{*0}$ is shown

Then the quark current becomes $J^+_\mu =i\bar{u}\gamma _\mu \gamma _5 u$ and the matrix element between heavy meson states has the form

$$\begin{aligned} \langle H(Q)|J_{\mu }^+(0)|H(P) \rangle \!=\!\int \frac{\mathrm{d}^{3}q\mathrm{d}^{3}p}{(2\pi )^{6}}\bar{\Psi }_{Q}^{H}(\mathbf{q})\Gamma _{\mu }(\mathbf{p},\mathbf q )\Psi _{P}^{H}(\mathbf{p}),\nonumber \\ \end{aligned}$$

(53)

and the corresponding vertex function is

$$\begin{aligned} \Gamma _\mu ^{(1)}(\mathbf{p},\mathbf q )\!=\! \left\{ \begin{array}{ll} \bar{v}_{\bar{u}}(q_{1})i\gamma _\mu \gamma _5 v_{\bar{u}}(p_{1})(2\pi )^{3}\delta (\mathbf{q}_{2}-\mathbf{p}_{2}) &{} \hbox {for}\,\,\, D^{*0},\\ \bar{u}_{u}(q_{1})i\gamma _\mu \gamma _5 u_{u}(p_{1})(2\pi )^{3}\delta (\mathbf{q}_{2}-\mathbf{p}_{2}) &{} \hbox {for}\,\,\, \bar{D}^{*0}. \end{array} \right. \nonumber \\ \end{aligned}$$

(54)

The form factors corresponding to one light pseudoscalar meson exchange are obtained,

$$\begin{aligned} h^{(p)}(k^{2})&=\bar{h}^{(p)}(k^{2})=F_3({\mathbf{k}^{2}}),\nonumber \\ F_3(\mathbf{k}^{2})&=\frac{\sqrt{E_{H}M_{H}}}{E_{H}+M_{H}}\int \frac{\mathrm{d}^{3}p}{(2\pi )^{3}}\bar{\Psi }^{V}\left( \mathbf{p}+\frac{2\epsilon _c(p)}{E_{H}+M_{H}}\mathbf{k}\right) \nonumber \\&\quad \times \sqrt{\frac{\epsilon _u(p+k)+m_u}{2\epsilon _u(p+k)}}\sqrt{\frac{\epsilon _u(p)+m_u}{2\epsilon _u(p)}}\nonumber \\&\quad \times \frac{\mathbf{pk}}{(\epsilon _u(p+k)+m_u)(\epsilon _u(p)+m_u)} \Psi ^{V}(\mathbf{p}), \end{aligned}$$

(55)

where $\Psi ^{V}$ is the wave function of the heavy vector meson expressed as Eq. (48). The function $F_{3}(\mathbf{k}^{2})$ is shown in Fig. 4.

Fig. 4

The form factor for the vertex of heavy vector meson $D^{*0}$ coupling to $\pi$ meson

Finally, we obtain the potentials between two heavy vector mesons for $J^P=0^+$,

$$\begin{aligned} V_{1}^{0^+}(\mathbf{p}',\mathbf k )&= -F_1(\mathbf{k}^2)\frac{g_\sigma ^2}{k^2+m_\sigma ^2}F_1(\mathbf{k}^2)\nonumber \\&\quad -F_2(\mathbf{k}^2)\left( \frac{g_\rho ^2}{k^2\!+\!m_\rho ^2}\!+\!\frac{g_1^2}{k^2\!+\!m_\omega ^2}\!+\!\frac{g_8^2}{k^2\!+\!m_\phi ^2}\right) \nonumber \\&\quad \times F_2(\mathbf{k}^2)\left[ 1+\frac{4\mathbf{p}'^2+5\mathbf{k}^2}{4E_1E_2}\right] ,\nonumber \\ V_{2}^{0^+}(\mathbf{p}',\mathbf k )&= -F_1(\mathbf{k}^2)\frac{g_\sigma ^2}{k^2+m_\sigma ^2}F_1(\mathbf{k}^2)\left[ 1-\frac{\mathbf{k}^2}{M_1^2}\right] \nonumber \\&\quad -F_2(\mathbf{k}^2)\left( \frac{g_\rho ^2}{k^2+m_\rho ^2}\!+\!\frac{g_1^2}{k^2+m_\omega ^2}\!+\!\frac{g_8^2}{k^2+m_\phi ^2}\right) \nonumber \\&\quad \times F_2(\mathbf{k}^2)\left[ 1+\frac{2\mathbf{p}'^2+2\mathbf{k}^2}{4M_1^2}+\frac{2\mathbf{p}'^2+2\mathbf{k}^2}{4E_1E_2}\right] , \end{aligned}$$

(56)

where $F_1(\mathbf{k}^2)$ and $F_2(\mathbf{k}^2)$ represent the form factors corresponding to one light scalar and vector meson exchange, respectively, which have been given in our previous work [5].

5 Numerical result

We have the constituent quark masses $m_{c}=1.55$GeV, $m_{u}=0.33$GeV, the meson masses $m_{\sigma }=0.46$GeV, $m_{\rho }=0.775$GeV, $m_{\omega }=0.782$GeV, $m_{\phi }=1.019$GeV, $m_{D^{*0}}=m_{\bar{D}^{*0}}=2.007$GeV, and the full width of the heavy vector meson $\Gamma _{D^{*0}}=0.002$GeV [15]. Equations (41) and (44) can be solved numerically with these potentials in Eq. (56), and then the eigenvalue equation (46) can be solved. Using the same method, we investigate the molecule state $D^{*0}\bar{D}^{*0}$ with $J^P=2^+$. Additionally, we investigate the molecule states consisting of two heavy vector mesons $B^{*0}\bar{B}^{*0}$, which are composed of bottom quark and $d$-quark. Then we have the constituent quark masses $m_{b}=4.88$GeV, $m_{d}=0.33$GeV, the meson masses $m_{B^{*0}}=m_{\bar{B}^{*0}}=5.325$GeV, the width $\Gamma _{B^{*0}}=0.015$ keV, and $\omega _{B^{*0}}=\omega _{\bar{B}^{*0}}=1.81$GeV [12]. Table 1 shows our results for the masses of these molecule states.

Table 1 Masses of charmed and bottom meson molecule states (in GeV)

Varying the constituent quark masses $m_u$, $m_c$, $m_d$, $m_b$, and the full widths of the heavy vector mesons $\Gamma _{D^{*0}}$, $\Gamma _{B^{*0}}$ within 5% simultaneously, we find that the ratio of the numerical result difference dependent on these parameters and the binding energy is at most 5%. Then in our approach the calculated molecule state masses depend on these parameters, but not sensitively.

For the molecule state $D^{*0}\bar{D}^{*0}$ with $J^P=0^+$, we obtain two solutions from Eq. (46). The lower energy should be the ground state mass of this molecule state, which lies below the threshold, and the calculated mass is consistent with the experimental data, while in the experiment the mass of Y(3940) is $3.943$GeV [1]. This result is different from Ref. [5]; this is because in this paper we consider the SU(3) symmetry. At the same time, the molecule state $D^{*0}\bar{D}^{*0}$ with $J^P=2^+$ lies above the threshold. Therefore, we can draw the conclusion that if the Y(3940) state is a molecule state composed of $D^{*0}\bar{D}^{*0}$, its quantum numbers should be $J^P=0^+$. Besides, we can predict that two bottom mesons $B^{*0}\bar{B}^{*0}$ can be bound by one light meson exchange as a molecule state with $J^P=0^+$.

6 Conclusion

In this work, we assume that the exotic state Y(3940) is a $D^{*0}\bar{D}^{*0}$ molecule state and calculate its mass. The revised general formalism of the BS wave functions for the bound states composed of two vector fields is applied to investigate this issue. Considering one-$\pi$ exchange and SU(3) symmetry breaking, we construct the interaction potential between $D^{*0}$ and $\bar{D}^{*0}$ through the heavy vector meson form factors describing the heavy meson structure. The calculated mass of the molecule state with $J^P=0^+$ is consistent with the mass of the Y state in experiment, so we conclude that if the Y(3940) state is a molecule state composed of $D^{*0}\bar{D}^{*0}$, its quantum numbers should be $J^P=0^+$. Adopting this method, we investigate the molecule states composed of two bottom mesons.