Skip to main content
SpringerLink
Log in

Correction to the leading term of asymptotics in the problem of counting the number of points moving on a metric tree

  • Published:
Russian Journal of Mathematical Physics Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

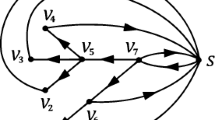
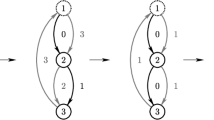
In the problem of determining the asymptotics for the number of points moving along a metric tree, a polynomial approximation that uses Barnes’ multiple Bernoulli polynomials is found. The connection between the second term of the asymptotic expansion and the graph structure is discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. L. Chernyshev and A.A. Tolchennikov, “Asymptotic Estimate for the Counting Problems Corresponding to the Dynamical System on Some Decorated Graphs,” Ergodic Theory and Dynamical Systems, Cambridge University Press, 1–12 (2017), DOI:10.1017/etds.2016.102.

    Google Scholar 

  2. V. L. Chernyshev and A. I. Shafarevich, “Statistics of Gaussian Packets on Metric and Decorated Graphs,” Philosophical Transactions of the Royal Society A. 372 (2007), Article number: 20130145 (2014), DOI: 10.1098/rsta.2013.0145.

  3. B. Borda, “Lattice Points in Algebraic Cross-Polytopes and Simplices,” Working papers by Series math-ph ”arxiv.org”./2016/08. arXiv:1608.02417 [math.NT], pp. 27 (2016).

    Google Scholar 

  4. V. L. Chernyshev and A.A. Tolchennikov, “How the Permutation of Edges of a Metric Graph Affects the Number of Points Moving Along the Edges,” Working papers by Series math-ph ”arxiv.org”./2014/10. No.1410.5015. http://arxiv.org, pp. 12 (2014).

    Google Scholar 

  5. V. L. Chernyshev, “Time-dependent Schrödinger equation: statistics of the distribution of Gaussian packets on a metric graph,” Trudy Mat. Inst. Steklova 270, 249–265 (2010) [Proc. Steklov Inst. Math. 270, 246–262 (2010)].

    MATH  Google Scholar 

  6. V. L. Chernyshev, A.A. Tolchennikov, and A. I. Shafarevich, “Behavior of Quasi-Particles on Hybrid Spaces. Relations to the Geometry of Geodesics and to the Problems of Analytic Number Theory,” Regular and Chaotic Dynamics 21 (5), 531–537 (2016).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. G. Berkolaiko, “Quantum Star Graphs and Related Systems,” PhD Thesis, University of Bristol, pp. 135 (2000).

    Google Scholar 

  8. D. C. Spencer, “The Lattice Points of Tetrahedra,” J. Math. Phys. Mass. Inst. Tech. 21, (1942), 189–197; doi: 10.1002/sapm1942211189.

    MathSciNet  MATH  Google Scholar 

  9. D. H. Lehmer, “The Lattice Points of an n-Dimensional Tetrahedron,” Duke Math. J. 7 (1), 341–353 (1940).

    Article  MathSciNet  MATH  Google Scholar 

  10. N. E. Nørlund, Vorlesungen über Differenzenrechnung Berlin: Springer-Verlag, 1924..

    Book  MATH  Google Scholar 

  11. E.W. Barnes, “On the Theory of the Multiple Gamma Function,” Trans. Cambridge Philos. Soc. 19, 374–425 (1904).

    Google Scholar 

  12. G. H. Hardy and M. Riesz, The General Theory of Dirichlet’s Series (Cambridge Tracts in Mathematics and Mathematical Physics), No. 18, Reink Books, 2017..

  13. A. Barvinok, Integer Points in Polyhedra (European Mathematical Society, Zürich), 2008..

    Book  MATH  Google Scholar 

  14. F. Beukers, “The Lattice-Points of n-Dimensional Tetrahedra,” Indag. Math. 37, 365–372 (1975).

    Article  MathSciNet  MATH  Google Scholar 

  15. V. I. Danilov, “The geometry of toric varieties,” Uspekhi Mat. Nauk 33 (2 (200)), 85–134 (1978) [Russian Math. Surveys, 33:2 (1978), 97–154].

    MathSciNet  MATH  Google Scholar 

  16. A. V. Pukhlikov and A. G. Khovanskii, “The Riemann–Roch Theorem for Integrals and Sums of Quasipolynomials on Virtual Polytopes,” Algebra Analiz 4 (4), 188–216 (1992) [St. Petersburg Math. J. 4 (4), 789–812 (1993)].

    MathSciNet  MATH  Google Scholar 

  17. L. Carlitz, “Note on Nørlund’s Polynomial B n(z),” Proceedings of the American Mathematical Society 11 (3), 452–455 (1960).

    MathSciNet  MATH  Google Scholar 

  18. J. A. Todd, “The Arithmetical Invariants of Algebraic Loci,” Proc. London Math. Soc. 43 (1), 190–225 (1937).

    MathSciNet  MATH  Google Scholar 

  19. M. Beck and A. Bayad, “Relations for Bernoulli–Barnes Numbers and Barnes Zeta Functions,” International Journal of Number Theory 10, 1321–1335 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  20. F. Hirzebruch, Topological Methods in Algebraic Geometry, Classics in Mathematics (Translation from the German and appendix one by R. L. E. Schwarzenberger. Appendix two by A. Borel. Springer, 1978. 234 p).

    Google Scholar 

  21. W. M. Schmidt, “Simultaneous Approximation to Algebraic Numbers by Rationals”, Acta Math. 125, 189–201 (1970).

    Article  MathSciNet  MATH  Google Scholar 

  22. R. Diaz, Q-N. Le, and S. Robins, “Fourier Transforms of Polytopes, Solid Angle Sums, and Discrete Volume”, arXiv:1602.08593 [math.CO], 2016. 14 p.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. National Research University Higher School of Economics, Moscow, Russia

    V. L. Chernyshev

  2. Lomonosov Moscow State University, Moscow, Russia

    A. A. Tolchennikov

  3. Ishlinsky Institute for Problems in Mechanics of the Russian Academy of Sciences, Moscow, Russia

    A. A. Tolchennikov

  4. Moscow Institute of Physics and Technology (State University), Dolgoprudny, Moscow Region, Russia

    A. A. Tolchennikov

Authors
  1. V. L. Chernyshev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. A. Tolchennikov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. L. Chernyshev.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chernyshev, V.L., Tolchennikov, A.A. Correction to the leading term of asymptotics in the problem of counting the number of points moving on a metric tree. Russ. J. Math. Phys. 24, 290–298 (2017). https://doi.org/10.1134/S1061920817030025

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1061920817030025

Search

Navigation