Abstract
Catastrophic risks are often characterised by a low probability, a high severity and a large number of affected individuals. Taking these specificities into account, we analyse the capacity of insurance contracts to provide coverage for those risks, independently from the market failures frequently observed in practice. On the demand side, we characterise individual preferences under which the willingness to pay for the coverage of large losses remains significant, although their occurrence probability is very small. On the supply side, the correlation between individual losses affects the insurance pricing through the insurers’ cost of capital. Analysing the interaction between demand and supply yields the key determinants of insurability and of a socially optimal risk sharing strategy.

Source ©2019 Munich Re, Geo Risks Research, NatCatSERVICE. As of November 2019

Similar content being viewed by others
Change history
22 February 2023
A Correction to this paper has been published: https://doi.org/10.1057/s10713-023-00082-5
Notes
The classification follows Munich Re NatCat Service and is based on the World Bank’s Gross National Income (GNI) measure. Countries with GNI below 1045 US dollars are classified as low income and countries with GNI above 12,736 US dollars are classified as high income. Other countries are considered medium income.
Important aspects of the US N.F.I.P. are illustrative of this approach, by facilitating the underwriting of flood policies, (e.g. the “write your own policy”), and through ground intervention of F.E.M.A agents in the case of a flood.
We have \(\varepsilon (w) = w/{\mathbb {E}}{\tilde{\ell }}\) and \(\varepsilon (x) \rightarrow + \infty\) when \(x \rightarrow w-{\bar{L}}\). Hence, the monotonicity assumption made in the proposition guarantees \(\varepsilon (x) > w/{\mathbb {E}}{\tilde{\ell }}\) for all x. If this monotonicity assumption is not made, Proposition 2 holds under \({\bar{\gamma }} < \min \{\varepsilon (x),x \in [w-{\bar{L}},w]\}\).
For the sake of numerical illustration, consider the case of a large-scale nuclear disaster that may occur with probability \(p=10^{-5}\), with expected total losses of $100b evenly spread among 1 million inhabitants (think of people living in the neighbourhood of the nuclear plant). In the case of an accident, each inhabitant would suffer a loss of expected value \({\mathbb {E}}{\tilde{\ell }}=\$100,000\). The unconditional expected loss \(p{\mathbb {E}}{\tilde{\ell }}\) equals $1, and the certainty equivalent is less than \(1+2\theta<\) $3 or \(1+3\theta<\) $4, which is negligible, say as a proportion of their annual electricity expenses. Assuming larger but still realistic values of the index of relative risk aversion would not substantially affect this conclusion. If we assume \(w = \$2M\), then the condition \({\bar{\gamma }} \le w/{\mathbb {E}}{\tilde{\ell }}\) is written as \({\bar{\gamma }} \le 20\).
Note that R(x) is increasing in the HARA case, and assuming \(R(x)>1\) when x is large requires \(\gamma >1\).
Indeed, if the individual prefers full coverage to no coverage, extending his opportunity set does not make him switch to zero coverage. It is easy to check that the optimal limit cover (denoted \(I^*\) below) is positive when \(d(0_+,L)<[u'(w-L)-u'(w)]/u'(w)\) and that this condition is implied by \(\theta (0_+,L)L\ge d(0_+,L)\).
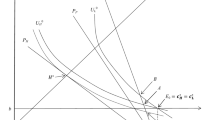
Section 4 will be dedicated to analysing the supply side of the market and will derive a pricing function.
See Schlesinger (2013).
When \(\pi >0\), this corresponds to the degenerate case where the catastrophe may be completely harmless. Only two events are then relevant : either there is a catastrophe that affects all individuals, either nobody suffers a loss, hence the perfect correlation.
In an economy with complete financial markets, \(D = {\mathbb {E}}{\tilde{y}} + \text{ cov }({\tilde{y}},\frac{u'({\tilde{z}})}{{\mathbb {E}}u'({\tilde{z}})})\) defines the price of the asset \({\tilde{y}}\) (see Gollier 2004). Without loss of generality, we use the normalisation \({\mathbb {E}}u'({\tilde{z}}) = 1\).
Note that the right-hand side of (14) depends on \(\pi , L\) and on the distribution of \({\tilde{\kappa }}\). In what follows, L and \({\tilde{\kappa }}\) are considered as given and we analyse the effect of a change in the probability of a catastrophe \(\pi\), that affects the individual probability \(p=\mu _{\kappa } \pi\) of being a victim.
When we consider economies that differ through the value of \(\pi\), we maintain the normalising assumption \({\mathbb {E}}u'({\tilde{z}}) = 1\) for the economy. The utility functions therefore depend on \(\pi\) and \(u'(w) \rightarrow 1\) when \(\pi \rightarrow 0\) for any random variable \({\tilde{\kappa }}\).
Equation (19) is an approximation of \(\psi (0)\) by default when \(u'''>0\) that would lead to over-estimate the coverage rates. Numerical simulations, not reported here for the sake of brevity but available from the authors upon request, show that approximating the true price with (19) produces reasonable levels of errors (a few percentage points) for the calibrations considered in the next section.
This restriction on the size of the catastrophe need not be as restrictive as it seems. For example, the Japanese government expects the total cost of the Fukushima-Daiichi accident in 2011 to amount to a 177 billion euros bill. An important part of this cost is systemic since it affects many people at once, but its size, when compared to a 4300 billion euros annual GDP, remains limited.
Considering higher levels of loss probability would indeed give rise to higher errors. Considering \(\pi = 0.1\) instead of \(\pi =0.01\) for, would results in approximation errors lower than \(8.55\%\) and lower than \(2\%\) in 17 out of the 20 scenarios of Table 1.
In addition, large catastrophes often affect people with sometimes widely different (but small) probabilities. Our result suggests that such differences in risk exposure may actually result in very limited differences in optimal coverage values. Similarly, conflicting expert opinions concerning the true probability of a catastrophe would also be irrelevant for the choice of an optimal level of coverage, as long as experts agree that the probability \(\pi\) is very small.
References
Arrow, K.J. 1963. Liquidity preference, lecture vi in” lecture notes for economics 285, the economics of uncertainty”, 33–53. undated, Stanford University.
Barro, R.J. 2006. Rare disasters and asset markets in the twentieth century. The Quarterly Journal of Economics 121 (3): 823–866.
Charpentier, A., and B. Le Maux. 2014. Natural catastrophe insurance: How should the government intervene? Journal of Public Economics 115: 1–17.
Cummins, J.D., N. Doherty, and A. Lo. 2002. Can insurers pay for the “big one”? measuring the capacity of the insurance market to respond to catastrophic losses. Journal of Banking & Finance 26: 557–583.
Eeckhoudt, L., C. Schieber, and T. Schneider. 2000. Risk aversion and the external cost of a nuclear accident. Journal of Environmental Management 58 (2): 109–117.
Farhi, E., and X. Gabaix. 2015. Rare disasters and exchange rates. The Quarterly Journal of Economics 131 (1): 1–52.
Froot, K.A. 2001. The market for catastrophe risk: A clinical examination. Journal of Financial Economics 60 (2): 529–571.
Gollier, C. 1995. The comparative statics of changes in risk revisited. Journal of Economic Theory 66 (2): 522–535.
Gollier, C. 2004. The economics of risk and time. Cambridge: MIT Press.
Gourio, F. 2012. Disaster risk and business cycles. American Economic Review 102 (6): 2734–66.
Grislain-Letrémy, C. 2018. Natural disasters: Exposure and underinsurance. Annals of Economics and Statistics/Annales d’Économie et de Statistique 129: 53–83.
Hertwig, R., G. Barron, E.U. Weber, and I. Erev. 2004. Decisions from experience and the effect of rare events in risky choice. Psychological Science 15 (8): 534–539.
Ikefuji, M., R.J. Laeven, J.R. Magnus, and C. Muris. 2015. Expected utility and catastrophic consumption risk. Insurance: Mathematics and Economics 64: 306–312.
Jaffee, D.M., and T. Russell. 1997. Catastrophe insurance, capital markets, and uninsurable risks. Journal of Risk and Insurance 64: 205–230.
Kousky, C., and R. Cooke. 2012. Explaining the failure to insure catastrophic risks. The Geneva Papers on Risk and Insurance-Issues and Practice 37 (2): 206–227.
Kousky, C., E.O. Michel-Kerjan, and P. Raschky. 2013. Does federal disaster assistance crowd out private demand for insurance, 10. Risk Management and Decision Processes Center, The Wharton School, University of Pennsylvania.
Kunreuther, H. 1973. Recovery From Natural Disasters: Insurance or Federal Aid?. Washington.
Kunreuther, H., N. Novemsky, and D. Kahneman. 2001. Making low probabilities useful. Journal of Risk and Uncertainty 23 (2): 103–120.
Kunreuther, H., and P. Slovic. 1978. Economics, psychology, and protective behavior. The American Economic Review 68 (2): 64–69.
Mossin, J. 1968. Aspects of rational insurance purchasing. The Journal of Political Economy 76: 553–568.
Niehaus, G. 2002. The allocation of catastrophe risk. Journal of Banking & Finance 26 (2–3): 585–596.
Pratt, J.W. 1964. Risk aversion in the small and in the large. Econometrica 32: 122–136.
Raschky, P.A., R. Schwarze, M. Schwindt, and F. Zahn. 2013. Uncertainty of governmental relief and the crowding out of flood insurance. Environmental and Resource Economics 54 (2): 179–200.
Raviv, A. 1979. The design of an optimal insurance policy. The American Economic Review 69 (1): 84–96.
Rietz, T.A. 1988. The equity risk premium a solution. Journal of Monetary Economics 22 (1): 117–131.
Rothschild, M., and J.E. Stiglitz. 1971. Increasing risk ii: Its economic consequences. Journal of Economic Theory 3 (1): 66–84.
Schlesinger, H. 2013. The theory of insurance demand. In Handbook of insurance, ed. G. Dionne, 167–184. New York: Springer.
Weitzman, M.L. 2009. On modeling and interpreting the economics of catastrophic climate change. The Review of Economics and Statistics 91 (1): 1–19.
Zanjani, G. 2002. Pricing and capital allocation in catastrophe insurance. Journal of Financial Economics 65 (2): 283–305.
Acknowledgements
Alexis Louaas gratefully acknowledges the financial support of the EIT Climate-KIC. EIT Climate-KIC is supported by EIT, a body of the European Union. Pierre Picard gratefully acknowledges the financial support of the Labex ECODEC
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare they have no conflict of interest.
Additional information
The original online version of this article was revised due to corrections in equation 1, propositions 1&2, the proofs of propositions 1&2 and corollary 2.
Appendix: Proofs
Appendix: Proofs
1.1 Proof of Proposition 1
We have
Since
for all \(x\in [w-{\bar{L}},w]\), we may write
and thus,
Integrating by parts three times and making the change of variable \(x = w-\ell\) gives
Using
completes the first part of the proof. Integrating by parts twice then gives
hence
1.2 Proof of Corollary 1
The corollary follows straightforwardly from
1.3 Proof of Proposition 2
Let \(\nu (x) = x - w + {\bar{L}} - \int _{w-x}^{{\bar{L}}}{F(\ell ) {\text{d}}\ell }> 0\) for all \(x \in [w-{\bar{L}},w]\), with \(\nu (w) = {\bar{L}} - \int _0^{{\bar{L}}}{F(\ell ){\text{d}}\ell } = {\mathbb {E}}{\tilde{\ell }}\) and \(f'({\bar{L}})<0\). Equation (23) is therefore written as
Hence
\({\text{d}}[\nu (x) u'(x)]/{\text{d}}x >0\) if \(\varepsilon (x) \equiv \frac{\nu '(x)x}{\nu (x)}>R(x)\), and
Since \({\mathbb {E}}{\tilde{\ell }} = {\bar{L}} - \int _0^{{\bar{L}}}{F(\ell ){\text{d}}\ell }\), we have \(\varepsilon (w) = w/{\mathbb {E}}{\tilde{\ell }}\). Assuming \(f(\ell )\rightarrow 0\) when \(\ell \rightarrow {\bar{L}}\) and \(f'({\bar{L}}) < 0\) and applying L’Hôpital’s rule twice, we obtain \(\varepsilon (x) \rightarrow +\infty\) when \(x\rightarrow w-{\bar{L}}\). Assuming that \(\varepsilon (x)\) is monotonic, and therefore decreasing, implies
A sufficient condition for \({\text{d}}[\nu (x) u'(x)]/{\text{d}}x >0\) is therefore
where \({\bar{\gamma }} = \max \{R(x),x\in [w-{\bar{L}},w]\}\). In this case, we have
and consequently
Let \({\bar{A}} = 1/\bar{L}\int _{w-{\bar{L}}}^w{A(x){\text{d}}x}\). We then obtain
Using \(C_{p}^{\prime \prime }<0\) and \(C (0_+,{\tilde{\ell }})=0\) with Eq. (1) allows us to write
1.4 Proof of Corollary 3
A simple calculation shows that Proposition 1 and Corollary 1 can be re-written as
Corollary 4
When \({\tilde{\ell }} =L\) with probability 1, we have
where
and
Using Lemma 1 then shows that
is a sufficient condition for insurance take-up to be positive. If R(x) is non-decreasing, then
Noticing that \(\lim _{L\rightarrow w}{\psi (L)} = \lim _{x\rightarrow 0}{R(x)}\) provides the result.
1.5 Coefficient of correlation \(\rho\)
Let \({\tilde{L}}_i\) and \({\tilde{L}}_j\) be two random variables that represent the losses of individuals i and j. Conditionally on a realisation \(\kappa\) of the random variable \({\tilde{\kappa }}\), losses are assumed identically and independently distributed, hence
As a consequence \({\mathbb {E}}(\tilde{L_i} \tilde{L_j}|\kappa ) = L^2 \pi \kappa ^2\) and \({\mathbb {E}}(\tilde{L_i} \tilde{L_j}) = L^2 \pi {\mathbb {E}}{\tilde{\kappa }}^2\). Similarly,
for all i, hence \({\mathbb {E}}\tilde{L_i} = L\pi \mu _{\kappa }\) and \({\mathbb {E}}\tilde{L_i} {\mathbb {E}}\tilde{L_j}= (L\pi \mu _{\kappa })^2\). The co-variance between two losses is therefore written as
Also, since
implies \({\mathbb {E}}(\tilde{L_i}^2) = \pi L^2 \mu _{\kappa }\), we find the variance of \(\tilde{L_i}\)
Since \(\text{ Var }(\tilde{L_i}) = \text{ Var }(\tilde{L_j})\) for all i, the coefficient of correlation is finally equal to
where the last line is obtained using \(\sigma ^2_{\kappa } = {\mathbb {E}}{\tilde{\kappa }}^2 - \mu _{\kappa }^2\).
1.6 Proof of Proposition 4
When \(\lambda =0\), inequality (16) is rewritten as
Since \(u''<0\), we have
and hence
which gives (24). (16) also holds when \(\lambda\) is not too large.
1.7 Proof of Proposition 5
Using Proposition 3 with Eqs. (16) and (19) gives \(I^*>0\) if
where \(x(L,\lambda ,\rho ) \equiv (1+\lambda )(1 + A(w)L \rho )\). Using \(u'(w) = 1\), we obtain \(\varphi (0) = u'(w) - x(0,\lambda ,\rho ) = - \lambda <0\), and
The function \(\varphi (L)\) is therefore convex with \(\varphi (0)<0\) and \(\varphi ({\bar{L}})>0\) if \(u'(w-{\bar{L}}) > (1+\lambda )[1 + A(w) {\bar{L}} \rho ]\). \(\varphi (L) = 0\) hence defines \({\underline{L}}(\lambda ,\rho )\) with \({\bar{L}}(\lambda , \rho )=0\) if \(\lambda =0\) and \({\bar{L}}(\lambda , \rho )>0\) if \(\lambda >0\). When \(L>{\underline{L}}(\lambda ,\rho )\), (i.e. \(I^*>0\)), Equation (17) gives
for given values of \(\lambda\) and \(\rho\). Let \(z(L) = u'^{-1}(x(L))\). Since DARA implies \(u'''>0\), \(u'^{-1}\) is decreasing and convex and since x(L) is linear, z(L) is also decreasing and convex. From (25), we obtain
Using \(w>=z(0)\) and the convexity of function z(L) yields
which gives \(\partial \beta ^*/\partial L >0\) when \(L\ge {\bar{L}}(\lambda , \rho )\). The comparative statics \(\partial \beta ^*/\partial \rho < 0\) and \(\partial \beta ^*/\partial \lambda < 0\) are obtained by noticing that an increase in either \(\lambda\) or \(\rho\) translates into an increase in x(L). \(u'^{-1}\) decreasing then provides the results.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Louaas, A., Picard, P. Optimal insurance coverage of low-probability catastrophic risks. Geneva Risk Insur Rev 46, 61–88 (2021). https://doi.org/10.1057/s10713-020-00049-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1057/s10713-020-00049-w