Tight bounds on the mutual coherence of sensing matrices for Wigner D-functions on regular grids

Abstract

Many practical sampling patterns for function approximation on the rotation group utilizes regular samples on the parameter axes. In this paper, we analyze the mutual coherence for sensing matrices that correspond to a class of regular patterns to angular momentum analysis in quantum mechanics and provide simple lower bounds for it. The products of Wigner d-functions, which appear in coherence analysis, arise in angular momentum analysis in quantum mechanics. We first represent the product as a linear combination of a single Wigner d-function and angular momentum coefficients, otherwise known as the Wigner 3j symbols. Using combinatorial identities, we show that under certain conditions on the bandwidth and number of samples, the inner product of the columns of the sensing matrix at zero orders, which is equal to the inner product of two Legendre polynomials, dominates the mutual coherence term and fixes a lower bound for it. In other words, for a class of regular sampling patterns, we provide a lower bound for the inner product of the columns of the sensing matrix that can be analytically computed. We verify numerically our theoretical results and show that the lower bound for the mutual coherence is larger than Welch bound. Besides, we provide algorithms that can achieve the lower bound for spherical harmonics.

1 Introduction

In many applications, the goal is to recover a function defined on a group, say on the sphere $\mathbb {S}^2$ and the rotation group $\mathrm {SO}(3)$, from only a few samples [7,8,9,10, 27]. This problem can be seen as a linear inverse problem with structured sensing matrices that contain samples of spherical harmonics and Wigner D-functions.

In the area of compressed sensing and sparse signal recovery, there are recovery guarantee results for random sampling patterns [9, 27] based on proving Restricted Isometry Property (RIP) of the corresponding sensing matrix. Regular deterministic sampling patterns are, however, more prevalent in practice due to their easier deployment [7, 8]. RIP based results cannot be used for analyzing deterministic sensing matrices, because it has been shown in [6, 33] that verifying RIP is computationally hard. For deterministic sampling patterns, the mutual coherence is widely used as a performance indicator, which measures the correlation between different columns in the sensing matrix. For the case of sparse recovery on $\mathbb {S}^2$ and $\mathrm {SO}(3)$, the product of two Wigner D-functions and the product of two spherical harmonics appear in the coherence analysis.

The product of orthogonal polynomials, i.e., Legendre and Jacobi polynomials, is sought-after in mathematics, and it is related to hypergeometric functions. Several works to obtain a closed-form and simplified version of these products have been presented, for instance in [3, 4, 12, 16, 17]. In those articles, the authors attempt to derive a compact formulation of the product and represent it as a linear combination of a single orthogonal polynomial with some coefficients. This representation reveals interesting properties that can also be applied in quantum mechanics [14, 30], geophysics [32], machine learning [24], and low-coherence sensing matrices [7, 8, 10]. In quantum mechanics, these coefficients are used to calculate the addition of angular momenta, i.e., the interaction between two charged particles, and such coefficients are called the Clebsch–Gordan coefficients or Wigner 3j symbols. Specifically, these coefficients appear when we want to determine the product of Wigner D-functions and spherical harmonics. Since Jacobi and Legendre polynomials are specifically used to express the Wigner D-functions and spherical harmonics, the product of those polynomials in terms of Wigner 3j symbols is also commonly used in angular momentum literature [14, 30]. The product of spherical harmonics also emerges in the spatiospectral concentration or Slepian’s concentration problem on the sphere, as discussed in [32]. In this case, the goal is to maximize the concentration of spectrum frequencies, i.e., spherical harmonic coefficients, given a certain area on the spherical surface. The problem is similar to finding relevant eigenvalues from a matrix that consists of the product of spherical harmonics. As a consequence, Wigner 3j symbols appear as a tool to analyze the problem. In the area of machine learning, Wigner D-functions are used for analyzing group transformations of the input to neural networks and to implement equivariant architectures for rotations. The authors in [24] develop Clebsch–Gordan nets to generalize and to improve the performance of spherical convolutional neural networks for recognizing the rotation of spherical images, 3D shape, as well as predicting energy of the atom. The contribution of this article includes the implementation of Wigner D-functions to perform the transformation of a signal in the Fourier domain and to tailor a representation of the product in terms of Clebsch–Gordan coefficients that will primarily support theoretical analysis of the networks.

In this work, we are interested in coherence analysis and sparse recovery tasks. It has been shown in [8] that a wide class of modular symmetric regular sampling patterns, like equiangular sampling, yield highly coherent sensing matrices and thereby perform poorly for signal recovery tasks. Besides, the coherence was shown to be affected by the choice of elevation sampling pattern independent of azimuth and polarization sampling patterns. It was numerically shown that for regular sampling points on the elevation for Wigner D-functions and spherical harmonics, the mutual coherence is lower bounded by the inner product of columns with zero orders and two largest degrees,¹ which are then equal to Legendre polynomials. This bound is not contrived because one can show that this bound is achievable by optimizing azimuth angle $\phi \in [0, 2\pi )$. Consequently, the resulting deterministic sampling points can be implemented into a real-system to carry out measurements on the spherical surface, as discussed in [10, 11]. In this article, we confirm mathematically the numerical findings of [8]. Our proof relies on using results for angular momentum analysis in quantum mechanics and properties of Wigner 3j symbols. To the best of our knowledge, this work is the first to provide the coherence analysis of a sensing matrix using the tools from angular momentum in quantum mechanics.

1.1 Related works

The construction of sensing matrices from a set of orthogonal polynomials is widely studied in the area of compressed sensing. For instance, in [28] the authors show that the sensing matrix construction from random samples of Legendre polynomials with respect to Chebyshev measure fulfils the RIP condition and thus performs a robust and stable recovery guarantee to reconstruct sparse functions in terms of Legendre polynomials by using $\ell _1$-minimization algorithm. The extensions for random samples spherical harmonics and Wigner D-functions are discussed in [8, 9, 27, 29]. The key idea in those articles bears a strong resemblance to the technique discussed in Legendre polynomials’ case, which is based on carefully choosing random samples with respect to different probability measures and preconditioning techniques to keep the polynomials uniformly bounded. Despite the recovery guarantees with regard to the minimum number of samples, it has been discussed in [19] that these theoretical results are seemingly too pessimistic. Practically, one can consider a smaller number of samples and still achieve a very good reconstruction by using $\ell _1$-minimization algorithm. Therefore, a gap between theoretical and practical settings exists. Another concern in the antenna measurement system is designing a smooth trajectory for robotic arms to acquire electromagnetic fields, which causes a practical obstacle in using random samples, as mentioned in [10, 11].

One of the most prevalent applications of orthogonal polynomials is in the area of interpolation, where those polynomials are used to approximate a function within a certain interval. Recently, the $\ell _1$-minimization-based technique is tailored to interpolate a function that has sparse representation in terms of Legendre and spherical harmonic coefficients, as discussed in [29]. In this case, random samples of Legendre and spherical harmonics are used to construct sensing matrices. Similar to the results in compressed sensing, the RIP plays a pivotal role in showing that a particular number of samples is required to achieve certain error approximation.

Another construction of sensing matrices from some orthogonal polynomials related to the sparse polynomial chaos expansion is investigated in [18]. In order to optimize the sensing matrices, the authors adopt the minimization of coherence sensing matrices from several random samples of Legendre and Hermite polynomials. Using Monte Carlo Markov Chain (MCMC), the authors also derive the coherence of optimal-based random sampling points to employ $\ell _1$-minimization algorithm. Additionally, they also derived the coherence bound for a matrix constructed from those polynomials.

In contrast to all aforementioned results which rely on random samples from certain probability measures, in this work, we derive the coherence bound for deterministic sampling points and utilize properties of Wigner d-functions and their products and their representation in terms of Wigner 3j symbols.

1.2 Summary of contributions

In [8], it was conjectured that the lower-bound on the mutual coherence is tight. In other words, the inner product of columns with equal orders is dominated by the inner product of two columns with zero order and highest degree. In this paper, we prove this conjecture and derive a set of related corollaries.

The main contributions and some of the interesting conclusions of our paper are as follows:

• We show that the product of Wigner D-functions can be written as a linear combination of single Legendre polynomials and Wigner 3j symbols. For equispaced sampling points on the elevation and using the symmetry of Legendre polynomials, we show in Sect. 2.3 that only even degree Legendre polynomials contribute to the analysis, which in turn simplifies the problem formulation.

• In Sects. 4 and 5 , we provide various inequalities and identities for sum of Legendre polynomials and Wigner 3j symbols. We establish monotonic properties of these terms as a function of degree and orders of Wigner D-functions. These results establish a certain ordering between inner products of the columns of the sensing matrix. Particularly we show that, under some conditions, the inner products have a specific order as a function of degrees and orders. As a corollary, we also present that the inner product of columns of equal orders is decreasing with orders and increasing with degree. The result can be used to obtain a lower bound on the mutual coherence. Proofs of main theorem, supporting lemmas, and propositions are given in Sects. 8 and 9

• We numerically verify our results and show that our bound is larger than the Welch bound. Therefore, the desideratum of regular sampling pattern design should be this lower bound rather than the Welch bound. We also extend the sampling pattern design algorithm of [8] to a gradient-descent based algorithm and show that it can achieve the lower bound for spherical harmonics.²

1.3 Notation

The vectors are denoted by bold small-cap letters ${\mathbf {a}},{\mathbf {b}},\dots$. Define ${\mathbb {N}}:=\{1,2,\dots \}$ and ${\mathbb {N}}_0:={\mathbb {N}}\cup \{0\}$. The elevation, azimuth, and polarization angle are denoted by $\theta$, $\phi$, and $\chi$, respectively. The set $\{1, \ldots , m\}$ is denoted by [m]. $\overline{x}$ is the conjugate of x.

2 Definitions and problem formulation

2.1 Wigner D-functions

The rotation group, denoted by $\mathrm {SO}(3)$, consists of all possible rotations of the three-dimensional Euclidean space. Square integrable functions defined on the rotation group is the Hilbert space $L^2(\mathrm {SO}(3))$ with the inner product of functions in this space $f,g \in L^2(\mathrm {SO}(3))$ defined as

$$\begin{aligned} \left\langle f,g\right\rangle :=\int _{\mathrm {SO}(3)} f(\theta ,\phi ,\chi )\overline{g(\theta ,\phi ,\chi )}\mathrm {d}\nu (\theta ,\phi ,\chi ). \end{aligned}$$

Similar to the Fourier basis, which can be seen as the eigenfunctions of Laplace operator on the unit circle, we can also derive eigenfunctions on the rotation group $\mathrm {SO(3)}$. These functions are called Wigner D-functions, sometimes also called generalized spherical harmonics. They are orthonormal basis for $L^2(\mathrm {SO}(3))$. It can be written in terms of Euler angles $\theta \in [0,\pi ]$, and $\phi , \chi \in [0,2\pi )$ as follows

$$\begin{aligned} \mathrm {D}_{l}^{k,n}(\theta ,\phi ,\chi )= N_l e^{-\mathrm {i}k\phi } \mathrm {d}_l^{k,n}(\cos \theta ) e^{-\mathrm {i}n\chi } \end{aligned}$$

(1)

where $N_l=\sqrt{\frac{2l+1}{8\pi ^2}}$ is the normalization factor to guarantee unit $L_2$-norm of Wigner D-functions. The function $\mathrm {d}_{l}^{k,n}(\cos \theta )$ is the Wigner d-function of order $-l\le k,n \le 1$ and degree l defined by

$$\begin{aligned} \mathrm {d}_{l}^{k,n}(\cos \theta ):=\omega \sqrt{\gamma } \sin ^{\xi } \bigg (\frac{\theta }{2}\bigg )\cos ^{\lambda }\bigg (\frac{\theta }{2}\bigg ) P_{\alpha }^{(\xi ,\lambda )}(\cos \theta ) \end{aligned}$$

(2)

where $\gamma =\frac{\alpha !(\alpha + \xi + \lambda )!}{(\alpha +\xi )!(\alpha +\lambda )!}$, $\xi =\left| k-n\right|$, $\lambda =\left| k+n\right|$, $\alpha =l-\big (\frac{\xi +\lambda }{2}\big )$ and

$$\begin{aligned} \omega = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if } n\ge k \\ (-1)^{n-k} &{}\quad \text {if } n<k \end{array}\right. }. \end{aligned}$$

The function $P_{\alpha }^{(\xi ,\lambda )}$ is the Jacobi polynomial.

Wigner D-functions are equal to complex spherical harmonics when the order n is equal to zero, namely

$$\begin{aligned} \mathrm {D}_{l}^{-k,0}(\theta ,\phi ,0) = (-1)^k \sqrt{\frac{1}{2\pi }} \mathrm {Y}_{l}^{k}(\theta ,\phi ), \end{aligned}$$

(3)

where $\mathrm {Y}_{l}^{k}(\theta ,\phi ) :=N^k_l P_l^{k}(\cos \theta ) e^{\mathrm {i}k\phi }$. The term $N^k_l:=\sqrt{\frac{2l+1}{4\pi } \frac{(l-k)!}{(l+k)!}}$ is a normalization factor to ensure the function $\mathrm {Y}_{l}^{k}(\theta ,\phi )$ has unit $L_2$-norm and $P_{l}^k (\cos \theta )$ is the associated Legendre polynomials. Wigner D-functions form an orthonormal basis with respect to the uniform measure on the rotation group, i.e., $\sin \theta \mathrm {d}\theta \mathrm {d}\phi \mathrm {d}\chi$.

$$\begin{aligned} \begin{aligned} \int _{0}^{2\pi }\int _{0}^{2\pi }\int _{0}^{\pi }&\mathrm {D}_{l}^{k,n}(\theta ,\phi ,\chi ) \overline{\mathrm {D}_{l'}^{k',n'}(\theta ,\phi ,\chi )} \sin \theta \mathrm {d}\theta \mathrm {d}\phi \mathrm {d}\chi&=\delta _{ll'} \delta _{kk'} \delta _{nn'}. \end{aligned} \end{aligned}$$

(4)

Similarly, Wigner d-functions are also orthogonal for different degree l and fix order k, n:

$$\begin{aligned} \int _{0}^{\pi } \mathrm {d}_{l}^{k,n}(\cos \theta ) \mathrm {d}_{l'}^{k,n}(\cos \theta ) \sin \theta d\theta = \frac{2}{2l+1}\delta _{l l'}. \end{aligned}$$

(5)

The factor $\frac{2}{2l+1}$ can be used for normalization to get orthonormal pairs of functions.

As discussed earlier, the Wigner d-functions, or weighted Jacobi polynomials, are generalization of hypergeometric polynomials including associated Legendre polynomials, where the relationship between those polynomials can be expressed as

$$\begin{aligned} \mathrm {d}_{l}^{k,0}(\cos \theta ) = \sqrt{\frac{(l-k)!}{(l+k)!}}P_l^k(\cos \theta ). \end{aligned}$$

(6)

The associated Legendre polynomials of degree l and order $-l \le k \le l$ is given as

$$\begin{aligned} P_l^k(\cos \theta ) = (-1)^k (\sin \theta )^{k} \frac{\mathrm {d}^k P_l(\cos \theta ) }{\mathrm {d}(\cos \theta )^k}, \end{aligned}$$

(7)

where $P_l(\cos \theta )$ is Legendre polynomial, and using Rodrigues formula it can be written as

$$\begin{aligned} P_l (\cos \theta ) = \frac{1}{2^l l!}\frac{\mathrm {d}^l}{\mathrm {d}\cos \theta ^l} (\cos ^2\theta -1)^l. \end{aligned}$$

(8)

Similar to Wigner d-functions, Legendre polynomials are also orthonormal. The important properties of associated Legendre polynomials that are necessary in this article are also presented in Sect. 10.2.

2.2 Problem formulation

In many signal processing applications, it is desirable to study properties of matrices constructed from samples of Wigner D-functions. A common example is reconstruction of band-limited functions on $\mathrm {SO}(3)$ from its samples. A function $g \in L^2(\mathrm {SO}(3))$ is band-limited with bandwidth B if it is expressed in terms of Wigner D-functions of degree less than B:

$$\begin{aligned} g(\theta ,\phi ,\chi )=\sum _{l=0}^{B-1}\sum _{k=-l}^{l}\sum _{n=-l}^{l} {\hat{g}}_l^{k,n} \,\mathrm {D}_{l}^{k,n}(\theta ,\phi ,\chi ). \end{aligned}$$

Suppose that we take m samples of this function at points $(\theta _p,\phi _p,\chi _p)$ for $p\in [m]$. The samples are put in the vector $\mathbf{y}$, and the goal is to find the coefficients $\mathbf{g}$. This is a linear inverse problem formulated by $\mathbf{y}=\mathbf{A}\mathbf{g}$, with $\mathbf{A}$ given as

$$\begin{aligned} \mathbf {A}= \begin{pmatrix} \mathrm {D}_{0}^{0,0}(\theta _1,\phi _1,\chi _1)&{}\quad \dots &{}\quad \mathrm {D}_{B-1}^{B-1,B-1}(\theta _1,\phi _1,\chi _1) \\ \mathrm {D}_{0}^{0,0}(\theta _2,\phi _2,\chi _2) &{}\quad \dots &{}\quad \mathrm {D}_{B-1}^{B-1,B-1}(\theta _2,\phi _2,\chi _2) \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ \mathrm {D}_{0}^{0,0}(\theta _m,\phi _m,\chi _m) &{}\quad \dots &{}\quad \mathrm {D}_{B-1}^{B-1,B-1}(\theta _m,\phi _m,\chi _m) \end{pmatrix}. \end{aligned}$$

(9)

For index column $q \in [N]$, we denotes the degree and orders of the respective Wigner D-function by l(q), k(q) and n(q).³ The column dimension of this matrix is given by $N =\frac{B(2B-1)(2B+1)}{3}$. Using these functions, the elements of this matrix are given by

$$\begin{aligned} \mathbf{A}=[{A}_{p,q}]_{p\in [m],q\in [N]}:\quad {A}_{p,q}=\mathrm {D}_{l{(q)}}^{k{(q)},n{(q)}}(\theta _p,\phi _p,\chi _p). \end{aligned}$$

(10)

In compressed sensing, the sensing matrix $\mathbf{A}$ with lower mutual coherence are more desirable for signal reconstruction [15]. The mutual coherence, denoted by $\mu (\mathbf{A})$ is expressed as

$$\begin{aligned} \begin{aligned}&\underset{ 1 \le r < q \le N}{\text {max}} \,\,\left| \sum _{p=1}^{m}\frac{ \mathrm {D}_{l{(q)}}^{k{(q)},n{(q)}}(\theta _p,\phi _p,\chi _p) \overline{\mathrm {D}_{l{(r)}}^{k{(r)},n{(r)}}(\theta _p,\phi _p,\chi _p)}}{\left\| \mathrm {D}_{l{(q)}}^{k{(q)},n{(q)}}(\varvec{\theta },\varvec{\phi },\varvec{\chi })\right\| _2 \left\| \mathrm {D}_{l{(r)}}^{k{(r)},n{(r)}}(\varvec{\theta },\varvec{\phi },\varvec{\chi })\right\| _2}\right| , \end{aligned} \end{aligned}$$

(11)

where we adopt the following convention

$$\begin{aligned}\mathrm {D}_{l}^{k,n}(\varvec{\theta },\varvec{\phi },\varvec{\chi }):=\begin{pmatrix} \mathrm {D}_{l}^{k,n}(\theta _1,\phi _1,\chi _1)\\ \vdots \\ \mathrm {D}_{l}^{k,n}(\theta _m,\phi _m,\chi _m) \end{pmatrix}. \end{aligned}$$

For the rest of the paper, we focus mainly on the inner product between the samples. It can be numerically verified that the $\ell _2$-norm of columns do not affect the coherence value. We will comment later on how these norms scale.

Although the closed-form derivation of mutual coherence is in general difficult, the authors in [8] observed empirically that the mutual coherence of sensing matrices with equispaced sampling points on the elevation angle is indeed tightly bounded by a single term under certain assumptions. This is because the inner products of Wigner D-functions are ordered in a regular way as a function of their orders and degrees. In this paper, we provide theoretical supports for these observations. In other words, we provide simple analysis of mutual coherence for specific sampling patterns. Central to our analysis is a set of combinatorial identities about the sum and product of Wigner D-functions. We will focus on the equispaced sample on $\theta _p$ for $p\in [m]$, which are chosen such that

$$\begin{aligned} \cos \theta _{p} = \frac{2p-m-1}{m-1}. \end{aligned}$$

(12)

This means that $-1=\cos \theta _{1}<\cos \theta _2<\cdots< \cos \theta _{m-2}< \cos \theta _{m-1} < \cos \theta _{m}=1$. There are multiple reasons for using this sampling pattern. First of all, this sampling pattern has been shown to be beneficial in spherical near-field antenna measurement [7, 10] where the robotic probe can acquire the electromagnetic field samples and move in the same distance. Second of all, this sampling pattern induces orthogonal columns in the sensing matrix between even and odd degree polynomials as discussed in [8, Theorem 5]. Interestingly, fixing the sampling patterns on the elevation imposes a lower bound on the mutual coherence, which is tight in many cases. In this paper, we study the mutual coherence for this elevation sampling and arbitrary sampling patterns on $\phi$ and $\chi$.

2.3 Product of Wigner D-functions

In the expression for mutual coherence, product of Wigner D-functions appears constantly. This product appears also in the study of angular momentum in quantum mechanics and can be written as linear combination of a single Wigner D-functions with coefficients, called Wigner 3j symbols [14, 30, 31]. Using this representation, the discrete inner product of Wigner D-functions can be simplified as follows.

Proposition 1

[8]

Let $\mathrm {D}_{l}^{k,n}(\theta ,\phi ,\chi )$ be the Wigner D-function with degree l and orders k, n. Then we have:

$$\begin{aligned}&\sum _{p=1}^m\overline{\mathrm {D}_{l_1}^{k_1,n_1}(\theta _p,\phi _p,\chi _p)} \mathrm {D}_{l_2}^{k_2,n_2}(\theta _p,\phi _p,\chi _p) \nonumber \\&\quad = C_{k_2,n_2}\sum _{\begin{array}{c} {{\hat{l}}}=|l_2-l_1| \end{array}}^{l_1 + l_2} \sqrt{\frac{(2l_1 + 1)(2l_2 +1)(2{\hat{l}} + 1)}{8 \pi ^2}} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -n_1 &{}\quad n_2 &{}\quad -{\hat{n}} \end{pmatrix}\nonumber \\&\qquad \times \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -k_1 &{}\quad k_2 &{}\quad -{\hat{k}} \end{pmatrix} \sum _{p=1}^m \mathrm {D}_{{\hat{l}}}^{{\hat{k}},{\hat{n}}}(\theta _p,\phi _p,\chi _p) , \end{aligned}$$

(13)

where ${\hat{k}} = k_2-k_1$, ${\hat{n}} = n_2 - n_1$ with the phase factor $C_{k_2,n_2} = (-1)^{k_2 + n_2}$.

The parameters of Wigner 3j symbols are non-zero only under certain conditions known as the selection rules. The selection rules state that Wigner 3j symbols $\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {l}_3 \\ k_1 &{}\quad k_3 &{}\quad k_3 \end{pmatrix} \in {\mathbb {R}}$ are non-zero if only if:

• The absolute value of $k_i$ does not exceed $l_i$, i.e., $-l_i \le k_i \le l_i$ for $i=1,2,3$

• The summation of all $k_i$ should be zero: $k_1 + k_2 +k_3 = 0$.

• Triangle inequality holds for $l_i$’s: $\left| l_1 - l_2\right| \le l_3 \le l_1 + l_2$.

• The sum of all $l_i$’s should be an integer $l_1+l_2+l_3 \in \mathbb {N}$.

• If $k_1 = k_2 = k_3 = 0$, $l_1+l_2+l_3 \in \mathbb {N}$ should be an even integer.

There are other identities that will be useful for our derivations. For degrees $l_1,l_2$, orders $k_1,k_2,n_1,n_2$, and ${\hat{k}} = k_1 + k_2$, ${\hat{n}} = n_1 + n_2$, we obtain the following identities [14, 30, 31].

$$\begin{aligned} \begin{aligned}&\sum _{{\hat{l}}=\left| l_1-l_2\right| }^{l_1+l_2} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ k_1 &{}\quad k_2 &{}\quad -{\hat{k}} \end{pmatrix}^2 = 1, \,\, \\&\sum _{{\hat{l}}=\left| l_1-l_2\right| }^{l_1+l_2} (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ n_1 &{}\quad n_2 &{}\quad {\hat{n}} \end{pmatrix}\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ k_1 &{}\quad k_2 &{}\quad -{\hat{k}} \end{pmatrix} = 0 ,&\text {for} \,\, k_1 \ne n_1 \text {and} k_2 \ne n_2. \end{aligned} \end{aligned}$$

(14)

Note that, from the selection rules, if $l_1 + l_2 + {\hat{l}}$ is an odd integer, then $\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}$ is zero. Further properties and the exact expression of the Wigner 3j symbol will be included in Sect. 10.4.

It is trivial to derive the product of same orders Wigner d-function, i.e., $k_1 = k_2 = k$ and $n_1 = n_2 = n$, as follows

$$\begin{aligned} \begin{aligned}&\left| \sum _{p=1}^m \mathrm {d}_{l_1}^{k ,n }(\cos \theta _p) \mathrm {d}_{l_2}^{k,n }(\cos \theta _p)\right| \\&\quad = \left| \sum _{\begin{array}{c} {{\hat{l}}}=|l_2-l_1| \end{array}}^{l_1 + l_2} (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -n &{}\quad n &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -k &{}\quad k &{}\quad 0 \end{pmatrix} \sum _{p=1}^mP_{{\hat{l}}}(\cos \theta _p)\right| \end{aligned}\nonumber \\ \end{aligned}$$

(15)

An interesting conclusion of the above identities is that the sampling pattern affects the inner product through the sum of individual functions, for instance Legendre polynomials.

3 Main results

The starting point of bounding the coherence is the following trivial inequality, which holds in full generality:

$$\begin{aligned} \mu (\mathbf{A}) \ge \max _{\begin{array}{c} {l_1\ne l_2}\\ {|k|,|n|\le \min {(l_1,l_2)}} \end{array}} \left| \frac{ \sum _{p=1}^{m} \mathrm {d}_{l_1}^{k,n}(\cos \theta _p)\mathrm {d}_{l_2}^{k,n}(\cos \theta _p) }{ \left\| \mathrm {d}_{l_1}^{k,n}(\cos \varvec{\theta })\right\| _2 \left\| \mathrm {d}_{l_2}^{k,n}(\cos \varvec{\theta }{)}\right\| _2 } \right| . \end{aligned}$$

(16)

This is obtained by choosing the column with equal orders of k and n, and using Definition 1. In other words, for any sampling pattern, regardless of the choice of $\phi _p$ and $\chi _p$, the mutual coherence is lower bounded by merely choosing $\theta _p$. This indicates the sensitivity of mutual coherence to the sampling pattern on the elevation. The following theorem shows that the maximum inner product in above expression has a simple solution for the sampling pattern (12) if m is moderately large.

Theorem 1

Consider Wigner d-functions of degree $0< l_1 < l_2 \le B-1$ and orders $-\text {min}(l_1 ,l_2)\le k,n \le \text {min}(l_1,l_2)$, which are sampled according to (12) with $m \ge \frac{(B + 2)^2}{10} + 1$. We have

$$\begin{aligned} \begin{aligned} \max _{\begin{array}{c} {l_1\ne l_2}\\ {|k|,|n|\le \min {(l_1,l_2)}} \end{array}}&\left| \sum _{p=1}^{m} \mathrm {d}_{l_1}^{k,n}(\cos \theta _p)\mathrm {d}_{l_2}^{k,n}(\cos \theta _p)\right| = \left| \sum _{p=1}^{m} {P}_{B-1}(\cos \theta _p) {P}_{B-3}(\cos \theta _p)\right| , \end{aligned}\nonumber \\ \end{aligned}$$

(17)

where ${P}_l (\cos {\varvec{\theta }})$ is the Legendre polynomial of degree l with

$$\begin{aligned} P_{l} (\cos \varvec{\theta }):=\left( {P}_{l}(\cos \theta _1),\dots ,{P}_{l}(\cos \theta _m)\right) ^T. \end{aligned}$$

Intuitively, this theorem states that if one considers equispaced samples on the elevation, the maximum inner product occurs at the zero-order Wigner d-functions, which are Legendre polynomials. Additionally, we can obtain similar results for maximum discrete inner product of associated Legendre polynomials, since for $k=0$ or $n=0$, the Wigner d-functions are the associated Legendre polynomials. The result is given in the following corollary.

Corollary 1

Let $\theta _p$’s for $p \in [m]$ be chosen as in (12). For $m \ge \frac{(B + 2)^2}{10} + 1$, we have

$$\begin{aligned} \begin{aligned} \max _{\begin{array}{c} {l_1\ne l_2}\\ {|k|\le \min {(l_1,l_2)}} \end{array}}\,\,&\left| \sum _{p=1}^{m} C_{l_1}^kC_{l_2}^kP^k_{l_1}(\cos \theta _p)P^k_{l_2}(\cos \theta _p)\right| =&\left| \sum _{p=1}^{m} P_{B-1}(\cos \theta _p)P_{B-3}(\cos \theta _p)\right| , \end{aligned}\nonumber \\ \end{aligned}$$

(18)

where $C^k_{l} = \sqrt{\frac{(l-k)!}{(l+k)!}}$ is the normalization factor.

Corollary 1 implies that the maximum product of two associated Legendre polynomials for different degrees and same orders is also attained at degrees $B-1$ and $B-3$ and order $k=0$.

Remark 1

A byproduct of Theorem 1 is that for a fixed number of measurement numbers m, the inner product of Wigner d-functions with degree less that $\sqrt{10 m}$ are ordered. This surprising behavior in presented in numerical experiments.

The proof of the main result follows from a sequence of inequalities and identities. In the next sections, we provide some of them that are of independent interest. Interestingly, the well-ordered behaviour of the inner products of Wigner d-functions is linked to orders in the summand of (15). The proof leverages mostly classical inequalities and identities, e.g., Abel partial summation, and the orders between Wigner d-functions. All the proofs for the following sections are given in Sect. 9.

4 Finite sum of Legendre polynomials

The starting point of the proof is to use (15) for the product of Wigner d-functions. The proof strategy is based on establishing inequalities for each term in the sum (15), and then using them to bound the final sum. In this section, we provide a set of results for sum of Legendre polynomials. The following lemma provides an identity for the sum of equispaced samples of Legendre polynomials.

Lemma 1

For equispaced samples given in (12), the sum of sampled Legendre polynomials for even degrees $l > 0$ is given by

$$\begin{aligned} \sum _{p=1}^{m} P_{l}(\cos \theta _p) =1+\frac{l(l+1)}{6(m-1)}+ R_l(m), \end{aligned}$$

where $\frac{l(l+1)}{6(m-1)} + R_l(m)$ is equal to $\sum _{\begin{array}{c} k = 2 \\ k,\text {even} \end{array}}^l \frac{(-1)^{\frac{k}{2} + 1}S_l^k}{(m-1)^{k-1}}$ and $S_l^k = \frac{\zeta (k) (l+k-1)! 4 }{(k-1)! (l-k+1)! (2\pi )^k}$ with $\zeta (k)$ is the zeta function. For odd degrees l, the sum is equal to zero.

Lemma 1 shows that we can simplify the summation of equispaced samples Legendre polynomials in terms of the number of samples m, the degree of polynomials l, and the residual $R_l(m)$.

Remark 2

If $l=0$, then the sum of equispaced samples Legendre polynomials is equal to m, since $P_0 (\cos \theta ) = 1$. In addition, for $l=2$, the summation is equal to $1 + \frac{1}{m-1}$ and we do not have any residual. If we take a number of samples larger than the degree l, it is obvious that the summation converges to 1.

The residual $R_l(m)$ is important in the summation in Lemma 1. We provide upper and lower bounds on the residual $R_l(m)$. The next proposition provides a bound on this summation.

Proposition 2

For $m \ge \frac{(l+1)^2}{10} + 1$ with even degree $l \ge 4$, the residual $R_{l}(m)$ is bounded as $-0.463< R_l(m) < 0$.

The previous proposition shows that the residual, conditioned on $m \ge \frac{(l+1)^2}{10} + 1$, is inside the interval, and most importantly is always negative. We present the numerical evaluation of this bound in Sect. 6. Using this property, it can be shown that not only the summation $\sum _{p=1}^{m} P_{l}(\cos \theta _p)$ is non-negative, but also it is monotonically increasing for an increasing even degree l.

Lemma 2

For $m \ge \frac{(B + 2)^2}{10} + 1$, the sum of equispaced samples of Legendre polynomials for even degrees $0 \le l \le B-1$ is non-negative, i.e., $\sum _{p=1}^{m} P_{l}(\cos \theta _p) \ge 0$. Moreover, for an increasing sequence of even degrees l, i.e., $2< 4< 6< \cdots < B-1$, we have $\sum _{p=1}^{m} P_{2}(\cos \theta _p)< \sum _{p=1}^{m} P_{4}(\cos \theta _p)< \sum _{p=1}^{m} P_{6}(\cos \theta _p)< \cdots < \sum _{p=1}^{m} P_{B-1}(\cos \theta _p).$

Lemma 1, Proposition 2, and Lemma 2 characterize the order of the sum of equispaced samples of Legendre polynomials. These properties are useful later to prove the main result in this paper. In the next section, we show a similar ordering for other terms of expression in (15).

5 Inequalities for Wigner 3j symbols

To prove the main theorem, we establish that there is a similar order between Wigner 3j symbols. Some of these properties of Wigner 3j symbols are given in Sects. 2 and 10.4. In what follows, we will have some combinatorial identities and inequalities related to Wigner 3j symbols. Despite ample investigation of authors, it is not clear whether these results bear interesting implications for other areas particularly angular momentum analysis in quantum physics. For compressed sensing, however, these are quite interesting as they show that the sensing matrix from samples Wigner D-functions possesses a lot of structures and symmetries. We start with the following lemma.

Lemma 3

For all degrees $0 \le l_1 < l_2 \le B-1$ and $l_3$, the following inequalities hold:

$$\begin{aligned} \begin{aligned} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2&\ge \begin{pmatrix} l_1+1 &{}\quad l_2+1 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2,\\ \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2&\ge \begin{pmatrix} l_1+2 &{}\quad l_2 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2. \end{aligned} \end{aligned}$$

(19)

By reducing the indices one at a time, this result shows that the maximum of Wigner 3j symbols for zero order is achieved at zero degree. From (14), it follows that the maximum is equal to 1. The summation of Wigner 3j symbols for $k_1 = k_2$, which is important for our proof of the main result, can be decomposed into the summation of terms with odd and even degrees. The following lemma provides the closed form solution for this summation.

Lemma 4

Suppose that $l_1 \ne l_2 \in \mathbb {N}$ and $\left| l_1-l_2\right| \le {\hat{l}} \le l_1 + l_2$. Then for $-\text {min}(l_1,l_2) \le k\ne n \le \text {min}(l_1,l_2)$, we have

$$\begin{aligned} \begin{aligned}&\sum _{{\hat{l}},\mathrm {even}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -k &{}\quad k &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -n &{}\quad n &{}\quad 0 \end{pmatrix} \\&\quad = \sum _{{\hat{l}},\mathrm {odd}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -k &{}\quad k &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad \quad {\hat{l}}\\ -n &{}\quad n &{}\quad 0 \end{pmatrix}&= 0. \end{aligned} \end{aligned}$$

Furthermore, for $k=n=\tau$ and $1 \le \left| \tau \right| \le \text {min}(l_1,l_2)$ we have

$$\begin{aligned} \begin{aligned} \sum _{{\hat{l}},\mathrm {even}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{} \quad {\hat{l}}\\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2&= \sum _{{\hat{l}},\mathrm {odd}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2 = \frac{1}{2} \end{aligned} \end{aligned}$$

Remark 3

For $\tau = 0$, , i.e., for $\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$, we can obtain a similar identity to the last identity in Lemma 4. In this case, the selection rules in Sect. 2 imply that the sum $l_1 + l_2 + {\hat{l}}$ should be an even integer, which means that for even ${\hat{l}}$ and odd $l_1 + l_2$, the Wigner 3j symbols value is zero. When $l_1+l_2$ is even, from the orthogonal property of Wigner 3j symbols as in (14), we have

$$\begin{aligned} {\sum _{{\hat{l}},\mathrm {even}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2 = 1, \quad \text {for} \quad l_1 + l_2 \quad \text {is even}.} \end{aligned}$$

The last result of this section is related to the product of Wigner 3j symbols and ${\hat{l}}({\hat{l}} + 1)$, where $\left| l_1 - l_2\right| \le {\hat{l}} \le l_1 + l_2$ and $l_2 = l_1 + 2$. As discussed in Lemma 1, the sum of equispaced samples Legendre polynomials can be expressed as $\sum _{p=1}^m P_l(\cos \theta _p) = 1 + \frac{l(l+1)}{6(m-1)} + R_l(m)$, where $R_l(m)$ is the residual. The following lemma gives an expression of the inner product between Wigner 3j symbols and ${\hat{l}}({\hat{l}}+1)$.

Lemma 5

For Wigner 3j symbols $\begin{pmatrix} l_1 &{}\quad l_1 + 2 &{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}$ with the degrees satisfying $l_2=l_1+2$ and $2 \le {\hat{l}} \le 2l_1 + 2$, the following equality holds:

$$\begin{aligned} \begin{aligned}&\sum \limits _{\begin{array}{c} {\hat{l}}= 2 \\ {\hat{l}},\mathrm {even} \end{array}}^{2l_1 + 2} (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_1 + 2 &{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2({\hat{l}}^2 + {\hat{l}}) = 2 + 2(l_1+2)(l_1 +1). \end{aligned} \end{aligned}$$

Since we consider degree $0 \le l_1 < l_2 \le B-1$ and order $k=n=0$, the previous lemma has a direct implication for $l_1 = B-3$ and $l_2 =B-1$, as given in the following corollary.

Corollary 2

Suppose $l_1 = B-3$ and $l_2 = B-1$, then we have

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} {\hat{l}}=2 \\ {\hat{l}},\mathrm {even} \end{array}}^{2B -4} (2{\hat{l}} + 1) \begin{pmatrix} B-3 &{}\quad B-1 &{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2({\hat{l}}^2 + {\hat{l}}) = 2 + 2(B-1)(B-2). \end{aligned} \end{aligned}$$

This corollary is important to determine the product of Wigner 3j symbols and the sum of equispaced samples of Legendre polynomials. Since the latter can be expressed by ${\hat{l}}({\hat{l}} + 1)$, as shown in Lemma 1 , we can directly apply Lemma 5 to estimate the product.

6 Experimental results

In what follows, we conduct a series of experiments to verify some of the results in the paper, as well as applications in compressed sensing. First, we would like to investigate how tight the main result of this paper is. In other words, how pessimistic the condition on the number of measurements m is for the lower bound to hold. Second, we investigate how tight the lower-bound on the mutual coherence is. From the first part, we can gain intuitions on the choice of number of measurements. From the second part, we can see if the lower bound on the mutual coherence for a chosen m is attainable or not.

6.1 Numerical verification of theoretical results

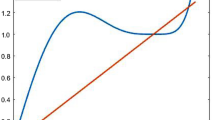
In Lemma 1, we can express the sum of equispaced samples Legendre polynomials as $\sum _{p=1}^{m} P_{l}(\cos \theta _p) =1+\frac{l(l+1)}{6(m-1)}+ R_l(m)$, where $R_l(m)$ is the residual with interval $-0.463< R_l(m) < 0$ by assuming $m \ge \frac{(l + 1)^2}{10} + 1$, as in Proposition 2. One might ask if this condition can be relaxed while keeping the residual error controlled. The numerical evaluation of this proposition is presented in Fig. 1. It can be seen that by considering $m = \frac{(l + 1)^2}{10} + 1$, represented with the black line, the residual is restricted within the interval by the blue and red colors, respectively. In other words, the obtained constants are indeed tight in Proposition 2 and the bound on m cannot be potentially improved.

Fig. 1

Residual error of sum of equispaced samples Legendre polynomials from $1+\frac{l(l+1)}{6(m+1)}$

Next, we numerically evaluate Theorem 1. Even though the bound on m can characterize tightly the residual error, it is interesting to see if the bound is tight for Theorem  1. For applications, this result is more relevant, as it indicates if a deviation from the inequality and choosing smaller m can invalidate the lower bound. In Fig. 2, we show for which pairs of (m, B), the identity of Theorem 1 holds using the color red. We have furthermore included a black line indicating the number of samples as in Theorem 1 for different B. It can be seen for small B, the condition is tight. However, it seems that it can be improved for larger values of B. It is in general difficult to build an intuition on where the identity of Theorem 1 holds, although the condition of the theorem definitely provides a rule of thumb. To emphasize, it can be seen that our bound is pessimistic, which means that we can find a looser condition on m for which the result of Theorem 1 holds. The relation still seems to be quadratic in B.

Finally, in Fig. 2, the numerical experiments are performed by considering the normalization with respect to the $\ell _2$-norm. Thereby, we can numerically verify that the normalization does not affect the inequality in Theorem 1.

Fig. 2

Numerical verification of Theorem 1

6.2 Comparison with Welch bound and designing sampling patterns

Our theoretical result provides a lower bound on the mutual coherence for equispaced samples on the elevation angle. Specifically, we have $\cos \theta _p = \frac{2p - m - 1}{m-1}$ for $p \in [m]$. It is interesting to see if the bound improves on previously existing bounds, like Welch bound, and if the bound can be somehow achieved. Note that Welch bound holds for any sensing matrix including those constructed from samples of spherical harmonics and Wigner D-functions. Our bound can be only useful if it improves on Welch bound.

In order to design sensing matrices from spherical harmonics and Wigner D-function, we obtain points on azimuth and polarization angles $\phi ,\chi \in [0, 2\pi )$ by solving the optimization problem below:

$$\begin{aligned} \begin{aligned}&\underset{\varvec{\phi }, \varvec{\chi }}{\text {minimize}}&\underset{ 1 \le r < q \le N}{\text {max}} \left| f_{q,r}(\varvec{\theta },\varvec{\phi },\varvec{\chi })\right| \\&\text {subject to}&\phi _p,\chi _p \in [0,2\pi ] \quad \text {for} \quad p \in [m] \end{aligned} \end{aligned}$$

where $f_{q,r}(\varvec{\theta },\varvec{\phi },\varvec{\chi })$ is given as

$$\begin{aligned} \frac{\sum _{p=1}^{m} \mathrm {D}_{l{(q)}}^{k{(q)},n{(q)}}(\theta _p,\phi _p,\chi _p) \overline{\mathrm {D}_{l{(r)}}^{k{(r)},n{(r)}}(\theta _p,\phi _p,\chi _p)}}{\left\| \mathrm {D}_{l{(q)}}^{k{(q)},n{(q)}}(\varvec{\theta },\varvec{\phi },\varvec{\chi })\right\| _2 \left\| \mathrm {D}_{l{(r)}}^{k{(r)},n{(r)}}(\varvec{\theta },\varvec{\phi },\varvec{\chi })\right\| _2}. \end{aligned}$$

For spherical harmonics, a similar optimization problem is used using the relation in (3) without constraint on the polarization angle $\chi$ and order n.

This optimization problem is a challenging min-max problem with non-smooth objective function and generally non-convex. In [8], we have used a search-based method for optimization, which turns out to be difficult to tune and more time-consuming. We introduce a relaxation of the above problem and use gradient-descent based algorithms for optimizing it. The derivatives of spherical harmonics and Wigner D-functions are given in Sect. 10.1.1.

Using a property of the $\ell _p$-norm, we can write the objective function as

$$\begin{aligned} \underset{\varvec{\phi }, \varvec{\chi }}{\text {min}}\,\, \underset{p \rightarrow \infty }{\lim } \left( \underset{1 \le r < q \le N}{\sum } \left| f_{q,r}(\varvec{\theta },\varvec{\phi },\varvec{\chi })\right| ^{p}\right) ^{1/p}. \end{aligned}$$

One can choose large enough p and calculate the gradient. Therefore, we can relax the optimization problem from min-max to minimization of the $\ell _p$-norm with large enough p. We can then use gradient descent algorithms to solve this problem, as given in Algorithm 1.

Fig. 3

Coherence of Wigner D-functions sensing matrix ($B = 8$)

Figure 3 shows the coherence of the sensing matrix from Wigner D-functions using sampling points generated from several stochastic gradient algorithms. Although there are no sampling points that reach the lower bound in Theorem 1, it can be seen that Adam algorithm [22] yields the best sampling points. In this work, we also compare with several well-known stochastic gradient descent, as given in [13, 22, 35]. The bandwidth of Wigner D-functions is chosen as ${B=8}$, which means that the column dimension is ${N = 680}$.

Algorithm 1 can be tailored for spherical harmonics by only considering the azimuth parameter $\varvec{\phi }$ and using relation between Wigner D-functions and spherical harmonics in (3). It can be seen that most of the gradient descent based algorithms converge to the lower bound for spherical harmonics, as shown in Fig. 4. Therefore, we can provide sampling points on the sphere with mutual coherence that can achieve the the lower bound in Theorem 1. In this case, the spherical harmonics are generated with the bandwidth ${B=26}$ or equivalently we have the column dimension ${N = 676}$. In other words, our lower bound is strictly better than Welch bound for spherical harmonics and achievable by a sampling pattern.

Fig. 4

Coherence of spherical harmonics sensing matrix ($B = 26)$

7 Conclusions and future works

We have established a coherence bound of sensing matrices for Wigner D-functions on regular grids. This result also holds for spherical harmonics, which is a special case of Wigner D-functions. Estimating coherence involves non-trivial and complicated product of two Wigner D-functions for all combination of degrees and orders, yielding an obstacle to derive a simple and compact formulation of the coherence bound. Using the tools from the area of angular momentum analysis in quantum mechanics, the inner products in the coherence expression can be represented as a linear combination of single Wigner D-functions and angular momentum coefficients, so called Wigner 3j symbols. In this paper, we derive some interesting properties of these coefficients and finite summation of Legendre polynomials to obtain the coherence bound. We have also provided numerical experiments in order to verify the tightness of this bound. For practical applications, it is also necessary to provide sampling points on the sphere and the rotation group that can achieve the coherence bound. We have shown that, for spherical harmonics, one can generate points to achieve this bound by using a class of gradient descent algorithms. Convergence analysis of these algorithms and construction of deterministic sampling points to achieve this bound will be relegated to future works.

8 Proof of the main theorem

Proof

In order to prove the main theorem, it is enough to show that for the degrees $0 \le l_1 < l_2 \le B-1$ and the orders $-\text {min}(l_1,l_2) \le k,n \le \text {min}(l_1,l_2)$, the following inequality holds

$$\begin{aligned} \left| \sum _{p=1}^{m} {P}_{B-1}(\cos \theta _p) {P}_{B-3}(\cos \theta _p)\right| \ge \left| \sum _{p=1}^{m} \mathrm {d}_{l_1}^{k,n}(\cos \theta _p)\mathrm {d}_{l_2}^{k,n}(\cos \theta _p)\right| . \end{aligned}$$

(20)

We can expand the product of Wigner d-functions in the right hand side as

$$\begin{aligned} \sum _{\begin{array}{c} {{\hat{l}}}=|l_2-l_1|\\ {\hat{l}},\text {even} \end{array}}^{l_1+l_2} (2{\hat{l}} + 1) \begin{pmatrix} l_1&{}\quad l_2&{}\quad {\hat{l}} \\ -n &{}\quad n &{}\quad 0 \end{pmatrix}\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -k &{}\quad k &{}\quad 0 \end{pmatrix}\sum _{p=1}^m P_{{\hat{l}}} (\cos \theta _p). \end{aligned}$$

The sum includes only terms with even ${\hat{l}}$. This is because Legendre polynomials are odd functions for odd values of ${\hat{l}}$, and therefore the internal sum, which is over values symmetric around zero, will be zero. Additionally, the product of Legendre polynomials in the left hand side can be written as

$$\begin{aligned} \sum _{\begin{array}{c} {{\hat{l}}}=2\\ {\hat{l}},\text {even} \end{array}}^{2B-4} (2{\hat{l}} + 1) \begin{pmatrix} B-3&{}\quad B-1&{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2\sum _{p=1}^m P_{{\hat{l}}} (\cos \theta _p). \end{aligned}$$

The proof is divided into two parts. We consider first order $k = n = 0$ and then the rest of orders k, n.

Let’s consider the first case, for zero order $k = n = 0$.

From (6), we know that $\mathrm {d}_{l}^{0,0}(\cos \theta ) = P_l(\cos \theta )$. Therefore, it is enough to prove that the maximum product of two Legendre polynomials is attained at $l_1=B-3$ and $l_2 = B-1$, i.e., ${\max }_{l_1 \ne l_2}\left| \sum _{p=1}^{m} P_{l_1}(\cos \theta _p)P_{l_2}(\cos \theta _p)\right| =\left| \sum _{p=1}^{m} P_{B-1}(\cos \theta _p)P_{B-3}(\cos \theta _p)\right| .$ We show that for an even $l_1+l_2$, if $(l_1,l_2)$ is increased to either $(l_1+1,l_2+1)$ or $(l_1+2,l_2)$, the sum of the product of two Legendre polynomials increases. It is enough to consider these two situations since from any pair $(l_1,l_2)$, one can use a sequence of inequalities to arrive at $(B-3,B-1)$. For odd $l_1+l_2$, the inner product is zero, and therefore, we can only focus on even $l_1+l_2$.

We use the product in (15) for $k=n=0$ to get the representation of $\sum _{p=1}^mP_{l_1}(\cos \theta _p) P_{l_2}(\cos \theta _p)$ as

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} {{\hat{l}}}=|l_2-l_1|\\ {\hat{l}}, \text {even} \end{array}}^{l_1 + l_2} (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2 \sum _{p=1}^{m} P_{{\hat{l}}} (\cos \theta _p)=\sum _{\begin{array}{c} {\hat{l}}=|l_2-l_1|\\ {{\hat{l}}}, \text {even} \end{array}}^{l_2+l_1} a_{{\hat{l}}}c_{{\hat{l}}}, \end{aligned} \end{aligned}$$

(21)

where $c_{{\hat{l}}}=\sum _{p=1}^{m}P_{{\hat{l}}} (\cos \theta _p)$. From Lemma 2, $c_{{\hat{l}}}$ is non-negative and increasing for even values of ${{\hat{l}}} \ge 2$. The corresponding Wigner 3j symbols for $(l_1,l_2,{{\hat{l}}})$ is denoted by $a_{{\hat{l}}}=(2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$. Suppose we have $b_{{\hat{l}}}=(2{\hat{l}} + 1) \begin{pmatrix} l_1+1 &{}\quad l_2+1 &{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$ for $(l_1 + 1,l_2+1)$ or $b_{{\hat{l}}}=(2{\hat{l}} + 1) \begin{pmatrix} l_1+2 &{}\quad l_2 &{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$ for $(l_1 + 2,l_2)$. From Lemma 3 we have $a_{{{\hat{l}}}}\ge b_{{{\hat{l}}}}$ for both cases and additionally $\sum _{{{\hat{l}}}}a_{{\hat{l}}} =1$ and $\sum _{{{\hat{l}}}}b_{{\hat{l}}}=1$, as pointed out in (14). By using Abel’s partial summation formula as stated in (53), we have

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} {{\hat{l}}}=|l_2-l_1|\\ {{\hat{l}}}, \text {even} \end{array}}^{l_1+l_2} a_{{\hat{l}}} c_{{\hat{l}}}&=\sum _{\begin{array}{c} {{\hat{l}}}=|l_2-l_1|\\ {{\hat{l}}}, \text {even} \end{array}}^{l_2+l_1} A_{{{\hat{l}}}}(c_{{{\hat{l}}}} - c_{{{\hat{l}}}+2})+c_{l_1 + l_2 + 2}, \\ \sum _{\begin{array}{c} {{\hat{l}}}=|l_2-l_1|\\ {{\hat{l}}}, \text {even} \end{array}}^{l_1+l_2+2} b_{{\hat{l}}} c_{{\hat{l}}}&=\sum _{\begin{array}{c} {{\hat{l}}}=|l_2-l_1|\\ {{\hat{l}}}, \text {even} \end{array}}^{l_2+l_1} B_{{{\hat{l}}}}(c_{{{\hat{l}}}} - c_{{{\hat{l}}}+2})+c_{l_1 + l_2 + 2}, \end{aligned} \end{aligned}$$

(22)

where $A_{{\hat{l}}} = \sum _{j, \text {even} =\left| l_1 -l_2\right| }^{{\hat{l}}} a_{j}$ and $B_{{{\hat{l}}}}$ are defined accordingly for $b_{{{\hat{l}}}}$. Since $A_{{{\hat{l}}}}\ge B_{{{\hat{l}}}}$ and $c_{{{\hat{l}}}}$ is increasing, it is clear that $\sum _{{{\hat{l}}}} a_{{\hat{l}}} c_{{\hat{l}}}\le \sum _{{{\hat{l}}}} b_{{\hat{l}}} c_{{\hat{l}}}$, which establishes desired result for $k=n=0$ by increasing the degrees until they reach $l_1 = B-3$ and $l_2 = B-1$.

Next, for $k \ne n$ and $k = n \ne 0$, we want to show that the inequality holds as well. First, define $\alpha _{{\hat{l}}}$ equal to Wigner 3j symbols $\alpha _{{\hat{l}}} := (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -n &{}\quad n &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -k &{}\quad k &{}\quad 0 \end{pmatrix}$ and $c_{{\hat{l}}} = \sum _{p=1}^m P_{{\hat{l}}}(\cos \theta _p) \ge 0$ from Lemma 2. From Lemma 4, we have $\sum _{\begin{array}{c} {\hat{l}}=|l_2-l_1|\\ {{\hat{l}}},\text {even} \end{array}}^{l_2+l_1}\alpha _{{{\hat{l}}}}=0$ for $-\text {min}\left( l_1,l_2\right) \le k \ne n \le \text {min}\left( l_1,l_2\right)$. We can define an independent variable $\kappa = \frac{c_{\left| l_1 -l_2\right| } + c_{l_1 + l_2}}{2}$. An upper bound of the product $\left| \sum _{p=1}^m \mathrm {d}_{l_1}^{k,n}(\cos \theta _p) \mathrm {d}_{l_2}^{k,n}(\cos \theta _p)\right|$ is given by

$$\begin{aligned} \begin{aligned} \left| \sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| \\ {\hat{l}},\text {even} \end{array}}^{l_1 + l_2} \left( c_{{\hat{l}}} - \kappa \right) \alpha _{{\hat{l}}}\right|&\le \frac{c_{\left| l_1 + l_2\right| } - c_{\left| l_1 -l_2\right| }}{2} \sum _{\begin{array}{c} {\hat{l}} =\left| l_1-l_2\right| \\ {\hat{l}},\text {even} \end{array}}^{l_1 + l_2} \left| \alpha _{{\hat{l}}}\right| \\&\le \frac{\sqrt{2}}{4}\left( c_{2B-4} - c_{2}\right) . \end{aligned} \end{aligned}$$

(23)

The first inequality is derived by using the triangle inequality and the increasing property of the sum of equispaced samples of Legendre polynomials in Lemma 2, i.e., $c_2 \le c_4 \le c_6 \le \cdots \le c_{2B-4}$. The last inequality also holds by the Cauchy–Schwarz inequality of $\alpha _{{\hat{l}}} = (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -n &{}\quad n &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -k &{}\quad k &{}\quad 0 \end{pmatrix}$.

To be precise, for $-\text {min}\left( l_1,l_2\right) \le k \ne n \le \text {min}\left( l_1,l_2\right)$ one can write

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| \\ {\hat{l}},\text {even} \end{array}}^{l_1 + l_2}\left| (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -n &{}\quad n &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -k &{}\quad k &{}\quad 0 \end{pmatrix}\right| \le \frac{1}{\sqrt{2}}, \end{aligned} \end{aligned}$$

where $\sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| \\ {\hat{l}},\text {even} \end{array}}^{l_1 + l_2} (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2= 1$ and $\sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| \\ {\hat{l}},\text {even} \end{array}}^{l_1 + l_2}(2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -k &{}\quad k &{}\quad 0 \end{pmatrix}^2= \frac{1}{2}$ as a consequence of Lemma 4.

For $\tau = k = n \ne 0$ and $-\text {min}\left( l_1,l_2\right) \le \tau \le \text {min}\left( l_1,l_2\right)$, write $\beta _{{\hat{l}}} =(2{\hat{l}} + 1) \begin{pmatrix} l_1&{}\quad l_2&{}\quad {\hat{l}} \\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2$. The product $\left| \sum _{p=1}^m \mathrm {d}_{l_1}^{\tau ,\tau }(\cos \theta _p) \mathrm {d}_{l_2}^{\tau ,\tau }(\cos \theta _p)\right|$ can be upper-bounded as

$$\begin{aligned} \begin{aligned} \left| \sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| \\ {\hat{l}},\text {even} \end{array}}^{l_1 + l_2} c_{{\hat{l}}}\beta _{{\hat{l}}}\right|&\le c_{2B-4}\sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| \\ {\hat{l}},\text {even} \end{array}}^{l_1 + l_2}\beta _{{\hat{l}}} = \frac{c_{2B-4}}{2}. \end{aligned} \end{aligned}$$

(24)

The maximum of $c_{{\hat{l}}}$ is derived from the increasing property of the sum of equispaced samples of Legendre polynomials in Lemma 2, i.e., $0 \le c_2 \le c_4 \le c_6 \le \cdots \le c_{2B-4}$, and for $1\le \left| k\right| =\left| n\right| =\left| \tau \right| \le \text {min}(l_1,l_2)$, the sum of Wigner 3j symbols $\sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| \\ {\hat{l}},\text {even} \end{array}}^{l_1 + l_2}\beta _{{\hat{l}}} = \sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| \\ {\hat{l}},\text {even} \end{array}}^{l_1 + l_2}(2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2 = \frac{1}{2}$ as the result from Lemma 4. Therefore, from (23) and (24), it is enough to consider the upper bound in (24). We then need to show

$$\begin{aligned} \left| \sum _{p=1}^{m} P_{B-1}(\cos \theta _p) P_{B-3}(\cos \theta _p)\right| - \frac{1}{2}\sum _{p=1}^{m} {P}_{2B-4}(\cos \theta _p) \ge 0. \end{aligned}$$

(25)

We have product of two Legendre polynomials $\left| \sum _{p=1}^m P_{B-3}(\cos \theta _p) P_{B-1}(\cos \theta _p)\right|$ as

$$\begin{aligned} \left| \sum _{\begin{array}{c} {{\hat{l}}}=2\\ {\hat{l}}, \text {even} \end{array}}^{2B-4} (2{\hat{l}} + 1) \begin{pmatrix} B-3&{}\quad B-1&{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2\sum _{p=1}^m P_{{\hat{l}}} (\cos \theta _p)\right| . \end{aligned}$$

Suppose that we have $\rho _{{\hat{l}}} = (2{\hat{l}} + 1) \begin{pmatrix} B-3 &{}\quad B-1&{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$ then we have to show $\sum _{\begin{array}{c} {\hat{l}}=2\\ {{\hat{l}}},\text {even} \end{array}}^{2B-4} \rho _{{\hat{l}}}c_{{\hat{l}}} - \frac{c_{2B-4}}{2} \ge 0$. From Lemma 1 and for even ${\hat{l}}$, we have $c_{{{\hat{l}}}}=\sum _{p=1}^m P_{{\hat{l}}} (\cos \theta _p) = 1 + \frac{{{\hat{l}}}({{\hat{l}}}+1)}{6(m-1)} + R_{{{\hat{l}}}}(m)$, where from Proposition 2 the interval of the residual is given as $-0.463< R_{{\hat{l}}}(m) < 0$. Finally, we can write

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} {\hat{l}}=2\\ {{\hat{l}}},\text {even} \end{array}}^{2B-4} \rho _{{\hat{l}}}c_{{\hat{l}}}&= \sum _{\begin{array}{c} {\hat{l}}=2\\ {{\hat{l}}},\text {even} \end{array}}^{2B-4} \rho _{{\hat{l}}}\left( 1 + \frac{{\hat{l}}({\hat{l}}+1)}{6(m-1)} + R_{{\hat{l}}}(m)\right)&\ge \sum _{\begin{array}{c} {\hat{l}}=2\\ {{\hat{l}}},\text {even} \end{array}}^{2B-4} \rho _{{\hat{l}}}\left( 0.537 + \frac{{\hat{l}}({\hat{l}}+1)}{6(m-1)}\right) . \end{aligned} \end{aligned}$$

Additionally, we can bound $\frac{c_{2B-4}}{2}$ as

$$\begin{aligned} \begin{aligned} \frac{c_{2B-4}}{2}&= \frac{1}{2}\left( 1\!+\! \frac{(2B-4)(2B-3)}{6(m-1)} \!+\! R_{\hat{2B-4}}(m)\right)&\le \! \frac{1}{2}\left( 1+ \frac{(2B-4)(2B-3)}{6(m-1)}\right) \end{aligned} \end{aligned}$$

Therefore, the lower bound can be derived as $\sum _{\begin{array}{c} {\hat{l}}=2\\ {{\hat{l}}},\text {even} \end{array}}^{2B-4} \rho _{{\hat{l}}}c_{{\hat{l}}} - \frac{c_{2B-4}}{2} \ge {\hat{C}} + \frac{B}{6(m-1)} > 0$.

The constant ${\hat{C}}$ is obtained from $0.537 \sum _{\begin{array}{c} {\hat{l}}=2\\ {{\hat{l}}}\text {even} \end{array}}^{2B-4} \rho _{{\hat{l}}} - \frac{1}{2} = 0.537 - 0.5 > 0$, since $\sum _{\begin{array}{c} {\hat{l}}=2\\ {{\hat{l}}},\text {even} \end{array}}^{2B-4} \rho _{{\hat{l}}} = 1$ as a consequence of (14). The last term $\frac{B}{6(m-1)}$ is deduced from Corollary 2, where $\sum _{\begin{array}{c} {\hat{l}}=2 \\ {\hat{l}}, \text {even} \end{array}}^{2B -4} \rho _{{\hat{l}}}({\hat{l}}^2 + {\hat{l}}) = 2 + 2(B-1)(B-2)$. Therefore, we have shown that the maximum is attained by the product of two Legendre polynomials for degrees $l_1 = B-3$ and $l_2 = B-1$. $\square$

9 Proofs of lemmas and proposition

9.1 Proofs of lemmas in Sect. 4

Proof of Lemma 1

The proof utilizes the characterization of Legendre polynomials given in (47). Note that Legendre polynomials of even degrees are even functions. For $l = 0$, this summation is equal to m regardless of how we sample the Legendre polynomials. Thus, the analysis is started for even degrees $l \ge 2$, and the samples are given by $\cos \theta _p = x_p=\frac{2p-m-1}{m-1}$ for $p \in [m]$. Since the Legendre polynomials are even for even degrees, and these sample points are symmetric on the interval $[-1,1]$, it is enough to only consider the positive samples. We first assume that m is odd with ${\widetilde{m}}=(m-1)/2$,

$$\begin{aligned} \begin{aligned} \sum _{p=1}^{{m}}P_l(x_p)&= 2\sum _{p=1}^{{\widetilde{m}}}P_l(y_p)+ P_l(0), \end{aligned} \end{aligned}$$

(26)

where the samples in (0, 1] are given by $y_p = \frac{p}{{\widetilde{m}}}$ for $p \in [{\widetilde{m}}]$. By using the definition of Legendre polynomials in (47) and Bernoulli summation in (51), we can write:

$$\begin{aligned} \sum _{p=1}^{{\widetilde{m}}}P_l(y_p)&= 2^l \sum _{k=0}^{l} \left( {\begin{array}{c}l\\ k\end{array}}\right) \left( {\begin{array}{c}\frac{l+k-1}{2}\\ l\end{array}}\right) \left( \frac{1}{k+1}\sum _{j=0}^k{B_j}\left( {\begin{array}{c}k+1\\ j\end{array}}\right) {\widetilde{m}}^{1-j}\right) \\&{= 2^l \sum _{j=0}^l {B_j}{\widetilde{m}}^{1-j} \left( \sum _{k=j}^{l} \left( {\begin{array}{c}l\\ k\end{array}}\right) \left( {\begin{array}{c}\frac{l+k-1}{2}\\ l\end{array}}\right) \frac{1}{k+1}\left( {\begin{array}{c}k+1\\ j\end{array}}\right) \right) }. \end{aligned}$$

We start by simplifying the first terms of the sum given by $j=0,1,2$. For $j=0$ and from Bernoulli number $B_0 = 1$, Table (10.3.1), the first term is given by:

$$\begin{aligned} \begin{aligned} 2^l \sum _{k=0}^{l} \left( {\begin{array}{c}l\\ k\end{array}}\right) \left( {\begin{array}{c}\frac{l+k-1}{2}\\ l\end{array}}\right) \frac{{\widetilde{m}}}{k+1}&= 2^l \sum _{k=0}^{l} \left( {\begin{array}{c}l\\ k\end{array}}\right) \left( {\begin{array}{c}\frac{l+k-1}{2}\\ l\end{array}}\right) \int _{0}^{1} {\widetilde{m}}x^{k} dx\\&=\int _{0}^{1}P_l(x) \mathrm dx = \frac{1}{2} \int _{-1}^{1}P_l(x) \mathrm dx=0 \end{aligned} \end{aligned}$$

The last equality holds from the definition of Legendre polynomials in (47) and integration of Legendre polynomials on the interval $[-1,1]$, which is equal to 0 for $l\ne 0$ as in (46).

For $j=1$ and using Bernoulli number $B_1 = \frac{1}{2}$, we have the following identity

$$\begin{aligned} \begin{aligned} 2^{l-1} \sum _{k=1}^{l} \left( {\begin{array}{c}l\\ k\end{array}}\right) \left( {\begin{array}{c}\frac{l+k-1}{2}\\ l\end{array}}\right) =\frac{P_l(1) - P_l(0)}{2}, \end{aligned} \end{aligned}$$

(27)

where the equality is derived by using expansion of Legendre polynomials in (47) and substitute $x=1$. For even degree l and $k=0$, we have $P_l(1) = 1$ and $P_l(0)$, respectively (see (48)). Hence, the second sum is equal to $\frac{1 - P_l(0)}{2}$.

For $j=2$ , the summation is then obtained by using Bernoulli number $B_2=\frac{1}{6}$ and the derivative of Legendre polynomials in (49)

$$\begin{aligned} \begin{aligned} \sum _{k=2}^{l}2^l \left( {\begin{array}{c}l\\ k\end{array}}\right) \left( {\begin{array}{c}\frac{l+k-1}{2}\\ l\end{array}}\right) \frac{k}{12{\widetilde{m}}} =\frac{1}{12{\widetilde{m}}} \left. \frac{\mathrm {d}P_{l}(x)}{\mathrm {d}x} \right| _{x=1} = \frac{1}{12{\widetilde{m}}} \frac{l(l+1)}{2}. \end{aligned} \end{aligned}$$

The final sum can be obtained as

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{m}P_l(x_i) =2\sum _{i=0}^{{\widetilde{m}}}P_l(y_i) + P_l(0) =1+\frac{l(l+1)}{6(m-1)}+ R_l(m), \end{aligned} \end{aligned}$$

where we use the fact that ${\widetilde{m}} = \frac{m-1}{2}$. The remainder term of the summation, $R_l(m)$, can be expressed as

$$\begin{aligned} \begin{aligned} R_l(m) = 2^{l+1} \sum _{k=3}^{l} \left( {\begin{array}{c}l\\ k\end{array}}\right) \left( {\begin{array}{c}\frac{l+k-1}{2}\\ l\end{array}}\right) \left( {\frac{1}{k+1}\sum _{j=3}^k{B_j}\left( {\begin{array}{c}k+1\\ j\end{array}}\right) \left( \frac{m-1}{2}\right) ^{1-j}}\right) . \end{aligned} \end{aligned}$$

For $j \ge 3$, the Bernoulli number is non-zero only for even values of j, as discussed in Table (10.3.1). By changing the summation index, we have $R_l(m)$ as

$$\begin{aligned} {R_l(m)=}&\sum _{\begin{array}{c} j=4 \\ j,\text {even} \end{array}}^{l} B_j \frac{2^j}{j! (m-1)^{j-1}} 2^{l}\sum _{k=j}^l \left( {\begin{array}{c}l\\ k\end{array}}\right) \left( {\begin{array}{c}\frac{l+k-1}{2}\\ l\end{array}}\right) \frac{k!}{(k+1-j)!}. \end{aligned}$$

From (49), (50) and the relation between Bernoulli number and zeta function in (52), we have

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} j=4 \\ j,\text {even} \end{array}}^{l} \frac{\zeta (j) (l + j -1)! 4 }{(j-1)!(l-j+1)! (2\pi )^j} \frac{(-1)^{\frac{j}{2} +1}}{(m-1)^{j-1}}= \sum _{\begin{array}{c} j=4 \\ j,\text {even} \end{array}}^{l}\frac{(-1)^{\frac{j}{2} + 1}S_l^j}{(m-1)^{j-1}}.\\ \end{aligned} \end{aligned}$$

Now consider $j=2$ for the last equation with the value of $\zeta (2) = \frac{ \pi ^2}{6}$, then the equation is equal to

$$\begin{aligned} \frac{\zeta (2) (l + 1)! 4 }{ (l- 1)! (2\pi )^2} \frac{1}{(m-1)} = \frac{ \zeta (2)(l+1)l}{\pi ^2 (m-1)} = \frac{l(l+1)}{6(m-1)}, \end{aligned}$$

(28)

which completes the claim. The same approach can be used to derive the result for even m. $\square$

9.2 Proof of proposition in Sect. 4

Proof of Proposition  2

From Lemma 1, the sum of equispaced samples Legendre polynomials can be written as

$$\begin{aligned} \begin{aligned} \sum _{p=1}^m P_l(\cos \theta _p) = 1 + \frac{l(l+1)}{6(m-1)} + R_l(m) , \end{aligned} \end{aligned}$$

where $R_l(m) = \sum _{\begin{array}{c} j= 4\\ j,\text {even} \end{array}}^{l}\frac{(-1)^{\frac{j}{2} + 1}S_l^j}{(m-1)^{j-1}}$ with $S_l^j = \frac{\zeta (j) (l+j-1)! 4 }{(j-1)! (l-j+1)! (2\pi )^j} > 0$ . We want to show that the sequence of residuals $\frac{S_l^j}{(m-1)^{j-1}}$ is decreasing with increasing even $j \ge 4$. In other words, we want to show $\frac{S_l^j}{(m-1)^{j-1}} \ge \frac{S_l^{j+2}}{(m-1)^{j+1}}$ and write the ratio as

$$\begin{aligned} \begin{aligned} \frac{S_l^{j+2} }{S_l^j (m-1)^{2}}&= \frac{\zeta (j+2) (l-j+1)(l-j)(l+j+1)(l+j)}{\zeta (j) (j+1)(j) ((m-1)2\pi )^2}\\&<\frac{(l^2-j^2)\left( (l^2-j^2) + 2l + 1\right) }{(j+1)(j) ((m-1)2\pi )^2}, \end{aligned} \end{aligned}$$

(29)

where the upper bound is derived from the fact that the zeta function is decreasing for an increasing even j, that is $\zeta (j) > \zeta (j+2)$. In order to show the decreasing property, it should be enough to show that the ratio above is upper bounded by 1, which is accomplished by considering $m - 1 \ge \frac{(l+1)^2}{10}$ for $4 \le j_{,\text {even}} \le l$ and $l \ge 4$.

We want to show the lower bound of $R_l(m)$. For an even $\frac{l}{2}$, we will have $R_l(m)$ as $-\frac{ S_l^4}{(m-1)^{3}} + \left( \frac{ S_l^6}{(m-1)^{5}}- \frac{S_l^8}{(m-1)^{7}} \right) + \cdots + \left( \frac{S_l^{l-2}}{(m-1)^{l-3}} -\frac{S_l^l}{(m-1)^{l-1}} \right) \ge -\frac{ S_l^4}{(m-1)^{3}}.$ The lower bound holds because $\frac{S_l^l}{(m-1)^{l-1}}$ is decreasing. Therefore, the subtractions in the bracket are positive. Using the geometric-arithmetic mean inequality $\frac{(l+k)!}{(l-k)!} \le (l+1)^{2k}$ [26, eq.15], we have $-\frac{ S_l^4}{(m-1)^{3}} = -\frac{\zeta (4)(l+3)!4.10^3}{3!(l-3)!(2\pi )^4 (l+1)^6} > -0.463.$

The same approach can be used for an odd $\frac{l}{2}$. The difference is that, instead of having two terms for $l-2$ and l at the end, we only have l, which is positive because $(-1)^{\frac{l}{2} + 1}$ is positive for an odd $\frac{l}{2}$. Thus, it does not change the lower bound.

It remains to show the upper bound. For an even $\frac{l}{2}$, this follows by simply re-writing the sum $R_l(m)$ as $+ \left( \frac{ S_l^6}{(m-1)^{5}}- \frac{ S_l^4}{(m-1)^{3}} \right) + \cdots -\frac{S_l^l}{(m-1)^{l-1}}$. Since each difference is negative, $R_l(m)$ is negative in general. A similar argument holds for odd $\frac{l}{2}$. $\square$

Proof of Lemma 2

For $l=2$, it is proven in Lemma 1 that $\sum _{p=1}^m P_l(\cos \theta _p) = 1 + \frac{l(l+1)}{6(m-1)} > 0$. Therefore, we have $\sum _{p=1}^m P_4(\cos \theta _p) - \sum _{p=1}^m P_2(\cos \theta _p) = \frac{7}{3(m-1)} + R_4(m) =\frac{7}{3(m-1)} -\frac{7}{3(m-1)^3} \ge 0$, where $R_l(m)=\sum _{\begin{array}{c} j = 4 \\ j, \text {even} \end{array}}^l \frac{(-1)^{\frac{j}{2} + 1}S_l^j}{(m-1)^{j-1}}$ and $S_l^j = \frac{\zeta (j) (l+j-1)! 4 }{(j-1)! (l-j+1)! (2\pi )^j}$. Therefore, we only need to prove the statement for even $l \ge 4$. The increasing property of the summations, $\sum _{p=1}^m P_2(\cos \theta _p)< \sum _{p=1}^m P_4(\cos \theta _p)< \cdots < \sum _{p=1}^m P_{l, \text {even}}(\cos \theta _p)$, directly implies a non-negative property of the sum of equispaced samples Legendre polynomials. Since we compare $l+2$ to l, then the number of sample $m-1 \ge \frac{(l+3)^2}{10}$ should be considered, which means that for even $l \ge 4$, it is enough to show $\sum _{p=1}^m P_{l+2}(\cos \theta _p) - \sum _{p=1}^m P_l(\cos \theta _p) \ge 0$. By using the result from Lemma 1, the condition is equal to $\frac{2l+3}{3} \ge (m-1)\bigg (R_l(m) - R_{l+2}(m) \bigg )$.

Consider the residual $(m-1)(R_l(m) - R_{l+2}(m) )$ and write it as

$$\begin{aligned} \begin{aligned}\sum _{\begin{array}{c} j=4 \\ j, \text {even} \end{array}}^{l} \frac{(-1)^{\frac{j}{2}} \left( S_{l+2}^j - S_{l}^j\right) }{(m-1)^{j-2}} - \frac{(-1)^{\frac{l+2}{2} + 1}S_{l+2}^{l+2}}{(m-1)^{l}}. \end{aligned} \end{aligned}$$

(30)

First of all, we show that $\frac{\left( S_{l+2}^j - S_{l}^j\right) }{(m-1)^{j-2}}$ is positive for a fix m. This immediately follows from the following inequality:

$$\begin{aligned} \frac{S_{l+2}^j}{S_{l}^j} = \frac{(l+j+1)(l+j)}{(l-j+3)(l-j+2)} > 1. \end{aligned}$$

(31)

Second of all, the sequence $\frac{\left( S_{l+2}^j - S_{l}^j\right) }{(m-1)^{j-2}}$ is decreasing if we increase even j, or we have $\frac{\big (S_{l+2}^j - S_{l}^j\big )}{(m-1)^{j-2}} > \frac{\big (S_{l+2}^{j+2} - S_{l}^{j+2}\big )}{(m-1)^{j}}.$ Therefore, it is enough to show that the inequality $\frac{\left( S_{l+2}^{j+2} - S_{l}^{j+2}\right) }{\left( S_{l+2}^j - S_{l}^j\right) (m-1)^{2}}< 1$ holds for $m-1 \ge \frac{(l+3)^2}{10}$. Let’s expand this ratio by using (31) as

$$\begin{aligned} \begin{aligned} \frac{\left( S_{l+2}^{j+2} - S_{l}^{j+2}\right) }{\left( S_{l+2}^j - S_{l}^j\right) (m-1)^{2}} = \frac{S_l^{j+2} \big ( \frac{(l+j+3)(l+j+2)}{(l-j+1)(l-j)}- 1\big )}{S_l^j \big (\frac{(l+j+1)(l+j)}{(l-j+3)(l-j+2)}- 1\big ) (m-1)^{2}} \end{aligned} \end{aligned}$$

(32)

From (29), we know the ratio $\frac{S_l^{j+2}}{S_l^j (m-1)^2}$. Hence, (32) can be expressed as

$$\begin{aligned} \begin{aligned}&\frac{S_l^{j+2} \big ( \frac{(l+j+3)(l+j+2)}{(l-j+1)(l-j)}- 1\big )}{S_l^j \big (\frac{(l+j+1)(l+j)}{(l-j+3)(l-j+2)}- 1\big ) (m-1)^{2}} \\&\quad = \frac{\zeta (j+2) (l+j+1)(l+j)}{\zeta (j) (j) ((m-1)2\pi )^2}\frac{ (l-j+3)(l-j+2) }{ (j-1)}. \end{aligned} \end{aligned}$$

(33)

Additionally, we have the following inequality:

$$\begin{aligned} \begin{aligned} \frac{\zeta (j+2) (l+j+1)(l+j)}{\zeta (j) (j) ((m-1)2\pi )^2}\frac{ (l-j+3)(l-j+2) }{ (j-1)} < 1. \end{aligned} \end{aligned}$$

(34)

The upper bound follows from the fact that $\zeta (j) > \zeta (j+2)$ and using this condition on the number of samples $m-1 \ge \frac{(l+3)^2}{10}$. Thereby, it proves that for increasing even j, the term $\frac{\big (S_{l+2}^j - S_{l}^j\big )}{(m-1)^{j-2}}$ is decreasing. Summarizing the results in (31) and (33), we have $S^j_{l+2} > S^j_{l}$ and $\left( S^j_{l + 2} - S^j_l\right) (m-1)^2 > \left( S^{j+2}_{l + 2} - S^{j+2}_l\right)$.

Therefore, for even $\frac{l}{2}$, we write

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} j=4 \\ j,\text {even} \end{array}}^{l} \frac{(-1)^{\frac{j}{2}} \left( S_{l+2}^j - S_{l}^j\right) }{(m-1)^{j-2}}&= \frac{\left( S_{l+2}^4 - S_{l}^4\right) }{(m-1)^{2}} -\left( \frac{\left( S_{l+2}^6 - S_{l}^6\right) }{(m-1)^{4}} - \frac{\left( S_{l+2}^8 - S_{l}^8\right) }{(m-1)^{6}} \right) -\cdots \\&\quad -\left( \frac{\left( S_{l+2}^{l-2} - S_{l}^{l-2}\right) }{(m-1)^{l-4}} - \frac{\left( S_{l+2}^l - S_{l}^l\right) }{(m-1)^{l-2}} \right) \le \frac{\left( S_{l+2}^4 - S_{l}^4\right) }{(m-1)^{2}}. \end{aligned} \end{aligned}$$

The upper bound follows because the subtractions in the brackets are positive. It should be noted that the upper bound also holds for an odd $\frac{l}{2}$, where instead of having two terms for $l-2$ and l, we only have l which is negative. Finally, collecting all these results, we can bound (30) with $\frac{\big (S_{l+2}^4 - S_{l}^4\big )}{(m-1)^{2}} + \frac{S_{l+2}^{l+2}}{(m-1)^{l}}$. We want to show this upper bound is smaller than $\frac{2l+3}{3}$.

Let’s first consider the upper bound of $\frac{\big (S_{l+2}^4 - S_{l}^4\big )}{(m-1)^{2}}$. For $m-1 \ge \frac{(l+3)^2}{10}$ and using the ratio in (31), we obtain

$$\begin{aligned} \begin{aligned} \frac{\big (S_{l+2}^4 - S_{l}^4\big )}{(m-1)^{2}} =\frac{S_{l}^4}{(m-1)^2} \bigg ( \frac{12l+18}{(l-1)(l-2)} \bigg )&< \frac{\zeta (4)(24)10^2}{3!(2\pi )^4} \frac{(l+2)(l+1)l (2l+3)}{(l+3)^3}\\&< C_1 (2l+3), \end{aligned} \end{aligned}$$

where the constant $C_1 = 0.2778$ is derived from the fact that $\zeta (4) = \frac{\pi ^4}{90}$ as in Table (10.3.1). From the definition of $S_{l}^{j}$, an upper bound of $\frac{S_{l+2}^{l+2}}{(m-1)^{l}}$ can be determined by

$$\begin{aligned} \frac{S_{l+2}^{l+2}}{(m-1)^{l}} \le \frac{\zeta (l+2)}{\pi ^{2}}\frac{\Big (l+2 + \big (l+1\big )\Big )! }{\Big (l+2 - \big (l+1\big )\Big )!}\left( \frac{5}{\pi }\right) ^l \frac{1}{(l+1)!(l+3)^{2l}} < C_2 (2l+3) \end{aligned}$$

.

The inequality is derived from the geometric-arithmetic mean inequality using inequality $\frac{(l+k)!}{(l-k)!} \le (l+1)^{2k}$ [26, eq.15]. Additionally, by considering even degrees $l \ge 4$, we have $(l+3)^2 < (2l+3) (l+1)$ and $2^l < l!$. Using the decreasing property of the sequence and properties of the zeta function given in Table (10.3.1), the maximum constant $C_2$ is achieved for $l = 4$, which gives $C_2 = 0.0422$.

Combining the results, we complete the proof $(m-1) (R_l(m) - R_{l+2}(m) ) \le (C_1 + C_2) (2l+3) < \frac{(2l+3)}{3}$. Thus, $\sum _{p=1}^m P_{l+2}(\cos \theta _p) - \sum _{p=1}^m P_l(\cos \theta _p) \ge 0$. $\square$

9.3 Proofs of lemmas in Sect. 5

Proof of Lemma 3

In (56), we have the exact expression for Wigner 3j symbols $\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}$, where $2L = l_1 + l_2 + l_3$.

The ratio between $\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$ and $\begin{pmatrix} l_1+1 &{}\quad l_2+1 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$ can be written as

$$\begin{aligned} \begin{aligned} \frac{(2L+3)!(2L-2l_3)!}{(2L+1)!(2L+2-2l_3)!}\biggl (\frac{L!(L+1-l_3)!}{(L+1)!(L-l_3)!}\biggr )^2 = \frac{(2L+3)(2L-2l_3+2)}{(2L+2)(2L-2l_3+1)}\ge 1. \end{aligned}\nonumber \\ \end{aligned}$$

(35)

Therefore, it proves the first property $\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2 \ge \begin{pmatrix} l_1+1 &{}\quad l_2+1 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$. Similarly, for the second condition we can write the ratio between $\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$ and $\begin{pmatrix} l_1+2 &{}\quad l_2 &{}\quad l_3 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$ as $\frac{(L+\frac{3}{2})(L-l_3+1)}{(L+1)(L-l_3 +\frac{1}{2}) }\frac{(L-l_2+1)(L-l_1-\frac{1}{2})}{(L-l_2+\frac{1}{2})(L-l_1)}$. The last ratio can be written as $\frac{ L^2-Ll_1-Ll_2 +l_1l_2 + \frac{L}{2} +\frac{l_2}{2} - l_1 -\frac{1}{2}}{L^2-Ll_1 -Ll_2+l_1l_2+\frac{L}{2} - \frac{l_1}{2}}$. This ratio is greater than one, if we have $l_2 \ge l_1 +1 > l_1$. This condition holds based on the assumption of the lemma. . $\square$

Proof of Lemma 4

Let’s rewrite the product of Wigner d-functions as in (15) for an arbitrary sample and $-\text {min}(l_1,l_2) \le k \ne n \le \text {min}(l_1,l_2)$

$$\begin{aligned} \begin{aligned} \left| \mathrm {d}_{l_1}^{k ,n }(\cos \theta ) \mathrm {d}_{l_2}^{k ,n }(\cos \theta )\right| = \left| \sum _{{\hat{l}}=\left| l_1 - l_2\right| }^{l_1 + l_2} (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -k &{}\quad k &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -n &{}\quad n &{}\quad 0 \end{pmatrix}P_{{\hat{l}}} (\cos \theta )\right| . \end{aligned}\nonumber \\ \end{aligned}$$

(36)

Suppose that we have $\theta = 0$. From the definition of Wigner d-functions in (2), we have the weight $\sin ^{\xi } \left( \frac{0}{2} \right) = 0$ and therefore $\mathrm {d}_{l}^{k ,n }(\cos 0) = 0$. On the contrary, the Legendre polynomials become $P_{{{\hat{l}}}}(1) = 1$ for even and odd degrees ${{\hat{l}}}$ [2, Chapter.22 Orthogonal Polynomials, Eq. 22.2.10]. Therefore, we have

$$\begin{aligned} \begin{aligned}&\sum _{{\hat{l}},\text {even}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -k &{}\quad k &{}\quad 0 \end{pmatrix}\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -n &{}\quad n &{}\quad 0 \end{pmatrix}\\&\quad + \sum _{{\hat{l}},\text {odd}} (2{\hat{l}}+1)\begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -k &{}\quad k &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -n &{}\quad n &{}\quad 0 \end{pmatrix}=0, \end{aligned} \end{aligned}$$

(37)

which is obvious because of the orthogonality of Wigner 3j symbols as discussed in (14).

In contrast, if we consider $\theta = \pi$, we have the weight $\cos ^{\lambda } \left( \frac{\pi }{2} \right) = 0$ and hence $\mathrm {d}_{l}^{k ,n }(\cos \pi ) = 0$. From symmetry of the Legendre polynomials we have $P_{{{\hat{l}}}}(-1) = 1$ for even degrees ${{{\hat{l}}}}$ and $P_{{{\hat{l}}}}(-1) = -1$ for odd degrees ${\hat{l}}$. Hence, we obtain

$$\begin{aligned} \begin{aligned}&\sum _{{\hat{l}}, \text {even}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -k &{}\quad k &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -n &{}\quad n &{}\quad 0 \end{pmatrix} \\&\quad = \sum _{{\hat{l}}, \text {odd}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -k &{}\quad k &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -n &{}\quad n &{}\quad 0 \end{pmatrix}. \end{aligned} \end{aligned}$$

(38)

Using (37) and (38), we complete the proof

$$\begin{aligned} \begin{aligned}&\sum _{{\hat{l}}, \text {even}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -k &{}\quad k &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -n &{}\quad n &{}\quad 0 \end{pmatrix}\\&\quad = \sum _{{\hat{l}}, \text {odd}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -k &{}\quad k &{}\quad 0 \end{pmatrix} \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -n &{}\quad n &{}\quad 0 \end{pmatrix} = 0. \end{aligned} \end{aligned}$$

(39)

For the case $k=n=\tau$ and $1 \le \left| \tau \right| \le \text {min}(l_1,l_2)$, we can express the product of Wigner d-functions as

$$\begin{aligned} \begin{aligned} \left| \mathrm {d}_{l_1}^{\tau ,\tau }(\cos \theta ) \mathrm {d}_{l_2}^{\tau ,\tau }(\cos \theta )\right| = \left| \sum _{{\hat{l}}=\left| l_1 - l_2\right| }^{l_1 + l_2} (2{\hat{l}} + 1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}} \\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2 P_{{\hat{l}}} (\cos \theta )\right| . \end{aligned} \end{aligned}$$

(40)

As discussed earlier, if we choose $\theta = \pi$, then we have

$$\begin{aligned} \begin{aligned} \sum _{{\hat{l}}, \text {even}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2 = \sum _{{\hat{l}}, \text {odd}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2. \end{aligned} \end{aligned}$$

However, we know that the sum of squared Wigner 3j symbols for all ${\hat{l}}$ is 1, due to the orthogonal property in (14), i.e., $\sum _{{\hat{l}}=\left| l_1 - l_2\right| }^{l_1 +l_2} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2 = 1$. Thus, we have sum for all even ${{\hat{l}}}$ or odd ${{\hat{l}}}$ as $\sum _{{\hat{l}}, \text {even}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad \quad l_2 &{}\quad {\hat{l}}\\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2 = \sum _{{\hat{l}}, \text {odd}} (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_2 &{}\quad {\hat{l}}\\ -\tau &{}\quad \tau &{}\quad 0 \end{pmatrix}^2 = \frac{1}{2}$. $\square$

Proof of Lemma 5

We first define $b^{(l_1 )}_{{\hat{l}}} = (2{\hat{l}}+1) \begin{pmatrix} l_1 &{}\quad l_1+2 &{}\quad {\hat{l}}\\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$. For increasing index $l_1$, we prove this lemma by using inductions.

For $l_1 = 0$, the result is $2+2(l_1 + 2)(l_1 +1) = 6$. The summation can be written as $\sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| =2 \\ {\hat{l}},\text {even} \end{array}}^{2} b^{(l_1 = 0)}_{{\hat{l}}}({\hat{l}}^2 + {\hat{l}}) = b^{(l_1=0)}_2 6 = 6$, which is true because of the orthogonal property of Wigner 3j symbols, as discussed in (14), $\sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| =2 \\ {\hat{l}},\text {even} \end{array}}^{2l_1 + 2} b_{{\hat{l}}} = 1$.

For $l_1 = 1$, we have $2+2(l_1 + 2)(l_1 +1) = 14$. This summation becomes complicated since we have two different values ${\hat{l}}$ for the Wigner 3j symbols,

$$\begin{aligned} \sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| =2 \\ {\hat{l}},\text {even} \end{array}}^{4} b^{(l_1 = 1)}_{{\hat{l}}}({\hat{l}}^2 + {\hat{l}}) = b^{(l_1=1)}_2 6 + b^{(l_1=1)}_4 20 \end{aligned}$$

Since we have the ratio between two consecutive Wigner 3j symbols for fixed values of ${\hat{l}}$ as discussed in the proof of Lemma 3 in (35), the relation between two different values $l_1$ for Wigner 3j symbols, $b^{(l_1+1)}_{{\hat{l}}}= {(2{\hat{l}}+1)}\begin{pmatrix} l_1 + 1 &{}\quad l_1 + 3 &{} \quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$ and $b^{(l_1)}_{{\hat{l}}} = {(2{\hat{l}}+1)} \begin{pmatrix} l_1 &{}\quad l_1+2 &{}\quad {\hat{l}} \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}^2$ can be obtained as

$$\begin{aligned} \frac{b^{(l_1+1)}_{{\hat{l}}}}{b^{(l_1)}_{{\hat{l}}}}=\frac{(2l_1+4 + {\hat{l}})(2l_1 + 3 - {\hat{l}})}{(2l_1+5 + {\hat{l}})(2l_1+4 - {\hat{l}})} = C_{{\hat{l}}}^{(l_1)} \end{aligned}$$

(41)

From this relation, we can write $\sum _{\begin{array}{c} {\hat{l}}=\left| l_1-l_2\right| =2 \\ {\hat{l}}, \text {even} \end{array}}^{4} b^{(l_1 = 1)}_{{\hat{l}}}({\hat{l}}^2 + {\hat{l}}) = C_{2}^{(l_1=0)}b^{(l_1=0)}_2 6 + b^{(l_1=1)}_4 20 = \frac{3}{7} 6 + (1 -\frac{3}{7}) 20 = 14$, which is correct for $l_1=1$. The equality is derived from the fact that $C_{2}^{(l_1=0)} = \frac{3}{7}$ and from the previous case, $l_1 = 0$, we have $b^{(l_1=0)}_2 = 1$. Additionally, from (14), the summation is $b_2^{(l_1=1)} + b_4^{(l_1=1)} = 1$.

We generalize the induction part and consider the assumption for $l_1 = k$

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} {\hat{l}}= 2 \\ {\hat{l}}, \text {even} \end{array}}^{2k + 2} b^{(l_1 = k)}_{{\hat{l}}}({\hat{l}}^2 + {\hat{l}}) = 2 + 2(k+2)(k +1). \end{aligned} \end{aligned}$$

(42)

Therefore, we can determine the induction part to observe

$$\begin{aligned} \sum _{\begin{array}{c} {\hat{l}}= 2 \\ {\hat{l}}, \text {even} \end{array}}^{2k + 2} b^{(l_1 + 1 =k+1)}_{{\hat{l}}}({\hat{l}}^2 + {\hat{l}}) + b^{(l_1 + 1 =k+1)}_{2k+4}\left( (2k+4)^2 + (2k +4)\right) \end{aligned}$$

From (14) and (41), we can write above summation as

$$\begin{aligned} \sum _{\begin{array}{c} {\hat{l}}= 2 \\ {\hat{l}}, \text {even} \end{array}}^{2k + 2} C^{(l_1=k)}_{{\hat{l}}}b^{(l_1=k)}_{{\hat{l}}}({\hat{l}}^2 + {\hat{l}}) + \left( 1 - \sum _{\begin{array}{c} {\hat{l}}= 2 \\ {\hat{l}}, \text {even} \end{array}}^{2k + 2} C^{(l_1=k)}_{{\hat{l}}}b^{(l_1=k)}_{{\hat{l}}}\right) \left( (2k+4)^2 + (2k +4)\right) , \end{aligned}$$

where we have $C^{(l_1=k)}_{{\hat{l}}} = \frac{4k^2 + 14k + 12 - ({\hat{l}}^2 + {\hat{l}})}{4k^2 + 18k + 20-({\hat{l}}^2 + {\hat{l}})}$. Thus, we obtain

$$\begin{aligned} C^{(l_1=k)}_{{\hat{l}}}\left( {\hat{l}}^2 + {\hat{l}} - \left( (2k+4)^2 + (2k +4)\right) \right) = - \left( 4k^2 + 14k + 12 \right) + ({\hat{l}}^2 + {\hat{l}}). \end{aligned}$$

From (42) we have $\sum _{\begin{array}{c} {\hat{l}}= 2 \\ {\hat{l}}, \text {even} \end{array}}^{2k + 2} b^{(l_1 = k)}_{{\hat{l}}}({\hat{l}}^2 + {\hat{l}}) = 2 + 2(k+2)(k +1)$. Combining these results and property Wigner 3j symbols in (14), we can write the summation as $\big (4k + 8\big ) + 2 + 2(k+2)(k+1)= 2 + 2(k+3)(k+2)$ and complete the proof.

$\square$

9.4 A remark on norms of the columns

The focus of our derivations has been on the inner product of the columns without the normalization. In this section, we study more closely the $\ell _2$-norm of the columns and provide some indications of why these norms do not contribute to the main inequality. An approximation of the $\ell _2$-norm of equispaced samples Wigner d-functions is given in the following lemma.

Lemma 6

Consider a vector of sampled Wigner d-functions $\mathrm {d}_{l}^{k,n}(\cos \varvec{\theta }):=\left( \mathrm {d}_{l}^{k,n}(\cos \theta _1),\dots ,\mathrm {d}_{l}^{k,n}(\cos \theta _m)\right) ^T$ with sampling points as in (12). The $\ell _2$-norm of this vector can be approximated by:

$$\begin{aligned} \left\| \mathrm {d}_{l}^{k,n}(\cos \varvec{\theta })\right\| _2^2 = \frac{m-1}{2l+1} + D_1(k,n) + \mathcal {O}(m^{-1}), \end{aligned}$$

where

$$\begin{aligned} D_1(k,n)=\frac{\left| \mathrm {d}^{k,n}_l(1)\right| ^2 + \left| \mathrm {d}^{k,n}_l(-1)\right| ^2}{2} = {\left\{ \begin{array}{ll} \frac{1}{2} &{}\quad \text {for } {k}= {n} \ne 0 \\ 1 &{}\quad \text {for } k = n =0 \\ 0 &{} \quad \text {for } {k} \ne {n}. \end{array}\right. } \end{aligned}$$

(43)

Proof of Lemma 6

Wigner d-functions are continuous and integrable on the interval $[-1,1]$. The sampling points $x_p = \cos \theta _p = \frac{2(p-1)}{m-1}-1$ for $p \in [m]$ divide the interval $[-1,1]$ into intervals of length $\varDelta _x = \frac{2}{m-1}$. Therefore, we can write the summation in the expression of $\ell _2$-norm, namely $\sum _{p=1}^m \left| \mathrm {d}^{k,n}_l(x_p)\right| ^2$, using trapezoidal rule, as the Riemannian sum approximation of the integral of Wigner d-functions over the interval $[-1, 1]$. First see that

$$\begin{aligned} \begin{aligned}&\varDelta _x\Bigg (\frac{\big |\mathrm {d}^{k,n}_l(1)\big |^2 + \big |\mathrm {d}^{k,n}_l(-1)\big |^2}{2} + \sum _{p=2}^{m-1} \big |\mathrm {d}^{k,n}_l\big ((p-1)\varDelta _x -1\big )\big |^2\Bigg )\\ {}&\quad = \varDelta _x\Bigg (\left\| \mathrm {d}_l^{k,n}({\varvec{x}})\right\| _2^2 - D_1(k,n)\Bigg ),\\ \end{aligned} \end{aligned}$$

where $D_1(k,n) = \frac{\big |\mathrm {d}^{k,n}_l(1)\big |^2 + \big |\mathrm {d}^{k,n}_l(-1)\big |^2}{2}$. It is well known that the integral of squared Wigner d-functions, as in (5), is given by

$$\begin{aligned} \begin{aligned} \int _{-1}^1 \big |\mathrm {d}^{k,n}_l(x)\big |^2 dx= \frac{2}{2l+1}. \end{aligned} \end{aligned}$$

Thereby, the approximation error can be written as

$$\begin{aligned} \begin{aligned}&\left| \int _{-1}^1 \big |\mathrm {d}^{k,n}_l(x)\big |^2 dx - \varDelta _x\left( \left\| \mathrm {d}_l^{k,n}({\varvec{x}})\right\| _2^2 - D_1(k,n)\right) \right| \\&\quad ={\varDelta _x} \left| \frac{m-1}{2l+1} + D_1(k,n) - \left\| \mathrm {d}_l^{k,n}({\varvec{x}})\right\| _2^2\right| = \mathcal {O}(m^{-1}), \\ \end{aligned} \end{aligned}$$

where the $\mathcal {O}(m^{-1})$ is well-known error approximation from the Riemannian sum since we have $\varDelta _x = \frac{2}{m-1}$. Expressed differently, we can write the summation formula as

$$\begin{aligned} \left\| \mathrm {d}_{l}^{k,n}(\cos \varvec{\theta })\right\| _2^2 = \frac{m-1}{2l+1} + D_1(k,n) + \mathcal {O}(m^{-1}). \end{aligned}$$

It is important to have a closed-form expression of $D_1(k,n)$. From (2), we know that the Wigner d-functions are weighted Jacobi polynomials. For several conditions of $-l \le k,n \le l$, we can get different $\xi =\left| k-n\right|$, $\lambda =\left| k+n\right|$, and $\alpha =l-\big (\frac{\xi +\lambda }{2}\big )$ on Jacobi polynomials, which change the value of constant $D_1(k,n)$. Those conditions are given in the following:

• For $k=n=0$, we have $\lambda =\xi =0$ and the Wigner d-function becomes Legendre polynomial $\mathrm {d}_l^{0,0}(\cos \theta ) = P_l(\cos \theta )$. Hence, $\big |\mathrm {d}_l^{0,0}(1)\big |^2 = \big |\mathrm {d}_l^{0,0}(-1)\big |^2 = 1$ because of the symmetry of Legendre polynomials in (45). Therefore, we obtain

  $$\begin{aligned} \left\| P_l(\cos \varvec{\theta })\right\| _2^2 = 1 + \frac{m-1}{2l+1} + \mathcal {O}(m^{-1}). \end{aligned}$$

• For ${k} \ne {n}$, we have $\big |\mathrm {d}_l^{k,n}(1)\big |^2 = \big |\mathrm {d}_l^{k,n}(-1)\big |^2 = D_1(k,n)=0$. This is because for $\theta = 0$ or $\theta = \pi$, the weight of the Wigner d-functions are $\sin ^{\xi } \bigg (\frac{\theta }{2}\bigg ) = 0$ or $\cos ^{\lambda }\bigg (\frac{\theta }{2}\bigg ) = 0$. Hence, we have

  $$\begin{aligned} \left\| \mathrm {d}_{l}^{k,n}(\cos \varvec{\theta })\right\| _2^2 = \frac{m-1}{2l+1} + \mathcal {O}(m^{-1}). \end{aligned}$$

  For a specific case $k=0$ or $n=0$, then $\xi =\lambda$ and the Wigner d-functions become associated Legendre polynomials $\mathrm {d}_l^{k,0}(\cos \theta ) = C_l^k P_l^k(\cos \theta )$, where $C_l^k=\sqrt{\frac{(l-k)!}{(l+k)!}}$, as given in (6). Therefore, the $\ell _2$-norm of associated Legendre polynomials is

  $$\begin{aligned} \left\| C_{l}^kP^k_l(\cos \varvec{\theta })\right\| _2^2 = \frac{m-1}{2l+1} + \mathcal {O}(m^{-1}). \end{aligned}$$

• If ${k}= {n} = {\tau } \ne 0$, then $\xi =0$ and $\lambda = 2\left| \tau \right|$. The Wigner d-functions are $\big |\mathrm {d}_l^{\tau ,\tau }(1)\big |^2 = \big |P_{\alpha }^{0,\lambda }(1)\big |^2 = \left( {\begin{array}{c}\alpha \\ \alpha \end{array}}\right) = 1$ and $\big |\mathrm {d}_l^{\tau ,\tau }(-1)\big |^2=0$ or vice versa, because the weight of the Wigner d-functions are $\cos ^{\lambda } \bigg (\frac{\pi }{2}\bigg ) = 0$ or $\sin ^{\xi } \bigg (\frac{0}{2}\bigg ) = 0$ and due to the property of the Jacobi polynomials in (44). Thus, we have $D_1(k,n)=\frac{1}{2}$.

From those characterizations of $D_1(k,n)$, we complete the proof. $\square$

The proof relies heavily on the definition of the Wigner d-functions in (2) and Jacobi polynomials.

There are some immediate corollaries from this Lemma. First, for equal orders $k=n$, the norm is decreasing in the degree l, which means that the ordering between inner products is preserved after the division. This norm does not have a strong ordering between different degrees and orders (for instance from $k=n=0$ to $k=n\ne 0$). However, the $\ell _2$-norm of Wigner d-functions and associated Legendre polynomials are approximately the same for a sufficiently large m. Note that for large enough m, the norm, after division by m, approaches the functional $L_2$-norm of Wigner d-functions given by $2/(2l+1)$.

10 Appendix

10.1 Derivatives

10.1.1 Derivatives of spherical harmonics

In this article, we implement gradient descent based algorithms to optimize sampling points on the sphere. Therefore, we mention derivatives of spherical harmonics with respect to $\theta$ and $\phi$. These operations are given as follows.

$$\begin{aligned} \begin{aligned} \frac{\partial \mathrm {Y}_{l}^{k} (\theta ,\phi )}{\partial \theta }&= \frac{k \mathrm {Y}_{l}^{k} (\theta ,\phi )}{\tan \theta } + \sqrt{(l-k)(l+k+1)} \mathrm {Y}_{l}^{k+1}(\theta ,\phi ) e^{-i\phi }, \\ \frac{\partial \mathrm {Y}_{l}^{k} (\theta ,\phi )}{\partial \phi }&= ik \mathrm {Y}_{l}^{k}(\theta ,\phi ), \end{aligned} \end{aligned}$$

where the parameters are given in (3). Since we want to minimize the product of two spherical harmonics, the derivative rule for their product is applied.

10.1.2 Derivative of Wigner D-functions

Similar to the spherical harmonics case, the derivatives of Wigner D-function with respect to the $\theta ,\phi$ and $\chi$ are used, as stated below.

$$\begin{aligned} \begin{aligned} \frac{\partial \mathrm {D}_{l}^{k,n}(\theta , \phi ,\chi )}{\partial \theta }&= \left( {\frac{\xi \sin \theta }{2(1 - \cos \theta )}} - {\frac{\lambda \sin \theta }{2(1 + \cos \theta )}} \right) \mathrm {D}_{l}^{k,n} (\theta ,\phi , \chi )\\&- {N_l}\sin \theta \,\omega \sqrt{\gamma }\left( \frac{\xi + \lambda + \alpha + 1}{2}\right) \sin ^{\xi }\left( \frac{\theta }{2} \right) \cos ^{\lambda } \left( \frac{\theta }{2}\right) \\&\times P_{\alpha -1}^{\xi +1,\lambda + 1}(\cos \theta ) e^{-i(k\phi + n\chi )}\\ \frac{\partial \mathrm {D}_{l}^{k,n}(\theta , \phi ,\chi )}{\partial \phi }&= -ik \mathrm {D}_{l}^{k,n}(\theta , \phi , \chi )\,,\\ \frac{\partial \mathrm {D}_{l}^{k,n}(\theta , \phi ,\chi )}{\partial \chi }&= -in\mathrm {D}_{l}^{k,n}(\theta , \phi ,\chi ) \end{aligned} \end{aligned}$$

where the parameters are given in (1). We are using only the last two derivatives for our optimization algorithm. In our setup, $\theta$ is fixed by the grid. It should be noted that, we use chain rule for the derivation with respect to $\theta$, i.e., $\frac{d}{d\theta } f(\cos \theta ) = -\sin \theta \frac{d}{d \cos \theta } f(\cos \theta )$. Additionally, the k-th derivative of Jacobi polynomials is given by

$$\begin{aligned} \frac{d^k}{d \cos ^k \theta } { P_{\alpha } ^{\xi , \lambda } (\cos \theta )} = \frac{\Gamma (\xi + \lambda + \alpha + 1 + k)}{2^k \Gamma (\xi + \lambda + \alpha + 1)} P_{\alpha - k} ^{\xi + k, \lambda + k} (\cos \theta ) \end{aligned}$$

10.2 Hypergeometric polynomials

In this section, we review some important properties of Jacobi and associated Legendre polynomials that are used in this article.

Jacobi polynomials satisfy the following symmetry property:

$$\begin{aligned} P_{\alpha }^{\xi ,\lambda } (-\cos \theta ) = (-1)^{\alpha } P_{\alpha }^{\lambda ,\xi } (\cos \theta ). \end{aligned}$$

(44)

Furthermore, for $\cos \theta = 1$ and $\cos \theta = -1$, we have

$$\begin{aligned} P_{\alpha }^{\xi ,\lambda }(1) = \left( {\begin{array}{c}\alpha + \xi \\ \alpha \end{array}}\right) \quad \text {and} \quad P_{\alpha }^{\xi ,\lambda }(-1) = (-1)^\alpha \left( {\begin{array}{c}\alpha + \lambda \\ \alpha \end{array}}\right) . \end{aligned}$$

Similar to Jacobi polynomials, associated Legendre polynomials have symmetric properties

$$\begin{aligned} \begin{aligned}&P_{l}^k(-x)=(-1)^{k+l}P_l^k(x)\\&P_{l}^{-k}(x)=(-1)^{k}\frac{(l-k)!}{(l+k)!}P_l^k(x). \end{aligned} \end{aligned}$$

(45)

For degree $l = 0$, Legendre polynomials have the property $P_{0}(x) = 1$. Therefore, from the orthogonal property of Legendre polynomials, we also have

$$\begin{aligned} \int _{-1}^{1} {P_{{l}}(x)} \mathrm {d}x= \int _{-1}^{1} P_{0}(x) P_{l}(x) \mathrm {d}x=2\delta _{l0}. \end{aligned}$$

(46)

For $x=1$, the Legendre polynomials $P_l(1)= 1$ [2, Chapter.22 Orthogonal Polynomials, Eq. 22.2.10]. Moreover, for $x=-1$, the property can be generated by a symmetric relation of the Legendre polynomials as in (45) by setting $k=0$. However, for associated Legendre polynomials, we have $P_l^k (1) = {P_l^k(-1)} = 0$ from the following relation

$$\begin{aligned} P_{l}^{k}(x)={(-1)^{k}}(1-x^2)^{k/2}\frac{\mathrm {d}^k}{\mathrm {d} x^k}P_l(x). \end{aligned}$$

Besides using the Rodrigues formula, the Legendre polynomials are also explicitly given as

$$\begin{aligned} P_l(x) = 2^l \sum _{h=0}^{l} \left( {\begin{array}{c}l\\ h\end{array}}\right) \left( {\begin{array}{c}\frac{l+h-1}{2}\\ l\end{array}}\right) x^h. \end{aligned}$$

(47)

In this work, we use this representation to derive the closed-form sum of equispaced samples Legendre polynomials. From (), we can also derive the conditions for $P_l(0)$ for even degree l. For $x = 0$, the expansion is non-zero only when $h = 0$, namely

$$\begin{aligned} \begin{aligned} P_l(0)&= 2^l \left( {\begin{array}{c}l\\ 0\end{array}}\right) \left( {\begin{array}{c}\frac{l-1}{2}\\ l\end{array}}\right) = 2^l \frac{\Gamma \left( \frac{1}{2} + \frac{l}{2} \right) }{\Gamma \left( \frac{1}{2} - \frac{l}{2} \right) l!}= \frac{\left( -1\right) ^{l/2}}{2^l}\left( {\begin{array}{c}l\\ \frac{l}{2}\end{array}}\right) , \end{aligned} \end{aligned}$$

(48)

where we have used properties of gamma function, first $\Gamma (l+1) = l!$ and then the relation

$$\begin{aligned} \begin{aligned} \Gamma \left( \frac{1}{2} + l \right)&= \frac{\left( 2l\right) ! \sqrt{\pi }}{4^l l!}\quad \text {and} \quad \Gamma \left( \frac{1}{2} - l \right)&= \frac{\left( -4 \right) ^l l! \sqrt{\pi }}{\left( 2l\right) !}. \end{aligned} \end{aligned}$$

Another property that is used in this article is the $n-$th derivation of Legendre polynomials. This property can be obtained by using the Gauss hypergeometric function ${}_2F_1(a,b,c,d)$ in [5, p.101] and in [25, eq.22–23]. For $x=1$, the relation can be written as

$$\begin{aligned} \left. \frac{\mathrm {d}^n P_{l}(x)}{\mathrm {d}x^n} \right| _{x=1} = \frac{\Gamma (1 +n + l)}{2^n \Gamma \left( n+ 1\right) \Gamma (1 - n + l)}. \end{aligned}$$

(49)

Apart from the derivative of Gauss hypergeometric function, one can also derive from the explicit representation of Legendre polynomials (47),

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}^{n-1}}{\mathrm {d}x^{n-1}} P_l(x)&=2^l \sum _{h=n-1}^{l} \left( {\begin{array}{c}l\\ h\end{array}}\right) \left( {\begin{array}{c}\frac{l+h-1}{2}\\ l\end{array}}\right) \frac{h!}{(h-n+1)!} x^{h-n+1}.\\ \end{aligned} \end{aligned}$$

For $x=1$, we obtain the following formula

$$\begin{aligned} \begin{aligned} \left. \frac{\mathrm {d}^{n-1}P_l(x)}{\mathrm {d}x^{n-1}} \right| _{x=1}&=2^l \left( {\begin{array}{c}l\\ n-1\end{array}}\right) \left( {\begin{array}{c}\frac{l+n-2}{2}\\ l\end{array}}\right) (n-1)! \\&\quad + 2^l \sum _{h=n }^{l} \left( {\begin{array}{c}l\\ h\end{array}}\right) \left( {\begin{array}{c}\frac{l+h-1}{2}\\ l\end{array}}\right) \frac{h!}{(h-n+1)!}. \end{aligned} \end{aligned}$$

Note that the for $x=1$ and even l,n, the first term is equal to zero. From $n \le l$, and therefore ${\frac{l+n-2}{2}}<{l}$, and using properties of factorials, it follows that $\left( {\begin{array}{c}\frac{l+n-2}{2}\\ l\end{array}}\right) =0$. Thereby, for even l and n, we have

$$\begin{aligned} \begin{aligned} \left. \frac{\mathrm {d}^{n-1} P_l(x)}{\mathrm {d}x^{n-1}}\right| _{x=1}&= 2^l \sum _{h={n} }^{l} \left( {\begin{array}{c}l\\ h\end{array}}\right) \left( {\begin{array}{c}\frac{l+h-1}{2}\\ l\end{array}}\right) \frac{h!}{(h-n+1)!}. \end{aligned} \end{aligned}$$

(50)

10.3 Summations

Several summations have been used in this work, mainly to prove main result, for example the Bernoulli or Faulhaber summation and Abel partial summation. In this section, we will provide a concise summary of these summations.

10.3.1 Bernoulli summation

Suppose that we have the summation $\sum _{p=1}^m p^k$ for integer k. The expression of this summation is originally introduced by Faulhaber until $k = 17$ and later generalized by Bernoulli [20, 23]

$$\begin{aligned} \sum _{p=1}^m p^k = \frac{1}{k+1}\sum _{j=0}^k{B_j}\left( {\begin{array}{c}k+1\\ j\end{array}}\right) {m}^{k+1-j}, \end{aligned}$$

(51)

where $B_j$ is the Bernoulli number. For clarity, we list some of Bernoulli numbers given in the following table⁴

Index (j)	0	1	2	3	4	5	6	7
$B_j$	1	1/2	1/6	0	− 1/30	0	1/42	0

.

It can be seen that for odd $j \ge 3$, the Bernoulli number is equal to zero. This property is useful to prove Lemma 1, Proposition 2, and Lemma 2. Another fascinating property of this number is its close relation with the Riemannian zeta function. We show that the relation for even $j \ge 2$ is

$$\begin{aligned} B_j = \frac{(-1)^{\frac{j}{2}+1} 2 j!}{(2\pi )^j} \zeta (j). \end{aligned}$$

(52)

The zeta function also has an interesting property for some specific values, as given in the following table

Index (j)	2	4	6	8
$\zeta (j)$	$\pi ^2/6$	$\pi ^4/90$	$\pi ^6/945$	$\pi ^8/9450$

It is obvious that for sufficiently large j, the zeta function converges to 1.

10.3.2 Abel partial summation

The Abel partial summation is defined by Niels Henrik Abel [1], which can be considered as discrete counterpart of integration by parts. Suppose we have $n \in \mathbb N$ with sequences $a_1,a_2,\ldots ,a_n$ and also $b_1,b_2,\ldots ,b_n \in \mathbb R$ with $A_p = a_1 + a_2 + \ldots + a_p$, then we have

$$\begin{aligned} \sum _{p=1}^n a_p b_p = A_n b_n + \sum _{p=1}^{n-1} A_p \left( b_p - b_{p+1}\right) . \end{aligned}$$

(53)

10.4 Properties of Wigner 3j symbols

An explicit formula for the general Wigner 3j symbols can be seen in most angular momentum literature. In this paper, the explicit formula for Wigner 3j symbols is taken from [21]

$$\begin{aligned} \begin{aligned} \begin{pmatrix} l_1 &{} l_2 &{} l_3 \\ k_1 &{} k_2 &{} k_3 \end{pmatrix}&= {\delta _{k_1 + k_2 + k_3, 0}} \frac{(-1)^{l_1 - l_2 -k_3}}{\sqrt{2 l_3 + 1}} s^{l_1,l_2}_{l_3,k_1,k_2}, \end{aligned} \end{aligned}$$

(54)

where the value $s^{l_1,l_2}_{l_3,k_1,k_2}$ is given by

$$\begin{aligned} \begin{aligned}&\sqrt{\frac{ (l_3 + l_1 - l_2)!(l_3 - l_1 + l_2)!(l_1 + l_2 - l_3)!(l_3 - k_3)!(l_3 + k_3)!}{ (l_1 + l_2 +l_3 + 1)!(l_1 - k_1)!(l_1 + k_1)!(l_2 - k_2)!(l_2 + k_2)!}} \\&\times \sum _{t} \frac{(-1)^{t + l_2 + k_2}\sqrt{2l_3+1}(l_3 +l_2 +k_1 -t)!(l_1 -k_1 + t)!}{(l_3 - l_1 + l_2 -t)!(l_3 -k_3 - t)! (t)!(l_1 - l_2 + k_3 + t)!}. \end{aligned} \end{aligned}$$

(55)

The sum over t is chosen such that all variables inside the factorial are non-negative. There are several conditions that make the expression simpler, for example the condition $k_1 = k_2 = k_3 = 0$ which is frequently used in this paper. In this case, Wigner 3j symbols are explicitly given by

$$\begin{aligned} \begin{aligned} \begin{pmatrix} l_1 &{} l_2 &{} l_3 \\ 0 &{} 0 &{} 0 \end{pmatrix}&= (-1)^{L} \Biggl ( \frac{(2L-2l_1)!(2L-2l_2)!(2L-2l_3)!}{(2L+1)!}\Biggr )^{\frac{1}{2}}\\ {}&\Biggl ( \frac{L!}{(L-l_1)!(L-l_2)!(L-l_3)!}\Biggr ), \end{aligned} \end{aligned}$$

(56)

where $2L=l_1+l_2+l_3$ is an even integer.