Directed topological complexity of spheres

Abstract

We show that the directed topological complexity [as defined by Goubault (On directed homotopy equivalences and a notion of directed topological complexity, 2017. arXiv:1709.05702)] of the directed n-sphere is 2, for all $n\ge 1$.

1 Introduction

Topological complexity is a numerical homotopy invariant, defined by Farber (2003, 2004) as part of his topological study of the motion planning problem from robotics. Given a path-connected space X, let PX denote the space of all paths in X endowed with the compact open topology, and let $\pi :PX\rightarrow X\times X$ denote the endpoint fibration given by $\pi (\gamma )=(\gamma (0),\gamma (1))$. Viewing X as the configuration space of some mechanical system, one defines a motion planner on a subset $A\subseteq X\times X$ to be a local section of $\pi$ on A, that is, a continuous map $\sigma : A\rightarrow PX$ such that $\pi \circ \sigma$ equals the inclusion of A into $X\times X$. Assuming X is an Euclidean Neighbourhood Retract (ENR), the topological complexity of X, denoted $\mathsf{TC}(X)$, is defined to be the smallest natural number k such that $X\times X$ admits a partition into k disjoint ENRs, each of which admits a motion planner.

Many basic properties of this invariant were established in the papers (Farber 2003, 2004), which continue to inspire a great deal of research by homotopy theorists [a snapshot of the current state-of-the-art can be found in the conference proceedings volume (Grant et al. 2018)]. Here we simply mention that the topological complexity of spheres was calculated in Farber (2003); it is given by

$$\begin{aligned} \mathsf{TC}(S^n) = {\left\{ \begin{array}{ll} 2 &{} \text{ if } \,n\, \text{ is } \text{ odd, } \\ 3 &{} \text{ if } \,n\, \text{ is } \text{ even. } \end{array}\right. } \end{aligned}$$

In the recent preprint (2017), Goubault defined a variant of topological complexity for directed spaces. Recall that a directed space, or d-space, is a space X together with a distinguished class of paths in X called directed paths, satisfying certain axioms (full definitions will be given in Sect. 2). Partially ordered spaces give examples of d-spaces. The directed paths of a d-space form a subspace $\overrightarrow{P}X$ of PX. The endpoint fibration restricts to a map $\chi :\overrightarrow{P}X\rightarrow X\times X$, which is not surjective in general. Its image, denoted $\Gamma _X\subseteq X\times X$, is the set of $(x,y)\in X\times X$ such that there exists a directed path from x to y. A directed motion planner on a subset $A\subseteq \Gamma _X$ is defined to be a local section of $\chi$ on A. The directed topological complexity of the d-space X, denoted $\overrightarrow{\mathsf{TC}}(X)$, is the smallest natural number k such that $\Gamma _X$ admits a partition into k disjoint ENRs, each of which admits a directed motion planner.

As remarked in the introduction to Goubault (2017), the directed topological complexity seems more suited to studying the motion planning problem in the presence of control constraints on the movements of the various parts of the system. It was shown in Goubault (2017) to be invariant under a suitable notion of directed homotopy equivalence, and a few simple examples were discussed. The article (Goubault et al. 2019) in the present volume provides further examples, and proves several properties of directed topological complexity, including a product formula. It remains to find general upper and lower bounds for this invariant, and to give further computations for familiar d-spaces.

The contribution of this short note is to compute the directed topological complexity of directed spheres. For each $n\ge 1$ the directed sphere $\overrightarrow{S^n}$ is the directed space whose underlying topological space is the boundary $\partial I^{n+1}$ of the $(n+1)$-dimensional unit cube, and whose directed paths are those paths which are non-decreasing in every coordinate.

Theorem

The directed topological complexity of directed spheres is given by

$$\begin{aligned} \overrightarrow{\mathsf{TC}}(\overrightarrow{S^n})=2\quad \text{ for } \text{ all } \,n\ge 1. \end{aligned}$$

This theorem will be proved in Sect. 3 below by exhibiting a partition of $\Gamma _{\overrightarrow{S^n}}$ into 2 disjoint ENRs with explicit motion planners.

2 Preliminaries

Definition 2.1

(Grandis 2003) A directed space or d-space is a pair $(X,\overrightarrow{P}X)$ consisting of a topological space X and a subspace $\overrightarrow{P}X\subseteq PX$ of the path space of X satisfying the following axioms:

• constant paths are in $\overrightarrow{P}X$;

• $\overrightarrow{P}X$ is closed under pre-composition with non-decreasing continuous maps $r:[0,1]\rightarrow [0,1]$;

• $\overrightarrow{P}X$ is closed under concatenation.

The paths in $\overrightarrow{P}X$ are called directed paths or dipaths, and the space $\overrightarrow{P}X$ is called the dipath space.

Examples of d-spaces include partially ordered spaces (where dipaths in $\overrightarrow{P}X$ consist of continuous order-preserving maps $\gamma :([0,1],\le )\rightarrow (X,\le )$) and cubical sets. We can also view any topological space X as a d-space by taking $\overrightarrow{P}X=PX$. The dipath space $\overrightarrow{P}X$ is usually omitted from the notation for a d-space $(X,\overrightarrow{P}X)$.

Definition 2.2

(Goubault 2017) Given a d-space X, let

$$\begin{aligned} \Gamma _X=\{(x,y)\in X\times X\mid \exists \gamma \in \overrightarrow{P}X\, \text{ such } \text{ that } \,\gamma (0)=x,\gamma (1)=y\}\subseteq X\times X. \end{aligned}$$

The dipath space map is given by

$$\begin{aligned} \chi :\overrightarrow{P}X\rightarrow \Gamma _X,\quad \chi (\gamma ) = \big (\gamma (0),\gamma (1)\big ). \end{aligned}$$

That is, the dipath space map is obtained from the classical endpoint fibration $\pi :PX\rightarrow X\times X$ by restriction of domain and codomain.

Definition 2.3

(Goubault 2017) Given a d-space X, its directed topological complexity, denoted $\overrightarrow{\mathsf{TC}}(X)$, is defined to be the smallest natural number k such that there exists a partition $\Gamma _X=A_1\sqcup \cdots \sqcup A_k$ into disjoint ENRs, each of which admits a continuous map $\sigma _i:A_i\rightarrow \overrightarrow{P}X$ such that $\chi \circ \sigma _i = \mathrm{incl}:A_i\hookrightarrow \Gamma _X$.

Remarks 2.4

The dipath space map is not a fibration, in general. One can easily imagine directed spaces X for which the homotopy type of the fibre $\overrightarrow{P}X(x,y)$ is not constant on the path components of $\Gamma _X$. Related to this is the fact that, unlike in the classical case of $\mathsf{TC}(X)$, the above definition does not coincide with the alternative definition using open (or closed) covers. Both of these remarks are due to E. Goubault.

Note that we are using the unreduced version of $\overrightarrow{\mathsf{TC}}$, as in the article (Goubault 2017).

A notion of dihomotopy equivalence was defined in Goubault (2017, Definition 3), and it was shown in Goubault (2017, Lemma 6) that if X and Y are dihomotopy equivalent d-spaces then $\overrightarrow{\mathsf{TC}}(X)=\overrightarrow{\mathsf{TC}}(Y)$. Furthermore, a notion of dicontractibility for d-spaces was outlined in Goubault (2017, Definition 4, Theorem 1) asserts that a d-space X that is contractible in the classical sense has $\overrightarrow{\mathsf{TC}}(X)=1$ if and only if X is dicontractible [see also Goubault et al. (2019, Theorem 1)]. Here we will only require the following weaker assertion. Let us call a d-space $(X,\overrightarrow{P}X)$loop-free if for all $x\in X$, the fibre $\overrightarrow{P}X(x,x)$ consists only of the constant path at x.

Lemma 2.5

Let X be a loop-free d-space for which $\overrightarrow{\mathsf{TC}}(X)=1$. Then for all $(x,y)\in \Gamma _X$, the corresponding fibre $\overrightarrow{P}X(x,y)$ of the dipath space map is contractible.

Proof

We reproduce the relevant part of the proof of Goubault (2017, Theorem 1) (with thanks to the anonymous referees, who pointed out the necessity for an additional assumption such as loop-freeness to ensure continuity of the homotopy below). Suppose $\overrightarrow{\mathsf{TC}}(X)=1$, and let $\sigma :\Gamma _X\rightarrow \overrightarrow{P}X$ be a global section of $\chi :\overrightarrow{P}X\rightarrow \Gamma _X$. Given $(x,y)\in \Gamma _X$, let $f:\{\sigma (x,y)\}\rightarrow \overrightarrow{P}X(x,y)$ and $g:\overrightarrow{P}X(x,y)\rightarrow \{\sigma (x,y)\}$ denote the inclusion and constant maps, respectively. Clearly $g\circ f=\mathrm{Id}_{\{\sigma (x,y)\}}$, so to prove the lemma it suffices to give a homotopy $H:\overrightarrow{P}X(x,y)\times I\rightarrow \overrightarrow{P}X(x,y)$ from $f\circ g$ to $\mathrm{Id}_{\overrightarrow{P}X(x,y)}$. Such a homotopy is defined explicitly by setting

$$\begin{aligned} H(\gamma ,t)(s) = {\left\{ \begin{array}{ll} \gamma (s) &{} \text{ for } \,0\le s\le \frac{t}{2} \\ \sigma \left( \gamma \left( \frac{t}{2}\right) ,\gamma \left( 1-\frac{t}{2}\right) \right) \left( \frac{s-\frac{t}{2}}{1-t}\right) &{} \text{ for } \,\frac{t}{2} \le s \le 1-\frac{t}{2} \\ \gamma (s) &{} \text{ for } \,1-\frac{t}{2} \le s \le 1 \end{array}\right. } \end{aligned}$$

for all $t,s\in [0,1]$. The assumption that X is loop-free ensures that $\sigma (x,x)$ is constant at x for all $x\in X$, which guarantees continuity at $t=1$. $\square$

3 Directed topological complexity of directed spheres

Definition 3.1

Let $n\ge 1$ be a natural number. The directedn-sphere, denoted $\overrightarrow{S^n}$, is the d-space whose underlying space is the boundary $\partial I^{n+1}$ of the unit cube $I^{n+1}=[0,1]^{n+1}\subseteq \mathbb {R}^{n+1}$, and whose dipaths are those paths which are non-decreasing in each coordinate.

We now fix some notation, most of which is borrowed from Fajstrup et al. (2004, Section 6). A point $\mathbf {x}=(x_0,\ldots , x_n)\in \mathbb {R}^{n+1}$ will be denoted $\mathbf {x}=x_0\dots x_n$ for brevity. We use − to denote an arbitrary element of (0, 1). Therefore we may indicate an arbitrary point in $\partial I^{n+1}$ by a string $x_0\dots x_n$ where each $x_i\in \{0,-,1\}$, and at least one $x_i\in \{0,1\}$. We let $[n]=\{0,1,\ldots , n\}$ denote the set which indexes the coordinates.

For example, $--0$ denotes an arbitrary point in the interior of the bottom ($z=0$) face of $\partial I^3$, while $-11$ denotes a point on the interior of the top ($z=1$), back ($y=1$) edge. The point $---$ is not in $\partial I^3$.

With these notations, if $(x_0\dots x_n,y_0\dots y_n)\in \Gamma _{\overrightarrow{S^n}}$ then $x_i\le y_i$ for all $i\in [n]$, but the converse does not hold. For example, any pair of the form $(0--,1--)$ is not in $\Gamma _{\overrightarrow{S^2}}$.

We are now ready to prove our main result, restated here for convenience.

Theorem

The directed topological complexity of directed spheres is given by

$$\begin{aligned} \overrightarrow{\mathsf{TC}}(\overrightarrow{S^n})=2\quad \text{ for } \text{ all } n\ge 1\text{. } \end{aligned}$$

Proof

We first show that $\overrightarrow{\mathsf{TC}}(\overrightarrow{S^n})>1$. Since $\overrightarrow{S^n}$ is loop-free, it suffices by Lemma 2.5 to find $(\mathbf {x},\mathbf {y})\in \Gamma _{\overrightarrow{S^n}}$ such that $\overrightarrow{P}\overrightarrow{S^n}(\mathbf {x},\mathbf {y})$ is not contractible. Fix $x_2,\ldots , x_n\in (0,1)$. It is clear that

$$\begin{aligned} \overrightarrow{P}\overrightarrow{S^n}(00x_2\dots x_n,11x_2\dots x_n)\cong \overrightarrow{P}\overrightarrow{S^1}(00,11), \end{aligned}$$

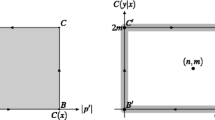
and that the latter space is disconnected (since not all dipaths from 00 to 11 are dihomotopic), see Fig. 1. In particular, $\overrightarrow{P}\overrightarrow{S^n}(00x_2\dots x_n,11x_2\dots x_n)$ is not contractible, hence $\overrightarrow{\mathsf{TC}}(\overrightarrow{S^n})>1$.

Fig. 1

Directed paths in $\overrightarrow{S^2}$ from $00x_2$ to $11x_2$ must remain in the blue square, illustrating the homeomorphism $\overrightarrow{P}\overrightarrow{S^2}(00x_2,11x_2)\cong \overrightarrow{P}\overrightarrow{S^1}(00,11)$

A more direct proof that $\overrightarrow{\mathsf{TC}}(\overrightarrow{S^n})>1$, avoiding the use of Lemma 2.5, may be given as follows. Given $x,t\in (0,1)$, consider points $(\mathbf {x}_1,\mathbf {y}_1)=(t0x\cdots x,11x\cdots x)$ and $(\mathbf {x}_2,\mathbf {y}_2)=(0tx\cdots x,11x\cdots x)$, both in $\Gamma _{\overrightarrow{S^n}}$. A d-path from $\mathbf {x}_1$ to $\mathbf {y}_1$ is contained in the half-square $([0, 1]\times \{0\})\cup (\{1\}\times [0,1])\times \{x\}^{n-1}$, while a d-path from $\mathbf {x}_2$ to $\mathbf {y}_2$ is contained in the half-square $(\{0\}\times [0, 1])\cup ([0,1]\times \{1\})\times \{x\}^{n-1}$ (see Fig. 1 for the case $n = 2$, where the two half-squares are depicted in solid blue and dotted blue respectively). Assuming the existence of a continuous section for the dipath space map on all of $\Gamma _{\overrightarrow{S^n}}$ and letting t tend to 0 results in two disagreeing dipaths from $00x\cdots x$ to $11x\cdots x$, yielding a contradiction. (We are grateful to an anonymous referee for providing this argument.)

To prove that $\overrightarrow{\mathsf{TC}}(\overrightarrow{S^n})\le 2$, we will exhibit a partition $\Gamma _{\overrightarrow{S^n}}=A_1\sqcup A_2$ into two disjoint ENRs, each equipped with a continuous directed motion planner $\sigma _i:A_i\rightarrow \overrightarrow{P}(\overrightarrow{S^n})$.

Consider the d-space $\overrightarrow{\mathbb {R}^{n+1}}$, where the dipaths are non-decreasing in each coordinate. Here we have $\overrightarrow{\mathsf{TC}}(\overrightarrow{\mathbb {R}^{n+1}})=1$, for we can describe a directed motion planner $\widetilde{\sigma _1}$ on

$$\begin{aligned} \Gamma _{\overrightarrow{\mathbb {R}^{n+1}}}=\{(x_0\dots x_n,y_0\dots y_n) \mid x_i\le y_i\quad \text{ for } \text{ all } \,i\in [n]\} \end{aligned}$$

by first increasing $x_0$ to $y_0$, then increasing $x_1$ to $y_1$, and so on, finally increasing $x_n$ to $y_n$. It is not difficult to write a formula for $\widetilde{\sigma _1}$, and check that is it continuous. Similarly, we can define a second motion planner $\widetilde{\sigma _2}$ which first increases $x_n$ to $y_n$, then increases $x_{n-1}$ to $y_{n-1}$, and so on, finally increasing $x_0$ to $y_0$.

For $i=1,2$, let $B_i$ be the set of pairs $(\mathbf {x},\mathbf {y})$ in $\Gamma _{\overrightarrow{S^n}}\subseteq \Gamma _{\overrightarrow{\mathbb {R}^{n+1}}}$ such that the path $\widetilde{\sigma _i}(\mathbf {x},\mathbf {y})$ has image contained in $\partial I^{n+1}$. The restriction $\widetilde{\sigma _i}|_{B_i}:B_i\rightarrow \overrightarrow{P}(\overrightarrow{S^n})$ is clearly continuous, and is a directed motion planner on $B_i$.

We will show that $B_1\cup B_2=\Gamma _{\overrightarrow{S^n}}$, and that both $B_1$ and its complement $U_1:=\Gamma _{\overrightarrow{S^n}}{\setminus } B_1$ are ENRs. Hence we may set $A_1=B_1$ and $A_2=U_1\subseteq B_2$ to obtain a cover by disjoint ENRs with motion planners $\sigma _i=\widetilde{\sigma _i}|_{A_i}$, as required.

The sets $B_1$ and $B_2$ are best understood in terms of their complements $U_1$ and $U_2:=\Gamma _{\overrightarrow{S^n}}{\setminus } B_2$, and in fact we will show that $U_1\cap U_2=\varnothing$.

Observe that $U_1$ is the set of pairs $(\mathbf {x},\mathbf {y})\in \Gamma _{\overrightarrow{S^n}}$ such that $\widetilde{\sigma _1}(\mathbf {x},\mathbf {y})$ enters the interior of the cube, and this can happen upon increasing any of the $n+1$ coordinates. Thus an element $(x_0\dots x_n,y_0\dots y_n)\in U_1$ satisfies the condition:

• $(U_1)$ There exists $j\in [n]$ such that:

  • $x_j<y_j$;

  • $y_i=-$ for all $i\in [n]$ with $i<j$;

  • $x_i=-$ for all $i\in [n]$ with $i>j$.

Similarly, an element $(x_0\dots x_n, y_0\dots y_n)\in U_2$ satisfies the condition:

• $(U_2)$ There exists $k\in [n]$ such that:

  • $x_k<y_k$;

  • $x_i=-$ for all $i\in [n]$ with $i<k$;

  • $y_i=-$ for all $i\in [n]$ with $i>k$.

Now suppose there is an element $(\mathbf {x},\mathbf {y})=(x_0\dots x_n,y_0\dots y_n)\in U_1\cap U_2$.

Then there exist $j,k\in [n]$ such that

$$\begin{aligned} (\mathbf {x},\mathbf {y})&= (x_0\dots x_j-\cdots -,-\cdots - y_j\dots y_n) \\&= (-\cdots - x_k\dots x_n,y_0\dots y_k-\cdots - ). \end{aligned}$$

We observe that if $j<k$ then $\mathbf {x}=-\cdots -$, while if $j>k$ then $\mathbf {y}=-\cdots -$. Both of these give a contradiction, since $\mathbf {x}$ and $\mathbf {y}$ cannot be in the interior of the cube. Hence we must have $j=k$, and $(\mathbf {x},\mathbf {y})=(-\cdots -x_j-\cdots -,-\cdots -y_j-\cdots -)$ where $x_j<y_j$. Since $\mathbf {x}$ and $\mathbf {y}$ are in $\partial I^{n+1}$, we must have $x_j=0<1=y_j$. This gives $(\mathbf {x},\mathbf {y})=(-\cdots - 0-\cdots -,-\cdots - 1 -\cdots -)$ which is not in $\Gamma _{\overrightarrow{S^n}}$, a contradiction.

Thus $U_1\cap U_2=\varnothing$, and $B_1\cup B_2=\Gamma _{\overrightarrow{S^n}}$. It only remains to observe that both $B_1$ and $U_1$ are semi-algebraic subsets of $\mathbb {R}^{2n+2}$ (they are the solution sets of a finite number of linear equalities and inequalities) hence are ENRs. $\square$