Utilization of predictive information to optimize driving and powertrain control of series hybrid vehicles

Abstract

Various publications have demonstrated the utilization of predictive information in optimal control problems of hybrid electric vehicles (HEV) to optimize the energy consumption. Such applications cover the predictive powertrain control and driving strategy for HEV. We introduce in this paper a cooperative controller architecture, so that both optimal controllers interact effectively and exchange predictive information to improve the energy efficiency a step further. Experimental results have confirmed the enhanced fuel economy in comparison to separate operations.

1 Introduction

As a consequence of the regulations on CO₂-emission for new produced cars, as well as the increasing price of crude oil, electric mobility is becoming increasingly attractive for the automotive industry. However, the low energy density of on-board batteries presents pure electric vehicles a challenge of the driving range limitation. Hence, as a compromise, the series hybrid vehicle with a range extender (BEVx) draws a lot of attention from the automotive industry. On the other hand, the technology of intelligent transportation systems, on-board navigation and advanced sensor systems have been developing rapidly. These systems supply the vehicle with look-ahead information such as legal speed limits, traffic information, the road geometry, and topography [9, 10, 14].

Based on that a priori knowledge, it is possible to plan optimal power distribution and/or utilization in terms of efficiency for a finite horizon.

In the case of energy-efficient powertrain control, this various look-ahead information enables us to predict the ego-vehicle speed [13]. Under assumption of this predicted speed profile, we can use a simple driving resistance model to calculate the propulsion force and furthermore power request. Different approaches have been published, discussing how to distribute that work load on the battery and fuel path in the sense of energy efficiency. Those approaches to solve this hereby presented optimal energy management problem include global optimal control (GOC) [1], equivalent consumption minimization strategy [4], and model predictive control (MPC) [2]. MPC has established itself as an attractive approach because of its ability to adapt the optimal control to the instantaneous road information and correct the prediction error. Shen et al. [12] developed a two-scale energy management framework for a range-extender hybrid electric vehicle, in which the controller pre-planned the state of charge (SoC) profile based on the traffic data while MPC used the generated SoC profile for the online optimization. This two-scale framework is extended in this paper through the integration of a predictive driving strategy.

As for the predictive driving strategy, which is represented by model predictive speed and headway control (MPSHC) in this work, the predictive information is used to estimate an allowed speed range for optimization. Then, the optimal solution for driving torque and power generation is calculated to follow the driver’s desired cruising speed as closely as possible. Extensive researches have already been done in energy-efficient speed and headway control (SHC) for either conventional internal-combustion-engine vehicles [6] or battery electric vehicles [11]. Recently, the interest in application of SHC in hybrid electric vehicle (HEV) has been increasing rapidly. Chen et al. [3] considered the control of driving torque and power generation in MPSHC for HEV as a multiple-input and multiple-output (MIMO) system. Since the HEV in his paper is not a plug-in HEV, SoC was assumed constant in the receding horizon of MPC. Moreover, the influence of the road geometry and topography on the speed control range was neglected. In response, a more sophisticated MPC controller will be implemented in this paper.

In spite of the large number of studies in the field of predictive driving strategies and energy-efficient powertrain control strategies, few researchers have done a thorough development and analysis of the cooperative implementation of both strategies, at least for series hybrid vehicles. What this paper mainly contributes is the experimental integration of MPSHC into the two-scale predictive powertrain control. This paper shows the enhanced fuel saving potential through signal exchanges on the MPC level between the two control systems.

2 System configuration

Fig. 1

Structure overview of the vehicular control system concerning the longitudinal dynamics

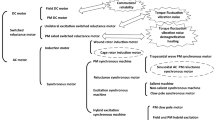
The whole control system of a vehicle concerning the longitudinal dynamics can be generalized as in Fig. 1. Gray blocks are treated as parts of the plant in our control system while the white blocks are the controllers that we discuss in this paper.

On the top level of the vehicle control, the speed and headway control (driving strategy) observes the ego-vehicle as well as the traffic and the road situation. It delivers the acceleration or deceleration demand to the powertrain control. In this paper, MPSHC is activated and takes over the supervisory control task in the longitudinal dynamics from the driver. The powertrain control coordinates the operation load, or more specifically, the output torque of each prime mover (i.e. the engine, and the electric motors), to fulfill the acceleration/deceleration demand. The plant model performs accordingly to the control signals and sends feedbacks including the ego-vehicle speed, the headway to the preceding vehicle, the road information, etc. to the top-level controller.

2.1 Powertrain configuration

The powertrain topology of BEVx is depicted in Fig. 2. The powertrain of a BEVx is a so-called serial hybrid configuration. The generator is mechanically coupled with the internal combustion engine and converts the mechanical power from the engine into electrical power. The generator operates as a motor only when it starts up engine. Its generated electrical power joins the power from the battery to the drive motor. The motor torque drives the wheels through the final drive. The rotational speed of the coupled engine and generator is not linked to the vehicle speed, or in other words, is not determined by the vehicle speed. In that way, we bundle the engine and the generator into a so-called auxiliary power unit (APU) in our discussion. The connection between APU and other parts of the powertrain is derived from the electrical power balance. This consideration leads to separating the control of APU’s operation from the energy management (see Fig. 3).

Fig. 2

BEVx powertrain topology

Fig. 3

Flowchart of the combined control architecture

2.2 Controller architecture

The controller architecture of the combined driving strategy and powertrain control is basically a two-scale framework and is depicted in Fig. 3. The offline blocks are in gray and the online blocks are in white. The upper level, which is at the meantime applied offline, consists of speed prediction and SoC planning. The road information such as road geometry and legal speed limits is utilized to predict the speed profile over the whole mission. Using this a priori knowledge, an optimal SoC profile can be planned by solving a global optimal control problem (OCP). The SoC profile is saved as a look-up table (LUT) in reference to distance ${s}$. The lower level is executed online repeatedly in each receding horizon. MPSHC is employed to optimize the future driving speed within the horizon. As declared in Sect. 2.1, APU control is separated from the energy management. Thus, the powertrain control is divided into MPC energy management and APU control. Note that MPSHC we apply in our paper can yield the traction torque demand directly and pass it on to the plant.

It is to be noted that the actual vehicle speed ${v}$ might deviate from the generated $\overline{v}(s)$ and also the offline predicted $v_\mathrm {pred}$. That prediction inaccuracy results in errors in the planned SoC reference trajectory. In the receding horizon, the planned SoC reference is taken over as the terminal SoC constraint. Because of the feedback loop of MPC, re-estimating the control variables can compensate for the error in SoC planning as well as in speed prediction.

The procedure of the control system goes as follows:

• 1. Obtain the route information of the mission and predict the speed profile. Use it to calculate the optimal SoC trajectory and save it up in LUT with the distance ${s}$ as reference.

• 2. By observation of the road and traffic (including the headway to the preceding vehicle) as well as the ego-vehicle speed, predict the future speed of the preceding vehicle and estimate the permissible speed range of the ego-vehicle for the following optimization.

• 3. Given the SoC reference and the permissible speed range ($\overline{v}_\mathrm {max}(s)$ and $\overline{v}_\mathrm {min}(s)$), MPSHC calculates the optimal control policy for the drive torque $T_\mathrm {mot}$. Meanwhile, an optimal speed trajectory within the horizon is generated.

• 4. Using the same SoC reference and generated speed trajectory, the MPC energy management calculates the optimal power generation from APU.

• 5. Provided the power demand $P_\mathrm {apu}$, APU control coordinates the engine and the motor to stay on the optimal operation line (OOL) of APU to ensure best efficiency.

• 6. Carry out the first step in the sequence of the optimal control policy for the driving torque $T_\mathrm {mot}$, and APU dynamics control $T_\mathrm {eng}$ and $T_\mathrm {gen}$.

• 7. The simulated plant model gives feedback of the vehicle speed ${v}$, the traveled distance ${s}$, the battery SoC, and the rotational speed of APU $\omega _\mathrm {apu}$.

Among all those steps, step 2 to 5 occur in the receding horizon level. Step 1 is activated only before the mission starts whereas the other steps run online in a loop.

In comparison to the two-scale energy management framework proposed in [12], the estimation of the online speed trajectory in the receding horizon $\overline{v}(s)$ is no more based on a pure prediction of future driver reactions, but instead on the optimized speed planning by MPSHC. That should lead to a better optimization quality compared to the case of pure anticipation. On the other hand, if we compare the approach in this paper with an ordinary MPSHC, it is obvious that the optimization on power distribution/generation is enhanced. In strict definition, MPSHC for hybrid vehicles is classified as a MIMO-system. To achieve a faster calculation, the control-oriented control concerning power generation is usually much simplified. The separated powertrain control can utilize a more detailed model for power generation optimization without adding complexity to MPSHC. Therefore, the real-time capability will not be damaged.

3 SoC reference generation

For means of simulation, the route information is provided in form of a list of three-dimensional Cartesian coordinates of the road knots. The speed limit signs, i.e. the positions and the values of the speed limits, are saved in a data bank. The information is then forwarded to the offline speed prediction block.

3.1 Offline speed prediction

The objective of this block is to approximately calculate the speed profile of the whole driving mission, based on the speed limits and the driver’s lateral acceleration limit. We characterize the driver with parameters such as the maximal and minimal longitudinal acceleration, the maximal lateral acceleration, and the preferred cruising speed.

Out of the x–y coordinate sequence, the curvature over distance $\kappa (s)$ can be easily deduced. Together with the speed limitation that results from the driver’s maximal bearable lateral acceleration in curves $a_\mathrm {y,max}$,

$$\begin{aligned} v_\mathrm {c,max}(s) = \sqrt{a_\mathrm {y,max} / \left| \kappa (s)\right| }, \end{aligned}$$

(1)

we can determine the maximal cornering speed over distance $v_\mathrm {c,max}(s)$. Combined with the legal speed limit $v_\mathrm {lim}(s)$ and driver’s desired cruising speed, we are able to estimate the maximal permissible speed outline over distance $v_\mathrm {max}(s).$ By taking the longitudinal maximal acceleration and deceleration into account, we achieve the final predicted speed trajectory over distance $v_\mathrm {pred}(s)$.

3.2 Optimal SoC planning

The optimal problem can be described mathematically as follows:

$$\begin{aligned} \min _{P_\mathrm {apu}(\cdot )} \qquad&J_\mathrm {pt} = \int _{t_0}^{t_\mathrm {f}}\! \dot{m}_\mathrm {f}(P_\mathrm {apu}(t))\, \mathrm {d}t \end{aligned}$$

(2a)

subject to

$$\begin{aligned}&\dot{\mathrm{SoC}} = f(\mathrm{SoC}, P_\mathrm {apu}, P_\mathrm {mot,e},t) \end{aligned}$$

(2b)

$$\begin{aligned}&\mathrm{SoC}(t_0) = \mathrm{SoC}_0\end{aligned}$$

(2c)

$$\begin{aligned}&P_\mathrm {apu,min} \le P_\mathrm {apu} \le P_\mathrm {apu,max}\end{aligned}$$

(2d)

$$\begin{aligned}&\mathrm{SoC}_\mathrm {min}\le \mathrm{SoC} \le \mathrm{SoC}_\mathrm {max}, \end{aligned}$$

(2e)

where $\dot{m}_\mathrm {f}$ is the fuel mass flow rate in kg/s as a function of the control variable, which is the electric power $P_\mathrm {apu}$ delivered by APU. $P_\text{mot,e}$ denotes the electrical power on the traction motor, which should be regarded as the disturbance to the battery dynamics (2b). At the beginning of the trip $t=t_0$, SoC starts at the initial state $\mathrm{SoC}_0$. Note that the terminal state constraint at $t=t_\mathrm {f}$ does not exist in offline GOC. That is because SoC is not required to be held at a certain level to ensure the sustainability for hybrid functionality, as in the case of HEV without Plug-in.

Obviously, there are still the fuel consumption model $\dot{m}_\mathrm {f}(P_\mathrm {apu})$, the system dynamics $f(\mathrm{SoC}, P_\mathrm {apu}, P_\mathrm {mot,e},t)$, and the disturbance sequence $P_\mathrm {mot,e}(t)$ in the problem description (2) left to be defined.

3.2.1 Fuel consumption rate $\dot{m}_\mathrm {f}(P_\mathrm {apu})$

The concept OOL is widely applied to achieve the optimal efficiency of APU. It is composed of operating points (pairs of rotational speed and torque) that maximize the efficiency for each value of output power. It defines a certain relationship between the output power and the operating point, which is further associated with the fuel consumption rate. Under the assumption that APU operates strictly along OOL and the influence of the APU dynamics on consumption is neglected, then the fuel consumption rate can be expressed as a function of the output power $P_\mathrm {apu}$.

3.2.2 Battery SoC dynamics $f(\cdot )$

Battery SoC is the only state variable in an HEV energy management problem and its variation is influenced by its output power $P_\mathrm {bat}$:

$$\begin{aligned}&\dot{\mathrm{SoC}}= c_\mathrm {bat1} \left( {V_\mathrm {oc} - \sqrt{V_\mathrm {oc}^2 - c_\mathrm {bat2} P_\mathrm {bat}(t)} } \right)&\end{aligned}$$

(3a)

$$\begin{aligned} \text {with }\qquad&c_\mathrm {bat1}= -\left( 2\,Q_\mathrm {bat} R_\mathrm {bat} \right) ^{-1}, \quad c_\mathrm {bat2} = 4\,R_\mathrm {bat},&\end{aligned}$$

(3b)

where $V_\mathrm {oc}$ is the open-circuit voltage of the battery, $Q_\mathrm {bat}$ the full electric charge and $R_\mathrm {bat}$ the internal resistance of the battery. The battery power is linked with the electrical power of the motor $P_\mathrm {mot,e}$ and APU $P_\mathrm {apu}$, which correspond to the system disturbance and the control respectively:

$$\begin{aligned} P_\mathrm {bat} = P_\mathrm {mot,e}-P_\mathrm {apu}. \end{aligned}$$

(4)

By substitution of $P_\mathrm {bat}$ in (3a), it yields the system dynamics explicitly dependent of the disturbance and the control ($P_\mathrm {mot,e}$ and $P_\mathrm {apu}$):

$$\begin{aligned} \dot{\mathrm{SoC}} = c_\mathrm {bat1} \left( {V_\mathrm {oc} - \sqrt{V_\mathrm {oc}^2 + c_\mathrm {bat2} (P_\mathrm {apu}-P_\mathrm {mot,e})} }\right) . \end{aligned}$$

(5)

3.2.3 Disturbance sequence $P_\mathrm {mot,e}(t)$

The disturbance to the system is the total electrical power for propulsion, which is in this case exactly the electrical power of the motor $P_\mathrm {mot,e}$. $P_\mathrm {mot,e}$ can be deduced from the speed ${v}$ and the torques at the wheels $T_\mathrm {mot}$. They are yielded by the knowledge of the predicted speed profile. Using the driving resistance model, the driving torque at the motor $T_\mathrm {mot}$ traces back to the inertia forces, the aerodynamic friction, the rolling resistance, and the uphill driving force [see ref. 10]:

$$\begin{aligned} T_\mathrm {mot} = \frac{r_\mathrm {w}}{\gamma } \bigg ( (m_\mathrm {v} + m_\mathrm {r}) \, \dot{v} + \frac{1}{2} \,\rho _\mathrm {a} \,A_\mathrm {f} \,c_\mathrm {d} \,v^2 + c_\mathrm {r}\, m_\mathrm {v} \,g \,\cos (\alpha ) + m_\mathrm {v} \,g \,\sin (\alpha ) \bigg ), \end{aligned}$$

(6)

while the rotational speed of the motor $\omega _\mathrm {mot}$ derives from the vehicle speed ${v}$:

$$\begin{aligned} \omega _\mathrm {mot} = \frac{\gamma }{r_\mathrm {w}} \, v. \end{aligned}$$

(7)

Here $r_\mathrm {w}$ denotes the wheel radius and $\gamma$ the total transmission ratio. $m_\mathrm {v}$ and $m_\mathrm {r}$ denotes the vehicle mass and the equivalent mass of rotating parts respectively (Definition see [5], p.17). $\rho _\mathrm {a}$, $\,A_\mathrm {f}$, and $c_\mathrm {d}$ are the air density, the vehicle frontal area, and the air drag coefficient. $c_\mathrm {r}$, ${g}$, and $\alpha$ represent the tire roll resistance coefficient, the gravity, and the road slope angle.

Considering the conversion efficiency $\eta _\mathrm {mot}$, the disturbance, i.e. the motor electrical power is estimated as follows:

$$\begin{aligned} P_\mathrm {mot,e} = T_\mathrm {mot} \, \omega _\mathrm {mot} \ \eta _\mathrm {mot}^{{\text {sign}}(-T_\mathrm {mot} \, \omega _\mathrm {mot})}, \end{aligned}$$

(8)

where $\eta _\mathrm {mot}$ is a function of $T_\mathrm {mot}$ and $\omega _\mathrm {mot}$.

Now that the whole nonlinear OCP is defined, we can apply Pontryagin’s Minimum Principle (PMP) to solve the problem. In the previous work [12], the authors already explained the solution using PMP. This paper, therefore, does not pursue the solving process further. All in all, we acquire an optimal SoC reference over travel time $\mathrm{SoC}_\mathrm {pred}(t)$. With the predicted speed profile in Sect. 3.1, the SoC reference trajectory can be mapped onto the travel distance and it yields $\mathrm{SoC}_\mathrm {pred}(s)$.

4 Driving strategy

MPSHC concerns solving OCP in each distance horizon, where the control-oriented system model consists of battery dynamics and vehicular longitudinal dynamics. The state variables ($\mathrm{SoC}$ and ${v}$) in the system are constrained. While the constraint for SoC is quite trivial to determine, the speed constraint must be estimated based on the road and traffic information. Therefore, the route information is once again put into service. This predictive information is conveyed to the block Sect. 4.1 (see Fig. 3). Note that the distance regarding the horizon is denoted as $\sigma \in [0, s_\mathrm {hrz}]$, while ${s}$ is used for the distance in the whole mission scale. $s_\mathrm {hrz}$ is the horizon length.

4.1 Horizon speed restriction

Just as its name tells, MPSHC has two tasks: headway and speed control. It is necessary to discuss how to specify the speed constraint for each case separately. The introduced approach derives from [6]. Note that the calculation of the speed bounds takes place once at the beginning of each receding horizon.

4.1.1 Speed constraint during speed control

Speed control occurs when the road way ahead of the ego-vehicle is free of traffic. The simplest case would be driving on a road without speed limits. We assume that the driver has chosen the set speed $v_\mathrm {set}$. Then the upper and lower bound of the speed, $\overline{v}_\mathrm {max}$ and $\overline{v}_\mathrm {min}$, can be determined by a coefficient $c_\mathrm {vset}$:

$$\begin{aligned} \overline{v}_\mathrm {max} = (1 + c_\mathrm {vset})\, v_\mathrm {set}, \quad \overline{v}_\mathrm {min} = (1 - c_\mathrm {vset}) \, v_\mathrm {set}. \end{aligned}$$

(9)

If the speed limit lower than $\overline{v}_\mathrm {max}$ is detected, the speed bounds resulting from (9) are overridden. Figure 4 explains the adaption. The gradient of the envelope is predefined by a parameter. The tunable weighting factor $c_\mathrm {vref}$ defines the reference speed:

$$\begin{aligned} \overline{v}_\mathrm {ref}(\sigma ) = \overline{v}_\mathrm {max}(\sigma ) - c_\mathrm {vref} \big ( \overline{v}_\mathrm {max}(\sigma ) - \overline{v}_\mathrm {min}(\sigma ) \big ), \end{aligned}$$

(10)

where the value of $c_\mathrm {vref}$ is looked up from a table with reference to the difference of $\overline{v}_\mathrm {max}$ and $v_\mathrm {set}$. As Fig. 4a shows, this weighting factor drags the reference speed close to the upper bound.

Fig. 4

Speed envelope during a speed and b headway control

4.1.2 Speed constraint during headway control

If there is a preceding vehicle running within the radar range, the speed envelope is then developed based on the distance ahead and the speed of the object vehicle in front $v_\mathrm {obj}$. The starting point is to plan a reference speed trajectory $\overline{v}_\mathrm {ref}(\sigma )$ within the horizon. Under the assumption that the preceding vehicle remains at the speed $v_\mathrm {obj}$ from the beginning till the end of the horizon [6], introduced a method to generate the trajectory and it can be expressed as a modified exponential function of time:

$$\begin{aligned} \overline{v}_\mathrm {ref} = v_\mathrm {obj} + \left( \overline{v}_\mathrm {0}-v_\mathrm {obj} \right) \, {\text {e}}^{-c_\mathrm {trj}t + c_\mathrm {trj,0}}, \end{aligned}$$

(11)

where the gradient $c_\mathrm {trj}$ influences the swiftness of $\overline{v}_\mathrm {ref}$ approaching $v_\mathrm {obj}$ and the constant $c_\mathrm {trj,0}$ reflects the initial headway and speed difference at the beginning of the horizon. $\overline{v}_\mathrm {0}$ denotes the ego-vehicle speed at the horizon start. The deduced trajectory is subsequently cast onto the distance axis, and is depicted in Fig. 4b. Using (9), the speed envelope can be derived from the reference speed trajectory $\overline{v}_\mathrm {ref}$ in the same way.

4.2 Model predictive speed and headway control

Different than in the powertrain control, the optimal trajectories are planned along the traveled distance $\sigma$. Within the horizon, it applies: $\sigma \in [0, s_\mathrm {hrz}]$. Inside the MPSHC block, the control vector $\varvec{u}$ is composed of the drive torque of the traction motor $T_\mathrm {mot}$ and the electric power $P_\mathrm {bat}$ delivered by the battery,

$$\begin{aligned} \varvec{u} = [T_\mathrm {mot} ~ P_\mathrm {bat}]^\top . \end{aligned}$$

(12)

The state vector $\varvec{x}$ comprises the ego-vehicle speed ${v}$ and the battery SoC,

$$\begin{aligned} \varvec{x} = [v^2 \ \mathrm{SoC}]^\top . \end{aligned}$$

(13)

The OCP in a single horizon can be formulated as follows,

$$\begin{aligned} \min _{\varvec{u}(\cdot )} \qquad J_\mathrm {sh} &= \int _{0}^{s_\mathrm {hrz}}\! \dot{m}_\mathrm {f}^2(\varvec{u}) + \beta P_\mathrm {mot,e}^2(u_1) \ \mathrm {d}\sigma \end{aligned}$$

(14a)

subject to

$$\begin{aligned}\frac{\mathrm {d}\varvec{x}}{\mathrm {d}\sigma } &= \varvec{f}(\varvec{x}, \varvec{u}, d, \sigma ) \end{aligned}$$

(14b)

$$\begin{aligned} \varvec{x}(0) &= \varvec{x}_0\end{aligned}$$

(14c)

$$\begin{aligned}&x_\mathrm {1,min} \le x_1 \le x_\mathrm {1,max}\end{aligned}$$

(14d)

$$\begin{aligned}&x_2(s_\mathrm {hrz}) \ge \mathrm{SoC}_\mathrm {pred}(s+s_\mathrm {hrz})\end{aligned}$$

(14e)

$$\begin{aligned}&\varvec{u}_\mathrm {min}\le \varvec{u} \le \varvec{u}_\mathrm {max}. \end{aligned}$$

(14f)

The fuel mass flow rate $\dot{m}_\mathrm {f}$ in kg/s is a function of the control vector $\varvec{u}$. The disturbance ${d}$ is the road slope grade $\alpha$ which is calculated from the topography. At the beginning of the horizon, $\varvec{x}$ start with $\varvec{x}_0$. It is shown in Sect. 4.1.1 how the constraints for the first state $x_1$ are defined. The terminal constraint for the second state $x_2$ comes from the generated SoC reference trajectory shown in Sect. 3.2. The constraints for both control variables are, however, determined by the components’ physical properties.

The functions $\dot{m}_\mathrm {f}(\varvec{u})$, $P_\mathrm {mot,e}(u_1)$ and $\varvec{f}(\varvec{x},\varvec{u}, d, \sigma )$ are explained in the following subsections.

4.3 Cost function $J_\mathrm {sh}$

The cost function used to optimize both the fuel consumption of the APU and the electric energy consumption of the traction motor is defined in (14a), where $\beta$ weights the usage of electrical energy against the consumption of fuel energy. In the cost function, $\dot{m}_\mathrm {f}$ in the first term can be expressed as follows,

$$\begin{aligned} \dot{m}_\mathrm {f}(\varvec{u}) = c_\mathrm {fuel1} \big ( P_\mathrm {mot,e}(u_1) - u_2 \big ) + c_\mathrm {fuel0}, \end{aligned}$$

(15)

in which OOL is approximated as a straight line with the coefficient $c_\mathrm {fuel1}$ and the constant $c_\mathrm {fuel0}$. Here $P_\mathrm {mot,e}$ is dependent on $u_1$. For each $\omega _\mathrm {mot}$, $P_\mathrm {mot,e}$ can be fitted with a linear function of $u_1 := T_\mathrm {mot}$,

$$\begin{aligned} P_\mathrm {mot,e}(u_1) = (c_\mathrm {mot1}\,u_1 + c_\mathrm {mot0}) \, \omega _\mathrm {mot}. \end{aligned}$$

(16)

Both quadratics inside the integral in the cost function (14a) are used to avoid the chattering in the optimal solution, which is caused by the linear programming.

4.4 System dynamics ${f}(\cdot )$

Corresponding to the elements in state vectors, the system dynamics consists of two ordinary differential equations. The first differential equation is derived from the driving resistance model (6), and can be expressed as follows,

$$\begin{aligned} \frac{\mathrm {d}x_1}{\mathrm {d}\sigma } = \left( - \frac{1}{2}\rho _\mathrm {a}A_\mathrm {f}c_\mathrm {d}\, x_1 + \frac{\gamma }{r_\mathrm {w}} \, u_1- c_\mathrm {r}m_\mathrm {v}g\cos (\alpha ) + m_\mathrm {v}g\sin (\alpha ) \right) \bigg / \left( \frac{1}{2}\left( m_\mathrm {v} + m_\mathrm {r} \right) \right) , \end{aligned}$$

(17)

in which the parameters are declared as same as in (6) and (7). The second dynamic equation is the battery dynamics.

In contrast to energy management, driving strategy is more concerned about optimizing speed trajectories rather than minimizing the losses in powertrain. Besides, the battery is characterized with a quite high efficiency, over $92{\%}$ for Li-ion batteries in rated operation ranges [7]. Hence, to keep the problem necessarily simple, we neglect the internal resistance and thus obtain the equation,

$$\begin{aligned} \frac{\mathrm {d}x_2}{\mathrm {d}\sigma } = \frac{u_2}{Q_\mathrm {bat} V_\mathrm {oc} \, v}. \end{aligned}$$

(18)

The fully defined MPSHC problem is solved using a numeric toolbox MOSEK choosing the interior-point method [see Ref. 9]. As results, we obtain for each horizon the optimal trajectories of $\overline{v}(\sigma )$ and $T_\mathrm {mot}(\sigma )$. The sequence $\overline{v}(\sigma )$ is forwarded to the powertrain control.

5 Predictive powertrain control

Since the powertrain control applies the time axis as reference, it is necessary to convert the predictive speed information over distance $\overline{v}(\sigma )$ from MPSHC onto the time axis and we acquire $\overline{v}(t)$. Based on that, we can calculate the travel distance at each horizon end $\overline{s}(t_\mathrm {f})$. The SoC set-point at the horizon end derives with reference to the offline SoC plan: $\mathrm{SoC}_\mathrm {pred}(\overline{s}(t_\mathrm {f}))$.

5.1 Model predictive energy management

Model predictive energy management solves one OCP with $\tau \in [0, t_\mathrm {hrz}]$ in every receding horizon with the horizon length $t_\mathrm {hrz}$. In our case, OCP in MPC level is exactly the same as in the offline planning level (see Sect. 3.2) except for the initial and final state boundary conditions:

$$\begin{aligned} \mathrm{SoC}(\tau = 0) = \mathrm{SoC}(t), \quad \mathrm{SoC}(\tau = t_\mathrm {hrz}) = \mathrm{SoC}_\mathrm {pred}(t+t_\mathrm {hrz}), \end{aligned}$$

(19)

in which $\mathrm{SoC}(t)$ means the measured SoC at the moment, while $\mathrm{SoC}_\mathrm {pred}(t+t_\mathrm {hrz})$ is looked up in the SoC trajectory planned by GOC (see Sect. 3.2). Note that MPSHC provides more accurate prediction on speed than the offline prediction. Therefore, the speed plan $\overline{v}(\sigma )$ from MPSHC is applied for estimating the system disturbance ${d}$ (see Sect. 3.2.3). OCP in this level is also solved with an algorithm based on PMP.

5.2 APU control

The task of APU control is to supply the engine and the motor with torque commands so that their rotational speeds follow OOL. Corresponding to every power demand $P_\mathrm {gen},$ a desired value of rotational speed can be interpreted. A simple PID controller is used here to minimize the rotational speed error by controlling the combined torque ${\Sigma } T_\mathrm {apu} = T_\mathrm {gen}-T_\mathrm {eng}$. One degree of freedom in dividing the torque to the engine and the generator is eliminated, when the engine set-point torque is set to the correspondent value on OOL and the rest of the desired torque is provided by the generator.

6 Simulation results

The control strategy is realized in Matlab/Simulink. It is then tested in a combined simulation environment of TUBCarDynamics and IPG CarMaker. The former is developed by the institute to simulate the vehicle dynamics. The latter is a commercial vehicle simulation environment and has a detailed and realistic modeling of the powertrain dynamics.

We have chosen a 7840 m long road for test as depicted in Fig. 5a. The set speed $v_\mathrm {set}$ is chosen at 75 km/h. At 1000 m a heading vehicle cuts in and swings out at 5000 m, moving at a varying speed (see Fig. 5b). To evaluate the fuel saving caused by the driving strategy and by the powertrain control separately, three strategies with different integration degrees of predictive controls have been tested (see Table 1).

Fig. 5

Test route overview. a x–y Coordinates of the route. b In above, the speed profiles over distance of the speed limits $v_\mathrm {lim}$ and the preceding object vehicle $v_\mathrm {obj}$; in below, the elevation profile over distance $h(s)$

Table 1 Combined strategies of different driving and powertrain controls

The first is a conventional adaptive cruise control (ACC) combined with a simple charge-depleting charge-sustaining (CDCS) strategy. The second is enhanced by MPSHC, whereas the powertrain control remains the same. The last is the proposed combined strategy in this paper.

Table 2 shows the relative comparison of fuel and electric energy consumption as well as the travel time one against another. The progressive fuel saving improvement shown in Table 2 has confirmed the anticipation that benefits of predictive information from the driving and the powertrain control levels, respectively, can be accumulated. From Fig. 6 we can infer that the fuel saving caused by the predictive powertrain control leads back to two facts. First, the offline global SoC planning prevents SoC from reaching the lower boundary in an early phase. It enables the APU to select the operation point with an overview on the whole trip instead of based on the current power demand or a limited preview. Second, the online predictive powertrain control takes advantage of the first aspect to have the APU work at the most efficient points mostly.

Table 2 Comparison of the combined strategies

Fig. 6

Simulation result of SoC, vehicle speed ${v}$, electric power of the drive motor $P_\mathrm {mot,e}$, and output power of APU $P_\mathrm {apu}$

It is difficult to infer the reason for the fuel saving caused by the predictive driving strategy directly from Fig. 6. Therefore, two route segments have been chosen to be observed closely. In the first case in Fig. 7a, the large deceleration is caused by the occurrence of two low-speed limits at around 6900 m. It is obvious that the predictive driving strategy (strategy 2 and 3) makes the vehicle decelerate earlier than that with ACC (strategy 1). Much less torques are employed in deceleration. As a result, the speed trajectories turn out smoother than with ACC. Knowing that the vehicle has to decelerate soon, the predictive driving strategy chose a little higher torque of a higher efficiency for a short distance, instead of keeping the speed constant with a torque of lower efficiency. The kinetic energy reserve was paid off during the following smooth deceleration.

Fig. 7

Results in two road segments: a speed limit occurs and b vehicle runs in front

The second case is the traffic scenario with a vehicle running in front. The object vehicle speed is depicted in red in Fig. 7b. At the beginning, the object vehicle is detected by the radar. It first decelerates and then accelerates. The ego-vehicle performs correspondingly. In the case of ACC, the ego-vehicle keeps the same speed until the set distance is almost reached. Then it decelerates sharply until a safe headway can be held. As for the predictive driving strategy, the ego-vehicle starts to decelerate already at the beginning of the scenario. The early deceleration enables the ego-vehicle to brake more tenderly. A comparable behavior can be found during the acceleration. No matter in which case the less brake and driving torque brings about energy saving.

7 Conclusion

This paper introduces a solution for two controllers of different architecture levels to work together. It shows the combined controller structure brings benefits for both strategies/controllers because of more detailed and comprehensive predictive information. That enhancement leads to a great improvement in accuracy of the a priori knowledge, which is the basis for the optimization calculation inside each predictive controller. In the future, we plan to include other information in offline SoC planning, e.g., traffic flow, traffic light signals, etc. Other than that, further investigations will be undertaken for the influence of the test scenario, as well as vehicle configuration on the fuel saving potential.