1 Introduction

With the increase in complexity of spacecraft missions, complex spacecraft with multiple components have become an important development direction in space engineering, which has promoted the attitude control of complex spacecraft to become a research field of interest. The structure and mission complexity of spacecraft have increased, and the probability of actuator failure has also increased when operating in a complex and changeable space environment. The performance of spacecraft attitude control depends on the system hardware facilities and the on-board attitude control algorithm. According to statistics, the failure of the spacecraft attitude control system causes approximately 40\(\%\) of satellite failures, and actuator failure accounts for approximately one-third of spacecraft attitude control system failures [1]. In addition, the control algorithms commonly used in actual engineering have poor adaptability to the problems of spacecraft model uncertainty, imbalance, external disturbance, and actuator failure. In recent years, spacecraft attitude control algorithms such as adaptive control [2], neural networks [3], robust control [4, 5], optimal control, sliding mode control [6], fuzzy logic [7] and intelligent control [8,9,10] have gradually attracted attention.

In recent years, finite-time controllers have been widely used in spacecraft attitude control, and they have strong robustness [11,12,13]. The adaptive algorithm has strong anti-interference ability and good reliability. Combining this with other control algorithms has a faster response speed and higher steady-state accuracy [14, 15]. Associative control algorithms are increasingly being used in spacecraft attitude control for actuator failures. Hu et al.  [16] designed an adaptive backstepping control strategy to achieve stable attitude in the case of external disturbance and actuator failure, and it was proved that the law can effectively realize robustness and high-precision stability of fault-tolerant control. Gui et al. [17] designed a new integral terminal sliding mode controller to consider the attitude tracking of rigid spacecraft in the presence of uncertain inertia, unknown interference and sudden actuator failure, and proved its superiority performance. Li et al. [18] designed a robust fault-tolerant state of multi-boundary dependence for unknown disturbances and actuator faults when the flexible spacecraft is in orbit. The controller can ensure that the closed-loop system is asymptotically stable and satisfies its flexibility and conservativeness. Chen et al. [19] proposed a robust fault-tolerant control design method based on the linear matrix inequality (LMI) method; however, the redundant installation or failure of the actuator has not been considered. To solve the problem of actuator failure, Jiang et al. [20] proposed an adaptive attitude controller using a redundancy actuator control strategy to achieve high precision of the attitude, but the failure processing method can still be improved. Liu et al. [21] proposed an adaptive fuzzy backstepping control scheme to solve the fault-tolerant attitude control of flexible spacecraft under the digital communication channel through sensor signals and controller indicators. This strategy can guarantee the superiority and effectiveness of the spacecraft system in the presence of inertial uncertainty, external interference, actuator saturation, and other faults. Gao et al. [22] proposed a method that combines fuzzy logic and sliding mode control to study the attitude-tracking control of a rigid spacecraft. However, the control scheme for complex spacecraft should still be studied. Wang et al. [23] proposed an ISM-based nonsmooth controller with finite-time auxiliary compensation dynamics to realize exact fault-tolerance and unknown rejection, the remarkable performance was also demonstrated by the simulation results and comparisons. Furthermore, Fixed-time control can be used to obtain the required finite-time convergence without considering any initial conditions. This is one of the most commonly used spacecraft attitude-control methods. In reference [24], a fixed-time control scheme was proposed to ensure that the system converged in a fixed time, despite the system uncertainty and unknown interference. The fixed-time attitude-tracking problem of a rigid spacecraft was studied. The fixed-time controller can predefine the convergence rate of the system state offline [25,26,27]. In this case, the closed-loop stabilization time is independent of the initial state and can be estimated in advance.

Based on the aforementioned studies, this study conducts research on flexible spacecraft with rotating appendages and platforms, while considering the influence of the rotation and vibration of flexible solar panels and the influence of rigid rotating payload. The main purpose of this paper is to solve the attitude control problem of this kind of complex spacecraft, and realize the earth observation under the stable rotation of the spacecraft appendages, the attitude dynamics and kinematics equations of the flexible spacecraft with rotating appendages are established, and an adaptive fuzzy logic scheme that combines finite-time sliding mode control is designed for the spacecraft platform, as well as a fixed-time controller for the rotating appendages. These strategies can effectively achieve fast and stable effects in the second and third parts.Then the numerical simulation analysis can prove the stability and robustness of the spacecraft even with the actuator fault. Finally, the corresponding conclusions illustrate the effectiveness of the designed control strategies.

2 Problem Formulation

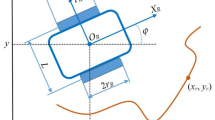
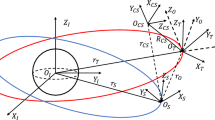
In this paper, the spacecraft platform carries rotating rigid parts and flexible solar panels. The complex spacecraft system has strong nonlinearity and is susceptible to external interference and rotating appendages. As shown in Fig. 1, the spacecraft consists of a platform, rotating flexible solar panels and a rotating payload.

Fig. 1
figure 1

The structure of spacecraft system

Full size image

To avoid singularity, unit quaternions are often used to describe the kinematics of a spacecraft. A unit quaternion can be expressed as \({\varvec{q}} = {\left[ {{q_0},{\varvec{q}}_v^{\text{T}}} \right] ^{\text{T}}} = {\left[ {{q_0},{q_1},{q_2},{q_3}} \right] ^{\text{T}}}\),where \({q_0}\) is the scalar part of the quaternion, and \({{\varvec{q}}_v}\) is the vector part of the quaternion, satisfying the condition \(q_0^2 + q_v^{\text{T}}{q_v} = 1\). The kinematic equation for the quaternion of the spacecraft can be given as:

$$\begin{aligned} \text{d}{\varvec{q}} = \frac{1}{2}{\varvec{Q}}\left( {\varvec{q}} \right) * {\varvec{\omega }} \end{aligned}$$
(1)

where \({\varvec{Q}}({\varvec{q}}) = \left[ { - {\varvec{q}}_v^{\text{T}};{q_0}{\varvec{I}} + {\varvec{q}}_v^ \times } \right]\),\({\varvec{\omega }}\) denotes the angular attitude velocity of the spacecraft relative to the centre of the platform, and \({\varvec{q}}_v^ \times\) represents the skew symmetric matrix of \({{\varvec{q}}_v}\) such that \({\varvec{q}}_v^ \times = \left[ {0, - {q_3},{q_2};} \right.\) \(\left. {{q_3},0, - {q_1}; - {q_2},{q_1},0} \right]\). Considering the rigid-flexible coupling spacecraft carrying the rotation rigid components and flexible solar panels, we considered. Considering the translation and rotation of the spacecraft system and the modal vibration of the solar panels, the Lagrange method was applied to derive the complex dynamic model equations of the spacecraft system. The equation for the spacecraft platform is as follows:

$$\begin{aligned} {{{{\textbf{I}}}_b}{{{\dot{\varvec{\omega }}}}_b} + {{{{\varvec{\tilde \omega }}}}_b}({{\varvec{\mathrm{I}}}_b}{{\varvec{\omega }}_b} + {{\varvec{R}}_{sa}}{{\varvec{\omega }}_a} + {{\varvec{F}}_{sa}}{{{\dot{\varvec{\eta }}}}_a} + {{\varvec{R}}_{sp}}{{\varvec{\omega }}_p})}& {}\nonumber \\ {+ {{\varvec{F}}_{sa}}{{{{\ddot{\varvec \eta }}}}_a} +{{\varvec{R}}_{sa}}{{{\dot{\varvec{\omega }}}}_a} +{{\varvec{R}}_{sp}}{{{\dot{\varvec{\omega }}}}_p} = }{{{\varvec{U}}_b} - {\varvec{T}}+ {\varvec{d}}} \end{aligned}$$
(2)
$$\begin{aligned} {{\varvec{I}}_{ai}}{{\dot{\varvec{\omega }}}_{ai}} + {{\varvec{F}}_{ai}}{{{\ddot{\varvec \eta }}}_{ai}} + {\varvec{R}}_{sai}^{\text{T}}{{\dot{\varvec{\omega }}}_b} = {{\varvec{U}}_{ai}}(i = -y,y) \end{aligned}$$
(3)
$$\begin{aligned} {{{\ddot{\varvec \eta }}}_{ai}} + 2{{\varvec{\zeta }}_{ai}}{{\varvec{\varOmega }}_{ai}}{{\dot{\varvec{\eta }}}_{ai}}\nonumber \\ + {{\varvec{\varLambda }}_{ai}}{{\varvec{\eta }}_{ai}} + {\varvec{F}}_{sa}^{\text{T}}{{\dot{\varvec{\omega }}}_b} + {\varvec{F}}_{ai}^{\text{T}}{{\dot{\varvec{\omega }}}_{ai}} = 0(i = - y, + y) \end{aligned}$$
(4)
$$\begin{aligned} {{\varvec{I}}_\mathrm{{p}}}{{\dot{\varvec{\omega }}}_p} + {\varvec{R}}_{sp}^{\text{T}}{{\dot{\varvec{\omega }}}_b} = {{\varvec{U}}_p} + {{\varvec{T}}_c} \end{aligned}$$
(5)

where \({{\varvec{F}}_{sa}}\) denotes the coupling coefficient matrix of the rotation of the spacecraft platform with the vibration of the solar panels, and \({{\varvec{F}}_{sa}} = {{\varvec{F}}_{+\mathrm{{sa}}y}} + {{\varvec{F}}_{ - say}}\). \({{\varvec{R}}_{sa}}\) is the coupling coefficient matrix of the rotation between the solar panels and the platform, where \({{\varvec{R}}_{sa}} = {{\varvec{R}}_{+\mathrm{{sa}}y}} + {{\varvec{R}}_{ - say}}\). \({\varvec{T}}\) denotes the external electromagnetic force acting on the spacecraft platform; the inertia matrix of the spacecraft platform is defined as \({\textbf{I}}_b\), satisfying the equation \({{\varvec{I}}_b} = {{\varvec{I}}_{b0}} + {{\varvec{C}}_{ba}}{{\varvec{I}}_{a0}}{\varvec{C}}_{ba}^{\text{T}}\); and \({{\varvec{{I}}}_{a0}}\) denotes the inertia matrix of the flexible solar panel when it is not rotating. \({{\varvec{U}}_b}\) denotes the torque of the spacecraft platform, and \({\varvec{d}}\) is the unknown external disturbance torque. \({{\varvec{T}}_c}\) denotes the projection of the resultant torque of the connect bearing of the platform. where i denotes the i-th solar panel installed on the platform, \({{\varvec{{I}}}_a}\) denotes the inertia matrix relative to the fixed coordinate system of the flexible solar panel, \({{\varvec{U}}_a}\) denotes the torque that comes from the control motor of the flexible solar panel, \({{\varvec{\eta }}_a}\) denotes the modal coordinates of the solar panel, \({{\varvec{\varOmega }}_a}\) denotes the diagonal matrix of the modal frequency of the solar panel, \({{\varvec{\varLambda }}_a}\) is the stiffness matrix of the solar panel such that \({{\varvec{\varLambda }}_a} = {\varvec{\varOmega }}_a^2\), and \({{\varvec{\zeta }}_a}\) is the damping ratio of the solar panel. Notably, these parameters are diagonal matrices. Where \({{\varvec{{I}}}_p}\) denotes the inertia matrix of the rigid rotation payload and \({{\varvec{U}}_p}\) denotes the torque that comes from the momentum wheel. \({{\varvec{\omega }}_p}\) is the actual attitude angular velocity, and \({{\varvec{R}}_{sp}}\) is the coupling coefficient matrix of the rotation between the payload and the platform.

Assuming that the flexible solar panels are installed in the Y-axis of the spacecraft platform and rotates relative to the Y-axis of the spacecraft system coordinate system, the rotation angle is defined as \({\theta _{ay}}\). The calculation of \({{\varvec{F}}_{sa}}\)is as follows [28]:

$$\begin{aligned} {{\varvec{F}}_{sa}} = \left[ {{f_{sa1}}\left[ {\begin{array}{*{20}{c}} {\sin ({\theta _{ay}})}\\ 1\\ {\cos ({\theta _{ay}})} \end{array}} \right] ,{f_{sa2}}\left[ {\begin{array}{*{20}{c}} {\sin ({\theta _{ay}})}\\ 1\\ {\cos ({\theta _{ay}})} \end{array}} \right] ,\ldots ,{f_{san}}\left[ {\begin{array}{*{20}{c}} {\sin ({\theta _{ay}})}\\ 1\\ {\cos ({\theta _{ay}})} \end{array}} \right] } \right] \end{aligned}$$
(6)

In order to determine the attitude transformation matrix of the spacecraft, if the relative attitude quaternion of the spacecraft is known, we can obtain the transformation matrix from Eq. (2). A direction cosine matrix can be obtained from the coordinate system ’a’to the coordinate system ’b’ based on the following formula.

$$\begin{aligned} {{\varvec{C}}_{ba}} = \left[ {\begin{array}{*{20}{c}} {q_0^2 + q_1^2 - q_2^2 - q_3^2}&{}{2({q_1}{q_2} + {q_0}{q_3})}&{}{2({q_1}{q_3} - {q_0}{q_2})}\\ {2({q_1}{q_2} - {q_0}{q_3})}&{}{q_0^2 - q_1^2 + q_2^2 - q_3^2}&{}{2({q_2}{q_3} + {q_0}{q_1})}\\ {2({q_1}{q_3} + {q_0}{q_2})}&{}{2({q_2}{q_3} - {q_0}{q_1})}&{}{q_0^2 - q_1^2 - q_2^2 + q_3^2} \end{array}} \right] \end{aligned}$$
(7)

Thus, the calculation formulas for the angular velocity and quaternion errors of the spacecraft platform are defined as follows:

$$\begin{aligned} {{\varvec{\omega }}_{be}}&= {{\varvec{\omega }}_b} - {\varvec{C}}{{\varvec{\omega }}_{bd}} \end{aligned}$$
(8)
$$\begin{aligned} {{\varvec{q}}_e}&= \left[ {\begin{array}{*{20}{c}} {{q_{e0}}}\\ {{{\varvec{q}}_{ev}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{q_0}{q_{d0}} + {\varvec{q}}_d^{\text{T}}{{\varvec{q}}_d}}\\ {{q_{d0}}{{\varvec{q}}_v} + {{{\varvec{\tilde{q}}}}_v}{{\varvec{q}}_{dv}} - {q_0}{{\varvec{q}}_{dv}}} \end{array}} \right] \end{aligned}$$
(9)

where \({{\varvec{\omega }}_{be}}\) is the angular velocity error when the spacecraft platform is relative to the reference coordinate system , \({{\varvec{\omega }}_{b}}\) is the actual attitude angular velocity and \({{\varvec{\omega }}_{bd}}\) is the desired attitude angular velocity of the spacecraft platform relative to the spacecraft system reference frame , \({\varvec{C}}\) represents the transformation matrix from the actual coordinate system to the reference coordinate system. Similarly, the angular velocity and error angular velocity of the rotating appendage can be obtained. The angle of the flexible panel relative to the Y-axis of the spacecraft platform is \({{\varvec{\theta }}_a}\in \left( {0, + \infty } \right)\). The calculation formula is expressed as follows:

$$\begin{aligned}&{{\varvec{\omega }}_{ae}} = {{\varvec{\omega }}_a} - {{\varvec{\omega }}_{ad}} \end{aligned}$$
(10)
$$\begin{aligned}&{{\varvec{\theta }}_a} = \int {{{\varvec{\omega }}_a}} dt \end{aligned}$$
(11)

where \({{\varvec{\omega }}_{a}}\) is the actual attitude angular velocity. Similarly, the angular and error angular velocity of rotating appendage can be obtained. Considering the actuator faults and uncertainty of the spacecraft, the actuator output torque is:

$$\begin{aligned} {{\varvec{U}}_b} = {\varvec{E}}{{\varvec{u}}_b} = {\varvec{E\sigma u}} \end{aligned}$$
(12)

where \({{\varvec{E}}_{3 \times n}}\) is the installation matrix of the spacecraft actuator, \({{\varvec{u}}_i}\) is the output torque of the spacecraft actuator calculated according to the control law, \({\varvec{\sigma }}\; = \;\text{diag}\left\{ {{\sigma _1},{\sigma _2}, \cdots ,{\sigma _n}} \right\}\), \({\sigma _i}\) is the failure coefficient of the i-th reaction wheel and it satisfies \(0 \le {\sigma _i} \le 1\);\({\sigma _i} = 0\) means the reaction wheel is completely stuck and the output torque is 0, \({\sigma _i} = 1\) means the reaction wheel normally working and the output torque is max, \(0< {\sigma _i} < 1\) means the output torque value of reaction wheel is between the maximum and minimum. It is further assumed that \({{\varvec{J}}_b} = {{\varvec{I}}_b} - {{\varvec{R}}_{sa}}{({{\varvec{I}}_a} - {{\varvec{F}}_a}{\varvec{F}}_a^{\text{T}})^{ - 1}}({\varvec{R}}_{sa}^{\text{T}} - {{\varvec{F}}_a}{\varvec{F}}_{sa}^{\text{T}}) - {{\varvec{R}}_{sp}}{\varvec{R}}_{sp}^{\text{T}}\), \({{\varvec{J}}_a} = ({{\varvec{I}}_a} - {{\varvec{F}}_a}{\varvec{F}}_a^{\text{T}})\) and \({{\varvec{H}}_a} = ({{\varvec{R}}_{sa}} - {{\varvec{F}}_{sa}}{\varvec{F}}_a^{\text{T}})\), Then according the formula (8),(10)and (12) can be rewritten as:

$$\begin{aligned} \begin{array}{*{20}{l}} {{{\varvec{J}}_{b0}}{{{\dot{\varvec{\omega }}}}_{be}}}&{}={{\varvec{E}}{{\varvec{u}}_b} - {{\varvec{J}}_{b0}}\left( {C{{{\dot{\varvec{\omega }}}}_{bd}} - {{{{\tilde{\varvec \omega }}}}_{be}}{\varvec{C}}{{\varvec{\omega }}_{bd}}} \right) - {{\varvec{T}}_r} - {{\varvec{F}}_{sa}}{{{{\ddot{\varvec \eta }}}}_a} - {{{{\tilde{\varvec \omega }}}}_b}{{\varvec{F}}_{sa}}{{{\dot{\varvec{\eta }}}}_a}}\\ {}&{}{- {{{{\tilde{\varvec \omega }}}}_b}({{\varvec{I}}_{b0}}{{\varvec{\omega }}_b} + {{\varvec{R}}_{sa}}{{\varvec{\omega }}_a} + {{\varvec{R}}_{sp}}{{\varvec{\omega }}_p}) - {\varvec{f}}} \end{array} \end{aligned}$$
(13)
$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{{{\dot{\varvec{\omega }}}}_{ae}}}\\ {{{{\dot{\varvec{\omega }}}}_{pe}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}}&{}0\\ 0&{}{\varvec{I}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{U_a}}\\ {{{\varvec{U}}_p}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{\varvec{H}}_a^{\text{T}}}\\ {{\varvec{R}}_{sp}^{\text{T}}} \end{array}} \right] {{\dot{\varvec{\omega }}}_b} + \left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}{{\varvec{F}}_a}{\vartheta _\eta }}\\ {{{\varvec{T}}_c}} \end{array}} \right] \end{aligned}$$
(14)

where it is defined that \({{\varvec{T}}_r} = \left( {{{\varvec{R}}_{sp}} + {\varvec{I}}} \right) {{\varvec{T}}_c} + {{\varvec{R}}_{sa}}{\varvec{J}}_a^{ - 1}{{\varvec{U}}_a} + {{\varvec{R}}_{sp}}{{\varvec{U}}_p}\) and \({\varvec{f}} = - {\varvec{d}} + {{\varvec{R}}_{sa}}{\varvec{J}}_a^{ - 1}{{\varvec{F}}_a}{\vartheta _\eta } + \varDelta {{\varvec{J}}_b}{{\dot{\varvec{\omega }}}_{be}}\) \(+ \varDelta {{\varvec{J}}_b}\left( {{\varvec{C}}{{{\dot{\varvec{\omega }}}}_{bd}} - {{{{\tilde{\varvec \omega }}}}_{be}}{\varvec{C}}{{\varvec{\omega }}_{bd}}} \right) + {{\tilde{\varvec{\omega }}}_b}\varDelta {{\varvec{I}}_b}{{\varvec{\omega }}_b} + \hbar \left( {\varDelta {{\varvec{R}}_{sa}},\varDelta {{\varvec{R}}_{sp}},\varDelta {{\varvec{F}}_{sa}}} \right)\).

Remark 1

 [29]: The moment of inertia of the spacecraft system has the specific form of \({\varvec{J}} = {{\varvec{J}}_0} + \varDelta {\varvec{J}}\), where \({{\varvec{J}}_0}\) is the nominal constant matrix, and \(\varDelta {\varvec{J}}\) is the uncertainty in the moment of inertia and is a bounded constant.

Remark 2

 [30]: The spacecraft platform and flexible solar panels have a coupling effect, where \({\delta _1}{{{\ddot{\varvec \eta }}}_a} + {\tilde{\omega }_b}{\delta _3}{{\dot{\varvec{\eta }}}_a}\) should satisfy \(\left\| {{\delta _1}{{{\dot{\varvec{\eta }}}}_a} + {{{{\tilde{\varvec \omega }}}}_b}{\delta _3}{{{\dot{\varvec{\eta }}}}_a}} \right\| \le {b_1} + {b_2}{\left\| {\varvec{\omega }} \right\| ^2}\), \({b_1} > 0\) and \({b_2} > 0\). Thus, the following \(\left\| {{\delta _1}{{{{\ddot{\varvec \eta }}}}_a} + \tilde{\omega }{\delta _3}{{{\dot{\varvec{\eta }}}}_a}} \right\| \le \mu (1 + {\left\| {\varvec{\omega }} \right\| ^2})\) inequality can be obtained, and \(\mu = max\left( {{b_1},{b_2}} \right)\).

Remark 3

 [30] The angular velocity of the system and its accessories and its first derivative are bounded, where \({{\dot{\varvec{\omega }}}_b} \le {{\varvec{\omega }}_r}\).

3 Attitude Control Law Design for the Spacecraft Platform and Rotating Appendages

In this paper, an adaptive fuzzy sliding mode (AFS) controller is designed for the spacecraft platform, and a fixed-time sliding mode controller is designed for the rotating appendages. The control principle diagram of the spacecraft system structure is shown in Fig. 2.

Fig. 2
figure 2

The structure of Fuzzy controller

Full size image

Before designing the controller, we introduce the following concepts and lemmas, which are utilised in the design of the attitude controller. Consider the nonlinear system

$$\begin{aligned} \dot{x}(t) = f(x(t)),x(0) = 0,f(0) = 0 \end{aligned}$$
(15)

where \(x \in {R^n}\) and \(f\left( x \right)\) is a nonlinear continuous function, and it becomes continuous in an open neighbourhood of the origin \(x = 0\).

Lemma 1

 [31]—[32]. For the system of formula (refeq15), we suppose that there is a continuous differential Lyapunov function V(x) defined on its neighbourhood of origin, and if

$$\begin{aligned} \dot{V}\left( x \right) + {\lambda _1}V\left( x \right) + {\lambda _2}V\left( x \right) \le 0 \end{aligned}$$
(16)

where \({\lambda _1},{\lambda _2} \in {R^ + }\) and \(0< \alpha < 1\), The system can then reach \(V(x) \equiv 0\) in a finite time, and its convergence time T is:

$$\begin{aligned} T \le \frac{1}{{{\lambda _1}\left( {1 - p} \right) }}\ln \left( {\frac{{{\lambda _1}}}{{{\lambda _2}}}{{\big | {V\left( 0 \right) } \big |}^{1 - p}} + 1} \right) \end{aligned}$$
(17)

Else if the function V(x) satisfies,

$$\begin{aligned} \dot{V}(x) + {({\lambda _1}{V^p}(x) + {\lambda _2}{V^g}(x))^k} \le 0 \end{aligned}$$
(18)

where \(\alpha ,\beta ,g,p,k \in {R^ + }\) \(pk < 1\) and \(gk > 1\). The system can then reach in a fixed time, and its convergence time is:

$$\begin{aligned} T \le \frac{1}{{{\lambda _1}^k\left( {1 - pk} \right) }} + \frac{1}{{{\lambda _2}^k\left( {gk - 1} \right) }} \end{aligned}$$
(19)

Lemma 2

 [33]. For any \(x \in {R^n}\) and \(a \in R\), the following operation holds:

$$\begin{aligned} \frac{{\text{d}{{\big | x \big |}^{\gamma + 1}}}}{{\text{d}t}} = (\gamma + 1)\text{diag}(\text{sig}{(x)^\gamma })\dot{x}\end{aligned}$$
(20)
$$\begin{aligned} \frac{{\text{dsig}{{(x)}^{\gamma + 1}}}}{{\text{d}t}} = (\gamma + 1)\text{diag}{(\big | x \big |)^\gamma })\dot{x} \end{aligned}$$
(21)

Remark 4

 [7] There exist some inequalities as:

$$\begin{aligned} {x^{\text{T}}}y \le \frac{1}{2}{m^{ - 2}}{\left\| x \right\| ^2} + \frac{1}{2}{m^2}{\left\| y \right\| ^2}\end{aligned}$$
(22)
$$\begin{aligned} {A^{\text{T}}}W\xi \le \frac{1}{2}{\varepsilon ^{ - 2}}{\left\| A \right\| ^2}{\left\| W \right\| ^2}{\left\| \xi \right\| ^2} + \frac{1}{2}{\varepsilon ^2}\end{aligned}$$
(23)
$$\begin{aligned} {A^{\text{T}}}d \le \frac{1}{2}{\varepsilon ^{ - 2}}{\left\| A \right\| ^2}{\left\| d \right\| ^2} + \frac{1}{2}{\varepsilon ^2} \end{aligned}$$
(24)

3.1 Adaptive Fuzzy Sliding Mode Controller Description

The basic structure of the fuzzy-logic system controller is shown in Fig. 3. It usually consists of four parts: a fuzzifier, knowledge base, fuzzy inference, and defuzzifier [34]–[35]. The four parts of a fuzzy system determine a multi-input single-output structure, where U is a compact set. The fuzzifier maps the clarity variables that are generally obtained by calculation or sampling input space U to the fuzzy sets defined in U, and the defuzzifier performs an assignment to map fuzzy sets in R to a crisp point in R. The knowledge base consists of a set of rules in the form of “if-then” that have the following form [36]:

Fig. 3
figure 3

The structure of Fuzzy controller

Full size image

In the fuzzy control algorithm, the input variable is generally composed of multiple continuous clear components obtained by calculation or sampling.The essence of the transformation function of the scaling factor in the fuzzy control algorithm is to enlarge or reduce the range of the input signal and map the clear value to the fuzzy domain to meet the mapping requirements. In contrast, the fuzzy quantity must be transformed into a clear control quantity before it can be used by the actuator.We can separately set the input and output scaling factor as \({k_{in}}\) and \({k_{out}}\).The knowledge base contains a set of fuzzy “if-then” rules in as following:

$$\begin{aligned} {R^i}:\text{if}\; {x_1} \;is\; P_1^i \;\text{and}\;{\text{if}}\; {x_2}\; \text{is}\; P_2^i \;\text{and}\;{\text{if}}\; {x_n} \;\text{is} \;P_n^i,\nonumber \\ then \;{u_k} \;\text{is} \;U_k^i, i = 1,2, \cdots m \end{aligned}$$
(25)

where \(x = {\left[ {{x_1},{x_2}, \cdots ,{x_n}} \right] ^{\text{T}}}\) and \({u_k}\) denote the input and output of Fuzzy logic system(FLS), respectively, \(P_n^i\)and \({U^i}\) are linguistic terms characterized by their membership functions, and m is the number of rules. The output of the Fuzzy logic system can be obtained using center-average defuzzification [37].

$$\begin{aligned} u = \frac{{\sum \nolimits _{i = 1}^m {{{\bar{y}}_i}} \prod \limits _{j = 1}^n {{\mu _{P_j^i}}\left( {{x_j}} \right) } }}{{\sum \nolimits _{i = 1}^m {\left[ {\prod \limits _{j = 1}^n {{\mu _{P_j^i}}\left( {{x_j}} \right) } } \right] } }} \end{aligned}$$
(26)

In formula (26), where \({\bar{y}_i} = \max {u_{{U^i}}}\left( y \right)\), the adjustable system vector is denoted as \(w = {\left[ {{{\bar{y}}_1},{{\bar{y}}_2}, \cdots {{\bar{y}}_m}} \right] ^{\text{T}}}\) and defines the fuzzy basic function as

$$\begin{aligned} {\xi ^i}\left( x \right) = \frac{{\prod \limits _{j = 1}^n {{\mu _{P_j^i}}\left( {{x_j}} \right) } }}{{\sum \nolimits _{i = 1}^m {\left[ {\prod \limits _{j = 1}^n {{\mu _{P_j^i}}\left( {{x_j}} \right) } } \right] } }} \end{aligned}$$
(27)

If this can define a nonlinear function that can be approximated by the following form, according to the aforementioned fuzzy logic system [22].

$$\begin{aligned} {g_i}\left( x \right) = k_{\text{out}}^i{w_i}\xi \left( x \right) + {\varepsilon _i} \end{aligned}$$
(28)

Then the continuous nonlinear function can be approximated by \({\varvec{G}}\left( x \right) = {\varvec{KW\xi }}\left( x \right) + {\varvec{\delta }}\),

$$\begin{aligned} {\varvec{W}} = \left[ {{w_1},{w_2}, \cdots {w_m}} \right] \end{aligned}$$

and

$$\begin{aligned} {\varvec{\varepsilon }} = \left[ {{\varepsilon _1},{\varepsilon _2}, \cdots {\varepsilon _m}} \right] . \end{aligned}$$

Lemma 3

 [38] The \(f\left( x \right)\) is a continuous function, which is defined on a compact set U .Then there exists a FLS \(\sup \big | {f\left( x \right) - {k_{out}}\tau \xi \left( x \right) } \big | \le \varepsilon\) for any constant \(\varepsilon > 0\).thus ,it can obtain:

$$\begin{aligned} {\varvec{\varTheta }} \le {\varvec{\varPhi }} = {\varvec{W\xi }}\left( {\omega ,q} \right) + {\varvec{d}} \end{aligned}$$
(29)

Define the vector

$$\begin{aligned} {\varvec{\rho }} = \left[ {\begin{array}{*{20}{c}} {{{\left\| {\varvec{W}} \right\| }^2}}\\ {{{\left\| {\varvec{d}} \right\| }^2}} \end{array}} \right] \end{aligned}$$

and \({\varvec{\theta }} = \left[ {\begin{array}{*{20}{c}} {{{\left\| {\varvec{\xi }} \right\| }^2}}\\ 1 \end{array}} \right]\) The adaptive updating law is given as:

$$\begin{aligned} {\dot{{\hat{\varvec \rho }} }} = \frac{1}{2}{\varvec{\tau }}{\left\| {{\varvec{J}}_{b0}^{ - T}{\varvec{S}}} \right\| ^2}{\varvec{\theta }} - {{\sigma \hat{\varvec \rho }}} \end{aligned}$$
(30)

And the fuzzy adaptive control law can be obtained:

$$\begin{aligned} {{\varvec{U}}_{\text{fuadp}}} = - \frac{1}{{2{\varepsilon ^2}}}{{\hat{\varvec{\rho }}}^{\text{T}}}{\varvec{\theta J}}_{b0}^{ - T}{\varvec{S}} \end{aligned}$$
(31)

There are numerous related literatures on spacecraft attitude control. Scholars have proposed a variety of spacecraft attitude control methods [39]. Based on some researches, this paper designs the following sliding mode surface.

$$\begin{aligned} {\varvec{S}_b} = {{\varvec{\omega }}_{be}} + {{\varvec{k}}_1}*{{\varvec{q}}_{be}} + {{\varvec{k}}_2}*\text{sig}{^\alpha }\left( {{{\varvec{q}}_{be}}} \right) \end{aligned}$$
(32)

where \({{\varvec{k}}_1}{{ = \text{diag}(}}{\mathrm{{k}}_{11}}, {\mathrm{{k}}_{12}}, {\mathrm{{k}}_{13}}\mathrm{{)}}\) and \({{\varvec{k}}_2}{{ = \text{diag}(}}{\mathrm{{k}}_{21}}, {\mathrm{{k}}_{22}}, {\mathrm{{k}}_{23}}\mathrm{{)}}\) \({k_{ii}} > 0\),the function can be defined as \({\text{sig}}^{\alpha }\left( {{q_e}} \right) = \left[ {{{\big | {{q_{e1}}} \big |}^\alpha }\text{sign}\left( {{q_{e1}}} \right) ,{{\big | {{q_{e2}}} \big |}^\alpha }\text{sign}\left( {{q_{e2}}} \right) , \cdots ,{{\big | {{q_{ei}}} \big |}^\alpha }\text{sign}\left( {{q_{ei}}} \right) } \right]\), respectively \(0< \alpha < 1\). the control scheme of of platform consist of three parts:can obtain:

$$\begin{aligned} {{\varvec{U}}_b} = {\varvec{E}}{{\varvec{u}}_b} = {{\varvec{U}}_1} + {{\varvec{U}}_2} + {{\varvec{U}}_{{\text{fuadp}}}} \end{aligned}$$
(33)

where

$$\begin{aligned} {\varvec{U}_1} = {\varvec{T}_r} + {b_0}{\left\| \omega \right\| ^2} + {{\varvec{J}}_{b0}}\left( {{\varvec{C}}{{{\dot{\varvec{\omega }}}}_{bd}} - {{{{\tilde{\varvec \omega }}}}_{be}}{\varvec{C}}{{\varvec{\omega }}_{bd}}} \right) \\ + {{\tilde{\varvec{\omega }}}_b}\left( {{{\varvec{I}}_{b0}}{{\varvec{\omega }}_b} + {{\varvec{R}}_{sa}}{{\varvec{\omega }}_a} + {{\varvec{R}}_{sp}}{{\varvec{\omega }}_p}} \right) \\ \begin{array}{*{20}{l}} {{{\varvec{U}}_2} = }&{}{ - \frac{1}{2}{{\varvec{J}}_{b0}}\left[ {{{\varvec{k}}_1} + \alpha {{\varvec{k}}_2}*\text{diag}\left( {{{\big | {{{\varvec{q}}_{be}}} \big |}^{\alpha - 1}}} \right) } \right] *{\varvec{Q}}\left( {{{\varvec{q}}_{be}}} \right) * {{\varvec{\omega }}_{be}}}\\ {}&{}{ - {{\varvec{J}}_{b0}}{{\varvec{c}}_1}sign({\varvec{S_b}}) - {{\varvec{J}}_{b0}}{{\varvec{c}}_2}{\varvec{S_b}}} \end{array} \end{aligned}$$

Theorem 1

 [28]: For the flexible coupling spacecraft platform,\({{\varvec{S}}_b}\) and \({{\hat{\varvec \rho }}}\) are uniformly ultimately bounded with the control scheme in adaptive fuzzy sliding laws.

Proof

The Lyapunov’s second method is often used to prove the stability of the system [40], We consider the candidate Lyapunov function:

$$\begin{aligned} {{\varvec{V}}_b} = \frac{1}{2}{\varvec{S}}_b^{\text{T}}{\varvec{J}}{{\varvec{S}}_b} + \frac{1}{{2\tau \gamma }}{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) ^{\text{T}}}\left( {\rho - \gamma {{\hat{\varvec \rho }}}} \right) \end{aligned}$$
(34)

Because \({\dot{\varvec{S}}} = {{\dot{\varvec{\omega }}}_{be}} + {{\varvec{k}}_1}{{\dot{\varvec{q}}}_{be}} + \alpha {{\varvec{k}}_2}\text{diag}({\big | {{{\varvec{q}}_{be}}} \big |^{\alpha - 1}}){{\dot{\varvec{q}}}_{be}}\),the derivative of \({{\varvec{V}}_b}\) along the trajectory of the spacecraft platform. we can obtain

$$\begin{aligned}&\quad {{{{\dot{\varvec{V}}}}_b}}= {S_b^{\text{T}}{{{\dot{\varvec{S}}}}_b} - \frac{1}{\tau }{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho } }}} \right) }^{\text{T}}}{{\dot{\hat{\varvec \rho }} }}}\nonumber \\&\quad ={{\varvec{S}}_b^{\text{T}}\left\{ {{{{\dot{\varvec{\omega }}}}_e} + \left[ {{{\varvec{k}}_1} + \alpha {{\varvec{k}}_2}\text{diag}({{\big | {{{\varvec{q}}_e}} \big |}^{\alpha - 1}})} \right] {{{\dot{\varvec{q}}}}_e}}\right\} }\nonumber \\&\quad - \frac{1}{\tau }{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho } }}} \right) } ^{\text{T}}}{{\dot{\hat{\varvec \rho }} }}\nonumber \\&\quad ={\varvec{S}}_b^{\text{T}}\left\{ {\varvec{J}}_{b0}^{ - 1}\left[ {\varvec{E}}{{\varvec{u}}_b} - {{\varvec{J}}_{b0}}\left( {{\varvec{C}}{{{\dot{\varvec{\omega }}}}_{bd}} - {{{{\tilde{\varvec \omega }}}}_{be}}{\varvec{C}}{{\varvec{\omega }}_{bd}}} \right) - {{\varvec{T}}_r}\right. \right. \nonumber \\&\quad \left. \left. -{{\varvec{F}}_{sa}}{{{{\ddot{\varvec \eta }}}}_a} - {{{{\tilde{\varvec \omega }}}}_b}{{\varvec{F}}_{sa}}{{{\dot{\varvec{\eta }}}}_a} \right] \right\} \nonumber \\&\quad +{\varvec{S}}_b^{\text{T}}\left\{ {\varvec{J}}_{b0}^{ -1}\left[ - {{{{\tilde{\varvec \omega }}}}_b}({{\varvec{I}}_{b0}}{{\varvec{\omega }}_b}\right. \right. \nonumber \\&\quad \left. \left. + {{\varvec{R}}_{sa}}{{\varvec{\omega }}_a} +{{\varvec{R}}_{sp}}{{\varvec{\omega }}_p} - {\varvec{\varTheta }} \right] \right\} - \frac{1}{\tau }{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho } }}} \right) }^{\text{T}}}{{\dot{\hat{\varvec \rho }} }}\nonumber \\&\quad +{\varvec{S}}_b^{\text{T}}\left\{ {\frac{1}{2}\left[ {{{\varvec{k}}_1}+ \alpha {{\varvec{k}}_2}\text{diag}({{\big |{{{\varvec{q}}_e}} \big |}^{\alpha - 1}})}\right] {{\varvec{Q}}_{be}}{{\varvec{\omega }}_{be}}} \right\} \end{aligned}$$
(35)

\(\square\)

Substituting (33) into the equation, we can obtain:

$$\begin{aligned}&\quad {{\dot{\varvec{V}}_b}}={\varvec{S}}_b^{\text{T}}\left\{ {\varvec{J}}_{b0}^{ - 1}\left[ {{\varvec{U}}_1} + {{\varvec{U}}_2} + {\varvec{U}}_{fuadp}\right. \right. \\&\quad \left. \left. - {{\varvec{J}}_{b0}}\left( {{\varvec{C}}{{{\dot{\varvec{\omega }}}}_{bd}} - {{{{\tilde{\varvec \omega }}}}_{be}}{\varvec{C}}{{\varvec{\omega }}_{bd}}} \right) - {{\varvec{T}}_r} -{{\varvec{F}}_{sa}}{{{{\ddot{\varvec \eta }}}}_a} \right] \right\} \\&\quad + {\varvec{S}}_b^{\text{T}}\left\{ {\varvec{J}}_{b0}^{ -1} \left[ - {{{{\tilde{\varvec \omega }}}}_b}{{\varvec{F}}_{sa}}{{{\dot{\varvec{\eta }}}}_a}\right. \right. \\&\quad \left. \left. - {{{{\tilde{\varvec \omega }}}}_b}({{\varvec{I}}_{b0}}{{\varvec{\omega }}_b} + {{\varvec{R}}_{sa}}{{\varvec{\omega }}_a} + {{\varvec{R}}_{sp}}{{\varvec{\omega }}_p}) - {\varvec{\varTheta }} \right] \right\} \\&\quad + {\varvec{S}}_b^{\text{T}}\left\{ {\frac{1}{2}\left[ {{{\varvec{k}}_1} + \alpha {{\varvec{k}}_2}\text{diag}({{\big |{{\varvec{q}}_e} \big |}^{\alpha - 1}})}\right] {{\varvec{Q}}_{be}}{{\varvec{\omega }}_{be}}} \right\} \\&\quad -\frac{1}{\tau }{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho } }}} \right) }^{\text{T}}}{{\dot{\hat{\varvec \rho }} }}\\&\quad = {\varvec{S}}_b^{\text{T}}\left\{ {\varvec{J}}_{b0}^{ - 1}\left[ {b_0}{{\big \Vert {\varvec{\omega }} \big \Vert }^2} + {{\varvec{U}}_2} +{{\varvec{U}}_{fuadp}}\right. \right. \\&\quad \left. \left. - {{\varvec{F}}_{sa}}{{{{\ddot{\varvec \eta }}}}_a} - {{{{\tilde{\varvec \omega }}}}_b}{{\varvec{F}}_{sa}}{{{\dot{\varvec{\eta }}}}_a} - {\varvec{\varTheta }} \right] \right\} \\&\quad + {\varvec{S}}_b^{\text{T}}\left\{ {\frac{1}{2}\left[ {{{\varvec{k}}_1} + \alpha {{\varvec{k}}_2}\text{diag}({{\big | {{{\varvec{q}}_e}} \big |}^{\alpha - 1}})} \right] {{\varvec{Q}}_{be}}{{\varvec{\omega }}_{be}}} \right\} \\&\quad -\frac{1}{\tau }{{\left( {{\varvec{\rho }} - \gamma {\hat{\varvec{\rho } }}} \right) }^{\text{T}}}{{\dot{\hat{\varvec \rho }} }} \end{aligned}$$

Thus, according to relevant theorems and inequalities, we also can obtain:

$$\begin{aligned}&{{{{\dot{\varvec{V}}}}_b}} \le {\varvec{S}}_b^{\text{T}}{\varvec{J}}_{b0}^{ -1} \left[ {b_0}{{\left\| {\varvec{\omega }} \right\| }^2} - \frac{1}{2}{\varepsilon ^{ - 2}}{{{\hat{\varvec \rho }}}^{\text{T}}} {\varvec{\theta J}}_{b0}^{ - T}{{\varvec{S}}_b}+ {\varvec{W\xi }}+ {\varvec{d}}\right. \\&\quad \left. - {{\varvec{F}}_{sa}}{{{{\ddot{\varvec \eta }}}}_a} - {{{{\tilde{\varvec \omega }}}}_b}{{\varvec{F}}_{sa}}{{{\dot{\varvec{\eta }}}}_a}\right] \\&\quad { - {\varvec{S}}_b^{\text{T}}\left[ {{{\varvec{c}}_1}\text{sign}({{\varvec{S}}_b}) + {{\varvec{c}}_2}{{\varvec{S}}_b}} \right] - \frac{1}{\tau }{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho } }}} \right) }^{\text{T}}}{{\dot{\hat{\varvec \rho }} }}}\\&\quad \le { - \frac{1}{{2{\varepsilon ^2}}}{{{{\hat{\varvec \rho }}}}^{\text{T}}}{\varvec{\theta }}\gamma {\varvec{S}}_b^{\text{T}}{\varvec{J}}_{b0}^{ - 1}{\varvec{J}}_{b0}^{ - T}{{\varvec{S}}_b} + {\varvec{S}}_b^{\text{T}}{\varvec{J}}_{b0}^{ - 1}\left( {{\varvec{W\xi + d}}} \right) }\\&\quad { - {\varvec{S}}_b^{\text{T}}\left[ {{{\varvec{c}}_1}\text{sign}({{\varvec{S}}_b}) + {{\varvec{c}}_2}{{\varvec{S}}_b}} \right] - \frac{1}{\tau }{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho } }}} \right) }^{\text{T}}}{{\dot{\hat{\varvec \rho }} }}}\\&\quad \le { - \frac{1}{{2{\varepsilon ^2}}}{{{{\hat{\varvec \rho }}}}^{\text{T}}}{\varvec{\theta }}\gamma {\varvec{S}}_b^{\text{T}}{\varvec{J}}_{b0}^{ - 1}{\varvec{J}}_{b0}^{ - T}{{\varvec{S}}_b} + \frac{1}{{2{\varepsilon ^2}}}{{\varvec{\rho }}^{\text{T}}}{\varvec{\theta J}}_{b0}^{ - T}{\varvec{S}}_b^{\text{T}}{{\varvec{S}}_b}{\varvec{J}}_{b0}^{ - 1} + {{\varvec{\varepsilon }}^2}}\\&\quad { - \frac{1}{\tau }{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) }^{\text{T}}}\left( {\frac{1}{{2{\varepsilon ^2}}}\tau {\varvec{J}}_{b0}^{ - T}{{\left\| {{{\varvec{S}}_b}} \right\| }^2}{\varvec{J}}_{b0}^{ - 1}{\varvec{\theta }} - \sigma {{\hat{\varvec \rho }}}} \right) }\\&\quad { - {\varvec{S}}_b^{\text{T}}\left[ {{c_1}\text{sign}({{\varvec{S}}_b}) + {{\varvec{c}}_2}{{\varvec{S}}_b}} \right] }\\ {}= & {} {{{\varvec{\varepsilon }}^2} - {\varvec{S}}_b^{\text{T}}\left[ {{c_1}\text{sign}({{\varvec{S}}_b}) + {{\varvec{c}}_2}{{\varvec{S}}_b}} \right] + \frac{\sigma }{\tau }{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) }^{\text{T}}}{{\hat{\varvec \rho }}}}\\&\quad \le {{{\varvec{\varepsilon }}^2} - {\varvec{S}}_b^{\text{T}}\left[ {{c_1}\text{sign}({{\varvec{S}}_b}) + {{\varvec{c}}_2}{{\varvec{S}}_b}} \right] + \frac{\sigma }{{2\tau \gamma }}\left( {{{\varvec{\rho }}^{\text{T}}}{\varvec{\rho }} - \gamma {{{{\hat{\varvec \rho }}}}^{\text{T}}}{{\hat{\varvec \rho }}}} \right) }\\&\quad { - \frac{\sigma }{{2\tau \gamma }}{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) }^{\text{T}}}\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) }\\&\quad \le {{{\varvec{\varepsilon }}^2} - {\varvec{S}}_b^{\text{T}}\left[ {{c_1}\text{sign}({{\varvec{S}}_b}) + {{\varvec{c}}_2}{{\varvec{S}}_b}} \right] + \frac{\sigma }{{2\tau \gamma }}{{\varvec{\rho }}^{\text{T}}}{\varvec{\rho }}}\\ {}{} & {} { - \frac{\sigma }{{2\tau \gamma }}{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) }^{\text{T}}}\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) }\\&\quad \le {{{\varvec{\varepsilon }}^2} - {\varvec{S}}_b^{\text{T}}\left[ {{c_1}\text{sign}({{\varvec{S}}_b}) + {{\varvec{c}}_2}{{\varvec{S}}_b}} \right] + \frac{\sigma }{{2\tau \gamma }}({{\varvec{W}}^4} + {{\varvec{d}}^4})}\\&\quad { - \frac{\sigma }{{2\tau \gamma }}{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) }^{\text{T}}}\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) }\\&\quad \le { - {\lambda _{\min }}\left( {{{\varvec{c}}_2}} \right) {\varvec{S}}_b^{\text{T}}{{\varvec{S}}_b} - \frac{\sigma }{{2\tau \gamma }}{{\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) }^{\text{T}}}\left( {{\varvec{\rho }} - \gamma {{\hat{\varvec \rho }}}} \right) + {\varvec{\varsigma }}}\\&\quad { - \kappa {\varvec{V}_b} + {\varvec{\varsigma }}} \end{aligned}$$

where \({\varvec{\varsigma }} = \frac{\sigma }{{2\tau \gamma }}({{\varvec{W}}^4} + {{\varvec{d}}^4}) + {{\varvec{\varepsilon }}^2}\) and \(\kappa = \min \left\{ {{\lambda _{\min }}\left( {{c_2}} \right) ,{{{\sigma _2}} /\gamma }} \right\}\),and the state of platform are uniformly ultimately bounded. This shows that the platform system is finally stable.

3.2 The Control Law Design of Appendages

For the appendages, bilateral symmetrical flexible solar panels are installed in the Y-axis direction of the spacecraft platform ,and a rigid rotating payload is installed in the X-axis direction connecting with the spacecraft platform by bearing. we propose an appropriate fixed-time control scheme to make them rotate stably.

$$\begin{aligned} {{\varvec{S}}_r} = {{\varvec{\omega }}_{re}} + \text{sig}{\left[ {{{\varvec{c}}_1}*{\varvec{q}}_{re}^m + {{\varvec{c}}_2}*\text{sig}{^n}\left( {{{\varvec{q}}_{re}}} \right) } \right] ^{0.5}} \end{aligned}$$
(36)

where the parameter matrices are \({{\varvec{c}}_1} = \text{diag}\left[ {{c_{a11}},{c_{a12}},{c_{a13}},{c_{p11}},{c_{p12}},{c_{p13}}} \right]\) and \({{\varvec{c}}_2} = \text{diag}\left[ {{c_{a21}},{c_{a22}},{c_{a23}},{c_{p21}},{c_{p22}},{c_{p23}}} \right]\), respectively, \({c_{ii}}> 0,m < 2,n > 2\). Let \({{\varvec{x}}_r} = \text{diag}\left( {{{\big | {{{\varvec{c}}_1}*{\varvec{q}}_{re}^m + {{\varvec{c}}_2}*\text{sig}{^n}\left( {{{\varvec{q}}_{re}}} \right) } \big |}^{ - 0.5}}} \right)\). the torque of appendages can obtain:

$$\begin{aligned} \begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {{{\varvec{U}}_a}}\\ {{{\varvec{U}}_p}} \end{array}} \right] = }&{}{ - \left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}{{\varvec{F}}_a}{\vartheta _\eta }}\\ {{{\varvec{T}}_c}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{\varvec{J}}_a}{\varvec{H}}_a^{\text{T}}}\\ {{\varvec{R}}_{sp}^{\text{T}}} \end{array}} \right] {{\varvec{\omega }}_\gamma } - {{\left[ {{\tau _1}{{\varvec{S}}_r} + {\tau _2}\text{sat}{^{\text{T}}}\left( {{{\varvec{S}}_r}} \right) } \right] }^{0.5}}}\\ {}&{}{ - \frac{1}{4}{{\varvec{x}}_r}\left[ {{{\varvec{c}}_1}m{\varvec{q}}_{re}^{m - 1} + {{\varvec{c}}_2}n\text{sig}{^{n - 1}}\left( {{{\varvec{q}}_{re}}} \right) } \right] \left[ {\begin{array}{*{20}{c}} {{{\varvec{Q}}_a}{{{\dot{\varvec{\omega }}}}_{ae}}}\\ {{{\varvec{Q}}_p}{{{\dot{\varvec{\omega }}}}_{pe}}} \end{array}} \right] } \end{array} \end{aligned}$$
(37)

Theorem 2

 [24]. For the rotating appendages system (14),the system states coverge to zero in fixed time.

Proof

we consider the candidate Lyapunov function

$$\begin{aligned} {{\varvec{V}}_r} = \frac{1}{2}{\varvec{S}}_r^{\text{T}}{\varvec{J}}{{\varvec{S}}_r} \end{aligned}$$
(38)

Then we can obtain:

$$\begin{aligned} \begin{array}{*{20}{l}} {{\dot{{\varvec{V}}}_r}}&{} = &{}{{\varvec{S}}_r^{\text{T}}{{{\dot{\varvec{S}}}}_r}}\\ {}&{} = &{}{{\varvec{S}}_r^{\text{T}}\left\{ {{{{\dot{\varvec{\omega }}}}_{re}} + \frac{1}{2}{{\varvec{x}}_r}\left[ {{{\varvec{c}}_1}m{\varvec{q}}_{re}^{m - 1} + {{\varvec{c}}_2}n*\text{sig}{^{n - 1}}\left( {{{\varvec{q}}_{re}}} \right) } \right] {{{\dot{\varvec{q}}}}_{re}}} \right\} }\\ {}&{} = &{}{{\varvec{S}}_r^{\text{T}}\left\{ {\frac{1}{2}{{\varvec{x}}_r}\left[ {{{\varvec{c}}_1}m{\varvec{q}}_{re}^{m - 1} + {{\varvec{c}}_2}n*\text{sig}{^{n - 1}}\left( {{{\varvec{q}}_{re}}} \right) } \right] {{{\dot{\varvec{q}}}}_{re}}} \right\} }\\ {}&{}{}&{}{ + {\varvec{S}}_r^{\text{T}}\left\{ {\left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}}&{}0\\ 0&{}{\varvec{I}} \end{array}} \right] \left[ {\begin{array}{*{20}{l}} {{{\varvec{U}}_a}}\\ {{{\varvec{U}}_p}} \end{array}} \right] - \left[ {\begin{array}{*{20}{l}} {{\varvec{H}}_a^{\text{T}}}\\ {{\varvec{R}}_{sp}^{\text{T}}} \end{array}} \right] {{{\dot{\varvec{\omega }}}}_b} + \left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}{{\varvec{F}}_a}{\vartheta _\eta }}\\ {{{\varvec{T}}_c}} \end{array}} \right] } \right\} } \end{array} \end{aligned}$$
(39)

Substituting (37) into the formula(38) and it is organized as follows:

$$\begin{aligned} \begin{array}{*{20}{l}} {{\dot{{\varvec{V}}}_r}}&{} = &{}{{\varvec{S}}_r^{\text{T}}\left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}}&{}0\\ 0&{}{\varvec{I}} \end{array}} \right] \left\{ { - \frac{1}{4}{{\varvec{x}}_r}\left[ {{{\varvec{c}}_1}m{\varvec{q}}_{re}^{m - 1} + {{\varvec{c}}_2}n*\text{sig}{^{n - 1}}\left( {{{\varvec{q}}_{re}}} \right) } \right] \left[ {\begin{array}{*{20}{c}} {{{\varvec{Q}}_a}{{{\dot{\varvec{\omega }}}}_{ae}}}\\ {{{\varvec{Q}}_p}{{{\dot{\varvec{\omega }}}}_{pe}}} \end{array}} \right] } \right\} }\\ {}&{}{}&{}{ + {\varvec{S}}_r^{\text{T}}\left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}}&{}0\\ 0&{}{\varvec{I}} \end{array}} \right] \left\{ { - \left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}{{\varvec{F}}_a}{\vartheta _\eta }}\\ {{{\varvec{T}}_c}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{\varvec{J}}_a}{\varvec{H}}_a^{\text{T}}}\\ {{\varvec{R}}_{sp}^{\text{T}}} \end{array}} \right] {{\varvec{\omega }}_\gamma } - {{\left[ {{\tau _1}{{\varvec{S}}_r} + {\tau _2}\text{sat}{^{\text{T}}}\left( {{{\varvec{S}}_r}} \right) } \right] }^{0.5}}} \right\} }\\ {}&{}{}&{}{ + {\varvec{S}}_r^{\text{T}}\left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}}&{}0\\ 0&{}{\varvec{I}} \end{array}} \right] \left\{ {\frac{1}{2}{{\varvec{x}}_r}\left[ {{{\varvec{c}}_1}m{\varvec{q}}_{re}^{m - 1} + {{\varvec{c}}_2}n*\text{sig}{^{n - 1}}\left( {{{\varvec{q}}_{re}}} \right) } \right] {{{\dot{\varvec{q}}}}_{re}}} \right\} }\\ {}&{}{}&{}{ + {\varvec{S}}_r^{\text{T}}\left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}}&{}0\\ 0&{}{\varvec{I}} \end{array}} \right] \left\{ { - \left[ {\begin{array}{*{20}{c}} {{\varvec{H}}_a^{\text{T}}}\\ {{\varvec{R}}_{sp}^{\text{T}}} \end{array}} \right] {{{\dot{\varvec{\omega }}}}_b} + \left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}{{\varvec{F}}_a}{\vartheta _\eta }}\\ {{{\varvec{T}}_c}} \end{array}} \right] } \right\} }\\ {}&{} = &{}{{\varvec{S}}_r^{\text{T}}\left\{ { - \left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}}&{}0\\ 0&{}{\varvec{I}} \end{array}} \right] {{\left[ {{\tau _1}{{\varvec{S}}_r} + {\tau _2}\text{sat}{^{\text{T}}}\left( {{{\varvec{S}}_r}} \right) } \right] }^{0.5}} + \left[ {\begin{array}{*{20}{c}} {{\varvec{H}}_a^{\text{T}}}\\ {{\varvec{R}}_{sp}^{\text{T}}} \end{array}} \right] \left( {{{\varvec{\omega }}_\gamma } - {{{\dot{\varvec{\omega }}}}_b}} \right) } \right\} }\\ {}&{} \le &{}{ - {\varvec{S}}_r^{\text{T}}\left[ {\begin{array}{*{20}{c}} {{\varvec{J}}_a^{ - 1}}&{}0\\ 0&{}{\varvec{I}} \end{array}} \right] {{\left[ {{\tau _1}{{\varvec{S}}_r} + {\tau _2}\text{sat}{^{\text{T}}}\left( {{{\varvec{S}}_r}} \right) } \right] }^{0.5}}}\\ {}&{} \le &{}{ - {{\left[ {{\upsilon _1}{{\varvec{V}}_r} + {\upsilon _2}{\varvec{V}}_r^{t'}} \right] }^{0.5}}} \end{array} \end{aligned}$$

where \({\upsilon _1} = \min \left\{ {{{ {{J_a}} \big |}_{\min }}{{ {{\tau _1}} \big |}_{\min }},{{ {{\tau _1}} \big |}_{\min }}} \right\}\) and \({\upsilon _2} = \min \left\{ {{{ {{J_a}} \big |}_{\min }}{{ {{\tau _2}} \big |}_{\min }},{{ {{\tau _2}} \big |}_{\min }}} \right\}\).it is easy known:

$$\begin{aligned} {{\dot{\varvec{V}}}_r} + {\left[ {{\upsilon _1}{{\varvec{V}}_r} + {\upsilon _2}{\varvec{V}}_r^{t'}} \right] ^{0.5}} \le 0 \end{aligned}$$
(40)

According to Lemma 1, the convergence time can be determined as:

$$\begin{aligned} T \le \frac{2}{{\upsilon _{_1}^{0.5}}} + \frac{1}{{\upsilon _{_2}^{0.5}\left( t'\big / 2 - 1 \right) }} \end{aligned}$$
(41)

\(\square\)

4 Numerical Simulation Results

This paper mainly focuses on the attitude control of a new type of rotating satellites. This section presents the numerical simulations demonstrating the performance of the proposed controller. The results of the proposed method are compared with FSM and PD controller. In the numerical simulation. the parameters of the spacecraft platform, flexible solar panels, magnetic bearing, and rotating payload are same as references [41].

In this analysis, the inertia matrix of the spacecraft platform \({{\varvec{I}}_{b0}}= \text{diag}(3538.75,2612.73,4402.37)\) \(\mathrm{{kg}} \cdot {\mathrm{{m}}^2}\) and the initial angular velocity of the platform is \({{\varvec{\omega }}_{b0}} = {\left[ {\begin{array}{*{20}{c}} {{{0}}{{.035}}}&{{{ - 0}}{{.012}}}&{{{0}}{{.025}}} \end{array}} \right] ^{\text{T}}}\) \(\mathrm{{rad/s}}\). The inertia matrix of the flexible solar panel is \({{\varvec{I}}_a} = \text{diag}(290.15,187.32,203.89)\) \(\mathrm{{kg}} \cdot {\mathrm{{m}}^2}\) and the desire angular velocity of it relative to the platform is \({{\varvec{\omega }}_{ad}} = \left[ {0;0.2;0} \right]\) \(\mathrm{{rad/s}}\). \({{\varvec{I}}_p} = \text{diag}(251.78,0.79,0;0.79,15.76,0.32;0,0.32,11.46)\) \(\mathrm{{kg}} \cdot {\mathrm{{m}}^2}\)indicates the inertia matrix of the rotating rigid payload and the desired angular velocity of the payload is \({{\varvec{\omega }}_{pd}} = \left[ {0.28;0;0} \right]\) \(\mathrm{{rad/s}}\). The external disturbance torque, which includes constant disturbance and period disturbance, is described as \({\varvec{d}} = [\sin (0.5\pi t) + 1.5;\sin (0.5\pi t) + 1.5;\sin (0.5\pi t) + 1.5]\). The parameters of the controller are selected as follows:

$$\begin{aligned} \begin{array}{l} {{\varvec{k}}_1} = \text{diag}(300,320,310,),{{\varvec{k}}_2} = \text{diag}(180,180,180),\\ {{\varvec{c}}_1} = \text{diag}(120,120,120,100,100,100),{{\varvec{c}}_2} = \text{diag}(80,80,80,50,50,50),\\ \alpha = {9 / {11}},m = 1.5,n = 3,{k_{\text{in}}} = 100,{k_{\text{out}}} = 0.5\\ E = \left[ {1,0,0,0;,0,1,0,0; - 1, - 1,0,\sqrt{3}/3} \right] , {\varvec{\sigma }} = \text{diag}\left[ {0.8,1,0,1} \right] \end{array} \end{aligned}$$
(42)
Fig. 4
figure 4

error angular velocity and error quaternion variation of spacecraft platform

Full size image
Fig. 5
figure 5

error angular velocity and error quaternion variation of flexible solar panels

Full size image

The results of the attitude angular velocity and the vector of the error quaternion of the platform are presented in Fig. 4. Similarly, the trend of the attitude angular velocity error and the error quaternion of the flexible solar panels relative to the Y-axis of the spacecraft platform are shown Fig. 5.

Fig. 6
figure 6

error angular velocity and error quaternion variation of rotating payload

Full size image
Fig. 7
figure 7

Output torque of platform actuators

Full size image

Figure 6 show the results of the attitude angular velocity error and the error quaternion of the rotating payload relative to the X-axis of the spacecraft platform. Figure 7 shows the variation trend of the output torque of actuator. The X-axis actuator is reduced to 80\(\%\) of the maximum output torque and the Z-axis actuator completely fails. From Figs. 4, 6 and 7,we can know that every part of the spacecraft system can reach their desired states quickly. The angular velocity and quaternion errors of the spacecraft system which converge to the stable state is less than theoretical time. The convergence time of the spacecraft platform, flexible solar panels and payload under the AFS control law are respectively about 45s, 40s and 25s. It shows that the control law proposed in this paper make the components of spacecraft system converge to the equilibrium position and can illustrate the law is useful and effective even the actuator failures occur during operation.

Fig. 8
figure 8

Comparisons of spacecraft platform error angular velocity and error quaternion

Full size image
Fig. 9
figure 9

Comparisons of flexible solar panels error angular velocity and error quaternion

Full size image
Fig. 10
figure 10

Comparisons of rotating payload error angular velocity and error quaternion

Full size image

Figure 8 show the trend of angular velocity and quaternion errors of the spacecraft platform which were obtained by different control schemes, the control law proposed in this paper obviously takes less time than other schemes even if they can converge to the equilibrium position from those figures. Figure 9 shows trend of the angular velocity error and quaternion error of the flexible solar panels relative to the y-axis rotation of the spacecraft platform under different control laws. The convergence time of different control methods is similar and they can guarantee the flexible solar panels reaching stable state even if it rotating and vibrating. Figure 10 show the angular velocity error and quaternion error of the rotating payload from the static state to the stable state under different control laws. These figures mainly show the comparisons between the proposed AFS, the finite-time sliding mode (denoted as FSM) and the PD control law. The proposed law can firstly make the payload reach the stable state. The rotating payload is affected by the dynamic and static imbalance will produce a stable gyro effect from Fig. 6 and Fig. 10.

Table 1 The convergence time under different control laws
Full size table
Table 2 The stability accuracy level of each component under different control laws
Full size table

Table 1 shows the adjustment time required for each component to reach the desired state under different control laws, and Table 2 shows the stability accuracy level of each component of the spacecraft under different control laws. It can be clearly seen from the table that the control law proposed in this paper is obviously better than other control laws, and its stability accuracy is higher than other control laws. From the pictures and tables, the adaptive law proposed in this paper can effectively suppress the vibration of the spacecraft flexible solar panel, while other control laws are not robust enough to the vibration of the spacecraft flexible solar panel. The desired steady state of the rotating payload is the fastest to be brought under the fixed-time sliding mode control law proposed in this paper, while it is slower the other two control laws.Therefore, it can be concluded that the proposed AFS law has advantage in fast convergence and robustness than other control schemes for models are considered in this study.

5 Conclusion

A spacecraft with a rotating payload and rotating flexible solar panels have been established in this study. We have proposed corresponding control schemes to realize the rotation of the payload and flexible solar panels relative to the spacecraft platform at a predefined angular velocity. To achieve fast convergence and accurate tracking performance in the presence of various disturbances and actuator faults, we have put forward an adaptive fuzzy sliding mode for spacecraft platform and fixed-time sliding mode control strategy for the rotating appendages. Then, the numerical simulations have been used to demonstrate the attitude of the spacecraft system converged to stable state via the proposed algorithms. Hence, we hope the proposed control schemes can contribute to the future space explorations and can be used in actual engineering application for the future work. In practical situations, there are some points which are not addressed in this paper. As a future perspective for this work, we suggest the investigation into the case where inherent nonholonomic constraints on actuator can be considered.