A New Picture Fuzzy Entropy and Its Application Based on Combined Picture Fuzzy Methodology with Partial Weight Information

Abstract

Picture fuzzy set (PFS) is more comprehensive tool than intuitionistic fuzzy set (IFS) for modeling the uncertain decision-making problems. In this paper, a new picture fuzzy entropy measure is proposed and proved that the proposed measure satisfies the axiomatic definition of entropy measures for picture fuzzy sets. Besides this, the useful mathematical properties of the new entropy measure are also investigated. The justification of the proposed picture fuzzy measure is established by discussing its particular cases and compares it with the existing entropy measures. Then, for the case where criteria weights are partially known, we used an entropy-based method to produce objective weights. For the uncertain environment, TODIM (portuguese acronym for interactive multicriteria decision-making) and ELECTRE methods are useful for practical problems. Based on the advantages of PFSs,TODIM, and ELECTRE, we proposed an integrated picture fuzzy TODIM-ELECTRE to combine the prominent benefits of these theories. We present the TODIM-ELECTRE model for PFS environment and express the computing steps in brief of this new established model. Thereafter, the superiority of the new model is verified by a numerical example of supplier selection and through comparative study with other existing methods.

1 Introduction

To address the information uncertainty in a better manner, fuzzy set (FS) theory developed by Zadeh [1] in decision-making issues which represents the uncertain information by the membership degree. Researchers have been started thinking for fuzzy theories and posed some important theories, for example, generalized fuzzy set theory [1,2,3], intuitionistic fuzzy set (IFS) theory [4, 5], hesitant fuzzy set theory [6, 7], rough set theory [8,9,10], and so forth various direct/indirect expansions of the notion of fuzzy set (FS) are created and successfully connected within the overwhelming majority of the problems in real-life situation. A significant modification of FS is proposed by Atanassov [4] named as intuitionistic FS. IFS theory proved very intensive as well as significant because it is characterized by membership degree ($\rho \in [0,1]$) and non-membership degree ($\eta \in [0,1]$) on the condition that the sum of their aggregate hold with $\rho +\eta \le 1.$ The introduction of third component with the name of “intuitionistic index ($\phi$)” thus satisfies $\rho +\eta +\phi =1.$

It is seen that FSs are IFSs; however, converse may not be true. IFS has been broadly used to modeled with the practical applications in different fields. Xu and Yager [11] suggested some geometric averaging operator to aggregate the different intuitionistic fuzzy values (IFVs). However, an IFS is a powerful tool in expressing vague and uncertainty of decision problems. Some prominent applications of intuitionistic FSs can be found in decision-making [12,13,14,15,16,17], medical diagnosis [18, 19], and pattern recognition [19, 20]. IFSs lack a key concept, i.e., neutral degree, which has an important role in diverse situations such as personal selection, human voting, and medical diagnosis, which may limit their applications. Recently, Singh and Ganie [21] discussed some scenarios in our day-to-day life that are difficult to assess using intuitionistic fuzzy set theory.

The picture fuzzy set (PFS), a general characterization of Zadeh’s fuzzy set [1, 22], and IFS [4] have been suggested by Cuong [23, 24]. Essentially, picture fuzzy models are used in most real-life problems requiring human opinions including most answer types: yes, abstain, no, and refusal. The main parts of the PFS are positive membership $(\rho )$ , neutral membership $( \nu )$, negative membership $(\eta )$ , and refusal membership $(\phi )$ , respectively, and sum of all membership degrees must not exceed 1. It is noted that the refusal membership degree ( index of hesitancy) of PFS is not an independent parameter. If a decision-maker is asked to comment on any statement, the positive of the statement is 0.5, neutrality is 0.3, and negative degree is 0.1. In picture fuzzy environment, it is described as (0.5, 0.3, 0.1,0.1). In the picture FS theory, linguistic terms are tools that use picture fuzzy sets to describe linguistic expression, mathematically. As expressing imprecise, uncertainty, incomplete, and inconsistent information with the PFNs is easier in MCDM (multicriteria decision-making) problems. Cuong [23] studied some operations and properties of PFSs and developed distance measures between PFSs. Some researchers have been studied the problems under the PFSs environment. Development of picture FS has a new parameter, the neutral function which solves the complex problems in a better manner. The construct of PFSs has been utilized for modeling various real-life decision-making problems with the help of different tools like similarity measure and distance measures, among others [7, 25,26,27,28, 25,26,27,28].

2 Related Work

Recently, various authors applied PFSs in clustering analysis, cleaner production, decision-making, and problems; for example, Zhang et al. [30] proposed some aggregation operators on PFSs, Wei [7] proposed cross-entropy for PFSs and applied it in decision-making, Wang et al. [32] introduced picture fuzzy normalized projection-based VIKOR method and applied it in risk evaluation for construction project, Wei [33] proposed similarity measures for PFSs, and Nie et al. [25] investigated a voting method based on 2-tuple linguistic picture preference relation, etc. Peng and Dai [26] developed an algorithm for picture fuzzy multiple attribute decision-making based on new distance measure. A generalized picture distance for picture fuzzy clustering was proposed by Son [31]. Arya and Kumar [34] proposed a picture fuzzy entropy with its application in opinions polls. Joshi [27, 28] suggested some comparison/compatibility measures for picture fuzzy framework. Kadian and Kumar [29] proposed a novel picture fuzzy divergence measure with its application for COVID-19 and pattern recognition. For MCDM problems in PF environment, Luo and Liang [35] proposed a hybrid TODIM approach with unknown weight information for the performance evaluation of cleaner production. An innovative correlation coefficient with its application in pattern recognition was given by Singh and Ganie [21].

The amount of entropy is closely linked to fuzziness index of FS and is very important for uncertain measure in decision-making. De Luca and Termini [36] studied that Shannon entropy could be utilized for measuring the information amount and gave an axiomatic definition entropy for FS. Entropy is related to the information considering the useful context for FSs. Subsequently, various researchers introduced various entropy measures for FSs [2, 37,38,39,40]. Next, based on Havrda-Charvat [57] entropy, Hung and Yang [41] proposed another axiomatic construction entropy for Atanassov IFSs. Similar to FSs, entropy for intuitionistic FSs has been developed by different eminent authors [13,14,15,16, 13,14,15,16] and the results have been implemented in medical diagnosis, pattern recognition, supplier selection, image segmentation, and real-life decision-making problems. Chatterjee [44] discussed the foremost problem in uncertainty which exists for patenting. However, we discover that less research has been done in the entropy domain for PFSs. Therefore, this article focuses on entropy information of PFSs which includes the four components of PFSs.

Multicriteria decision-making (MCDM) domain is one within which we want to select the most appropriate alternative from a finite set of alternatives and the aim is achieve a preferable alternative that satisfy an explicit set of conflicting criteria. The criterion is thus conflicting as well as equivalent that it turns out to be very tedious task to decide an optimal decision, for instance buying a car or purchasing a house etc., are some familiar real- world activities of decision-making problems. TODIM method has a better description to model with decision-making problems, proposed by Hwang and Yoon [45]. Over the past years, TODIM has been applied in untold practical domains especially in business problems, medical sciences, decision problems, social sciences, engineering, etc. [25, 46,47,48,49,50]. ELECTRE method is known as comprehensive evaluation approach and its derivatives play an active role in MCDM problems. The ELECTRE method was first proposed by Benayoun et al. [51], which is based upon the pseudocriteria and outranking relations.

Furthermore, numerous authors have developed many techniques for solving MCDM issues, for example, VIKOR [52], PROMETHEE [45, 53], and so forth. Recently, Arya and Kumar [34, 54] combined TODIM and VIKOR methods skillfully and implemented them to the picture fuzzy environment. Xu et al. [55] implemented the integration of TODIM and PROMETHEE method under single-valued neutrosophic environment. This pattern of integrating the TODIM method with another technique realizes to have been a recent trend among researchers. For the uncertain environment, TODIM and ELECTRE methods are useful for practical problems and widely used in fuzzy environment. Therefore, to obtain comprehensive ranking results, combining the entropy weight method, TODIM and ELECTRE methods may be a good choice. The aim of presented article is to build an enlarged TODIM-ELECTRE model with the original TODIM and ELECTRE methods and PF information to settle with MCDM problems more effectively. Based on the advantages of PFSs, TODIM, and ELECTRE, we proposed picture fuzzy (PF) TODIM-ELECTRE to combine the prominent benefits of these theories.

The main innovations and contributions are as follows:

• First, original decision-making information is represented by PFNs (for fuzzy evaluation information under qualitative criteria).

• Second, we develop the picture fuzzy entropy for picture fuzzy information, which can help to find the partial weights information of the criteria.

• Third, we develop an algorithm to deal with multicriteria decision-making problems using picture fuzzy information and the traditional TODIM approach is integrated with ELECTRE to obtain ranking results of alternatives. Consequently, the developed approach can model the higher degrees of uncertainty in a more efficient way.

• Fourth, to show the reliability and effectiveness of the proposed PF TODIM-ELECTRE approach, the presented MCDM method is applied in evaluating the best partner for footwear company. Its superiorities and feasibility are also certified with detailed comparative analyses with some existing studies.

The presence paper is organized as follows: Section 1 describes some introduction concepts of FS, IFS, and PFS. In Sect. 3, first the existing literature related to proposed work is looked into and afterward, another new framework for PFSs is discussed. Also, a new entropy measure for PFS is introduced and validated it. Section 3 compares the proposed entropy measure with the existing entropy measures. Section 4 gives comprehensive details about the proposed integrated TODIM-ELECTRE method. In Sect. 5, the practically of the integrated method is explained through an example on selection problem where the scheme for weight vector is partially known and a comparative discussion with the existing studies is demonstrated. In the last section, the manuscript is presented with conclusion and future research agenda.

3 Theoretical Background

In this section, some needed basic definitions and important concepts like FS, IFS, and picture FS have demonstrated over the universal set $\Game =\{\tilde{t_1},\tilde{t_2}, \ldots,\tilde{t_n}\}.$

Definition 2.1

(Zadeh [1]). A FS (E) on a universal set $\Game$ is given as:

$$\begin{aligned} E=\left\{ \left( \tilde{t_i},\rho _{E}( \tilde{t_i}) \right): \tilde{t_i}\in \Game \right\} , \end{aligned}$$

(1)

where $\rho _{E}: \Game \rightarrow [0,1]$ signifies the membership grade of each element $\tilde{t_i}\in \Game$.

Definition 2.2

(Atanassov [4]) An IFS (E) on a universal set $\Game$ is given as:

$$\begin{aligned} E=\left\{ \left( \tilde{t_i},\rho _E( \tilde{t_i}),\eta _{E}( \tilde{t_i}) \right):\tilde{t_i}\in \Game \right\} , \end{aligned}$$

(2)

where

$$\begin{aligned} \rho _{E}:\Game \rightarrow [0,1]\; \text {and}\; \eta _{E} :\Game \rightarrow [0,1], \end{aligned}$$

with $0\le \rho _{E}(\tilde{t_i})+\eta _{E}(\tilde{t_i})\le 1,$ for each $\tilde{t_i}\in \Game .$

For any IFS E in $\Game$, the number $\phi _{E}(\tilde{t_i})\in [0,1]=1-\rho _{E}( \tilde{t_i})-\eta _{E}( \tilde{t_i}), \tilde{t_i}\in \Game$ is the hesitancy degree of $\tilde{t_i}$ in $\Game$. Further, $\phi _{E}( \tilde{t_i})$ is called intuitionistic FS index. Obviously, when $E=\phi _{E}(\tilde{t_i})=\eta _{E}(\tilde{t_i})$, IFS E alters an ordinary FS.

3.1 PFS and Its Properties

Cuong [23] developed classical intuitionistic fuzzy set to the PFS by adding neutral degree. A PFS is described as:

$$\begin{aligned} E=\left\{ \left( \tilde{t_i},\rho _E(\tilde{t_i}),\nu _{E}(\tilde{t_i}),\eta _E( \tilde{t_i}) \right): \tilde{t_i}\in \Game \right\} \end{aligned}$$

(3)

which is defined with positive ($\rho _{E}$), neutral ($\nu _{E}$), and negative ($\eta _E$) membership degrees, where

$$\begin{aligned} \rho _{E} :\Game \rightarrow [0,1], \tilde{t_i} \in \Game \rightarrow \rho _E(\tilde{t_i})\in [0,1], \\ \nu _{E} :\Game \rightarrow [0,1], \tilde{t_i} \in \Game \rightarrow \nu _E(\tilde{t_i})\in [0,1], \\ \eta _{E} :\Game \rightarrow [0,1], \tilde{t_i} \in \Game \rightarrow \eta _E(\tilde{t_i})\in [0,1], \end{aligned}$$

with the condition

$$\begin{aligned} 0\le \rho _{E}(\tilde{t_i})+\nu _{E}(\tilde{t_i})+\eta _{E}(\tilde{t_i})\le 1 \;{\text {for\, all}}\; \tilde{t_i}\in \Game . \end{aligned}$$

The fourth parameter of PFS is $\phi _{E}(\tilde{t_i})$, regarded as the picture fuzzy index as:

$$\begin{aligned} \phi _{E}(\tilde{t_i})=1-\rho _{E}( \tilde{t_i})-\nu _{E}( \tilde{t_i})-\eta _E( \tilde{t_i}). \end{aligned}$$

and

$$\begin{aligned} 0 \le \phi _{E}(\tilde{t_i}) \le 1. \end{aligned}$$

For convenience, the pair $E=(\rho _{E}(\tilde{t_i}),\nu _{E}(\tilde{t_i}),\eta _E( \tilde{t_i}),\phi _E(\tilde{t_i}))$ is named a PFN (picture fuzzy number) or PF value and every PF value is denoted by $\beta =(\rho _{\beta },\nu _{\beta },\eta _{\beta },\phi _{\beta }),$ where $\rho _{\beta }\in [0,1],\nu _{\beta }\in [0,1],\eta _{\beta }\in [0,1],\nu _{\beta }\in [0,1],\phi _{\beta } \in [0,1]$ and $\rho _{\beta }+\nu _{\beta }+\eta _{\beta }+\phi _{\beta }= 1.$ Sometimes, we omit $\phi _{\beta }$ and in short, we denote a PFN as $\beta =(\rho _{\beta },\nu _{\beta },\eta _{\beta }).$

Definition 2.3

For every two PFSs E and F, Cuong and Kreinovich [56] defined some operations in the universe $\Game$ as follows:

• 1. $E \subseteq F$ iff $\forall \tilde{t_i}\in \Game$, $\rho _E( \tilde{t_i})\le \rho _F( \tilde{t_i}),\nu _E(\tilde{t_i})\le \nu _F( \tilde{t_i}),\eta _E(\tilde{t_i})\ge \eta _F(\tilde{t_i})$ ;

• 2. $E=F$ iff $\forall \tilde{t_i}\in \Game ,$ $E\subseteq F$ and $F\subseteq E$;

• 3. $E\cap F=\{\rho _E( \tilde{t_i})\wedge \rho _F(\tilde{t_i})\;, \; \nu _E( \tilde{t_i})\wedge \rho _F(\tilde{t_i})\;, \mathrm {and}\; \eta _E(\tilde{t_i}) \vee \eta _F( \tilde{t_i})| \tilde{t_i}\in \Game \}$;

• 4. $E\cup F=\{\rho _E( \tilde{t_i})\vee \rho _F(\tilde{t_i}),\; \nu _E( \tilde{t_i})\wedge \rho _F(\tilde{t_i}),\; \mathrm {and}\; \eta _E(\tilde{t_i}) \wedge \eta _F( \tilde{t_i})| \tilde{t_i}\in \Game \}$.

• 5. If $E\subseteq F$ and $F\subseteq P$, then $E\subseteq P$;

• 6. $(E^{c})^c=E;$

• 7. coE= $E^{c}=\{\left( \tilde{t_i},\eta _E(\tilde{t_i}),\nu _E( \tilde{t_i}),\rho _E( \tilde{t_i})| \tilde{t_i}\in \Game \right) \}$.

Definition 2.4

[32] Let $\beta _1=(\rho _{\beta _1},\nu _{\beta _1},\eta _{\beta _1})$ and $\beta _2=(\rho _{\beta _2},\nu _{\beta _2},\eta _{\beta _2})$ be two PFNs. $H(\beta _i)=\rho _{\beta _i}+\nu _{\beta _i}+\eta _{\beta _i}(i=1,2)$ be the accuracy degree and score$(\beta _i)=\rho _{\beta _i}- \eta _{\beta _i}(i=1,2)$ be the score function values of $\beta _1$ and $\beta _2,$ , respectively. Then:

• If $score(\beta _1)< score(\beta _2)$, then $\beta _1 < \beta _2$;

• If $score(\beta _1)= score(\beta _2)$, then

  • (a). If $H(\beta _1)< H(\beta _2)$, implies that $\beta _2$ is superior to $\beta _1$ , denoted by $\beta _1<\beta _2.$

  • (b). If $H(\beta _1) =H(\beta _2),$ implies that $\beta _1$ is equivalent to $\beta _2,$ denoted by $\beta _1 \equiv \beta _2$.

Definition 2.5

Wang et al. [32] introduced the following relations for PFNs $\beta _1=(\rho _{\beta _1},\nu _{\beta _1},\eta _{\beta _1})$, $\beta _2=(\rho _{\beta _2},\nu _{\beta _2},\eta _{\beta _2})$.

• (1). $\beta _1 \otimes \beta _2=(\rho _{\beta _1}+\nu _{\beta _1})(\rho _{\beta _2}+\nu _{\beta _2})-\nu _{\beta _1}\nu _{\beta _2},\nu _{\beta _1}\nu _{\beta _2},1-(1-\eta _{\beta _1})(1-\eta _{\beta _2});$

• (2). $\beta _{1}^{n}=(\rho _{\beta _1}+\nu _{\beta _1})^n-\nu _{\beta _1}^{n},\nu _{\beta _1}^{n},1-(1-\eta _{\beta _1})^{n} \;\mathrm {for}\;n > 0.$

Definition 2.6

Suppose $\beta _1=(\rho _{\beta _1},\nu _{\beta _1},\eta _{\beta _1})$ and $\beta _2=(\rho _{\beta _2},\nu _{\beta _2},\eta _{\beta _2})$ be two PFNs. The generalized distance of PFNs is defined by Zhang et al. [30] and can be characterized as below:

$$\begin{aligned}&d_H(\beta _1,\beta _2)=\left( \frac{1}{5}\left( \left| \rho _{\beta _1}-\rho _{\beta _2}\right| ^{\lambda }+\left| \eta _{\beta _1}-\eta _{\beta _2}\right| ^{\lambda }\right. \right. \nonumber \\&\quad \left. \left. +\left| \nu _{\beta _1}-\nu _{\beta _2}\right| ^{\lambda }+\left| \text {max}\{\rho _{\beta _1},\eta _{\beta _2}\} -\text {max}\{\eta _{\beta _1},\rho _{\beta _2}\}\right| ^{\lambda }\right. \right. \end{aligned}$$

(4)

$$\begin{aligned}&\left. \left. +\left| \text {max}\{\rho _{\beta _1},\nu _{\beta _2}\} -\text {max}\{\nu _{\beta _1},\rho _{\beta _2}\}\right| ^{\lambda } \right) \right) ^\frac{1}{\lambda } (\lambda >0). \end{aligned}$$

(5)

4 History of Fuzzy Measures

Let $\Theta _n=\{\Game =(\tilde{t_1},\tilde{t_2}, \ldots,\tilde{t_n}): \tilde{t_i}\ge 0,\sum _{i=1}^{n} \tilde{t_i}=1\}, n\ge 2$ be a finite set of complete probability distribution. For any $\Game =(\tilde{t_1},\tilde{t_2}, \ldots,\tilde{t_n})\in \Theta _n,$ , Havrda and Charavat’s [57] studied the information measure of the probability distribution for a given positive real number $\sigma$ and known as one parametric extension of Shannon entropy [58]. The specific mathematical form of Havrda and Charavat’s [57] is given below:

$$\begin{aligned} V^{HC}_{\sigma }(\Game )=\frac{1}{(2^{1-\sigma }-1)}\left[ 1- \sum _{i=1}^{n}\tilde{t_i}^{\sigma } \right] , \qquad \sigma >0(\ne 1). \end{aligned}$$

(6)

Further, the generalization of Shannon entropy [58] was proposed by Tsallis [59] by introducing a parameter and is given by:

$$\begin{aligned} V^{Ts}_{\sigma }(\Game )=\frac{1}{(\sigma -1)}\left[ 1- \sum _{i=1}^{n}\tilde{t_i}^{\sigma } \right] , \qquad \sigma >0(\ne 1). \end{aligned}$$

(7)

Shannon entropy [58] is the limiting case of Havrda and Charavat’s [57] and Tsallis entropy [59] as $\sigma \rightarrow 1$. The only difference between Tsallis entropy [59] and Havrda–Charvat entropy [57] is a normalizing factor. At $\Game =\left( \frac{1}{2},\frac{1}{2} \right) ,$ Havrda–Charvat entropy reduces to one whereas Tsallis entropy does not reduce to one. In other words, we can say that Havrda–Charvat entropy is normalized whereas Tsallis entropy is not normalized.

Recently, Arya and Kumar [37] extended it from another aspect as follows:

$$\begin{aligned} V_{\sigma }(\Game )=\frac{1}{(\sigma -\sigma ^{-1})}\left[ \sum _{i=1}^{n}({\tilde{t_i}}^{\sigma ^{-1}}-{\tilde{t_i}}^{\sigma } \right] \end{aligned}$$

(8)

where $\sigma >0(\ne 1).$

If $\sigma \rightarrow 1$, (8) recovers the Shannon [58] entropy. After that, Arya and Kumar [37] extended $\sigma$ information measure to different aspects and they applied it in FSs. Let $X=\{q_1,q_2, \ldots,q_n\}$ denote the universe of discourse and the FS is $M=\{(q_i, u_M(q_i))|\;q_i\in X\}$. Arya and Kumar [37] modified the following fuzzy information measure as follows:

$$\begin{aligned} \begin{aligned}&F\;V_\sigma (E)\\&=\frac{1}{n\left( \sigma -\sigma ^{-1}\right) } \sum _{i=1}^{n}\left[ ( \rho _E(\tilde{t_i}))^{\sigma ^{-1}}+(1- \rho _E(\tilde{t_i}))^{\sigma ^{-1}} \right. \\&\quad \left. -( \rho _E(\tilde{t_i}))^\sigma + (1- \rho _E(\tilde{t_i}))^\sigma \right] . \end{aligned} \end{aligned}$$

(9)

Bhandari and Pal [39] generalized the information measure for FSs that was proposed by Hung and Yang [41]. They proposed two families of information measure for IFSs. Let the finite universe of discourse be $\{\Game =\tilde{t_1},\tilde{t_2}, \ldots,\tilde{t_n}\}$ and an IFS $F=\{(\tilde{t_i},\rho _M(\tilde{t_i}),\nu _E)(\tilde{t_i})|\;\tilde{t_1}_i\in \Game \}$, the two forms of $IF\;V_\sigma (F)$ are as follows:

$$IF\;V_\sigma (F)=\frac{1}{n(1-\sigma )}\sum _{i=1}^{n}[\rho _F( {\tilde{t_i}})^{\sigma }+\nu _E({\tilde{t_i}})^{\sigma } +\phi _E({\tilde{t_i}})^{\sigma }-1], \mathrm {where} \; \sigma \in (0,1);$$

(10)

and

$$IF\;V_\sigma (F)=\frac{1}{n(1-\sigma )}\sum _{i=1}^{n}[\rho _F( {\tilde{t_i}})log_2({\tilde{t_i}}) +\nu _E({\tilde{t_i}})log_2({\tilde{t_i}})+\phi _E({\tilde{t_i}})log_2({\tilde{t_i}})], \mathrm {where} \; \sigma \in (0,1).$$

(11)

Further, the modified version of Hung and Yang [41] information measure proposed by Arya and Kumar [12] is given as follows:

$$V^{IFS}_{\sigma }(F)= \frac{1}{n (\sigma -\sigma ^{-1})}\sum _{i=1}^{n}\bigg [\bigg ( \rho _F(\tilde{t_i})^{\sigma ^{-1}}+\eta _F(\tilde{t_i})^{\sigma ^{-1}}+\phi _F(\tilde{t_i})^{\sigma ^{-1}}\bigg ) -\bigg ( \rho _F(\tilde{t_i})^{\sigma }+\eta _F(\tilde{t_i})^{\sigma }+\phi _F(\tilde{t_i})^{\sigma } \bigg ) \bigg ];$$

(12)

where $\sigma >0(\ne 1)$, $\rho _F(\tilde{t_i})$ is the degree of membership, $\eta _F(\tilde{t_i})$ is the degree of non-membership, $\phi _F(\tilde{t_i})$ is the degree of hesitancy, respectively, and $\phi _F(\tilde{t_i})=1-\rho _F(\tilde{t_i})-\eta _F(\tilde{t_i}), i=1,2,\ldots n$.

Keeping these generalizations in entropy theory, we present a new entropy of PFSs. First, let us give an axiomatic definition of the entropy for PFSs.

Definition 3.1

For any $E \in PFS(\Game )$, a real function $en:PFSs(\Game )\rightarrow [0,\infty )$ is an entropy for PFSs if En(E) holds the following requirements:

(P1)::

$en(E)=0$ $\Leftrightarrow$ E is a crisp set.

(P2)::

$en(E)=1$, that is, captures maximum value $\Leftrightarrow$ $\rho _{en}(\tilde{t_i})=\nu _{en}(\tilde{t_i})=\eta _{en}(\tilde{t_i})=\phi _{en}(\tilde{t_i})=\frac{1}{4},$ for all $\tilde{t_i}\in \Game .$

(P3)::

$en(E)=en(E^c),$ where $E^c$ is the complement of E.

(P4)::

$en(E)\le en(F)$ if E is less fuzzy than F, that is $\rho _{E}\le \rho _{F} ,\nu _{E}\le \nu _{F}$ and $\eta _E \le \eta _F$ for max $(\rho _{F},\nu _{F},\eta _{F})\le \frac{1}{4}$ and $\rho _{E}\ge \rho _{F}, \nu _{E}\ge \nu _{F}$ and $\eta _E \ge \eta _F$ for min $(\rho _{F},\nu _{F},\eta _{F})\ge \frac{1}{4}.$

We shall introduce a parametric information measure for PFSs in the next subsection and prove that it is an entropy measure satisfying Definition 3.1.

4.1 A Parametric Information Measure for PFSs

For any $E\in PFSs,$ we define

$$V^{PFS}_{\sigma }(E)= \frac{1}{n(\sigma -\sigma ^{-1})}\sum _{i=1}^{n} \bigg [( \rho _E( \tilde{t_i})^{\sigma ^{-1}}+\nu _E( \tilde{t_i})^{\sigma ^{-1}}+\eta _E( \tilde{t_i})^{\sigma ^{-1}}+\phi _E(\tilde{t_i})^{\sigma ^{-1}} ) - (\rho _E(\tilde{t_i})^{\sigma }+\nu _E(\tilde{t_i})^{\sigma }+\eta _E( \tilde{t_i})^{\sigma }+\phi _E(\tilde{t_i})^{\sigma } ) \bigg ].$$

(13)

where $\sigma >0(\ne 1)$, $\rho _E(\tilde{t_i})$ is the degree of membership, $\eta _E(\tilde{t_i})$ is the degree of neutral, $\nu _E(q_i)$ is the degree of non-membership, $\phi _E(\tilde{t_i})$ is the degree of hesitancy, respectively, and $\phi _E(\tilde{t_i})=1-\rho _E(\tilde{t_i})-\nu _E(\tilde{t_i})-\eta _E(\tilde{t_i}), i=1,2,\ldots n$. Particular Cases:

• 1. If $\sigma =1,$ then (13) becomes an extension of Hung and Yang [41] IF entropy for picture fuzzy set as :

  $$V^{PFS}_{\sigma }(E)={} -\frac{1}{n}\sum _{i=1}^{n}[\rho _E(\tilde{t_i})\log _2(\rho _E( \tilde{t_i})) +\nu _E(\tilde{t_i})\log _2(\nu _E(\tilde{t_i}))+\eta _E( \tilde{t_i})\log _2(\eta _E( \tilde{t_i})) +\phi _E(\tilde{t_i})\log _2(\phi _E(\tilde{t_i}))].$$

  (14)

• 2. If $\sigma =1$ and $\nu _{E}(\tilde{t_i})=0$, then (13) becomes Hung and Yang [41] entropy .

• 3. If $\nu _{E}( \tilde{t_i})=0$ (neutral degree), then proposed entropy alters into an IF entropy studied by Arya and Kumar [12]:

  $$i.e., V^{PFS}_{\sigma }(E)= {} \frac{1}{n(\sigma -\sigma ^{-1})} \sum _{i=1}^{n}[( \rho _E( \tilde{t_i})^{\sigma ^{-1}}+\eta _E(\tilde{t_i})^{\sigma ^{-1}}+\phi _E( \tilde{t_i})^{\sigma ^{-1}} ) - (\rho _E(\tilde{t_i})^{\sigma }+\eta _E( \tilde{t_i})^{\sigma }+\phi _E( \tilde{t_i})^{\sigma } ) ] .$$

  (15)

• 4. If $\eta _E(\tilde{t_i})=0,\phi _{E}(\tilde{t_i})=0$, then (13) recovers the fuzzy entropy:

  $$V^{PFS}_{\sigma }(E)= \frac{1}{n(\sigma -\sigma ^{-1})}\sum _{i=1}^{n}[( \rho _E( \tilde{t_i})^{\sigma ^{-1}}+(1-\rho _E( \tilde{t_i}))^{\sigma ^{-1}} - (\rho _E( \tilde{t_i})^{\sigma }+(1-\rho _E(\tilde{t_i})^{\sigma } ] .$$

  (16)

  where $\sigma >0(\ne 1)$ .

• 5. If $\eta _E( \tilde{t_i})=0,$ $\phi _{E}( \tilde{t_i})=0$ and $\sigma = 1$ , then (13) recovers Deluca and Termini [36] entropy:

  i.e., $V^{PFS}_{\sigma }(E) =-\frac{1}{n}\sum _{i=1}^{n}(\rho _E( \tilde{t_i})\log _2(\rho _E(\tilde{t_i}))+(1-\rho _E( \tilde{t_i}))\log _2(1-\rho _E( \tilde{t_i}))$

4.2 Justification

Before establishing the validity, we prove an inequality required for the validation of proposed measure.

Property 3.1

Under the condition P4 of Definition 3.1, we have

$$\left| \rho _E( \tilde{t_i})-\frac{1}{4}\right| +\left| \nu _E( \tilde{t_i})-\frac{1}{4}\right| +\left| \eta _E( \tilde{t_i})-\frac{1}{4}\right| +\left| \phi _E( \tilde{t_i})-\frac{1}{4}\right| \ge \left| \rho _F(\tilde{t_i})-\frac{1}{4}\right| +\left| \nu _F( \tilde{t_i})-\frac{1}{4}\right| +\left| \eta _F( \tilde{t_i})-\frac{1}{4}\right| +\left| \phi _F( \tilde{t_i})-\frac{1}{4}\right|$$

(17)

and

$$\left[ \rho _E( \tilde{t_i})-\frac{1}{4}\right] ^2+\left[ \nu _E( \tilde{t_i})-\frac{1}{4}\right] ^2+\left[ \eta _E(\tilde{t_i})-\frac{1}{4}\right] ^2+\left[ \phi _E( \tilde{t_i})-\frac{1}{4}\right] ^2 \ge \left[ \rho _F(\tilde{t_i})-\frac{1}{4}\right] ^2+\left[ \nu _F( \tilde{t_i})-\frac{1}{4}\right] ^2+\left[ \eta _F( \tilde{t_i})-\frac{1}{4}\right] ^2+\left[ \phi _F(\tilde{t_i})-\frac{1}{4}\right] ^2$$

(18)

Proof

If $\rho _E(\tilde{t_i}) \le \rho _F(\tilde{t_i}), \nu _E(\tilde{t_i}) \le \nu _F(\tilde{t_i})$ and $\eta _E(\tilde{t_i}) \le \eta _F( \tilde{t_i})$ with $\frac{1}{4} \ge$ max $\{\rho _F(\tilde{t_i}),\nu _F(\tilde{t_i}),\eta _F(\tilde{t_i})\}$ then $\rho _E(\tilde{t_i}) \le \rho _F(\tilde{t_i})\le \frac{1}{4},\nu _E( \tilde{t_i}) \le \nu _F(\tilde{t_i})\le \frac{1}{4}, \eta _E(\tilde{t_i}) \le \eta _F( \tilde{t_i})\le \frac{1}{4}$ and $\phi _E(\tilde{t_i}) \le \phi _F( \tilde{t_i})\ge \frac{1}{4}$, so it proves that (17) and (18) satisfied. Similarly, if $\rho _E(\tilde{t_i}) \ge \rho _F( \tilde{t_i}),\nu _E(\tilde{t_i}) \ge \nu _F( \tilde{t_i}), \eta _E( \tilde{t_i}) \ge \eta _F( \tilde{t_i})\le \frac{1}{4}$ with max $\{\rho _F(\tilde{t_i}),\nu _F(\tilde{t_i}),\eta _F(\tilde{t_i})\}\ge \frac{1}{4}$, then (17) and (18) hold. Since PFSs are the generalization of IFSs having four parameters ($\rho , \nu ,\eta ,\phi$), thus, extending the idea of intuitionistic fuzzy distance measure [60] to PFS, it is trivial from property (3.1), PFS F is closer to maximum value $\bigg (\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4}\bigg )$ than PFS E. $\square$

Theorem 3.1

Proposed measure defined in Equation (13) is an entropy measure for PFSs.

Proof

To establish (13), we shall prove the four axioms as discussed below:

P1: Let E is a crisp set that captures membership terms either $\rho _E(\tilde{t_i})=1,$ and $\nu _E( \tilde{t_i})=\eta _E(\tilde{t_i})=\phi _E(\tilde{t_i})=0$ or $\nu _E( \tilde{t_i})=1$ and $\rho _E( \tilde{t_i})=\eta _E( \tilde{t_i})=\phi _E( \tilde{t_i})=0$ or $\eta _E(\tilde{t_i})=1$ and $\rho _E(\tilde{t_i})=\nu _E( \tilde{t_i})=\phi _E( \tilde{t_i})=0$ or $\phi _E(\tilde{t_i})=1$ and $\rho _E(\tilde{t_i})=\nu _E( \tilde{t_i})=\eta _{E}( \tilde{t_i})=0.$

$\Rightarrow (\rho _E(\tilde{t_i})^{\sigma ^{-1}}+\nu _E( \tilde{t_i})^{\sigma ^{-1}}+\eta _E(\tilde{t_i})^{\sigma ^{-1}}+\phi _E( \tilde{t_i})^{\sigma ^{-1}})- (\rho _E( \tilde{t_i})^\sigma +\nu _E(\tilde{t_i})^\sigma +\eta _E( \tilde{t_i})^{\sigma }+\phi _E( \tilde{t_i})^\sigma )=0.$ Since $\sigma >0(\sigma \ne 1)$, $V^{PFS}_{\sigma }(E)=0$.

Conversely, if $V^{PFS}_{\sigma }(E)=0,$ we have

$$(\rho _E( \tilde{t_i})^{\sigma ^{-1}}+\nu _E( \tilde{t_i})^{\sigma ^{-1}}+\eta _E( \tilde{t_i})^{\sigma ^{-1}}+\phi _E(\tilde{t_i})^{\sigma ^{-1}})- (\rho _E( \tilde{t_i})^\sigma +\nu _E(\tilde{t_i})^\sigma +\eta _E(\tilde{t_i})^{\sigma }+\phi _E( \tilde{t_i})^\sigma )=0.$$

(19)

Since $\sigma >0(\sigma \ne 1)$, Equation (19) is possible in the following types:

• 1. either $\rho _E(\tilde{t_i})=1$ and $\nu _E(\tilde{t_i})=\eta _E(\tilde{t_i})=\phi _E( \tilde{t_i})=0$ or

• 2. $\nu _E(\tilde{t_i})=1$ and $\rho _E( \tilde{t_i})=\eta _E(\tilde{t_i})=\phi _E( \tilde{t_i})=0$ or

• 3. $\eta _E( \tilde{t_i})=1$ and $\rho _E(\tilde{t_i})=\nu _E(\tilde{t_i})=\phi _E( \tilde{t_i})=0$ or

• 4. $\phi _E(\tilde{t_i})=1$ and $\rho _E(\tilde{t_i})=\nu _E( \tilde{t_i})=\eta _{E}(\tilde{t_i})=0.$

As discussed above four types, we get $V^{PFS}_{\sigma }(E)=0$ if and only if E is a crisp set .

P2: From the construct of PFS, we have

$$\begin{aligned} \rho _E( \tilde{t_i})+\nu _E(\tilde{t_i})+\eta _E( \tilde{t_i})+\phi _E( \tilde{t_i})=1, \end{aligned}$$

therefore, we need to find the maximum value of $V^{PFS}_{\sigma }(E)$ (proposed entropy), we write $g(\rho _E,\nu _E,\phi _E)=\rho _E( \tilde{t_i})+\nu _E( \tilde{t_i})+\eta _E+\phi _E(\tilde{t_i})-1$ and by considering $\lambda$ known as Lagrange’s multipliers , we design the following Lagrange’s function as:

$$G(\rho _E,\nu _E,\phi _E)=V^{PFS}_{\sigma }(\rho _E,\nu _E,\eta _E,\phi _E)+\lambda g(\rho _E,\nu _E,\eta _E,\phi _E).$$

(20)

To complete the proof of maximality, differentiate Equation (20) partially with respect to $\rho _M,\nu _M,\eta _M,\phi _M$ and $\lambda$ and equate each equal to zero, we get $\rho _E(\tilde{t_i})=\nu _E(\tilde{t_i})=\eta _E(\tilde{t_i})=\phi _E( \tilde{t_i})=\frac{1}{4}$. It is trivial and easy that all the partial order differentiation becomes zero and we get $\rho _E( \tilde{t_i})=\nu _E(\tilde{t_i})=\phi _E( \tilde{t_i})=\eta _E(\tilde{t_i})=\frac{1}{4}$. The stationary point of $V^{PFS}_{\sigma }(E)$ is $\rho _E( \tilde{t_i})=\nu _E(\tilde{t_i})=\eta _E( \tilde{t_i})=\phi _E( \tilde{t_i})=\frac{1}{4}.$

Next, we prove $V^{PFS}_{\sigma }(E)$ is a concave function with the help of Hessian matrix.

Definition 3.2

The Hessian matrix (HeM) of a function $\oplus (x_1,x_2,x_3,x_4)$ of four variables is depicted as:

$$HeM( \oplus ) = \left[ {\begin{array}{*{20}c} {\frac{{\delta ^{2} \oplus }}{{\delta x_{1}^{2} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{2} \delta x_{1} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{3} \delta x_{1} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{4} \delta x_{1} }}} \\ {\frac{{\delta ^{2} \oplus }}{{\delta x_{1} \delta x_{2} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{2}^{2} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{3} \delta x_{2} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{4} \delta x_{2} }}} \\ {\frac{{\delta ^{2} \oplus }}{{\delta x_{1} \delta x_{3} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{2} \delta x_{3} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{3}^{2} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{4} \delta x_{3} }}} \\ {\frac{{\delta ^{2} \oplus }}{{\delta x_{1} \delta x_{4} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{2} \delta x_{4} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{3} \delta x_{4} }}} & {\frac{{\delta ^{2} \oplus }}{{\delta x_{4}^{2} }}} \\ \end{array} } \right]$$

The function $\oplus$ is said to be strictly convex if $HEN (\oplus )$ is positive definite (PD) and concave if $HeM (\oplus )$ is negative definite (ND) and The Hessian of $V^{PFS}_{\sigma }(E)$ is given by

$$HeM(V_{\sigma }^{{PFS}} (E)) = \frac{p}{{n(\sigma - \sigma ^{{ - 1}} )}}\left[ {\begin{array}{*{20}l} { - 1} \hfill & {0} \hfill & {0} \hfill & {0} \hfill \\ 0 \hfill & { - 1} \hfill & {0} \hfill & {0} \hfill \\ 0 \hfill & {0} \hfill & { - 1} \hfill & {0} \hfill \\ 0 \hfill & {0} \hfill & {0} \hfill & { - 1} \hfill \\ \end{array} } \right]$$

which is ND for all $\sigma >0(\ne 1)$, where $p= \sigma (\sigma -1)4^{(2-\sigma )}-\sigma ^{-1}(\sigma ^{-1}-1)4^{(2-\sigma ^{-1})}.$ Therefore, $V^{PFS}_{\sigma }(E)$ is strictly a concave measure for all $\sigma >0(\ne 1)$ with $\rho _E( \tilde{t_i})=\nu _E(\tilde{t_i})=\eta _E( \tilde{t_i})=\phi _E( \tilde{t_i})=\frac{1}{4}$ as maximal point.

P3: Since, $V^{PFS}_{\sigma }(E)$ is a concave function of $E\in PFS(\Game ),$ with maximum value at stationary point, then if max$\{\rho _E(\tilde{t_i}),\nu _E( \tilde{t_i}),\eta _E(\tilde{t_i}),\phi _E(\tilde{t_i})\}\le \frac{1}{4}$, then $\rho _E( \tilde{t_i})\le \rho _F(\tilde{t_i}), \nu _E( \tilde{t_i})\le \nu _F(\tilde{t_i})$ and $\eta _E( \tilde{t_i})\le \eta _F( \tilde{t_i})$ implies $\phi _E( \tilde{t_i})\ge \phi _F( \tilde{t_i})\ge \frac{1}{4}.$ Therefore, by using property (3.1), we see that $V^{PFS}_{\sigma }(E)$ holds the condition P4.

Similarly, if min$\{\rho _E(\tilde{t_i}),\nu _E(\tilde{t_i}),\eta _E( \tilde{t_i})\}\ge \frac{1}{4}$, then $\rho _E( \tilde{t_i})\le \rho _F(\tilde{t_i}),\nu _E( \tilde{t_i})\ge \nu _F(\tilde{t_i})$ and $\eta _E(\tilde{t_i})\ge \eta _F(\tilde{t_i})$. Again, by using property (3.1), function $V^{PFS}_{\sigma }(E)$ satisfies axiom P4.

P4: For any PFS, $V^{PFS}_{\sigma }(E)=V^{PFS}_{\sigma }(E^c)$, which is straightforward.

Theorem 3.2

For two PFSs E and F such that for all $\tilde{t_i}\in \Game$, either $E\subseteq F$ or $F\subseteq E;$ then,

$$\begin{aligned} V^{PFS}_{\sigma }(E\cup F)+V^{PFS}_{\sigma }(E\cap F)=V^{PFS}_{\sigma }(E)+V^{PFS}_{\sigma }(F). \end{aligned}$$

Proof

Separate set $\Game$ into two parts say $\Game _1$ and $\Game _2$, such that

$$\begin{aligned}&\Game _1=\{ \tilde{t_i} \in \Game :E\subseteq F\} \quad \mathrm {and}\quad \Game _2=\{ \tilde{t_i} \in \Game :E\supseteq F\} \nonumber \\&\rho _E( \tilde{t_i}) \le \rho _F( \tilde{t_i}),\nu _E( \tilde{t_i}) \le \nu _F( \tilde{t_i}),\eta _E( \tilde{t_i})\ge \eta _F( \tilde{t_i}) \qquad \forall \qquad \tilde{t_i} \in \Game _1 \nonumber \\&\rho _E( \tilde{t_i}) \ge \rho _F( \tilde{t_i}),\nu _E(\tilde{t_i}) \ge \nu _F( \tilde{t_i}),\eta _E( \tilde{t_i}) \ge \eta _F( \tilde{t_i}) \qquad \forall \qquad \tilde{t_i} \in \Game _2 \nonumber \\&\mathrm {Now},\; V^{PFS}_{\sigma }(E\cup F)= {} \frac{1}{n(\sigma -\sigma ^{-1})}\nonumber \\&\sum _{i=1}^{n}\bigg [( \rho _{(E\cup F)}( \tilde{t_i})^{\sigma ^{-1}}+\nu _{(E\cup F)}(\tilde{t_i})^{\sigma ^{-1}}+\eta _{(E\cup F)}( \tilde{t_i})^{\sigma ^{-1}}\nonumber \\&+\phi _{(E\cup F)}( \tilde{t_i})^{\sigma ^{-1}}) -\left( \rho _{(E\cup F)}(\tilde{t_i})^{\sigma }+\nu _{(E\cup F)}( \tilde{t_i})^{\sigma }\right. \nonumber \\&\left. +\eta _{(E\cup F)}(\tilde{t_i})^{\sigma }+\phi _{(E\cup F)}( \tilde{t_i})^{\sigma } \right) \bigg ] \nonumber \\&=\frac{1}{n(\sigma -\sigma ^{-1})}\nonumber \\&\sum _{\Game _1}\left[ \left( \rho _F( \tilde{t_i})^{\sigma ^{-1}}+\nu _F( \tilde{t_i})^{\sigma ^{-1}}+\phi _F( \tilde{t_i})^{\sigma ^{-1}}\right. \right. \nonumber \\&\left. \left. -\left( \rho _F( \tilde{t_i})^{\sigma }+\nu _F( \tilde{t_i})^{\sigma }+\phi _F(\tilde{t_i})^{\sigma } \right) \right) \right] \nonumber \\&+\frac{1}{n(\sigma -\sigma ^{-1})}\nonumber \\&\sum _{\Game _2}\left[ \left( \rho _E( \tilde{t_i})^{\sigma ^{-1}}+\nu _E( \tilde{t_i})^{\sigma ^{-1}}+\phi _E( \tilde{t_i})^{\sigma ^{-1}} \right) \right. \nonumber \\&\left. -\left( \rho _E(\tilde{t_i})^{\sigma }+\nu _E( \tilde{t_i})^{\sigma }+\phi _E(\tilde{t_i})^{\sigma } \right) \right] \end{aligned}$$

(21)

Similarly, we get

$$\begin{aligned}&V^{PFS}_{\sigma }(E\cap F) =\frac{1}{n(\sigma -\sigma ^{-1})}\nonumber \\&\quad \sum _{\Game _1}\left[ \left( \rho _E( \tilde{t_i})^{\sigma ^{-1}}+\nu _E( \tilde{t_i})^{\sigma ^{-1}}+\phi _E( \tilde{t_i})^{\sigma ^{-1}}\right. \right. \nonumber \\&\quad \quad \left. \left. -\left( \rho _E(\tilde{t_i})^{\sigma }+\nu _E( \tilde{t_i})^{\sigma }+\phi _E( \tilde{t_i})^{\sigma } \right) \right) \right] \nonumber \\&\quad +\frac{1}{n(\sigma -\sigma ^{-1})}\sum _{\Game _2}\left[ \left( \rho _F( \tilde{t_i})^{\sigma ^{-1}}+\nu _F( \tilde{t_i})^{\sigma ^{-1}}+\phi _F( \tilde{t_i})^{\sigma ^{-1}} \right) \right. \nonumber \\&\left. -\left( \rho _F(\tilde{t_i})^{\sigma }+\nu _F( \tilde{t_i})^{\sigma }+\phi _F(\tilde{t_i})^{\sigma } \right) \right] \end{aligned}$$

(22)

Now, adding (21) and (22), we have

$$\begin{aligned} V^{PFS}_{\sigma }(E\cup F)+V^{PFS}_{\sigma }(E\cap F)=V^{PFS}_{\sigma }(E)+V^{PFS}_{\sigma }(F) \end{aligned}$$

5 Illustrative Examples

In this section, to verify the feasibility of new proposed entropy, we will compare it with other entropy measures through numerical examples.

Example 4.1

Let $\Game =\{{\tilde{t}}\}$. Define two PFSs on $\Game$ as $E=\{\left\langle {\tilde{t}}, \{0.48,0.31,0.27\} \right\rangle \}$ and $F=\{\left\langle {\tilde{t}}, \{0.32,0.54,0.12\} \right\rangle \}.$

We can calculate the entropies of E and F, as depicted in Table 1 .

Table 1 Comparison between entropies of two PFSs

The data in Table 1 show that the entropy proposed by Wei [7] cannot discriminate the entropy of two different sets. However, Arya and Kumar [34] entropy and the proposed entropy measure for different values of parameter $\sigma$ can clearly distinguishing the entropy of PFSs of E and F.

Example 4.2

Let the universe of discourse be $\Game =\{\tilde{t_1},\tilde{t_2}\}$ and let

$$\begin{aligned} E=\{\left\langle \tilde{t_1}, \{0.581,0.324,0.129\} \right\rangle , \left\langle \tilde{t_2}, \{0.584,0.317,0.132\} \right\rangle \}; \\ F=\{\left\langle \tilde{t_1}, \{0.578,0.326,0.130\} \right\rangle , \left\langle \tilde{t_2}, \{0.581,0.319,0.135\} \right\rangle \} \end{aligned}$$

be two PFSs on $\Game$. We notice that E and F are different. Therefore, we want the entropy of E to be different from that of F. By calculating, we get Arya and Kumar [34] entropy that gives 0.9874 for sets E and F, that is, the entropies of E and F are equal. However, the entropies $V^{PFS}_{\sigma }$ for E and F are different ($V^{PFS}_{\sigma }(E)=1.427$, $V^{PFS}_{\sigma }(F)=1.423$). The reason for the small difference in entropy between E and F is that E and F sets are very close to each other. Hence, the proposed parametric measure is more effective.

6 Uncertain Multicriterion Decision-Making Approach Based on TODIM-ELECTRE Method

This section presents a MCDM method based on the TODIM-ELECTRE method for local partner evaluation under picture fuzzy setting with the help of an illustrated example. Specifically, we extend TODIM method with ELECTRE method to decision-making for the case multi criterion , based on the entropy weights. For the MCDM problem with PF uncertainty, let $\oslash=\{\oslash _1,\oslash _2,\ldots ,\oslash _m\}$ be m-rows of the alternatives or candidates and $c=\{c_1,c_2,\ldots ,c_n\}$ be n-columns of criterions.

Consider the assessment information of alternative $\oslash _i$ on the basis of the criterion $c_j$ is denoted in terms of PF value $\gamma _{ij}=(\rho _{ij},\nu _{ij},\eta _{ij});1\le i \le m,1\le j \le n.$ To determine the degrees of positive membership ($\rho _{ij}$), neutral membership ($\nu _{ij}$ ), and negative membership ($\eta _{ij}$ ), we suggest the following statistical tool:

$$\begin{aligned} \rho _{ij}=\frac{n_{Pos}(i,j)}{N}, \nu _{ij}=\frac{n_{Neu}(i,j)}{N}, \rho _{ij}=\frac{n_{Neg}(i,j)}{N} \end{aligned}$$

(23)

where N denotes the total number of DMs, $n_{Pos}(i,j)$ represents the number of DMs supporting the $i^th$ alternative corresponding to $j^th$ criteria, $n_{Neu}(i,j)$ denotes the number of DMs who remain abstain during the decision process, and $n_{Neg}(i,j)$ represents the number of decision-makers not favoring the $i^th$ alternative corresponding to $j^th$ criteria. For example, suppose that ten DMs are invited to evaluate an alternative $\oslash _i$ under a certain criterion $c_j$. Three DMs give ”high” grades, four DMs give ”medium” grades, two DMs provide ”low” grades, and the last one refuses to provide an answer. Then, the situation can be described by a PF number $\gamma _{ij}=(0.3, 0.4, 0.2)$. Thus, using (23), a MCDM problem can be represented by the decision matrix ${\varvec{D}}=[\gamma _{ij}]_{m\times n}$ as follows:

$$D= [\gamma _{{ij}} ]_{{m \times n}} = \begin{array}{*{20}c} {} \\ { \oslash } \\ { \oslash } \\ \vdots \\ {\oslash_{m} } \\ \end{array} \left[ {\begin{array}{*{20}c} {c_{1} } & {c_{2} } & { \cdots } & {c_{n} } \\ {(\rho _{{11}} ,\nu _{{11}} ,\eta _{{11}} )} & {(\rho _{{12}} ,\nu _{{12}} ,\eta _{{12}} )} & { \cdots } & {(\rho _{{1n}} ,\nu _{{1n}} ,\eta _{{1n}} )} \\ {(\rho _{{21}} ,\nu _{{21}} ,\eta _{{21}} )} & {(\rho _{{22}} ,\nu _{{22}} ,\eta _{{22}} )} & { \cdots } & {(\rho _{{2n}} ,\nu _{{2n}} ,\eta _{{2n}} )} \\ \vdots & { \vdots } & { \ddots } & { \vdots } \\ {(\rho _{{m1}} ,\nu _{{m1}} ,\eta _{{m1}} )} & {(\rho _{{m2}} ,\nu _{{m2}} ,\eta _{{m2}} )} & { \cdots } & {(\rho _{{mn}} ,\nu _{{mn}} ,\eta _{{mn}} )} \\ \end{array} } \right]$$

(24)

Usually, the criterion vector weights vector information is partially known or completely unknown due to the limited time and insufficient knowledge of experts in the real-life decision-making problems. Hence, the determination of criterion’s weights vector is an active issue in MCDM problems in which the criterion weights are completely / partially known or unknown. Here, we will put forward an entropy-based approach to determine the weights vector, which then effectively lead the reasonable results.

The steps of the proposed decision model based on entropy, PF-TODIM, and ELECTRE methods are described as below:

Step 1: Normalize the picture fuzzy decision matrix (PFM) ${\varvec{D}}=(\gamma _{ij})_{m\times n}$, denoted by $\varvec{D^N}=[q_{ij}]_{m\times n}$ as follows:

$$\begin{aligned} q_{{ij}} = \left\{ {\begin{array}{*{20}c} {(\gamma _{{ij}} )^{c} ,} & { {\text{for cost criteria}}} \\ {\gamma _{{ij}} ,} & { {\text{for efficient criteria }}} \\ \end{array} } \right.\end{aligned}$$

(25)

where $\gamma _{ij}^c=(\eta _{ij}, \nu _{ij},\rho _{ij})$. Then, we obtained a normalized PFM $D=(q_{ij})_{m\times n}$ Step 2:

6.1 Partially Known Criterion Weights Information

If the criterion weight information is not partially/entirely known, first, the entropy information should be calculated by us. The overall entropy of alternative $\oslash _i$ over the criterion $c_j$ is given below:

$$\begin{aligned} V^{PFS}_{\sigma }(\oslash _i)=\sum _{j=1}^{n}V^{PFS}\left( \rho _{ij}, \nu _{ij},\eta _{ij},\phi _{ij} \right) , \end{aligned}$$

(26)

where

$$V_{\sigma }^{{PFS}} \left( {\rho _{{ij}} ,\nu _{{ij}} ,\eta _{{ij}} ,\phi _{{ij}} } \right) = \frac{1}{{n(\sigma - \sigma ^{{ - 1}} )}}\sum_{i = 1}^n [(\rho _{{ij}}^{{\sigma ^{{ - 1}} }} + \nu _{{ij}}^{{\sigma ^{{ - 1}} }} + \eta _{{ij}}^{{\sigma ^{{ - 1}} }} + \phi _{{ij}}^{{\sigma ^{{ - 1}} }} ) - (\rho _{{ij}}^{\sigma } + \nu _{{ij}}^{\sigma } + \eta _{{ij}}^{\sigma } + \phi _{{ij}}^{\sigma } )].$$

(27)

The parameter $\sigma$ reflects the uncertainty or fuzzy information. It provides more malleability to the proposed measure for practical purposes. The one parametric models are more flexible and reliable to use in certain situations. For example, in the recent scenario of pandemic COVID-19, the uncertainty had been very high. Most of the businesses were at their low but with the advent of various vaccines, the situation is getting improved. Clearly, this is a case of uncertainty with different levels at different points in time. In our model, $\sigma$ is the measure of this uncertainty due to pandemic situation. We can set the following model of minimizing objective optimization proposed by Wang and Wang [43] to measure the information about weights:

$$\begin{aligned}&\text {min}(T)=\sum _{i=1}^{m}\left( w_j.V^{PFS}_{\sigma }(\oslash _i) \right) \nonumber \\&\quad =\sum _{i=1}^{m}\left[ w_j\bigg (V^{PFS}\left( \rho _{ij}, \nu _{ij},\eta _{ij},\phi _{ij} \right) \bigg ) \right] \nonumber \\&\quad =\frac{1}{n(\sigma -\sigma ^{-1})}\sum _{i=1}^{m}\sum _{j=1}^{n}\bigg [w_j\bigg (( \rho _{ij} ^{\sigma ^{-1}}+\nu _{ij}^{\sigma ^{-1}}+\eta _{ij} ^{\sigma ^{-1}}+\phi _{ij}^{\sigma ^{-1}} ) \nonumber \\&\quad -(\rho _{ij}^{\sigma }+\nu _{ij}^{\sigma }+\eta _{ij}^{\sigma }+\phi _{ij}^{\sigma } )\bigg ) \bigg ], \end{aligned}$$

(28)

where $w_j \in H$ satisfying $\sum _{j=1}^{n}w_j=1$. On solving the above Equation (28), we obtain the weight index by arg min T=$\left( w_1,w_2,\ldots ,w_n \right) '$ where $'$ stands for transpose.

Apart from this, there are certain other programming algorithms proposed by researchers in the literature. Optimization is the process of defining the decision variables of a function to minimize or maximize its values [61]. Dhiman and Kaur [62] proposed bio-inspired algorithm called Sooty Tern Optimization Algorithm (STOA) for solving constrained industrial problems. Various machine learning algorithms have been utilized to perform analysis for screening COVID-19 [63]. Dhiman and Kumar [64] proposed a novel bio-inspired competitive algorithm as compared with other optimization algorithms. However, these algorithms are quite useful in practical applications and will be reported somewhere else in future under picture fuzzy environment.

Step 3:

6.2 TODIM Method

Up to date, TODIM method [46, 47] has been used by previous authors. TODIM represents the dominance of each option/alternative ($\oslash _i$) over the others to design a function of multicriteria values.

Determine $w_{jr}=\frac{w_j}{w_r}\left( 1 \le j,r \le n\right)$, where $w_r=\text {max}\{w_j\}$. With Equation (28), find out the dominance degree of the alternative $\oslash _i$ over each alternative $\oslash_j$ with respect to each criterion $c_j$. The formula is depicted as:

$$\begin{aligned}dom_{j} ( { \oslash }_{i} ,\oslash_{k} ) = \left\{ {\begin{array}{*{20}c} {\sqrt {\frac{{w_{{jr}} d_{H} (q_{{ij}} ,q_{{kj}} )}}{{\sum\limits_{{j = 1}}^{n} {w_{{jr}} } }},} } & {{\text{if }}\qquad q_{{ij}} > q_{{kj}} } \\ {0,} & {{\text{if}}\qquad q_{{ij}} = q_{{kj}} } \\ { - \frac{1}{\gamma }\sqrt {\frac{{\left( {\sum\limits_{{j = 1}}^{n} {w_{{jr}} } } \right)d_{H} (q_{{ij}} ,q_{{kj}} )}}{{w_{{jr}} }}} } & {{\text{if}}\qquad q_{{ij}} < q_{{kj}} } \\ \end{array} } \right.\end{aligned}$$

(29)

where $d_H(q_{ij},q_{kj})$ is to measure the distance between $q_{ij}$ and $q_{kj}$ under $\oslash_j$ . In the above expression, there is a constant parameter $\gamma$, which is used to represent the sensitive coefficient of risk aversion and known as reduction factor of losses. When the parameter $\gamma$ has different values, the values of subfunction $dom_j(\oslash _i,\oslash_{k})$ will change correspondingly. Table 2 summarizes the frequently used notations and descriptions.

Step 4: Work out the dominance matrix of each alternative $\oslash _i$ over each criterion $c_j$ by

$$\begin{gathered} \hfill \\ Z_{j} = [dom_{j} ({ \oslash },\oslash_{k} )]_{{m \times m}} = \begin{array}{*{20}c}{} \\ { \oslash } \\ { \oslash } \\ \vdots \\ {\oslash_{m} } \\ \end{array} \left[ {\begin{array}{*{20}c}{c_{1} } & {c_{2} } & \cdots & {c_{m} } \\ 0 & {Z_{j} ({ \oslash }_{1} ,{ \oslash }_{2} )} & \cdots & {Z_{j} ({ \oslash }_{1} ,\oslash_{m} )} \\ {Z_{j} ({ \oslash }_{2} ,{ \oslash }_{1} )} & 0 & \cdots & {Z_{j} ({ \oslash }_{2} ,\oslash_{m} )} \\ \vdots & \vdots & \ddots & \vdots \\ {Z_{j} (\oslash_{m} ,{ \oslash }_{1} )} & {Z_{j} (\oslash_{m} ,{ \oslash }_{2} )} & \cdots & 0 \\ \end{array} } \right] \hfill \\ \end{gathered}$$

(30)

Table 2 Nomenclature

6.3 ELECTRE

The ELECTRE approach is taken to adopt the ranking results of alternatives. The essential steps are as given below.

Step 5: Determine the concordance index $H(\oslash _i,\oslash _k)$ of alternatives $\oslash _i$ and $\oslash _k(i,k=1,2,\ldots ,m)$ is formulated as

$$\begin{aligned} G_j(\oslash _i,\oslash _k)= & {} {\left\{ \begin{array}{*{20}c}0, dom_j(\oslash _i,\oslash _k)\ge g_j\\ 1, dom_j(\oslash _i,\oslash _k)\le h_j\\ {\frac{g_j-dom_j(\oslash _i,\oslash _k)}{g_j-h_j}}, h_j < dom_j(\oslash _i,\oslash _k)\le g_j, \end{array}\right. } \end{aligned}$$

(31)

$$\begin{aligned} H(\oslash _i,\oslash _k)= & {} \sum _{j=1}^{n}\left( w_j.G_j(\oslash _i,\oslash _k)\right) , \end{aligned}$$

(32)

where $G_j(\oslash _i,\oslash _k)$ represents the concordance degree of alternatives $\oslash _i$ and $\oslash _k (i,k=1,2,\ldots ,m)$ under criterion $c_j(j=1,2,\ldots ,n)$, $h_j$ and $g_j$ are reported the preference and indifference thresholds, respectively, under criterion $c_j(j=1,2,\ldots ,n)$ and $g_j\ge h_j \ge 0.$

Step 6: The discordance index $P_j(\oslash _i,\oslash _k)$ of alternatives $\oslash _i$ and $\oslash _k (i,k=1,2,\ldots ,m)$ under criterion $c_j(j=1,2,\ldots ,n)$ is calculated by

$$\begin{aligned} P_j(\oslash _i,\oslash _k)= {\left\{ \begin{array}{ll}0, dom_j(\oslash _i,\oslash _k)\ge g_j\\ 1, dom_j(\oslash _i,\oslash _k)\le l_j\\ {\frac{dom_j(\oslash _i,\oslash _k)-g_j}{l_j-g_j}}, g_j < dom_j(\oslash _i,\oslash _k)\ge l_j, \end{array}\right. } \end{aligned}$$

(33)

where $l_j$ stands for veto thresholds under criterion $c_j(j=1,2,\ldots ,n)$ and $l_j\ge g_j \ge 0.$

Step 7: Based on $H(\oslash _i,\oslash _k)$ and $P_j(\oslash _i,\oslash _k)$, the credibility index $Q(\oslash _i,\oslash _k)$ of alternative $\oslash _i$ over $\oslash _k (i,k=1,2,\ldots ,m)$ is computed by

$$\begin{aligned}&R_j(\oslash _i,\oslash _k)= {\left\{ \begin{array}{ll}\frac{1-P_j(\oslash _i,\oslash _k)}{1-H(\oslash _i,\oslash _k)}, \mathrm {if}\; P_j(\oslash _i,\oslash _k) > H(\oslash _i,\oslash _k)\\ 1, \mathrm {if}\; P_j(\oslash _i,\oslash _k) \le H(\oslash _i,\oslash _k) \end{array}\right. } \end{aligned}$$

(34)

$$\begin{aligned}&Q(\oslash _i,\oslash _k)=H(\oslash _i,\oslash _k).\prod _{j=1}^n R_j(\oslash _i,\oslash _k), \end{aligned}$$

(35)

where $R_j(\oslash _i,\oslash _k)$ is the credibility degree of alternatives $\oslash _i$ and $\oslash _k$ $(i,k=1,2,\ldots ,m)$ under criterion $c_j(j=1,2,\ldots ,n)$.

Step 8: The ranking index $S(\oslash _i)$ of alternatives $\oslash _i(i=1,2,\ldots ,n)$ is computed by

$$\begin{aligned} S(\oslash _i)=\sum _{k=1}^{m}Q(\oslash _i,\oslash _k)-\sum _{k=1}^{m}Q(\oslash _k,\oslash _i). \end{aligned}$$

(36)

Corresponding to the value of $S(\oslash _i)$, the final or optimal ranking order of alternatives is obtained. Or we can say, the bigger the value of $S(\oslash _i)$ is, the higher the ranking of alternative $\oslash _i.$

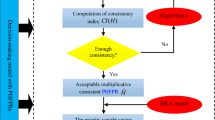
Figure 1 shows the general framework of the proposed study.

Fig. 1

General Framework of the proposed study

7 Solution of Decision-Making Problem

Suppose that in INDIA, a multinational footwear company desires to hire a local investment partner to expand its business in this country. There are five alternative candidate partners that have been considered after preliminary screening. To determine the five alternatives, five criteria are used, which are management level ($c_1$), local reputation ($c_2$), level of priority relationship ($c_3$), education and resources ($c_4$), and innovation capability ($c_5$), respectively. In order to ensure the validity and accuracy of the evaluation information, there is no indication about any decision made during the evaluation process and the experts are not allowed to communicate with each other. Using PF information given by the ten DMs under the five criteria, the five possible alternative $\oslash _i(i=1,2,\ldots ,5)$ will be evaluated as depicted in the following Table 3:

Table 3 PF values given by DMs

Step 1: Since all the criterion’s are benefit type, therefore no need to be normalized. Thereafter, we take the developed method to obtain the optimal alternative(s).

Step 2: The criterions weights vector information is partially known as:

$$T=\{ 0.12\le w_1\le 0.26,0.17\le w_2\le 0.19, 0.28\le w_3\le 0.39,0.19\le w_4\le 0.46, 0.10\le w_5\le 0.16, w_j\ge 0, \sum _{j=1}^{5}w_j=1\}.$$

With Equation (27), the overall entropy values of the criterion are determined as follows: $K_1=1.5494$, $K_2=1.2062$, $K_3=1.5619$, $K_4=1.5950$, and $K_5=1.6894$ (Tables 4, 5, 6, 7, 8, 9).

The following model of linear programming is used to determine the weights vector:

$$\begin{aligned}&Min \;T=1.5494w_1+1.2062w_2+1.5619w_3+1.5950w_4\\&\quad +1.6984w_5 \;\mathrm {subjected\; to\; w\in T}. \end{aligned}$$

From this model, we get the weight vector of criteria:

$$\begin{aligned} w=(0.12,0.17,0.19,0.36,0.16)^T. \end{aligned}$$

Step 3 and 4: Let $\gamma =2.5$. Then, the dominance index matrices of the alternative $\oslash _i$ over the criteria $c_j (\; 1\le j\le 5)$ are as given below:

Table 4 Dominance matrix 1

Table 5 Dominance matrix II

Table 6 Dominance matrix III

Table 7 Dominance matrix IV

Table 8 Dominance matrix V

Step 5: Using Equation (32), the concordance index can be obtained as:

Table 9 Concordance index $H(\oslash _i,\oslash _k)$

Step 6: Using Equation (33), the discordance degree under each criterion is depicted in Tables 10, 11, 12, 13, and 14.

Table 10 Discordance degree for criterion index $c_1$

Table 11 Discordance degree for criterion index $c_2$

Table 12 Discordance degree for criterion index $c_3$

Table 13 Discordance degree for criterion index $c_4$

Table 14 Discordance degree for criterion index $c_5$

Table 15 Credibility index

Step 7: The credibility index can be obtained from Equation (35) and numerical values are depicted in Table 15.

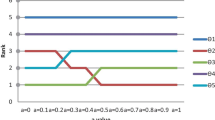
Step 8: At last, the ranking results of all are determined by using Equation (36) as follows: $S(\oslash _1)=0.012$, $S(\oslash _2)=0.446$, $S(\oslash _3)=-0.987$, $S(\oslash _4)=1.038$, and $S(\oslash _5)=-0.509.$ The ranking result of alternatives is $\oslash _4 \succ \oslash _2 \succ \oslash _1 \succ \oslash _5 \succ \oslash _3$ and the best partner is $\oslash _4$ .

8 Comparison Discussion

In this section, we discuss the comparison study on how our proposed entropy-based MCDM model is reliable, feasible, and effective to aggregate the fuzzy information for PFSs. This comparison study is carried out to compare the innovative characteristics of the various decision-making methods present in literature. We use existing literatures like Wang et al. [65], Tian et al. [66], Nei [25], and the proposed model to deal with the above same example and the index values and results are shown in Tables 16 and 17, respectively. With a comparison of the existing approaches, the proposed model considers the criterion’s weights and therefore, this study can effectively lead the reasonable ranking orders.

Table 16 Ranking index values of the alternatives by using existing standards

Table 17 Comparison results by different existing methods

• 1. Wang et al. [65] used Bonferroni mean distance to determine the weights vector methods, that is, do not use entropy measure to integrate information, which can effectively eliminate the distortion of evaluation information. Hence, proposed model provides better results than Wang et al. [65].

• 2. Tian et al's. [66] method is not able to get sensible results as they used aggregation operators. Also, aggregation operators include different functions, so DMs can select much better aggregation operators according to the practically decision-making environment. The main reason is that, aggregation operators ignore actual weight information and consider the experts weight, which can bring data misfortune and bending.

• 3. When we compared with Nei [25], both the models are successfully deal with linguistic variables, but they have obtained different ranking results. In the proposed model, first we obtained dominance matrix, then ranking have been obtained from ELECTRE method. Therefore, the proposed model is more effective to tackle with the uncertain MCDM problems.

To further demonstrate the effectiveness of our method, the problems in Wang et al. [32] and Wei et al. [33] are also solved by other existing methods. These ranking results are listed in Table 18. In Wang et al. [32] and Wei et al. [33], the weights of criteria were known in advance, which is uncommon in real decision-making process. In Tolga et al. [67] , the criteria weights vector was evaluated with crisp numbers directly given by DMs, which contains strong subjectivity. However, objective criteria weights determination models have been constructed in Wang et al. [32] and this study. Furthermore, the VIKOR method has poor robustness, because the ranking results are susceptible to the relative importance of individual regret values and group utility values [68]. In contrast, the traditional TODIM [67] is integrated with ELECTRE in this study and its great robustness was proved through comparative analyses. It is clear that our ranking is always closest to the best ranking order.

Table 18 Ranking results with different methods

Obviously, from the above-mentioned discussion, we can be concluded that our entropy-based weighting approach and integrated method can effectively refine the unreasonable information for the alternatives. The proposed method has the capability to reduce the loss of information and more accuracy because of the combination of the entropy, TODIM, and ELECTRE.

Due to the complexity of human subjectivity and objective things, MCDM problems are often inconsistent, uncertain, so the decision information often given is unclear. Therefore, this technique is more applicable when the information in MCDM problems in real life is unclear or there is a large amount of data. Some main merits of the proposed decision model are given as below:

• Firstly, the present study takes the advantages of PFSs and entropy concurrently to deal with the uncertain and imprecise information.

• Secondly, we proposed PF TODIM-ELECTRE and to introduce a new ranking method with uncertain conditions, which then leads to stable decisions and enriches the theory of MCDM.

The proposed model may be applied to a variety of disciplines such as pattern recognition, clustering problems, medical diagnosis, fault diagnosis, and selection processes such as the selection of suppliers, facility locations, site selection, project installation, optimal renewable energy sources, and so on.

9 Conclusions

The assessment and selection of the sustainable partner are significant issues in supplier problem. Due to increased environmental issues, involvement of several influencing factors, and uncertainty of human mind , the sustainable partner selection procedure can be treated as an uncertain MCDM problem. Since PFSs are more significant to describe the uncertain information, therefore, this study has developed a new picture fuzzy entropy measure by exploring the concept of Havrda–Charvat–Tsalli’s entropy from probabilistic settings to picture fuzzy settings and validate its properties. Further, a new MCDM model has been developed for assessing sustainable partners' options under PFSs environment. This model has been introduced with the integration of classical TODIM approach, ELECTRE approach, and PF information measures within the perspective of PFSs. To evaluate the objective criteria weights, novel entropy measure has been proposed under PFS context. Further, the integrated TODIM-ELECTRE methodology has been applied to evaluate the best partner on PFSs settings, which display the feasibility and practicality of PF TODIM-ELECTRE approach. To validate the results, a comparison with existing method has been conferred. The outcomes obtained by the PF TODIM-ELECTRE model prove that the introduced model has a well-mannered steadiness and effectiveness and is well consistent with the extant models. As a conclusion, it is shown that entropy-based PF TODIM-ELECTRE is quite robust since entropy measure does not generally create an undesired ranking solution.

On the other hand, there are some limitations that must be improved in future research, given as:

• The approach proposed herein cannot deal with the correlative MCDM problems.

• This paper has limitation to handle the indeterminate and inconsistent information in a more precise environment.

• The importance degrees of experts are assumed the same. Thus, the proposed approach can be improved by overcoming these drawbacks.

In future, the new MCDM method will be suggested in some more risk analysis problems such as in the emerging technology, project ranking, image processing, industrial engineering, and so forth.