Introduction and review of the literature

A tool which represents the partnership or relationship function is called a Fuzzy Set (FS) and handles the real-world problems in which generally some type of uncertainty exists [1]. This concept was generalized by Atanassov [2] to intuitionistic fuzzy set (IFS) which is determined in terms of membership (MS) and non-membership (NMS) functions, the characteristic functions of the set. Beside this, several theories have been developed for uncertainties, including generalized orthopair FSs [3], Pythagorean FSs [4], picture FSs [5], hesitant interval-based neutrosophic linguistic sets [6], N-valued interval neutrosophic sets (NVINSs) [7], generalized interval-valued triangular intuitionistic FSs [8], interval-valued trapezoidal intuitionistic FSs [9], interval-valued Pythagorean FSs [10], interval-valued IFSs [11], and interval type 2 FSs [12].

In 1995, Smarandache [13] premises the theme of neutrosophic sets (NS). The NS is to be a set of elements having a membership degree, indeterminate membership and also non-membership with the criterion less than or equal to 3. The neutrosophic number is an exceptional type of neutrosophic sets that extend the domain of numbers from those of real numbers to neutrosophic numbers. By generalizing SVNSs [14], Wang et al. premised the idea of IVNS. The IVNS [15] is a more general database to generalize the concept of different types of sets to express membership degrees’ truth, indeterminacy, and a false degree in terms of intervals. Thus, several papers are published in the field of fuzzy and neutrosophic sets [46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62].

Harish [16] proposed and analyzed an extension of the score function by incorporating hesitance. The authors presented an algorithm for the function including qualitative examples. Jun et al. [17] discuss INSs in algebra of BCK/BCI. Mehmet [18] put forward for analyzing the concept of the interval cut set (ICS) and strong ICS (α, β, γ) of IVNSs with proof and examples. Also, there are other several extensions of NSs described in the literature including interval-valued bipolar neutrosophic sets [19], hesitant interval neutrosophic linguistic set [20], and interval neutrosophic hesitant fuzzy sets [21]; for more details of neutrosophic set and their extensions, we refer the reader to [22,23,24,25,26,27,28].

Among humanistic problems of computer science, finding the shortest path is one of the significant problems. Many of the algorithms existing for optimization assumed the edge weights as the absolute real numbers. Despite this, we need to deal inexplicit parameters such as scope, costs, time and requirements in real-world problems. For example, a substantial length of any road is permanent; still, traveling time along the road varies according to weather and traffic conditions. An uncertain fact of those cases directs us to adopt fuzzy logic, fuzzy numbers, intuitionistic fuzzy and so on. The SPP using fuzzy numbers is called fuzzy shortest path problem (FSPP). Several researchers are paying attention in fuzzy shortest path (FSP) and intuitionistic FSP algorithms.

Das and De [29] employed Bellman dynamic programming problem for solving FSP based on value and ambiguity of trapezoidal intuitionistic fuzzy numbers. De and Bhincher [30] have studied the FSP in a network under triangular fuzzy number (TFN) and trapezoidal fuzzy number (TpFN) using two approaches such as influential programming of Bellman and linear programming with multi-objective. Kumar et al. [31] proposed a model to find the SP of the network under intuitionistic trapezoidal fuzzy number based on interval value. Meenakshi and Kaliraja [32] formulated interval-valued FSPP for interval-valued type and developed a technique to solve SPP.

Elizabeth and Sujatha [33] solved FSPP using interval-valued fuzzy matrices. Based on traditional Dijkstra algorithm, Enayattabar et al. [34] solved SPP in the interval-valued pythagorean fuzzy setting. Dey et al. [35] formulated fuzzy shortest path problem with interval type 2 fuzzy numbers. But, if the indeterminate information has appeared, all these kinds of shortest path problems failed. For this reason, some new approaches have been developed using neutrosophic numbers. Then neutrosophic shortest path was first developed by Broumi et al. [36]. The authors in [36] constructed an extension of Dijkstra algorithm to solve neutrosophic SPP. Then they used the extended version to treat the NSPP where the edge weight is characterized by IVNNs [37].

Broumi et al. [38,39,40] first introduced a technique of finding SP under SV-trapezoidal and triangular fuzzy neutrosophic environment. In [41], the authors proposed another approach to solve SPP on a network using trapezoidal neutrosophic numbers. Broumi et al. [42] developed a new algorithm to solve SPP using bipolar neutrosophic setting. In another paper, Broumi et al. [43] discussed an algorithmic approach based on a score function defined in [44] for solving NSPP on a network with IVNN as the edges. Liu and You proposed interval neutrosophic Muirhead mean operators and their applications in multiple-attribute group decision-making [45]. Thus, several papers are published in the field of neutrosophic sets [46,47,48,49,50,51,52,53,54,55]. Table 1 summarizes some contributions towards NSPP. Based on the idea of Bellman’s algorithm, SPP is solved for fuzzy network [29,30,31,32]. This algorithm is not applied yet on neutrosophic network. Therefore, there is a need to establish a neutrosophic version of Bellman’s algorithm for neutrosophic shortest path problems.

Table 1 Authors’ contributions towards neutrosophic shortest path problem
Full size table

The main motivation of this study is to introduce an algorithmic approach for SPP in an uncertain environment which will be simple enough and effective in real-life problem. The main contributions of this paper are as follows.

  • We concentrate on a NSP on a neutrosophic graph in which an IVNN, instead of a real number/fuzzy number, is assigned to each arc length.

  • A modified Bellman’s algorithm is introduced to deal the shortest path problem in an uncertain environment.

  • Based on the idea discussed in [15], we use an addition operation for adding the IVNNs corresponding to the edge weights present in the path. It is used to find the path length between source and destination nodes. We also use a ranking method to choose the shortest path associated with the lowest value of rank.

In this work, we are motivated to solve SPP by introducing a new version of BA where the edge weight is represented by IVNNs. The remaining part of the paper is presented as follows. The next section contains a few of the ideas and theories as overview of interval neutrosophic set followed by which the Bellman algorithm is discussed. In the subsequent section, an analytical illustration is presented, where our algorithm is applied. Then contingent study has been done with existing methods. Before the concluding section, advantages of the proposed algorithm are presented. Finally, conclusive observations are given.

Overview on interval-valued neutrosophic set

In this part, we recall few primary notions pertaining to NSs, SVNSs, IVNSs and some existing ranking functions for IVNNs which are the background of this study and will help us to further research.

Definition 1 [13]

Let X be a set of elements and its universal elements denoted by x; we define the neutrosophic set A (NS A) by A = {< x: \( T_{A} (x) \), \( {I_{A}} (x) \), \( {F_{A}} {(x)} \) > , x\( \in \)X}, where the functions T, I, F: X → ]−0,1+[ are called the truth, indeterminate and false MS functions, respectively, and they satisfy the following condition:

$$ ^{ - } 0 \, \le T_{A} (x) + I_{A} (x) + F_{A} (x) \le 3^{ + } . $$
(1)

The values of the three MS functions are taken from ]−0,1+[. As we have difficulty of applying NSs to real-time issues, Wang et al. [14] put forward the approach of a SVNS, which is the simplification of a NS and can be applied to any real-world topic.

Definition 2 [14]

\( \dddot A \) is the SVNS in X and is described by the set:

$$ \dddot A = \left\{ {\left\langle {x:T_{\dddot A} \left( x \right),I_{\dddot A} \left( x \right),F_{\dddot A} \left( x \right)} \right\rangle ,\,\,x \in X} \right\}, $$
(2)

where \( T_{\dddot A} \left( x \right),I_{\dddot A} \left( x \right),F_{\dddot A} \left( x \right) \in \left[ {0,{ 1}} \right] \) satisfying the condition:

$$ 0 \le T_{A} (x) + I_{A} (x) + F_{A} (x) \le 3. $$
(3)

Definition 3 [15]

An IVNS in X, which represented by:

$$ \dddot A = \left\{ {\langle {x:\tilde{T}_{\dddot A} \left( x \right),\tilde{I}_{\dddot A} \left( x \right),\tilde{F}_{\dddot A} \left( x \right)} \rangle ,x \in X} \right\}, $$
(4)
$$ \dddot A = \left\{ { \langle x:[T_{\dddot A}^{L} \left( x \right),T_{\dddot A}^{U} \left( x \right)\left] {,[I_{\dddot A}^{L} \left( x \right),I_{\dddot A}^{U} \left( x \right)} \right],[F_{\dddot A}^{L} \left( x \right),F_{\dddot A}^{U} \left( x \right)]\rangle ,x \in X} \right\}, $$
(5)

where \( [T_{\dddot A}^{L} \left( x \right),T_{\dddot A}^{U} \left( x \right)\left] {, [I_{\dddot A}^{L} \left( x \right),I_{\dddot A}^{U} \left( x \right)} \right], [F_{\dddot A}^{L} \left( x \right),F_{\dddot A}^{U} (x)] \subseteq [0,\;1] \) are the interval numbers satisfying the condition:

$$ 0 \le \sup T_{A} (x) + \sup I_{A} (x) + \sup F_{A} (x) \le 3. $$
(6)

Now we consider a few mathematical operations on interval-valued neutrosophic numbers (IVNNs)s.

Definition 4 [15]

Let

$$ \dddot A = \left\langle {\left[ {T_{a}^{L} ,T_{a}^{U} } \right],\left[ {I_{a}^{L} ,I_{a}^{U} } \right],\left[ {F_{a}^{L} ,F_{a}^{U} } \right]} \right\rangle \;{\text{and}}\;\dddot B = \left\langle {\left[ {T_{b}^{L} ,T_{b}^{U} } \right],\left[ {I_{b}^{L} ,I_{b}^{U} } \right],\left[ {F_{b}^{L} ,F_{b}^{U} } \right]} \right\rangle , $$

be two IVNNs and \( \eta > 0 \).

Then

$$ \dddot A \oplus \dddot B = \left\langle {\left[ {T_{a}^{L} + T_{b}^{L} - T_{a}^{L} T_{b}^{L} ,T_{a}^{U} + T_{b}^{U} - T_{a}^{U} T_{b}^{U} } \right],\left[ {I_{a}^{L} I_{b}^{L} ,I_{a}^{U} I_{b}^{U} } \right],\left[ {F_{a}^{L} F_{b}^{L} ,F_{a}^{U} F_{b}^{U} } \right]} \right\rangle , $$
(7)
$$ \dddot A \otimes \dddot B = \left\langle {\left[ {T_{a}^{L} T_{b}^{L} ,T_{a}^{U} T_{b}^{U} } \right],} \right.\left[ {I_{a}^{L} + I_{b}^{L} - I_{a}^{L} I_{b}^{L} ,I_{a}^{U} + I_{b}^{U} - I_{a}^{U} I_{b}^{U} } \right]\left. {\left[ {F_{a}^{L} + F_{b}^{L} - F_{a}^{L} F_{b}^{L} ,F_{a}^{U} + F_{b}^{U} - F_{a}^{U} F_{b}^{U} } \right]} \right\rangle , $$
(8)
$$ \eta \dddot A = \left\langle {\left[ {1 - \left( {1 - T_{a}^{L} } \right)^{\eta } ,1 - \left( {1 - T_{a}^{U} } \right)^{\eta } } \right],\left[ {\left( {I_{a}^{L} } \right)^{\eta } ,\left( {I_{a}^{U} } \right)^{\eta } } \right],\left[ {\left( {F_{a}^{L} } \right)^{\eta } ,\left( {F_{a}^{U} } \right)^{\eta } } \right]} \right\rangle , $$
(9)
$$ \dddot A^{\eta } = \left\langle {\left[ {\left( {T_{a}^{L} } \right)^{\eta } ,\left( {T_{a}^{U} } \right)^{\eta } } \right],\left[ {1 - \left( {1 - I_{a}^{L} } \right)^{\eta } ,1 - \left( {1 - I_{a}^{U} } \right)^{\eta } } \right],\left[ {1 - \left( {1 - F_{a}^{L} } \right)^{\eta } ,1 - \left( {1 - F_{a}^{U} } \right)^{\eta } } \right]} \right\rangle , $$
(10)

where \( \eta > 0. \)

Deneutrosophication formulas for interval-valued neutrosophic numbers

To compare two IVNNs \( \dddot A_{1} \) and \( \dddot A_{2} \), a map from [N (R)] to real line called score function has been used here. In the review of the literature, there are some formulas for deneutrosophication; in this paper, the following formulas have been focused [44, 45] and defined as follows:

$$ S_{\text{Ridvan }} \left( {\dddot A_{1} } \right) = \left( {\frac{1}{4}} \right) \times \left[ {2 + T_{x}^{L} + T_{x}^{U} - 2I_{x}^{L} - 2I_{x}^{U} - F_{x}^{L} - F_{x}^{U} } \right], $$
(11)
$$ S_{\text{Liu}} \left( {\dddot A_{1} } \right) = \left[ {2 + \frac{{T_{x}^{L} + T_{x}^{U} }}{2} - \frac{{I_{x}^{L} + I_{x}^{U} }}{2} - \frac{{F_{x}^{L} + F_{x}^{U} }}{2}} \right]. $$
(12)

Using score function (SF), the ranking technique is defined as below:

  1. (i)

    \( \dddot A_{1} < \dddot A_{2} \) if \( {\text{SF}}(\dddot A_{1} ) < {\text{SF}}(\dddot A_{2} ). \)

  2. (ii)

    \( \dddot A_{1} > \dddot A_{2} \) if \( {\text{SF}}(\dddot A_{1} ) > {\text{SF}}(\dddot A_{2} ). \)

  3. (iii)

    \( \dddot A_{1} = \dddot A_{2} \) if \( {\text{SF}}(\dddot A_{1} ) = {\text{SF}}(\dddot A_{2} ). \)

Computation of the shortest path based on neutrosophic numbers

In this section, the new algorithmic approach to solve IVNSP is provided. It is pretended that there are \( n \) nodes with the source node (SN), node 1 and destination node (DN), node n. The neutrosophic length between nodes \( i \) and \( j \) is denoted by \( d_{ij} \) and the set of all nodes having a connection with the node \( i \) is denoted by \( M_{N\left( i \right)} \).

Mathematical formulation of BELLMAN dynamic programming

Consider a directed connected graph \( G = \left( {V,E} \right) \) from SN ‘1’ and the DN ‘n’ which is acyclic and they are organized by topological ordering \( \left( {E_{ij} ;\,i < j} \right) \). Using the Bellman powerful programming system, the shortest path can be determined by forward pass computation method. The Bellman powerful programming system is defined as follows:

$$ f\left( i \right) = \left\{ {\begin{array}{*{20}c} {0,} & {i = 1} \\ {\mathop {\hbox{min} }\limits_{i < j} \left[ {f\left( i \right) + d_{ij} } \right],} & {\text{otherwise}} \\ \end{array} } \right., $$
(13)

where \( d_{ij} \) is the weight the directed edge \( E_{ij} \), \( f\left( i \right) \) is the length of SP node i from the SN 1.

Neutrosophic Bellman–Ford algorithm:

figure a

In the posterior section, we present a simple illustration to show the brevity of our method.

Illustrative example

This part is based on a numerical problem adapted from [43] to show the potential application of the proposed algorithm.

Example 1

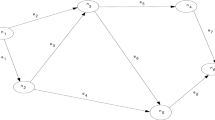
Consider an interval-valued neutrosophic network whose edge weights are represented by IVNNs with SN, node 1 and DN, node 6 (Fig. 1). Table 2 represents interval-valued neutrosophic distance.

Fig. 1
figure 1

Interval-valued neutrosophic network

Full size image
Table 2 The details of edge information in terms of interval-valued neutrosophic numbers
Full size table

Here we need to find the shortest distance from node 1 to node 6 (Table 3).

Table 3 The details of deneutrosophication value of edge (i, j)
Full size table

Using the proposed algorithm in previous section, the SP from SN and DN is calculated as follows:

$$ {{f}}\left( 1\right) = 0, $$
$$ {{f}}\left( 2\right) = \mathop {\hbox{min} }\limits_{i < 2} \left\{ {f\left( 1 \right) + c_{12} } \right\} = c_{12}^{*} = 0, 1 , $$
$$ {{f}}\left( 3\right) = \mathop {\hbox{min} }\limits_{i < 3} \left\{ {f\left( i \right) + c_{i3} } \right\} = \hbox{min} \left\{ {f\left( 1 \right) + c_{13} ,f\left( 2 \right) + c_{23} } \right\} = \left\{ {0 + 0, 1 7 5,0, 1+ 0, 2 3 5} \right\} = \left\{ {0, 1 7 5,0, 3 3 5} \right\} = 0, 1 7 5 , $$
$$ {{f}}\left( 4\right) = \mathop {\hbox{min} }\limits_{i < 4} \left\{ {f\left( i \right) + c_{i4} } \right\} = \hbox{min} \left\{ {f\left( 3 \right) + c_{34} } \right\} = \left\{ {0, 1 7 5+ 0,0 5} \right\} = 0, 2 2 5 , $$
$$ {{f}}\left( 5\right) = \mathop {\hbox{min} }\limits_{i < 5} \left\{ {f\left( i \right) + c_{i5} } \right\} = \hbox{min} \left\{ {f\left( 2 \right) + c_{25} ,f\left( 3 \right) + c_{35} } \right\} = \left\{ {0. 1+ 0, 1 2 5,0, 1 7 5+ 0, 4 5 5} \right\} = \left\{ {0. 2 2 5,0, 6 2 5} \right\} = 0. 2 2 5 , $$
$$ {{f}}\left( 6\right) = \mathop {\hbox{min} }\limits_{i < 6} \left\{ {f\left( i \right) + c_{i6} } \right\} = \hbox{min} \left\{ {f\left( 4 \right) + c_{46} ,f\left( 5 \right) + c_{56} } \right\} = \left\{ {0. 2 2 5+ 0, 3 5,0, 2 2 5+ 0, 1 2 5} \right\} = \left\{ {0. 5 7 5,0, 3 50} \right\} = 0. 3 50, $$

thus

$$ {f}\left( 6\right) = f\left( 5 \right) + c_{56} = f\left( 2 \right) + c_{25} + c_{56} = f\left( 1 \right) + c_{12} + c_{25} + c_{56} = c_{12} + c_{25} + c_{56} . $$

Therefore, the path P: 1 → 2 → 5 → 6 is recognized as the neutrosophic shortest path, and the crisp shortest path is 0.35.

Contingent study

In this section, the analysis of contingency for the proposed algorithm with existing approaches has been analyzed. A comparison of the results between the existing and new technique is shown in Table 4.

Table 4 Comparison of the sequence of nodes using neutrosophic shortest path and our proposed algorithm
Full size table

From the result, it is shown that the introduced algorithm contributes sequence of visited nodes which shown to be similar to neutrosophic shortest path presented in [43].

The neutrosophic shortest path (NSP) remains the same, namely 1 → 2 → 5 → 6, but the neutrosophic shortest path length (NSPL) differs, namely \( \left( {\left[ {0.424, 0.608} \right], \left[ {0.012, 0.06} \right], \left[ {0.016, 0.125} \right]} \right), \) respectively. From here we come to the conclusion that there exists no unique method for comparing neutrosophic numbers and different methods may satisfy different desirable criteria.

Advantages and limitations of the proposed algorithm

Advantages

By correlating our PA with Broumi et al. [43] to solve the same problem, we conclude that the proposed approach leads to the same path 1 → 2 → 5 → 6. The extended Bellman’s algorithm operates on neutrosophic directed graphs with negative weight edges whereas the extended Dijkstra algorithm proposed in [37] cannot deal with. This approach can be easily extended and applied to other neutrosophic networks with the edge weight as

  1. 1.

    Single-value neutrosophic numbers.

  2. 2.

    Bipolar neutrosophic numbers.

  3. 3.

    Trapezoidal neutrosophic numbers.

  4. 4.

    Cubic neutrosophic numbers.

  5. 5.

    Interval bipolar neutrosophic numbers.

  6. 6.

    Triangular neutrosophic numbers and so on.

Limitations

  1. 1.

    Slow response will be observed when there is a change in the network as this change will spread node-by-node.

  2. 2.

    If node failure occurs then routing loops may exist.

Conclusion

In this study, we describe the NSP, where edge weights are represented by IVNS. The advantage of using IVNSs in NSP is discussed in this paper. The classical Bellman’s algorithm is modified by incorporating the uncertainty using IVNSs for NPP between source and destination nodes. We use a numerical example to illustrate the efficiency of our proposed algorithm. The main goal of this work is to describe an algorithm for NSP in the neutrosophic environment using IVNS as edge weight. The proposed algorithm is very effective for real-life problem. In this paper, we have used a simple numerical example to illustrate our proposed algorithm. Therefore, as future work, we need to consider a large-scale practical shortest path problem using our proposed algorithm and to compare our proposed algorithm with the existing algorithm in terms of strictness of optimality, efficiency, computational time, and other aspects.