Transformation of solar wind energy into the energy of magnetospheric processes

Abstract

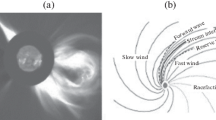
When the solar wind flows round the magnetosphere, its flow structure and interplanetary magnetic field lines are affected. This indicates the appearance of an electric current system in near-Earth space. the magnetized solar wind plasma moving at the solar wind velocity in the coordinate system of near-earth bow shock induces an electric field in this system. When crossing the bow shock front at the nose point, the tangential magnetic field component increases nearly four times, and the magnetic field energy density—15 times.

This paper relies on the results of earlier researches (Ponomarev et al. 2006a, 2006b), where we obtained the expression for electric current generated in the bow shock front and closed through the magnetosphere, as well as finding the magnetopause potential as a function of solar wind parameters—solar wind velocity and B _z -component of the interplanetary magnetic field. The power W consumed by the magnetosphere is equal to the Poynting flux through the magnetopause. According to a special case of Poynting’s theorem, applied to the geomagnetosphere, the energy flux can be expressed through electric potential (integration is over the entire magnetospheric surface). Thus, we obtain the required dependence for W. This dependence appears to be a square law relative to IMF B _z -component.

Appendix: Parabolic system of coordinates; in terms of Madelung (1957, 1960)

• In general case:

  $$\frac{u + iv}{\sqrt{2}} = \sqrt{z + i\rho}\quad \bigl(\rho = \sqrt{x^{2} + y^{2}}\bigr) $$
  $$u^{2} = r + z,\quad \mbox{where}\ r = \sqrt{z^{2} + \rho^{2}},\ x = uv\cos (\varphi ),\ 0 \le u \le \infty $$
  $$v^{2} = r - z,\qquad y = uv\sin (\varphi ),\quad 0 \le v \le \infty $$
  $$\varphi = \arctan \frac{y}{x},\qquad z = \frac{u^{2} - v^{2}}{2},\quad 0 \le \varphi \le 2\pi $$
  $$\rho = uv,\qquad r = \frac{u^{2} + v^{2}}{2},\qquad\frac{\partial u}{\partial \rho} = \frac{1}{2u}\frac{\rho}{r},\qquad \frac{\partial v}{\partial p}=\frac{1}{2v}\frac{\rho}{r},\qquad \frac{\partial u}{\partial z} = \frac{\partial v}{\partial \rho}. $$

• Linear element:

  $$ds^{2} = \bigl(u^{2} + v^{2}\bigr) \bigl(du^{2} + dv^{2}\bigr) + u^{2}v^{2}d \varphi^{2}. $$
  $$D = \frac{1}{u^{2} + v^{2}} = \frac{1}{2r}. $$

• Element of volume:

  $$dV = uv\bigl(u^{2} + v^{2}\bigr)dudvd\varphi. $$

• Vector components:

  $$a_{u} = \frac{a_{x}x + a_{y}y}{\sqrt{2r(r + z)}} + a_{z}\sqrt{\frac{r + z}{2r}},\qquad a_{x} = \frac{a_{u}v + a_{v}u}{\sqrt{u^{2} + v^{2}}} \cos (\varphi ) - a_{\varphi} \sin (\varphi ), $$
  $$a_{v} = \frac{a_{x}x + a_{y}y}{\sqrt{2r(r - z)}} - a_{z}\sqrt{\frac{r - z}{2r}},\qquad a_{y} = \frac{a_{u}v + a_{v}u}{\sqrt{u^{2} + v^{2}}} \sin (\varphi ) + a_{\varphi} \cos (\varphi ), $$
  $$a_{\varphi} = \frac{ - a_{x}y + a_{y}x}{\sqrt{x^{2} + y^{2}}},\qquad a_{z} = \frac{a_{u}u - a_{v}v}{\sqrt{u^{2} + v^{2}}}. $$

  Then:

  $$\operatorname{grad}_{u}\psi = \frac{1}{\sqrt{u^{2} + v^{2}}} \frac{\partial \psi}{\partial u},\qquad \operatorname{grad}_{v}\psi = \frac{1}{\sqrt{u^{2} + v^{2}}} \frac{\partial \psi}{\partial v},\qquad \operatorname{grad}_{\varphi} \psi = \frac{1}{uv}\frac{\partial \psi}{\partial \varphi} $$
  $$\operatorname{div}\mathrm{A} = \frac{1}{\sqrt{u^{2} + v^{2}}} \biggl\{ \frac{1}{u} \frac{\partial}{\partial u}(ua_{u}) + \frac{1}{v}\frac{\partial}{\partial v}(va_{v}) + \sqrt{\frac{1}{u^{2}} + \frac{1}{v^{2}}} \frac{\partial a_{\varphi}}{\partial \varphi} + \frac{ua_{u} + va_{v}}{u^{2} + v^{2}} \biggr\} , $$
  $$\Delta \psi = \frac{1}{u^{2} + v^{2}} \biggl\{ \frac{1}{u}\frac{\partial}{ \partial u} \biggl(u\frac{\partial \psi}{\partial u}\biggr) + \frac{1}{v}\frac{\partial}{\partial v}\biggl(v \frac{\partial \psi}{\partial v}\biggr) + \biggl( \frac{1}{u^{2}} + \frac{1}{v^{2}} \biggr) \frac{\partial^{2}\psi}{ \partial \varphi^{2}} \biggr\} $$
  $$\operatorname{curl}_{u}A = \frac{1}{v\sqrt{u^{2} + v^{2}}} \frac{\partial}{\partial v}(va_{\varphi} ) - \frac{1}{uv}\frac{\partial a_{v}}{\partial \varphi}, $$
  $$\operatorname{curl}_{v}A = \frac{1}{uv}\frac{\partial a_{u}}{\partial \varphi} - \frac{1}{u\sqrt{u^{2} + v^{2}}} \frac{\partial}{\partial u}(ua_{\varphi} ), $$
  $$\operatorname{curl}_{\varphi} A = \frac{1}{\sqrt{u^{2} + v^{2}}} \biggl\{ \biggl( \frac{\partial a_{v}}{\partial u} - \frac{\partial a_{u}}{\partial v} \biggr) + \frac{ua_{v} - va_{u}}{u^{2} + v^{2}} \biggr\} $$