Topology optimization analysis based on the direct coupling of the boundary element method and the level set method

Abstract

The structural design must ensure suitable working conditions by attending for safe and economic criteria. However, the optimal solution is not easily available, because these conditions depend on the bodies’ dimensions, materials strength and structural system configuration. In this regard, topology optimization aims for achieving the optimal structural geometry, i.e. the shape that leads to the minimum requirement of material, respecting constraints related to the stress state at each material point. The present study applies an evolutionary approach for determining the optimal geometry of 2D structures using the coupling of the boundary element method (BEM) and the level set method (LSM). The proposed algorithm consists of mechanical modelling, topology optimization approach and structural reconstruction. The mechanical model is composed of singular and hyper-singular BEM algebraic equations. The topology optimization is performed through the LSM. Internal and external geometries are evolved by the LS function evaluated at its zero level. The reconstruction process concerns the remeshing. Because the structural boundary moves at each iteration, the body’s geometry change and, consequently, a new mesh has to be defined. The proposed algorithm, which is based on the direct coupling of such approaches, introduces internal cavities automatically during the optimization process, according to the intensity of Von Mises stress. The developed optimization model was applied in two benchmarks available in the literature. Good agreement was observed among the results, which demonstrates its efficiency and accuracy.

Introduction

The structural engineer aims at attaching two targets that are normally, opposite: safety and economy. In the most part of structural designs, the optimal solution, i.e. the solution that couples perfectly such targets, is not easily available because it depends on the material characteristic strengths, structural dimensions and structural system adopted. To solve consistently such engineering challenge problem, special theories/techniques have recently emerged (Bendsøe and Kikuchi 1988; Rozvany et al. 1992; Maute and Ramm 1995). Among them, it is worth mentioning the topology optimization. This domain aims for designing the geometry of structural components with proper safety level accounting for the minimum requirement of material. Thus, this type of optimization achieves the optimal structural geometry, the shape that leads to the minimum requirement of material, respecting constraints related to the stress state at each material point.

The mechanical modelling of structures may be accomplished through analytical approaches, which are normally based on the theory of elasticity. However, the solutions provided by this theory are limited to simplified geometries, boundary conditions and material constitutive relations. Thus, to enable a general mechanical modelling numerical methods are required. The present study utilized the boundary element method (BEM), which is recognized as a robust and efficient numerical technique. The BEM is capable for handling accurately several types of mechanical problems. Due to its mesh dimension reduction and accuracy in determining stress concentration fields, the BEM becomes well adapted for solving topology optimization problems.

The topology optimization was initially proposed in the end of 1980s by Bendsøe (1989), which analysed the material distribution into a fixed domain. The optimal structural geometry was achieved through the definition of a material density, which may vary from a void until the full presence of material. An intermediate material density may be also assumed. The bubble method was introduced by Eschenauer et al. (1994), which is based on the insertion of cavities in the structure and the subsequent use of the shape optimization method for determining the optimal structural size and shape. The simpler evolutionary structural optimization (ESO) method, presented by Xie and Steven (1993), removes material progressively from low stress regions based on a given acceptation/rejection criteria. This technique was widely applied with finite element models due to the domain mesh required in such models.

Topology optimization analyses in two- and three-dimensional structures using the BEM are presented in Cervera and Trevelyan (2005a, b). In their ESO approach, the moving structural geometry was represented explicitly through the NURBS, in which the spline control points is moved according to the response of local stress values. The boundary element-based topological derivatives concept was used for the first time by Marczak (2007), for the topology optimization of thermally conducting solids. The proposed formulation was based on introducing an iterative material removal procedure in a BEM framework. Topology optimization in 2D elastic structures through the BEM is presented in Neches and Cisilino (2008). Linear boundary elements were adopted and small cavities are inserted around internal points with the lowest values of the topological derivative. The topology optimization in a 3D BEM elastostatic framework taking into account the topological shape sensitivity method for the direct calculation of topological derivatives from stress fields is introduced in Bertsch et al. (2010). The shape derivatives were combined with topological derivatives by Allaire and Jouve (2008), to propose a level set-based optimization method capable for automatic hole insertion.

An efficient approach in the topology optimization domain consists of the level set method (LSM). This method was proposed, initially, to model the movement of curves (Osher and Sethian 1988; Sethian 1999). When the LSM is applied in the structural context, the mentioned curves represent the structural boundary and its movement/evolution characterizes the new/optimized structural geometry. The LSM is based on the solution of Hamilton–Jacobi differential equations. The LSM represents the structural geometry as well as its evolution through the zero level of an important function denominated level set (LS) (Osher and Sethian 1988; Sethian 1999; Shichi et al. 2012; Yamada et al. 2013; Osher and Fedkiw 2003).

In the present study, the topology optimization analysis is developed accounting for the direct coupling of BEM–LSM. The proposed algorithm consists of three parts: mechanical modelling, topology optimization procedure and structural reconstruction. The mechanical modelling is accomplished through the BEM algebraic equations, in which singular and hyper-singular integral representations may be applied.

The singular integral equation represents accurately the mechanical material behaviour in the most part of elastostatic problems. However, the application of this integral equation for source points nearly positioned may lead to the singularities on the final system of algebraic equations due to the singular nature of the fundamental solutions. Such singularities are avoided using the hyper-singular integral equation in addition to the first mentioned integral equation. During the topology evolution process, complex geometries may appear leading to nearly positioned source points. Thus, in this study, the singular and hyper-singular integral equations are utilized into the discretization in order to provide numerical stability, which is one contribution of this study.

The topology optimization procedure is performed using the LSM approach. The structural geometry is described by the LS function evaluated at its zero level. The velocities of moving boundaries are determined according to the Von Mises stress intensity at each boundary node. The coupling between the LSM and the Von Mises stresses provided by BEM is direct. Thus, velocity extension scheme is not required, which is another contribution of this study.

Finally, the reconstruction process concerns the remeshing procedure. Because the boundary moves at each iteration, the structural geometry change and a new mesh has to be constructed. The new mesh is proposed accounting for the source points position. Then, singular and hyper-singular integral equations are proper applied. During the topology optimization process, internal cavities may be introduced automatically, in order to accelerate the numerical convergence. The internal cavities are punctually included where the Von Mises stress is lower than an established threshold. The boundaries of such cavities may grow or collapse according to the Von Mises stress. This is one advantage of LSM, in which material may be removed or include in automatic and in consistent form.

Two applications are presented in the present study to illustrate the relevance of the presented framework. The results obtained by the presented scheme are in good agreement with the responses provided by the literature.

The boundary element method

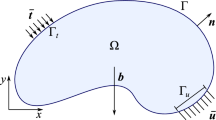
The BEM has been widely utilized in engineering fields such as contact mechanics and fracture mechanics due to its high accuracy and robustness in modelling strong stress concentration. In addition to this inherent ability of the BEM, its mesh dimension reduction makes this numerical method well adapted to solve topology optimization problems. The integral equations required by the BEM are obtained from the equilibrium equation. Considering a 2D homogeneous elastic domain, $\varOmega$, with boundary, $\varGamma$, the equilibrium equation, written in terms of displacements, is given by

$$u_{i,jj} + \frac{1}{1 - 2\upsilon }u_{j,ji} + \frac{{b_{i} }}{\mu } = 0$$

(1)

in which $\mu$ is the shear modulus, $\upsilon$ is the Poisson’s ratio, $u_{i}$ are the components of the displacement field, and $b_{i}$ are the body forces.

Afterwards, the Betti’s theorem is utilized and the singular integral representation, written in terms of displacements, is obtained (without body forces) as follows:

$$c_{ij} (s,f)u_{j} (s) + \int\limits_{\varGamma }^{{}} {P_{ij}^{*} (s,f)u_{j} (f){\text{d}}\varGamma } = \int\limits_{\varGamma }^{{}} {U_{ij}^{*} (s,f)p_{j} \left( f \right){\text{d}}\varGamma }$$

(2)

in which $p_{j}$ and $u_{j}$ are tractions and displacements at the field points $f$, respectively, the free term $c_{ij}$ is equal to ${\raise0.7ex\hbox{${\delta_{ij} }$} \!\mathord{\left/ {\vphantom {{\delta_{ij} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}$ for smooth boundaries and $P_{ij}^{*}$ and $U_{ij}^{*}$ are the fundamental solutions for tractions and displacements written for the source point $s$ (Brebbia and Dominguez 1992; Hong and Chen 1988).

The Eq. (2) has to be differentiated with respect to the directions x, y, in order to obtain an integral equation written in terms of strains. Then, the use of the generalized Hooke’s law leads to the integral representation of stresses for a boundary source point. Finally, the Cauchy formula has to be applied for obtaining the hyper-singular integral equation, which is written in terms of tractions as follows:

$$\frac{1}{2}p_{j} (s) + \eta_{i} \int\limits_{\varGamma }^{{}} {S_{ijk}^{*} (s,f)u_{k} (f){\text{d}}\varGamma } = \eta_{i} \int\limits_{\varGamma }^{{}} {D_{ijk}^{*} (s,f)p_{k} (f){\text{d}}\varGamma }$$

(3)

in which $S_{ijk}^{*}$ and $D_{ijk}^{*}$ contain the new kernels computed from $P_{ij}^{*}$ and $U_{ij}^{*}$, respectively, (Brebbia and Dominguez 1992; Hong and Chen 1988) and $\eta_{k}$ is the outward normal vector.

To assemble the system of BEM equations, as usual, Eq. (2) or Eq. (3) are transformed into algebraic relations by discretizing the structural boundary into elements over which displacements and tractions are approximated. In the present study, only linear discontinuous boundary elements are applied. The regular integrals were calculated using Gauss–Legendre quadrature whereas the singularity subtraction technique was applied in the integration over singular boundary elements. The discretization of external boundary into boundary elements leads to the following system of algebraic equations:

$$Hu = Gp$$

(4)

where $u$ and $p$ are vectors that contain displacements and tractions at the boundary source points, respectively. The matrix $H$ contains the terms evaluated numerically from the kernels $P_{ij}^{*}$ or $S_{ijk}^{*}$ whereas $G$ is composed by the terms calculated from the kernels $U_{ij}^{*}$ or $D_{ijk}^{*}$.

After determining the displacement and traction fields at the boundary, internal values for displacements, stresses and strains are achieved. Internal displacements are determined through the integral equation Eq. (2) with the source point positioned at the domain. In such case, the free term $c_{ij}$ becomes $\delta_{ij}$. On the other hand, the stress field at internal nodes is obtained through the integral representation of stresses (Brebbia and Dominguez 1992; Hong and Chen 1988).

The level set method

The LSM is a robust technique for simulating and for determining the movement of curves in different physical scenarios. Such method represents a particular curve (or surface) $\varGamma$ as well as its movement/evolution along time as the zero level of a major function $\varPhi$, which is denominated level set (LS) function. Figure 1 illustrates a classical example of one LS function. This figure illustrates the movement/evolution of a circle, which LS function is conical. The LS equation and its evolutions, for general cases, are represented in the following form:

$$\varPhi_{t} + \mathop V\limits^{ \to } \cdot \nabla \varPhi = 0$$

(5)

in which $\varPhi_{t}$ is the partial time derivative, $\mathop V\limits^{ \to }$ is the velocity field at the grid points and $\nabla \varPhi$ is the gradient of the $\varPhi$ function, which represents the gradient of the partial derivatives according to x and y directions.

Fig. 1

Level Set Function. Circle evolution due to a conical surface

By solving Eq. (5), through the finite differences for instance, the values of $\varPhi$ are determined for all points that belong to the domain analysed. Therefore, based on the $\varPhi$ values, the new structural boundaries are achieved. The LSM is capable of eliminating complexities of movement of curves such as singularities, weak solutions, shocks formation, non-stable conditions of entropy and topology changes that involve interfaces. In the context of numerical analysis, the LSM utilizes natural and accurate computational procedures. The method represents accurately corners and geometry ends as well as topology discontinuities.

Topology optimization by the direct coupling of BEM–LSM

As previously mentioned, the topology optimization analysis is developed based on the direct coupling of BEM–LSM. The developed numerical procedure consists of three parts: mechanical modelling, topology optimization procedure and structure reconstruction.

The mechanical modelling is accomplished by the BEM. The BEM requires the structural boundaries discretization by nodes and elements in order to determine stresses and displacements at the structural boundaries into the structural domain. The structural boundaries geometries are described through the LS function evaluated at its zero level. Then, the curve delimited by the LS function at its zero level is discretized into linear discontinuous boundary elements.

When the source points are nearly positioned into the BEM mesh, singularities at the final system of algebraic equations may appear. Such singularities occur due to the singular nature of the fundamental solutions required by the BEM. Thus, to avoid these types of singularities, singular and hyper-singular integral equations are utilized in the presented model. These integral equations are alternately utilized along the boundary mesh when the distance between a given source point and its closest source point is lower than 10% of the boundary element length that contains the given source point. It is worth mentioning that nearly positioned source points often appear in this problem, because the topology evolution procedure leads to the intermediate complex geometries before the convergence. Thus, the proposed scheme leads to the stable and accurate BEM responses.

An Eulerian mesh is required for solving the topology optimization problem, which is defined by a rectangular grid, Fig. 2. This mesh is responsible for approximating the LS function values along the entire design domain. Therefore, nil values for the LS function are observed at the structural boundaries. The LS values at the Eulerian grid points are evolved along the topology optimization procedure, similarly as presented in Yamasaki et al. (2012). The velocity criterion for evolving the structural boundaries is presented below. Then, the structural geometry is immersed into the Eulerian grid and the structural geometrical coordinates, which introduce nil LS values, become a part of such mesh. It is worth mentioning that the structural boundaries do not coincide, necessarily, with the Eulerian grid points because the structure is immersed into this grid. Thus, for each grid point, the LS function is determined. Initially, such function is defined as the orientated distance between the grid points and the structural boundary.

Fig. 2

Eulerian mesh and structural immersion

The Eulerian grid points positioned inside the boundary are represented by negative values of $\varPhi$. On the other hand, the positive values of $\varPhi$ indicate points positioned outside the boundary. Finally, nil value of $\varPhi$ defines the zero LS and, consequently, the structural boundary. Thus, the sign for $\varPhi$ function is written as presented in Eq. (6).

$$\begin{aligned} & \varPhi > 0\quad {\text{outer}}\; {\text{design}}\;{\text{domain}}\;{\text{points}} \hfill \\ &\varPhi = 0\quad {\text{boundary}}\;{\text{design}}\;{\text{points}} \hfill \\ & \varPhi < 0\quad {\text{inner}}\;{\text{design}}\;{\text{domain}}\;{\text{points}} \hfill \\ \end{aligned}$$

(6)

In this study, Eq. (5) is solved using the upwind differences method (Sethian 1999). This method calculates the partial derivatives of the LS function in relation to x and y directions. The time interval required by the method is considered as fictitious and the number of evolutions carried out at each iteration must be defined. Because $\varPhi_{t - 1}$ and $\varPhi$ are known at each Eulerian grid point, a velocity function $\mathop V\limits^{ \to }$ must be defined to enable the LS evolution process. The velocity function depends of the Von Mises stress values at each Eulerian grid point. Such dependence is consistent because the topology optimization is applied in solid mechanics problems (in potential problems the flux could derive the moving boundaries velocity, for instance). Thus, the objective of the topology optimization performed in this study is the determination of the structural geometry in which all structural material points have the same Von Mises stress values. As a result, the optimized structural material has the same stress state, which defines the fully stressed design approach and the maximum use of the mechanical material capacity. The Von Mises stress is presented in Eq. (7), which has to be evaluated for each Eulerian grid point.

$$\sigma_{\text{vm}} = \frac{1}{\sqrt 2 }\sqrt {(\sigma_{1} - \sigma_{2} )^{2} + (\sigma_{2} - \sigma_{3} )^{2} + (\sigma_{3} - \sigma_{1} )^{2} }$$

(7)

in which $\sigma_{1}$, $\sigma_{2}$ and $\sigma_{3}$ indicate the principal stresses.

The Von Mises stress is evaluated by the BEM at each grid point. Therefore, inefficient structural material is progressively removed as well as required structural material is added where necessary. Such regions are determined naturally through the evolution of the LS function. To define the velocity function for moving boundaries according to the intensity of the Von Mises stress, stress intervals are required. Thus, a heuristic approach is utilized for governing the moving boundaries velocity. Such intervals are expressed as a function of $\sigma_{\text{vm}}$, ${\text{RR}}$, $\sigma_{y}$ and $\sigma_{\hbox{max} }$, which are the Von Mises stress, the removal rate, yield stress and maximum Von Mises stress, respectively. The velocity criteria adopted in this study, $V_{n}$, and recommended by Ullah et al. (2014), are presented in Eq. (8).

$$\begin{array}{*{20}l} {\sigma _{{{\text{vm}}}} \in \left[ {0,\sigma _{{t1}} } \right]:\sigma _{{t1}} = 0.5{\mkern 1mu} {\text{RR}}{\mkern 1mu} \sigma _{{{\text{max}}}} } \hfill & {V_{n} = - 1} \hfill \\ {\sigma _{{{\text{vm}}}} \in \left[ {\sigma _{{t1}} ,\sigma _{{t2}} } \right]:\sigma _{{t2}} = 0.9{\mkern 1mu} {\text{RR}}{\mkern 1mu} \sigma _{{{\text{max}}}} } \hfill & {V_{n} \in \left[ { - 1,0} \right]} \hfill \\ {\sigma _{{{\text{vm}}}} \in \left[ {\sigma _{{t2}} ,\sigma _{{t3}} } \right]:\sigma _{{t3}} = 0.95{\text{min}}(\sigma _{{{\text{max}}}} ,\sigma _{y} )} \hfill & {V_{n} = 0} \hfill \\ {\sigma _{{{\text{vm}}}} \in \left[ {\sigma _{{t3}} ,\sigma _{{t4}} } \right]:\sigma _{{t4}} = {\text{min}}(\sigma _{{{\text{max}}}} ,\sigma _{y} )} \hfill & {V_{n} \in \left[ {0,1} \right]} \hfill \\ {\sigma _{{{\text{vm}}}} \in \left[ {\sigma _{{t4}} ,\infty } \right]:} \hfill & {V_{n} = 1} \hfill \\ \end{array}$$

(8)

The negative velocities indicate point movement in the inner boundary direction. Thus, negative velocities are related to the removing material condition. Similarly, the point movement in the outer direction is related to positive velocities. In such condition, structural material is added. Nil velocity indicates non-movement for the points. The criterion presented in Eq. (8) is illustrated in Fig. 3.

Fig. 3

Variation of Von Mises stress versus velocity

Therefore, the moving boundaries are governed by the criterion described in Eq. (8). To improve the convergence rate, internal cavities are automatically introduced during the topology evolution. Such cavities are included in points where the Von Mises stress reaches a threshold value. The analyst defines the threshold value and just one cavity per iteration is allowed. In the present study, the cavity inclusion obeys the criterion defined in Eq. (9).

$$\sigma_{\text{vm}} < {\text{RR}}\,\sigma_{ \hbox{max} }$$

(9)

The cavity radius is equal to the minimum value between Δx and Δy, which are illustrated in Fig. 2. The cavity inclusion allows for faster convergence as the material is removed in regions with very low stress state. Then, the removing procedure is improved with the cavities inclusion. The cavity inclusion procedure is inspired in the classical ESO approaches. However, the scheme proposed in this study enables for adding material condition, when the material is removed in a non-proper region. This is an improvement over the classical ESO approaches in which hard-kill conditions are often utilized.

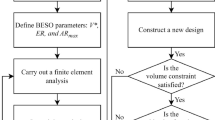
The direct coupling BEM–LSM requires an update mesh procedure. Because of the structural boundary change at each LSM iteration, the boundary mesh considered in the previous iteration must be eliminated and a new boundary mesh must be constructed at the new zero LS. Thus, a complex remeshing procedure must be performed. The developed remeshing algorithm is capable of recognizing the amount of curves present in the structure (outer and inner boundaries) and to achieve the zero LS as the final boundary. Such mapping procedure accounts for the LS values at each Eulerian grid point. Then, the zero LS is discretized into nodes and linear discontinuous boundary elements for further analysis of the BEM. This process is repeated until the desired optimal geometry be reached. To assist computational implementation by the reader, a flowchart is introduced and presented in Fig. 4.

Fig. 4

BEM–LSM scheme for 2D topology optimization

Examples

The direct BEM–LSM formulation presented in this study is applied in the topology optimization analysis of two structures. One tensile case and one bending case were chosen. In both analyses, the results obtained agree with the responses available in the literature.

Two bar truss problem

The first application of the presented direct BEM–LSM formulation concerns the topology optimization of the plane structure illustrated in Fig. 5. This structure is clamped along two regions at its left end and is subjected to a pointed load positioned at the middle of its right end. The material properties utilized for this analysis are the following: Young’s modulus $E = 210\,\,{\text{GPa}}$, Poisson ratio $\upsilon = 0,3$ and material yield stress $\sigma_{y} = 280\,{\text{MPa}}$.

Fig. 5

Structure analysed. Dimensions in metre

The reduction factor utilized in this analysis is equal to ${\text{RR}} = 0.10$. Moreover, 10 evolutions for each time step into the upwind difference method were applied. The fictitious time used is $\Delta t = 0.003$. The Eulerian mesh adopted for solving the problem is composed of a grid with $67\, \times \,45$ points. Thus, 3015 points compose the grid. The values of $\Delta x$ and $\Delta y$ are equal to $\Delta x = \Delta y = 0.10\,\,{\text{m}}$.

In this analysis, one aims to obtain the structural geometry that, after optimized, contains $40\%$ of the initial structural volume. Thus, the application of the direct BEM–LSM formulation leads to the geometry evolution presented in Fig. 6, which resembles a two-bar truss structure. The internal cavities were included during the evolution process and it accelerated the convergence process. Moreover, the symmetric aspects were kept and the result obtained agrees with classical references (Yamada et al. 2013; Ullah et al. 2014).

Fig. 6

Geometry evolution process

The evolutional behaviour of the structural area values during the iterative process is illustrated in Fig. 7. According to this figure, a smooth convergence is observed. It indicates the numerical stability of the developed procedure. Moreover, the horizontal parts in this figure, in iterations 12, 24 and 39, indicate the cavities insertion.

Fig. 7

Structural area evolution during the numerical procedure

The LS functions obtained during the evolution process are illustrated in Fig. 8. It is worth mentioning the geometrical complexity involved in such functions.

Fig. 8

LS functions and its evolutions during the optimization process

Finally, the LS function as well as its levels for the optimal geometry is illustrated in Fig. 9. The geometrical complexity involved in this LS must be mentioned, even for this simple application.

Fig. 9

LS functions and its levels for the optimised geometry

In addition, the stress state in the initial and the optimized structural geometries was analysed. Figure 10 presents the comparison, in which the Von Mises stresses are illustrated. One observes the better stress distribution in the optimized structural geometry, as expected.

Fig. 10

Comparison for Von Mises stress. Stress presented in kPa

Cantilever beam problem

The last application of the present study deals the topology optimization of the plane structure illustrated in Fig. 11. This is a cantilever beam, which is clamped at two regions along its left end and subjected to a vertical load positioned at its right upper corner. The material properties adopted for this topology optimization analysis are the following: Young’s modulus $E = 210\,\,{\text{GPa}}$, Poisson ratio $\upsilon = 0,3$ and material yield stress $\sigma_{y} = 280\,{\text{MPa}}$.

Fig. 11

Structure analysed. Dimensions in metre

The reduction factor adopted for carrying out the evolution process is equal to ${\text{RR}} = 0.25$. In addition to that, 5 evolutions for each time step into the upwind difference method were imposed. The fictitious time utilized is $\Delta t = 0.003$. The Eulerian mesh adopted for describing the LS function as well as its evolutions during the numerical procedure is composed of a grid with $67\, \times 45$ points. Therefore, the Eulerian mesh is composed of 3015 points. The values of $\Delta x$ and $\Delta y$, which are illustrated in Fig. 2, are assumed as $\Delta x = \Delta y = 0.10\,\,{\text{m}}$.

The goal in this numerical analysis is the accomplishment for the structural geometry topologically optimized that contains 40% of its initial volume. The direct BEM–LSM model is capable for achieving such goal. The structural geometry evolution obtained is presented in Fig. 12. The internal cavities appeared naturally during the evolution procedure and improved its convergence. Moreover, the result obtained by the presented direct BEM–LSM formulation agrees with the responses available in the literature (Yamada et al. 2013; Ullah et al. 2014).

Fig. 12

Geometry evolution process

The evolution of the structural area reduction during the iterative process is presented in Fig. 13. The smooth convergence is observed, which indicates the numerical stability of the developed procedure. In addition, the horizontal portions of the curve illustrated in this figure, in iterations 20 and 115, indicates the cavities insertion.

Fig. 13

Structural area evolution during the optimization procedure

The evolution of the LS functions achieved during the optimization procedure is illustrated in Fig. 14. It is worth mentioning the geometrical complexity of such functions.

Fig. 14

LS functions and its evolutions during the optimization procedure

Figure 15 illustrates the LS function and its levels for the optimal geometry, i.e. for the solution problem. The geometrical complexity involved in such an LS function must be mentioned.

Fig. 15

LS functions and its levels for the optimised geometry

The stress state in the initial and the optimized structural geometries was also analysed. Figure 16 illustrates this comparison, in which the Von Mises stresses are presented. As expected, the better stress distribution is observed in the optimized structural geometry.

Fig. 16

Comparison for Von Mises stress. Stress presented in kPa

Conclusion

In this study, the topology optimization analysis was accomplished in 2D structures through the direct coupling of BEM–LSM. In such coupled numerical model, the advantages of each method were utilized for obtaining the optimal structural geometry. Therefore, each method is utilized in an efficient and accurate manner. The BEM is applied accurately for determining stress values at the Eulerian grid points. In addition, the BEM requires only boundary discretization. Thus, this numerical model is well adapted for solving topology optimization problems, as both approaches (BEM and topology optimization) require information over the boundary for the moving boundaries solution problem. On the other hand, the LSM enables robustly for the curve motion modelling. Such approach is capable of handling accurately complex curve movements, which involves singularities, weak solutions, topology changes and interfaces.

Two applications were considered in this study. The results obtained in both cases are in good agreement with the solutions presented in the literature, which indicates the accuracy of the direct BEM–LSM formulation presented. Moreover, smooth and stable numerical convergence were observed, which indicates the numerical stability of the presented optimization scheme.

In spite of its accuracy and robustness, some developments are due in course in order to improve the developed model. Among them, it is worth mentioning the parallelization of the computational code. This development aims at improving the computational time consuming, which at this moment may restrict large industrial applications.