A multi-channel $\varvec{H}_\infty$ preview control approach to load alleviation design for flexible aircraft

Abstract

Gust load alleviation functions are mainly designed for two objectives: first, alleviating the structural loads resulting from turbulence or gust encounter, and hence reducing the structural fatigue and/or weight; and second, enhancing the ride qualities, and hence the passengers’ comfort. Whilst load alleviation functions can improve both aspects, the designer will still need to make design trade-offs between these two objectives and also between various types and locations of the structural loads. The possible emergence of affordable and reliable remote wind sensor techniques (e.g., Doppler LIDAR) in the future leads to considering new types of load alleviation functions as these sensors would permit anticipating the near future gusts and other types of turbulence. In this paper, we propose a preview control design methodology for the design of a load alleviation function with such anticipation capabilities, based on recent advancements on discrete-time reduced-order multi-channel $H_\infty$ techniques. The methodology is illustrated on the DLR Discus-2c flexible sailplane model.

1 Introduction

Turbulence and gusts are causing dynamic variations of the aerodynamic forces and moments that are applied to the aircraft structure. In addition to causing structural loads that the structure should be designed to support, the resulting motion causes passengers discomfort and anxiety. Active load alleviation of turbulence and gust is not a new topic: the analysis, synthesis, design, and flight testing of an advanced control system to alleviate gust loads and control structural modes of the Boeing B-52E during the Load Alleviation and Mode Stabilization (LAMS) program dates back 50 years [1]. Over the last decades, many gust load alleviation systems had been implemented on numerous airplanes, such as: Lockheed C-5A, Lockheed L-1011-500, Boeing B-1, Northrop Grumman B-2, Airbus A320, Airbus A330/A340, Airbus A380, Boeing 787, and Airbus A350 (see [2] and the references therein).

In [3], the authors synthesized an ${H_\infty }$ optimal controller for alleviating the structural loads and enhancing the ride qualities of a flexible aircraft. In their work, the controller was synthesized by two different methods of the ${H_\infty }$ optimal control: full-order based on the work of [4, 5], and fixed-structure based on the method presented in [6, 7], and implemented in the MATLAB Robust Control Toolbox. For better anticipation of the future turbulence or gust, and hence better controller performance, feedforward and feedback load alleviation functions were designed together. The formulation of the feedforward load alleviation is made with a preview control problem formulation that is similar to the approach of [8], but in output feedback setting and adapted to a different application. Their simulation results showed that the structural loads and the normal load factor at pilot location (a ride quality index) had been greatly reduced compared to the case of no control (i.e., open loop) and also to the case of feedback-only control. The same reduction had been successfully achieved by both the full-order and the fixed-structure $H_\infty$ optimal control synthesis methods.

However, the design of active load alleviation functions usually requires to perform complex trade-offs between the different types of loads across the airframe, as well as the comfort criteria at different locations within the cabin and in the cockpit. The mono-channel $H_\infty$ algorithms that were used in [3] forced combining all the design objectives into a one single performance channel, which led to including unwanted cross-coupling terms in the $H_\infty$ norm of the overall transfer function. Hence, this mono-channel formulation limits the control designers in expressing the control design criteria, which makes it difficult to perform the fine tuning needed when designing more complex load alleviation systems. The present work extends the problem formulation used in [3] using the multi-channel capabilities provided by the structured $H_\infty$ control techniques, instead of using the mono-channel approach. For conciseness reasons, only a two-channel example is shown in this paper for a trade-off between a passenger comfort criterion and a structural loads criterion. However, the principles and ideas presented remain the same for more complex cases with more channels.

The paper contains two main parts: first, the control design method is presented in a relatively generic way in Sect. 2; and second, an application to the design of a load alleviation function is presented in Sect. 3.

2 Using preview control for gust load alleviation

In this work, the optimal tuning of feedforward-enabled gust load alleviation controllers is investigated. The investigations shown in the present paper and in [3, 9] are a continuation of the work published in [10, 11] which focuses on optimizing the load alleviation controller(s). In [10, 11], the overall design problem for the Airbus XRF-1 configuration was presented. The feedforward part of the load alleviation functions in [10, 11] used a decomposition into several sub-functions, based on time-frequency decompositions of the forthcoming turbulence. Each of these sub-functions were fulfilled by simple controllers which were tuned manually. The work presented herein contributes to the development of more advanced and systematic control design methodologies for tuning either these sub-functions or the entire feedforward load alleviation function. The work uses multi-channel reduced-order $H_\infty$ control design techniques for synthesizing a combined preview-based feedforward and classical feedback gust load alleviation function, and applies it on a relatively simple example with only two channels. In practice, to tackle industry-size control design problems, a significantly larger number of channels would have to be defined; the methodology, however, would be the same as in the simple example shown hereafter.

2.1 Basics on $H_\infty$ control techniques

This section provides a very short introduction to $H_\infty$ control, with the aim of easing the reading of the rest of the paper by giving the non-specialist readers a general idea of these techniques. In spite of that, this introduction can by no means cover all the extensive literature on $H_\infty$ techniques. The concept of $H_\infty$ control has been introduced in the late 1970s and early 1980s. The standard $H_\infty$ problem formulation is illustrated in Fig. 1. This figure consists of a lower linear fractional transformation, with the system/plant P last outputs $\varvec{y}$ (measurements) being fed back to its last inputs $\varvec{u}$ (control commands), through a controller K. The performance channel inputs and outputs are represented by $\varvec{w}$ and $\varvec{z}$, respectively. The aim of the $H_\infty$ control design is to find a controller K which minimizes the $H_\infty$-norm (i.e., $\Vert ...\Vert _\infty$) of the transfer function $T_{\varvec{w}\rightarrow \varvec{z}}=F_l(P,K)$, and provides a stable closed loop. The term $H_\infty$ itself is derived from the corresponding Hardy space [12, 13], and can also be seen as a particular case of the $L_2$-induced norm in case of linear dynamic systems.

Fig. 1

Standard form for control synthesis

Controllers synthesized with $H_\infty$ techniques are often considered as “robust controllers” due to the use of the $H_\infty$-norm when applying the “small-gain theorem” to linear time-invariant (LTI) systems [12,13,14]. The basic idea of this theorem for the interconnection of Fig. 1 can be expressed as follows:

Let $\gamma = \Vert T_{\varvec{w}\rightarrow \varvec{z}}=F_l(P,K)\Vert _\infty$, and then, the performance channel outputs $\varvec{z}$ can be fed back to the performance channel inputs $\varvec{w}$, through any system $\varDelta$, such that $\Vert \varDelta \Vert _\infty <1/\gamma$, without destabilizing the closed loop $F_u ( F_l(P,K),\varDelta )$. As a consequence, if the performance channel inputs $\varvec{w}$ and outputs $\varvec{z}$ are chosen, such that closing the loop from $\varvec{z}$ to $\varvec{w}$ can be interpreted physically as taking a meaningful set of uncertainties into account, then minimizing the $H_\infty$-norm from $\varvec{w}$ to $\varvec{z}$ increases the robustness of the closed loop.

The small-gain theorem gives necessary and sufficient conditions for robust stability against unstructured uncertainties, but is often relatively conservative when dealing with structured uncertainties (no exploitation of the structure). In its basic formulation, it also provides no direct guaranty for robust performance in the presence of uncertainties (regardless of being structured or unstructured). Besides, the $H_\infty$ control design algorithms are often used to shape the response, or some transfer function, of the closed loop. It is important to understand that in those cases, the robustness of the closed loop is not necessarily increased, and can even be significantly reduced. With other words, $H_\infty$ techniques can be used to increase robustness, but the sole fact that $H_\infty$ techniques have been used does not mean that the obtained closed loop is robust: the achieved performance and the physical meaning of the defined performance channel(s) must be analyzed to be able to conclude on robustness.

In this paper, the $H_\infty$ techniques are only used to specify the desired load alleviation behavior (i.e., to shape the gust/turbulence disturbance rejection), with and without preview of disturbance. The solutions obtained were found to be quite robust, but exhaustive robustness analysis as well as adding specific criteria to explicitly ensure robustness during the control synthesis are let for further work.

2.2 The ${{\varvec{H}}_\infty }$ optimal control with preview

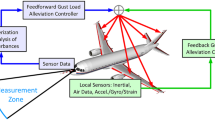
In the present paper, it is assumed (with no further discussion) that a sensor system is able to perfectly measure the vertical wind at some distance ahead of the aircraft, and therefore, the vertical wind over a small time horizon in the future is known. The interested reader is referred to [15, 16] and the references therein for further information on the sensor technologies that could provide this capability.

In practice, the sensor measures the wind vector at the current time, but at a location that the aircraft has not reached yet. Even if, in the considered configuration, the wind measurement is not expected to change significantly during the time the aircraft needs to reach the measurement location, it could theoretically change; and hence, the correct physical interpretation is that it is a remote measurement, and not a glimpse into the future. Based on the remote wind information gathered ahead of the aircraft at the present time and in the past, and based on the aircraft motion, a “best guess” on the future encountered wind/turbulence is made, and then used to anticipate and alleviate the resulting structural loads.

Preview control is a term that is found in the literature, see, e.g., [8, 17,18,19,20] and references therein, and which appears to be the most helpful search keyword for finding control design techniques for problems in which some reference or disturbance is “totally or partly known in advance”. This very wide and inclusive definition of the term preview control is the one used here by the authors. Note that this simple definition is fully problem-oriented, and not technique/algorithm-oriented at all. Note also that some applications of the so-called “model predictive control” (MPC) techniques are captured by this definition.

In the work presented in [3], the authors formulated the preview load alleviation problem as an ${H_\infty }$ optimal control with preview problem. This formulation leads to the exact same problem structure as in various previous works on preview control, e.g., [8]. A discrete-time state-space representation is preferred here due to the fact that it eases significantly the expression of the time delay involved in the preview.

To synthesize a controller based on the formulation of discrete-time $H_\infty$ optimal control with preview, the hands-on procedure given below is proposed:

• 1. Obtaining the bare linear model of the aircraft and adjusting it to be in the standard form for $H_\infty$ control:

  • (a) Trim the nonlinear model at the desired operating point.

  • (b) Linearize the model at the trim point from the previous step.

  • (c) Include the actuator/sensor dynamics—if not already included in the original nonlinear model.

  • (d) Add the exogenous disturbance inputs (without delay) to the linear model—if not already added to the original nonlinear model.

• 2. Normalizing and weighting the performance channels:

  • (a) Normalize the inputs and outputs of the performance channels to obtain an open-loop $H_\infty$ norm $\cong 1$.

  • (b) Add the appropriate input- and control-action weighting functions.

• 3. Obtaining the discrete-time preview system model:

  • (a) Discretize the model with an adequate sampling time.

  • (b) Add a chain of h unit delays to obtain the discrete-time preview system model.

  • (c) Augment the measurement vector to include the previewed signal.

• 4. Proceeding to the steps that a specific control design method may require (e.g., MATLAB’s hinfsyn or hinfstruct functions).

The addition of delays for the preview input, see step 4.b., is detailed in Fig. 2. The discrete-time plant, G(z), contains the model of the system, with its performance channels from w to z, the control input u, and the “regular” measurements y. It also contains an input d that is a signal which can be previewed over a number of h steps (for the chosen sampling time). The letter d was chosen here as we are considering the preview of a disturbance (vertical wind); however, the future evolution of a reference input might also be known slightly in advance (e.g., guidance commands passed to an inner-loop controller). $d_p$ represents the measurement that is being taken at the current time, and that (if perfectly measured and not changed in between) will become d after h time steps.

Fig. 2

Augmentation of the discrete-time $H_\infty$ control design plant taking the previewed disturbance into account

Unlike in many other works with preview control, the formulation of Fig. 2 includes an explicit buffering of the previewed input, such that the whole previewed input, as well as its h previous values, are explicitly passed to the controller. Theoretically, the controller states could be used to implement a similar buffering strategy, and the control design algorithms would likely tend to provide such solutions, but with the risk of having this buffer functionality mixed with other dynamic elements in a controller state-space realization that would then become scarcely interpretable. Instead, the authors prefer a solution with this explicit and imposed buffering (as shown in Fig. 2), and the controller K(z) to be as simple as possible and of low order.

Finally and depending on the exact use case, having separate preview inputs $d_p$ and performance channel input w might not be necessary. For instance, in a pure disturbance rejection scheme, the disturbance $d_p$ will also be the input of the performance channel: the connection between w and G(z) would then be removed, and the performance channel is the transfer function from $d_p$ to z. In another context, or in a multi-channel scheme, w could be another interesting physical input, e.g., another type of disturbance which can neither be measured nor be previewed, but which should also be rejected by the closed loop. Similarly, various signals could be previewed, and each could have a different preview horizon. As a consequence, Fig. 2 should be understood as a generic sketch of the different ways the original plant can be augmented for including preview signals, rather than as the only augmentation considered hereafter. Later on, the system and control design criteria used are detailed along with a flexible aircraft model.

2.3 Multi-channel $\varvec{H_\infty }$ control design

The $H_\infty$ problem described in the previous subsections only included one performance channel from $\varvec{w}$ to $\varvec{z}$. When working on multi-input multi-output (MIMO) systems, or with various (usually conflicting) control design requirements, the “mono-channel” formulation forces the designer to group the various degrees of freedom and criteria into one single transfer function, with more inputs and outputs. In most cases, this approach has very significant drawbacks: The physical interpretation of the $H_\infty$ norm of this transfer function becomes less direct or even impossible. Besides, cross terms—which are usually uninteresting or even undesirable from a control design perspective—are introduced in the overall “cost function”. For instance, in a problem where two single-input single-output (SISO) transfer functions (from $\varvec{w_1}$ to $\varvec{z_1}$ and from $\varvec{w_2}$ to $\varvec{z_2}$) are used to specify the desired behavior, the transfer functions from $\varvec{w_1}$ to $\varvec{z_2}$ and from $\varvec{w_2}$ to $\varvec{z_1}$ will necessarily be taken into account, and steer the algorithm towards suboptimal or even undesirable solutions. The “classical” and mathematically efficient algorithms for solving $H_\infty$ control design problems (e.g., [5]) are restricted to the mono-channel formulation, and additionally synthesize full-order controllers (i.e., controllers with as many states as the plant).

To overcome these restrictions, many researchers have been investigating other approaches, with the aim of permitting the synthesis of reduced-order controllers (less than the plant and possibly down to zero states) and with several independent performance channels. This currently remains a difficult problem to solve, but some algorithms exist and were integrated starting in 2011 in MATLAB’s Robust Control Toolbox (in the hinfstruct function), which made them easily available. These algorithms are based on the work presented in [6, 7] and various other papers from the same authors. The suggested approach relies on non-smooth optimization techniques, and a new multi-channel form is used, as illustrated in Fig. 3 in case of two channels. The gain $\beta$ added to the first channel can be ignored here: it only plays a role later on for the considered application.

Fig. 3

Standard form for multi-channel control synthesis

This formulation has the advantage of being very flexible: each $H_\infty$ channel is formulated based on a separate plant $P_i$, and the controller $K_i$ that must be designed can be fully independently specified (order, measurements, control commands). In practice, the plants $P_i$ are often somehow related, and the controllers $K_i$ too, but the control designer can freely select what they would like to express (no additional restrictions in the method). Regardless of the choice of the control designers regarding the plants $P_i$ and the constraints possibly imposed on the controllers $K_i$, the multi-channel control synthesis technique optimizes a program of the form given by Eq. (1), where $T_{w_i\rightarrow z_i}=F_l(P_i,K_i)$ is the closed-loop transfer function obtained by the lower linear fractional transformation of plant $P_i$ and controller $K_i$:

$$ \begin{array}{ll} {{\text{minimize }}\quad \max _{i} \left\{ {\left\| {T_{{w_{i} \to z_{i} }} = F_{l} (P_{i} ,K_{i} )} \right\|_{\infty } } \right\}} \\ {{\text{subject to}}\quad \forall i,K_{i} {\text{ stabilizes }}P_{i} } \\ \end{array} $$

(1)

This flexible formulation can for instance be used to make a trade-off between various $H_\infty$ requirements by selecting various different transfer functions for the same model. In this case, the different plants ($P_1$, $P_2$, etc.) are basically representing the same bare dynamic system, but with different performance channel input vectors $w_i$ and output vectors $z_i$. Note that, in that case, the plants might contain states that are needed for some weighting functions, in addition to the states of the bare system. When the same bare system is considered with different performance channels, additional constraints are set for the controllers $K_i$ to ensure that they are equal: we are then looking for one unique controller that satisfies all the $H_\infty$-criteria. This flexible formulation can also be used to perform robust control design by simultaneously considering several models (e.g., corresponding to various operating points or with different values for some uncertain parameters). This possibility is not used in the present work, but is used in other works of the authors.

In the following, the same basic model is used with different performance output vectors, but with the same control input vectors ($u_1=u_2=\cdots$) and measurement vectors ($y_1=y_2=\cdots$). This multi-channel control synthesis problem can also be represented by the interconnection of Fig. 4. The designers can express their preferences in terms of trade-off between the channels by carefully selecting and introducing static/dynamic weighting functions on the inputs $w_i$ and outputs $z_i$ of the performance channels. Note that the inputs $w_i$ and outputs $z_i$ can be vectors, and the transfer function $T_{w_i\rightarrow z_i}$ will have possibly several singular values. The obvious advantage of this multi-channel formulation, compared to considering the transfer $T_{[w_1, w_2, \ldots ]^T\rightarrow [z_1, z_2, \ldots ]^T}$ obtained by merging all performance channels, is that the cross transfer functions $T_{w_i\rightarrow z_j}$, with ($i\ne j$), are not part of the cost function to be minimized. In most control design problems, these cross transfer functions make no sense for the control design problem.

Fig. 4

Multi-channel single model and single controller control synthesis

2.4 Converting performance target values to weighting gains

Most control design tasks involve some trade-off between conflicting objectives and constraints. The control designers should understand the real constraints and needs of their application as well as the corresponding priorities between them. Eventually, they should translate them into well-defined mathematical objective or constraint functions, which can be provided to the control design algorithms. For the design of load alleviation function, the real objective is to enable a reduction of the overall structural weight of the airplane. To enable this weight reduction, the loads envelope—defined through the minimum and maximum loads occurring in all cases specified in the certification—must be reduced. Static and dynamic loads result from a large number of situations: gusts, maneuvers, landing, high-speed taxiing, pressurization, gyroscopic effects, etc. Consequently, a gust load alleviation function can lead to weight reduction only when the sizing cases result from gust loads. If the second highest loads are, for example, 10% lower than the gust loads without load alleviation function, then gust load reductions up to 10% correlate with potential weight savings. Beyond this value, weight savings can only be obtained if these second highest loads are also reduced. In addition, it is very often that gust load reductions at some locations (e.g., at wing root) will be obtained at the expense of gust load increase at some other locations (e.g., near the control surfaces used by the load alleviation function). Hence, a trade-off between the weight savings and penalties over the complete aircraft has to be made. Defining the performance target values for each load station is a complex task, and in practice, this requires not only the knowledge of a complete loads hierarchy (i.e., a ranking of all load cases for every load station), but also of the manufacturing constraints (e.g., minimum sheet thickness). The definition of the target values for the load alleviation performance is outside the scope of this paper, and is considered as part of the requirements and design objectives that the designer of the load alleviation function receives from the structure and overall design groups. The question that we are concerned about here is how to translate those requirements/objectives, whichever values they take, into a form that the $H_\infty$ control design algorithm can handle.

To ease the expression of the design preferences, the various loads are usually normalized first. This is necessary due to the fact that the orders of magnitude for the considered loads strongly differ (e.g., between wing root bending moments and the bending moment at the most outboard locations). The signals usually are not even of the same physical dimension (e.g., bending moment vs. shear force). A typical way of normalizing these loads is to divide them by their corresponding load envelope values. This results in normalized loads with values above one for load increases and values below one for load reductions.

After this normalization step, if all loads are to be reduced to 0.9 or less of their original values, then at least 10% load reduction will be gained. Preferences between these loads are expressed by multiplying them by additional factors. By multiplying, for example, a particular load channel by a factor of 1/0.85 and an another by a factor of 1/1.05, the designer can express that a reduction of 15% is desired on the former load channel ($0.85 = 1 -$ 15%), and that to reach this performance, an increase of 5% can be tolerated on the latter ($1.05 = 1 +$ 5%). The control design algorithm will be configured, such that a target performance of 1 is sought. If the algorithm could theoretically reach a better performance, it should not, however, be achieved. The underlying idea of this is that a controller which achieves a better performance than required will (in most cases) have a higher control activity. This is undesired, because it increases the actuator load cycles, potentially increases the structural fatigue near the control surface, and might reduce the robustness margins, especially against unmodeled dynamics or delays. The desired load reduction or tolerable load increase for each channel is a tuning parameter for the load alleviation function designer.

There are often additional performance margins that need to be considered. Indeed, some effects might not be possible or easy to be taken into account, such as uncertainties in the control design problem. These are, for instance, the errors in the gust and turbulence fields determined by a Doppler LIDAR sensor. Instead of attempting to take these errors (and their complex inter-dependencies) explicitly into account, the synthesis is performed under the assumption that the previewed wind information is perfect, but with an additional margin defined on the load alleviation performance requirements. For instance, if a 10% alleviation performance is desired, then the control design will be made with a target of “10% + margin” (say 14%), and a perfect wind information will be assumed. The margin needs to be defined, such that in practice, the load alleviation performance obtained still reaches the desired 10% when having the imperfect wind information. Due to the complexity of the wind reconstruction errors, it might become necessary to determine the level of performance margin to be applied in an iterative way.

3 Application to gust load alleviation with preview

3.1 Used flexible aircraft model

3.1.1 DLR’s Discus-2c sailplane

Although this work is primarily intended to be applied to large transport aircraft (CS/Part 25 of the airworthiness standards), an aeroelastic model of a sailplane (DLR’s Discus-2c, shown in Fig. 5) is used hereafter. The sailplane model used hereafter was chosen, because it is readily available to both authors and is suited for gust load alleviation purposes. The model and the loads sensor calibration were derived from flight tests using system identification, and exhibited excellent match with the test data. The orders of magnitude in terms of loads and velocity are very different from the ones of a large transport aircraft, but the model structure as well as the relationships and coupling between states, inputs, and outputs are representative of those of a large transport aircraft.

Fig. 5

DLR’s Discus-2c sailplane in flight

The DLR’s Discus-2c is a high-performance single-seat sailplane. The aircraft has the general mass and geometry characteristics given in Table 1. The aircraft is equipped with a flight test instrumentation which includes: a 5-hole probe nose boom, a GPS receiver, an INS platform, 46 strain gauge sensors, and 15 three-axis accelerometers at different aircraft locations. Previous flight test campaigns provided the data, and enabled the development of a nonlinear aeroelastic model of the aircraft using system identification techniques (see [21, 22] and the references therein). The structure of this aeroelastic model is presented in Sect. 3.1.2. The aeroelastic model allows for the calculation of the shear forces and torsional and bending moments at 7 different load stations: 6 per wing (WR1 / WR4 / WR6 / WL1 / WL4 / WL6), and 1 for the horizontal tail (HTR), as shown in Fig. 6.

Table 1 DLR’s Discus-2c geometry and mass characteristics

Fig. 6

DLR’s Discus-2c load stations and distribution of measurement sensors (red circles: accelerometers)

In this work, only the symmetric motion and loads are considered; hence, only 3 load stations (WR1/WR4/WR6) and 5 accelerometers (WR4F/WR4R/WR7F/WR8F/WR8R) of the right wing semi-span, plus 1 accelerometer of the IMU (for ride qualities), will be considered, see Fig. 6. The horizontal tail loads and accelerometers will not be considered. For the rigid-body motion, only the short-period mode is considered (the phugoid mode has a very low frequency compared to either the short period mode or the structural modes, and almost is not excited during the gust encounter). For the flexible degrees of freedom, out of the three symmetric structural modes that were included in the nonlinear aeroelastic model, only the first and second wing vertical bending modes (see Table 2) are considered (The third mode which represents the wing in-plane bending is almost not excited at all during such vertical gust encounter, and hence is not included here). Since only symmetrical gusts and turbulence are considered hereafter, only the following two control surfaces were kept in the model: the elevator on the horizontal tail with first-order actuator dynamics, and the symmetric ailerons on the wing with another first-order actuator dynamics. The ailerons of the real sailplane are mechanically connected and can only be deflected asymmetrically: the symmetrical aileron deflection capability only exists virtually in the simulation model. The model used in this work has 10 regulated output channels: 1 for normal load factor at pilot location ($n_z^\mathrm{pilot}$, non-dimensional), 3 for shear force (SR1/SR4/SR6, in newtons), 3 for torsional moment (TR1/TR4/TR6, in newton-meters), and 3 for bending moment (BR1/BR4/BR6, in newton-meters).

Table 2 DLR’s Discus-2c modal characteristics (in vacuum)

3.1.2 Model equations

The general equations of motion of a rigid aircraft can be expressed in the body axis system as in Eq. (2), whereas Eq. (3) represents the rigid-body kinematics equations, and finally, the rate of change of the center of gravity (CG) position measured with respect to the inertial axis system is given by Eq. (4), see [23, 24]. Here, $u_K$, $v_K$, and $w_K$ are the components of the velocity vector of the CG relative to the inertial (Newtonian) axis system (i.e., ground speed), p, q, and r are the rotational velocities in body axes, $\varPhi$, $\varTheta$ and $\varPsi$ are the 3-2-1 Euler angles, x, y, and z are the components of the position vector, X, Y, and Z are the total external (aerodynamic + propulsive) forces, L, M, and N are the total external (aerodynamic + propulsive) moments, m is the aircraft mass, g is the gravitational acceleration, and finally, $I_{..}$ are the aircraft moments and products of inertia around different axes (with “.” being x, y, or z). In Eq. (5), the relation between (u, v, and w), ($u_K$, $v_K$, and $w_K$) and ($u_W$, $v_W$, and $w_W$) is given, where u, v, and w are the components of the velocity vector of the CG relative to the air (i.e., airspeed), whereas $u_W$, $v_W$, and $w_W$ are the components of the wind velocity vector relative to the inertial axis system:

$$\begin{aligned}&m\left( \dot{u}_K+qw_K-rv_K\right) +mg\sin {\varTheta }=\text {X} \nonumber \\&m\left( \dot{v}_K+ru_K-pw_K\right) -mg\cos {\varTheta }\sin {\varPhi }=Y \nonumber \\&m\left( \dot{w}_K+pv_K-qu_K\right) -mg\cos {\varTheta }\cos {\varPhi }=Z \nonumber \\&I_{xx}\dot{p}-I_{xy}\left( \dot{q}-pr\right) -I_{xz}\left( \dot{r}+pq\right) \nonumber \\&\quad -I_{yz}\left( q^2-r^2\right) +\left( I_{zz}-I_{yy}\right) qr=L \nonumber \\&I_{yy}\dot{q}-I_{xy}\left( \dot{p}+qr\right) -I_{yz}\left( \dot{r}-pq\right) \nonumber \\&\quad +I_{xz}\left( p^2-r^2\right) +\left( I_{xx}-I_{zz}\right) pr=M \nonumber \\&I_{zz}\dot{r}-I_{xz}\left( \dot{p}-qr\right) -I_{yz}\left( \dot{q}+pr\right) \nonumber \\&\quad -I_{xy}\left( p^2-q^2\right) +\left( I_{yy}-I_{xx}\right) pq=N \end{aligned}$$

(2)

$$\begin{aligned}&\dot{\varPhi }=p+q\left( \sin {\varPhi }\tan {\varTheta }\right) +r\left( \cos {\varPhi }\tan {\varTheta }\right) \nonumber \\&\dot{\varTheta }=q\cos {\varPhi }-r\sin {\varPhi } \nonumber \\&\dot{\varPsi }=q\left( \sin {\varPhi }\sec {\varTheta }\right) +r\left( \cos {\varPhi }\sec {\varTheta }\right) \end{aligned}$$

(3)

$$\begin{aligned}&\left[ \begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{z} \end{array} \right] = \left[ \begin{array}{ccc} \cos {\varPsi } &{} -\sin {\varPsi } &{} 0 \\ \sin {\varPsi } &{} \cos {\varPsi } &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] \nonumber \\&\quad \left[ \begin{array}{ccc} \cos {\varTheta } &{} 0 &{} \sin {\varTheta } \\ 0 &{} 1 &{} 0 \\ -\sin {\varTheta } &{} 0 &{} \cos {\varTheta } \end{array} \right] \left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} \cos {\varPhi } &{} -\sin {\varPhi } \\ 0 &{} \sin {\varPhi } &{} \cos {\varPhi } \end{array} \right] \left[ \begin{array}{c} {u}_K \\ {v}_K \\ {w}_K \end{array} \right] \end{aligned}$$

(4)

$$\begin{aligned}&u=u_K-u_W \nonumber \\&v=v_K-v_W \nonumber \\&w=w_K-w_W. \end{aligned}$$

(5)

Using the concept of a lumped-mass vibration structure, the total elastic displacement of that structure might be expressed in the structural reference axis system in terms of modal expansion using n free-vibration modes as in Eq. (6), where $d_E$ is the total elastic deformation, $\phi _i$ is the vibration mode shape (eigenfunction), and $\eta _i$ is the generalized coordinate associated with the ith vibration mode:

$$\begin{aligned} d_E\left( x,y,z,t\right) =\sum _{i=1}^n {\phi _i\left( x,y,z\right) \eta _i\left( t\right) }. \end{aligned}$$

(6)

These n generalized coordinates are governed by the n equations given by Eq. (7), where $\zeta _i$ and $\omega _i$ are the modal damping and natural frequency, respectively, whereas $m_i$ and $Q_i$ are the generalized mass and force, respectively, each associated with the $i^{th}$ vibration mode:

$$\begin{aligned} \ddot{\eta }_i+2\zeta _i\omega _i\dot{\eta }_i+\omega _i^2\eta _i=\frac{Q_i}{m_i}, \quad i=1,2,\ldots , n. \end{aligned}$$

(7)

Using the mean axis system (one at which the relative translational and angular momenta about the center of mass resulting from elastic deformation of a structure undergoing free vibration diminish at every instant, see [24]), the aeroelastic model is constituted of Eqs. (2), (3), (4), and (7). These equations are $12+n$ in number, have $12+2n$ states, and are nonlinear and coupled differential equations of first and second order.

To complete the aeroelastic model, expressions for the external forces and moments and the generalized forces are needed (i.e., aerodynamic model). The aerodynamic model used in this work is expressed via partial derivatives (aerodynamic transfer functions) of the motion variables, control surface inputs, and the flexible degrees of freedom of the aircraft. For the example aircraft used for the simulation in this work, these derivatives had been obtained by system identification from flight tests (see [21, 22]). For a more detailed description of the aeroelastic model, interested readers may refer to [25], which is a paper by the first author of this work. These $12+n$ nonlinear differential equations can then be solved for trim at a given steady flight condition. After solving the trim problem, they can be dissolved into steady equations, plus small perturbations (linear differential equations) added to them. The resulting linear differential equations (in state-space form) will then be used for the control synthesis as will be seen in the next sections. For all the results presented hereafter, the chosen steady flight condition is defined by a steady rectilinear flight (cruise) with a true airspeed $V_\mathrm{TAS} = 160$ km/h, and an altitude $H = 3000$ m (with standard atmospheric conditions).

3.2 Control design problem

In this application, two $H_\infty$ performance channels were defined. For both channels, the vertical wind is the only input. The output of the first performance channel is the variation of the vertical load factor at the pilot’s location. The output of the second performance channel is the vector of the nine normalized load variations: $\varDelta$BR1, $\varDelta$SR1, $\varDelta$TR1, $\varDelta$BR4, $\varDelta$SR4, $\varDelta$TR4, $\varDelta$BR6, $\varDelta$SR6, and $\varDelta$TR6. In addition to the previewed disturbance measurement, the IMU measurements as well as the measurements from several accelerometers on the structure are considered.

To illustrate the trade-off that can be made between the vertical load factor at the pilot’s location (which can be understood as a passenger comfort criterion; first channel) and the structural loads (second channel), a weighting factor $\beta$ is introduced on the vertical load factor channel (see Fig. 3). Increasing $\beta$ increases the importance given to the passenger comfort compared to the structural loads.

The results shown hereafter are based on two different formulations. The first one is based on a single-channel formulation, with the two aforementioned channels merged into one single channel (with $\beta = 1$), and solved with both the full-order technique (using MATLAB’s hinfsyn function) and the fixed-structure technique (using MATLAB’s hinfstruct function). This formulation permits to compare both techniques on a common example. The second formulation is the actual multi-channel formulation as described earlier, and which can only be solved with the latter technique.

The model used (see Sect. 3.1) is already of fairly low order. It contained 12 states for the rigid-body part and $2 \times 6$ states for the 6 flexible modes available. Once restricted to the relevant modes (short period and two wing vertical bending modes), it was only of order 6. As a consequence, no model reduction step is required for this model. However, building precise aeroelastic models for industrial configurations is a complicated task, which has become an entire discipline [26]. Simplified aeroelastic models are usually provided to the control designers, but are still typically between a few hundred to a few thousand states. These models are suited for load evaluations with load alleviations functions, but not suited for control design. In such cases, a model reduction step is required before being able to proceed to the control synthesis [27, 28].

Finally, when using full-order $H_\infty$ techniques, controllers having the same number of states as the control design problem are obtained. These controllers might be exhibiting very fast modes, and be unsuited for implementation on the flight control computer. This requires reducing the order of the controller after the synthesis. The controller reduction step is usually significantly more difficult than the model reduction [29]. Fortunately, this step can be avoided using the fixed-structure $H_\infty$ techniques, which permit to directly synthesize reduced-order controllers.

3.3 Results

First, the results provided by both techniques for the single-channel problem are compared. In the case of full-order discrete-time $H_\infty$ optimal control, it can be seen from Fig. 7 that the $H_\infty$ norm decreases from 1.07 for the feedback-only case to 0.96 when a zero-preview feedforward loop is added. After that, it decreases monotonically with increasing preview length (or preview time), until reaching a lowest value of 0.68 at a preview length of 18 (or a preview time of 0.18 s with the sampling time of 10 ms used). After reaching this lowest value, no more performance enhancement could be obtained even with increasing the preview length.

In the case of multi-channel fixed-structure $H_\infty$ optimal control, it can be seen from Fig. 7 that the overall behavior with increasing preview horizon is very similar to the full-order case. By increasing the tuning parameter ${\beta }$, the $H_\infty$ norm of the overall system increases, which, for the first impression, might be seen as a performance degradation; it is not, as will be explained shortly after.

Fig. 7

${H_\infty }$ norm as function of preview length for different values of tuning parameter (FB: Feedback-only)

The multi-channel synthesis actually minimizes the maximum of both channels taken separately. The $H_\infty$ norm of each channel (without the additional weight $\beta$ on the first channel) is shown separately in Fig. 8. It can be seen that the $H_\infty$ norm of the normal load factor at pilot location (channel 1) decreases with increasing the tuning parameter ${\beta }$ (i.e., a performance enhancement for this specific channel). On the other hand, this comes at the expense of increasing the $H_\infty$ norm of the structural loads (channel 2). This behavior was expected and typical for a change in relative weighting between objectives in multi-objective optimization. The evolution of the first channel norm with increasing preview length h is not monotonically decreasing in the case $\beta =2$. The first channel in the case $h=0$ (vertical wind available instantaneously but not in advance) has a higher $H_\infty$ norm than in the feedback case (no wind measurement at all). The reason for that is that in both of these cases, the $H_\infty$ norms of the first channel—once multiplied with $\beta =2$—are still lower than the $H_\infty$ norms of the second channel. The control design algorithm therefore fully used the additional wind information to improve the most critical criteria: the loads, i.e., the performance of the second channel.

Fig. 8

${H_\infty }$ norm of each channel as function of preview length for different values of tuning parameter (FB: feedback-only, Channel 1: normal load factor at pilot location, Channel 2: structural loads)

The previous results can be confirmed by looking at the peak values obtained from time-domain simulations of the system. To do so, for each controller, a gust encounter was simulated, and the maximum absolute values (over time) of the various loads, of the load factor at pilot’s location, and of the control surface deflections, are calculated and shown in Fig. 9. In this figure, each subplot represents the peak values of a regulated output as vertical bars. As in the previous figures, the colors represent different relative weighting between the performance channels. Along the x-axis, various controller configurations, from a pure feedback controller to controllers with increasing preview length h, are represented. The trade-off between the first performance channel (load factor at pilot location) and the second channel (structural loads) can be seen in the change in length of the bars with different colors.

It can be seen from Fig. 9 that improving the response of the system on the load factor leads to a reduction of the load alleviation performance for the main loads stations (e.g., BR1, BR4, SR1), and vice versa. Including the wind measurement (low values for h compared to the pure feedback case) leads to increased maximum control surface deflections at first. The further increase of the preview horizon (i.e., increasing h) leads to loads and load factor improvements, without requiring higher control surface deflections, which is very advantageous. The general trend for the maximum control surface deflections is not very obvious, but seems to indicate a decrease in control surface deflections with increasing the preview horizon.

The overall behavior of the achievable load alleviation performance with the increasing the preview length confirms the trends observed already in [3] with a single performance channel and fewer load stations. On the load stations WR4 and WR6, the bending and torsional moments are improve drastically, with fairly small preview length. The evolution of the shear forces at stations WR4 and WR6 is different. A large improvement is obtained in case of feedback-only control, compared to the open-loop system. After that, the shear forces get traded for significant improvements on the other load stations until a preview length of 6–9. With further increase of the preview length $h>9$, the peak loads of the shear forces progressively decrease again, while the bending and torsional moments remain constant.

In summary, including the preview measurements from the LIDAR sensor leads to much better load alleviation performance, compared to either the open-loop system or the feedback-only control. This enhancement in performance is seen in: first, lower load factor at pilot location, and hence higher passengers comfort; second, lower structural loads, and hence possible structural weight reduction; and third, reasonable control activity.

4 Conclusion

A new formulation of the control design of combined feedforward and feedback load alleviation functions, based on a combination of discrete-time multi-channel $H_\infty$ control techniques and preview control, was presented. This work complements a series of previous works published by the authors as well as other researchers. The application to a sailplane model showed that this control design methodology is very promising for load alleviation function design. As a consequence, this methodology is now being integrated into the control design tools developed by the authors and their colleagues, which permits designing and analyzing active load alleviation function for industry-size problems, with hundreds to thousands of states and as many load stations.

Fig. 9

Maximum absolute values of the control inputs and the regulated outputs as function of preview length for different values of tuning parameter (OL: open loop, FB: feedback-only, black: full-order, green: fixed-structure ${\beta }=2$, cyan: fixed-structure ${\beta }=4$, gray: fixed-structure ${\beta }=6$)