Stage-Structured Transmission Model Incorporating Secondary Dengue Infection

Abstract

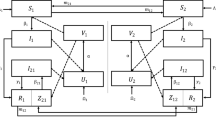
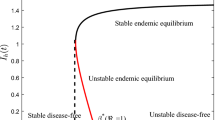
In this paper, a non-linear stage-structured model has been formulated to study the effects of primary/secondary dengue infection on children and adults. It is assumed that a proportion of susceptible children have been previously infected by a serotype asymptomatically. After recovery from asymptomatic infection, the immunity is developed for the particular serotype but they remain susceptible to heterologous serotypes. These children may get secondary infection when exposed to a different serotype. The model has two equilibrium states. Global/local stability of equilibrium states have been discussed. The stability of disease-free state changes at $R_0=1$. Applying the center manifold theory, the existence of forward bifurcation is possible. This concludes that the primary/secondary infection in children as well as in adults population could be eradicated for $R_0<1$. Numerical results are used to explore the global behavior of disease-free/endemic state for choice of arbitrary initial conditions.

Appendix

Center Manifold Analysis at $R_0=1$

consider a general system of ODEs with parameter $\phi$:

$$\begin{aligned} \dfrac{dx}{dt}=f(x,\phi ), \quad \hbox {f}: \mathbb {R}^n \times \mathbb {R} \rightarrow \mathbb {R}^n \quad \hbox { and } \quad f\in C^2(\mathbb {R}^n \times \mathbb {R}) \end{aligned}$$

(21)

Without loss of generality, it is assumed that $x^*$ is the disease-free point for system (21) for all values of the parameter $\phi$.i.e.

$$\begin{aligned} f(x^*,\phi )\equiv 0 \quad \forall \; \phi \end{aligned}$$

Lemma 2

[29] Assume:

• (A1) $Q=D_xf(x^*,\phi ^*)$ is the linearization matrix of system (21) about the equilibrium $x^*$ with $\phi$ evaluated at $\phi ^*$. Zero is a simple eigenvalue of Q and all other eigenvalues of Q have negative real parts;

• (A2) Matrix Q has a non-negative right eigenvector $\omega$ and a left eigenvector $\nu$ corresponding to the zero eigenvalue.

Let $f_k$ denotes the kth component of f and

$$\begin{aligned} \mathbf{a}= & {} \mathop \sum \nolimits _{i,j,k=1}^n\nu _k\omega _i\omega _j\dfrac{\partial ^2f_k}{\partial x_i x_j}(x^*,\phi ^*), \\ \mathbf{b}= & {} \mathop \sum \nolimits _{i,j,k=1}^n\nu _k\omega _i\dfrac{\partial ^2f_k}{\partial x_i \phi }(x^*,\phi ^*), \\ \end{aligned}$$

Then the local dynamics of system (20) around the state $x^*$ are totally determined by $\mathbf{a}$ and $\mathbf{b}$.

• 1. $\mathbf{a}> 0, \mathbf{b}> 0$. When $\phi < \phi ^*$ with $|\phi -\phi ^*|\ll 1, x^*$ is locally asymptotically stable and there exists a positive unstable equilibrium. When $\phi >\phi ^*$ with $|\phi -\phi ^*|\ll 1, x^*$ is unstable and there exists a negative and locally asymptotically stable equilibrium.

• 2. $\mathbf{a}< 0, \mathbf{b}< 0$. When $\phi <\phi ^*$ with $|\phi -\phi ^*|\ll 1, x^*$ is unstable. When $\phi >\phi ^*$ with $|\phi -\phi ^*|\ll 1, x^*$ is locally asymptotically stable and there exists a positive unstable equilibrium.

• 3. $\mathbf{a}>0, \mathbf{b}< 0$. When $\phi < \phi ^*$ with $|\phi -\phi ^*|\ll 1, x^*$ is unstable and there exists a locally asymptotically stable negative equilibrium. When $\phi >\phi ^*$ with $|\phi -\phi ^*|\ll 1, x^*$ is stable and a positive unstable equilibrium appears.

• 4. $\mathbf{a}< 0, \mathbf{b}> 0$. When $\phi -\phi ^*$ changes from negative to positive, $x^*$ changes its stability from stable to unstable. Correspondingly, a negative unstable endemic equilibrium becomes positive and locally asymptotically stable.

Considering $\beta _1$ to be the bifurcation parameter, $\beta _1=\beta _1^{c}$ corresponds to $R_0=1$:

$$\begin{aligned} \beta _1^{c}=\dfrac{\gamma _1+\mu }{\rho }\left( \dfrac{\mu _1^2(\alpha _1+\mu )}{\sigma \omega \omega _1}-\dfrac{\beta \alpha _1}{\mu (\gamma +\mu )}\right) \end{aligned}$$

The further analysis is as follows: Let $\mathbf{{\delta }}=(\delta _1, \delta _2, \delta _3, \delta _4, \delta _5, \delta _6)^{T}$ be a right eigenvector associated with the zero eigenvalue. It is given by

$$\begin{aligned}&\left( {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} -\alpha _1-\mu &{} 0 &{} 0 &{} 0 &{} 0 &{}-(\beta _1^c\rho +\beta _2(1-\rho ))\hat{S} \\ 0 &{} -\gamma _1-\mu &{} 0 &{} 0 &{} 0 &{} \beta _1^c\rho \hat{S} \\ 0 &{} 0 &{} -(\gamma _2+\mu +e) &{} 0 &{} 0 &{} \beta _2(1-\rho )\hat{S} \\ \alpha _1 &{} 0 &{} 0 &{} -\mu &{} 0 &{} -\beta \hat{A}\\ 0 &{} 0 &{} 0 &{} 0 &{} -\gamma -\mu &{} \beta \hat{A}\\ 0 &{} \dfrac{\sigma \omega _1}{\mu _1} &{} 0 &{} 0 &{} \dfrac{\omega _1\sigma }{\mu _1} &{} -\mu _1\\ \end{array}} \right) \\&\quad \times \;\left( {\begin{array}{c} \delta _1 \\ \delta _2\\ \delta _3\\ \delta _4\\ \delta _5\\ \delta _6 \end{array}} \right) =0\\ \end{aligned}$$

or, the above system can be written as;

$$\begin{aligned}&(\alpha _1+\mu ) \delta _1 +(\beta _1^c\rho +\beta _2(1-\rho ))\hat{S}=0\\&-(\gamma _1+\mu )\delta _2+\beta _1^c\rho \hat{S} \delta _6=0\\&-(\gamma _2+\mu +d)\delta _3+\beta _2(1-\rho )\hat{S}\delta _6=0\\&\alpha _1 \delta _1-\mu \delta _4-\beta \hat{A}\delta _6=0\\&-(\gamma +\mu )\delta _5+ \beta \hat{A}\delta _6=0\\&\dfrac{\sigma \omega _1}{\mu _1}\delta _2+\dfrac{\omega _1\sigma }{\mu _1}\delta _5-\mu _1\delta _6=0 \end{aligned}$$

Solving above equations, the right eigenvector is given as

$$\begin{aligned} \varvec{\delta }=\left( \delta _1=0, \quad \delta _2=\dfrac{\beta _1^c\rho }{(\gamma _1+\mu )}, \quad \delta _3=0, \quad \delta _4=0, \quad \delta _5=\dfrac{\beta \alpha _1}{\mu (\gamma _1+\mu )}, \quad \delta _6=\dfrac{(\alpha _1+\mu )(\gamma +\mu )}{\omega (\gamma _1+\mu )}\right) \\ \end{aligned}$$

Further, the left eigenvector $\nu =(\nu _1, \nu _2, \nu _3, \nu _4, \nu _5, \nu _6)^{T}$ associated with the zero eigenvalue such that $\delta \cdot \nu =1$ is given as

$$\begin{aligned}&-(\alpha _1+\mu ) \nu _1 +\alpha _1\nu _4=0\\&-(\gamma _1+\mu )\nu _2+\sigma \dfrac{\omega _1}{\mu _1}\nu _6=0\\&-(\gamma _2+\mu +d)\nu _3=0\\&-\mu \nu _4=0\\&-(\gamma +\mu )\nu _5+ \sigma \dfrac{\omega _1}{\mu _1}\nu _6=0\\&-\beta \hat{S}\nu _1+ \beta _1^c\rho \hat{S}\nu _2+\beta _2(1-\rho )\hat{S}\nu _3-\beta \hat{A}\nu _4+\beta \hat{A}\nu _5-\mu _1\nu _6=0 \end{aligned}$$

Now, the left eigenvector is computed to be

$$\begin{aligned} \Big (\nu _1&=0, \nu _2=\dfrac{\sigma \omega _1\omega }{\mu _1(\alpha _1+\mu )(\gamma +\mu +\mu _1)}, \nu _3=0, \nu _4=0,\\ \nu _5&=\dfrac{\sigma \omega _1\omega (\gamma _1+\mu )}{\mu _1(\alpha _1+\mu )(\gamma +\mu )(\gamma +\mu +\mu _1)},\\ \nu _6&=\dfrac{\omega (\gamma _1+\mu )}{(\alpha _1+\mu )(\gamma +\mu +\mu _1)}\Big ) \end{aligned}$$

Let us introduce $S=x_1, I_1=x_2, I_2=x_3, A=x_4, I_3=x_5, V=x_6$. The system (12)–(17) becomes,

$$\begin{aligned} \frac{{d x_1 }}{{dt}}= & {} \omega - \alpha _1x_1 - \beta _1\rho x_1x_6 -\beta _2(1-\rho ) x_1x_6 - \mu x_1 :=f_1 \end{aligned}$$

(22)

$$\begin{aligned} \frac{{dx_2 }}{{dt}}= & {} \beta _1\rho x_1x_6 - \gamma _1 x_2 - \mu x_2 :=f_2 \end{aligned}$$

(23)

$$\begin{aligned} \frac{{dx_3 }}{{dt}}= & {} \beta _2(1-\rho )x_1x_6 - \gamma _2 x_3 - \mu x_3- e x_3:=f_3 \end{aligned}$$

(24)

$$\begin{aligned} \frac{{dx_4}}{{dt}}= & {} \alpha _1x_1 -\beta x_4x_6 -\mu x_4 :=f_4 \end{aligned}$$

(25)

$$\begin{aligned} \frac{{dx_5 }}{{dt}}= & {} \beta x_4x_6 - \gamma x_5 - \mu x_5:=f_5 \end{aligned}$$

(26)

$$\begin{aligned} \frac{{dx_6}}{{dt}}= & {} \sigma \left( \dfrac{\omega _1}{\mu _1}-x_6\right) (x_2+x_5) - \mu _1 x_6:=f_6 \end{aligned}$$

(27)

The non-zero partial derivatives at the disease-free state ($E_0$) are turn out to be

$$\begin{aligned} \dfrac{\partial ^2f_6}{\partial x_2 \partial x_6}= & {} \dfrac{\partial ^2f_6}{\partial x_6 \partial x_2}=-\sigma \\ \dfrac{\partial ^2f_6}{\partial x_6 \partial x_5}= & {} \dfrac{\partial ^2f_6}{\partial x_5 \partial x_6}=-\sigma \\ \dfrac{\partial ^2f_2}{\partial x_6 \partial \beta _1}= & {} \dfrac{\rho \omega }{(\alpha _1+\mu )}\\ \end{aligned}$$

The rest of the partial derivatives at $E_0$ remain zero. From Lemma 2, the coefficients $\mathbf{a}$ and $\mathbf{b}$ are computed as,

$$\begin{aligned} \mathbf{a}= & {} 2 \nu _6\delta _2\delta _6\dfrac{\partial ^2f_6}{\partial x_6 \partial x_2} +2 \nu _6\delta _5\delta _6\dfrac{\partial ^2f_6}{\partial x_6 \partial x_5}; \\ \mathbf{b}= & {} \nu _2\delta _6\dfrac{\partial ^2f_2}{\partial x_6 \partial \beta _1} \end{aligned}$$

By substituting the partial derivatives and the left and right eigenvectors from above analysis, the $\mathbf{a}$ and $\mathbf{b}$ are as follows:

$$\begin{aligned} \mathbf{a}= & {} -\dfrac{2\sigma (\gamma +\mu )}{(\gamma +\mu +\mu _1)(\gamma _1+\mu )}(\beta _1\rho +\beta \alpha _1);\\ \mathbf{b}= & {} \dfrac{\sigma \omega _1\omega \rho (\gamma +\mu )}{(\gamma _1+\mu )\mu _1(\alpha _1+\mu )(\gamma +\mu +\mu _1)} \end{aligned}$$

It is observed that $\mathbf{a}<0$ and $\mathbf{b}>0$ always. Using Lemma 2, forward bifurcation is possible only and the endemic point is found to be locally asymptotically stable for $R_0>1$.

Next Generation Matrix Method [27]

The next generation matrix is defined as the square matrix K in which the $ij^{th}$ element of $K, k_{ij}$, is the expected number of secondary infections of type i caused by a single infected individual of type j by assuming that the population of type i is completely susceptible. That is, each element of the matrix K is a reproduction number, but one where who infects whom is accounted for [27]. The spectral radius of K is the basic reproduction number. The spectral radius is the also known as the dominant eigenvalue of K. The next generation matrix has a number of desirable properties from a mathematical standpoint. In particular, it is a non-negative matrix and as such, it is guaranteed that there will be a single, unique eigenvalue which is positive, real, and strictly greater than all the others. Consider the next generation matrix K. It is comprised of two parts: F and $Y^{-1}$, where

$$\begin{aligned} F=\left[ \dfrac{\partial F_i(x_0)}{\partial x_j}\right] ; \quad Y=\left[ \dfrac{\partial Y_i(x_0)}{\partial x_j}\right] \end{aligned}$$

The $F_i$ are new infections while $Y_i$ are the transfer of infections from one compartment to another. The $x_0$ is a disease-free state. The $R_0$ is the dominant eigenvalue of the matrix $K=FV^{-1}$.