Bivariate Analysis of Birth Weight and Gestational Age by Bayesian Distributional Regression with Copulas

Abstract

We analyze perinatal data including biometric and obstetric information as well as data on maternal smoking, among others. Birth weight is the primarily interesting response variable. Gestational age is usually an important covariate and included in polynomial form. However, in opposition to this univariate regression, bivariate modeling of birth weight and gestational age is recommended to distinguish effects on each, on both, and between them. Rather than a parametric bivariate distribution, we apply conditional copula regression, where the marginal distributions of birth weight and gestational age (not necessarily of the same form) and the dependence structure are modeled conditionally on covariates. In the resulting distributional regression model, all parameters of the two marginals and the copula parameter are observation specific. While the Gaussian distribution is suitable for birth weight, the skewed gestational age data are better modeled by the three-parameter Dagum distribution. The Clayton copula performs better than the Gumbel and the symmetric Gaussian copula, indicating lower tail dependence (stronger dependence when both variables are low), although this non-linear dependence between birth weight and gestational age is surprisingly weak and only influenced by Cesarean section. A non-linear trend of birth weight on gestational age is detected by a univariate model that is polynomial with respect to the effect of gestational age. Covariate effects on the expected birth weight are similar in our copula regression model and a univariate regression model, while distributional copula regression reveals further insights, such as effects of covariates on the association between birth weight and gestational age.

1 Introduction

We analyze perinatal (newborn infants’) registry data from North Rhine-Westphalia, Germany, which contain many biometric and medical variables on mother, child, and birth. This is a part of the larger “PerSpat” (Perfluoroalkyl Spatial) project [1], concerned with the general population of North Rhine-Westphalia, which has partly been affected by environmental pollution with perfluorinated compounds [2]. There is evidence for developmental toxicity of these compounds, resulting in reduced birth weight, among other medical parameters (e.g., [3, 4]).

When analyzing perinatal data with birth weight as the response variable of primary interest, it is essential to adjust for gestational age (duration of pregnancy), which is often reported as the quantitatively most important covariate (e.g., [5,6,7]). Augmenting linear models, it may be included as a polynomial or in other parametric functional forms (e.g., [8, 9]). However, the importance of other covariates for modeling birth weight may become undetectable when gestational age predominates or mediates other influences. A widespread alternative is a binary response with a class such as “small for gestational age” (e.g., [10,11,12]), but this would mean information loss in our case.

In contrast to univariate approaches, consideration of bivariate (or multivariate) outcomes is frequent in biometric research such as meta-analysis [13], clinical trials [14], dose–response modeling [15], or with measurements from the environment [16]. Such models enable a deeper understanding of effects, when covariates’ influences on both outcomes are separately considered, together with the relationship of both.

In gynecological and obstetric research, modeling of a bivariate response comprising of both birth weight and gestational age is recommended. For instance, [10] summarizes findings “that the combination of both variables provides additional information” compared to separate considerations, with regard to mortality. [17] review the research tradition, emphasize the “intimate relation” of birth weight and gestational age such that they could well be regarded as a joint response, and distinguish “prognostic” approaches, where gestational age is used as a covariate, from a “causal” interpretation with an accent on the “temporal nature of gestational age.” The latter seems conclusive, as time is not under control and thus gestational age is indeed not an adjustable influencing factor as it is usually employed in regression, but rather a result of circumstances. [18] state that “low birth weight is a construct of two intricately intertwined components: pre-term delivery and reduced fetal growth, or both” and proceed to analyze them both depending on influencing factors, but with the aim of modeling mortality as a univariate outcome. However, practical research usually aims at a descriptive analysis of birth weight, depending on gestational age and perhaps other factors (e.g., [5, 6]), and so considers a functional relationship and univariate regression (e.g., [8, 9]).

In any such analysis, other parameters than the means are of interest and potentially depend on covariates; e.g., the standard deviation of birth weight may vary between sex. Additionally, the relationship between two outcomes, specifically the strength of dependence between birth weight and gestational age, can itself depend on covariates and this dependence may be non-linear; this is illustrated for our case in Fig. 1, where a measure of dependence varies along covariate levels.

Fig. 1

Rank correlation (Spearman’s rho, x axis) between birth weight and gestational age, depending on certain covariate levels (y axis): The data are split into subsets according to the values of one covariate and the correlation is computed by subset, depicted are the correlations’ confidence intervals with levels 80% (broad line) and 95% (thin line). Left: Cesarian section, two groups; right: maternal gain of weight, four equal subsets bounded by the quartiles. Other covariates do not feature such visible differences between subsets

Therefore, we apply Bayesian distributional copula regression models [19]. Copulas [20] allow the recommended bivariate analysis of birth weight and gestational age, where the two univariate marginal distributions (Gaussian or non-Gaussian) and their dependence structure are estimated simultaneously. All distribution parameters (of the marginals as well as of the copula) are estimated depending on covariates. This approach is more flexible than a classical bivariate regression model with one correlation parameter and the same parametric distribution for both marginals. There is a vast literature on copula modeling in the regression context, see, e.g., references in [19]. Penalized maximum likelihood estimation of copula regression models have been proposed by, e.g., [21, 22]. Another approach for regression problems is to represent the multivariate density by a (D-)vine copula [23, 24].

Especially useful in our situation are non-Gaussian copula families, which assume less symmetries for the data and model upper or lower tail dependence. Likewise, non-Gaussian marginal distributions are useful to model asymmetric data. A great advantage of the Bayesian treatment based on Markov chain Monte Carlo simulations is the direct availability of uncertainty estimates via Bayesian credible intervals. Altogether, such copula models are recommendable for many data situations with unknown or non-linear dependence structures and are widely applicable to bivariate or multivariate biometric analyses in medicine and life sciences, such as those named above. Combined with appropriate marginal distributions and data standardization, they form a natural approach to analyze a bivariate response with an asymmetric joint distribution and skewed marginals as found in our data (Fig. 2).

Fig. 2

Observations of birth weight and gestational age (summarized due to their large number, using the default density estimation of smoothScatter in R; darker shade is for higher density of the point cloud; + stands for a single isolated point)

We adapt this model class to a new situation, perinatal data with two continuous outcome variables, birth weight and gestational age. In the same field, a bivariate copula regression model is developed by [25], conditional on various biometric and clinical variables in a spatial context, but with low birth weight measured as a binary variable. We now investigate, which family of one-parametric copulas, which families of marginal distributions, and which linear predictors are most suitable for the given perinatal registry data. The model choice procedure is outlined in Fig. 3. Using the selected copula model, we estimate the effects of biometric, perinatal, environmental, and socio-economic covariates on birth weight, gestational age, and on their dependence. We compare the copula model to a standard univariate approach, a regression of birth weight depending on gestational age modeled as a polynomial. To this end, the distribution of birth weight conditional on gestational age obtained from the bivariate copula is numerically evaluated using random numbers drawn from it; thus, we preserve more information from the joint analysis than just the marginal. The copula model is further compared to a model that assumes independence between the response components in a simulation study.

Fig. 3

Outline of general procedure to choose optimal marginal and copula families in bivariate Bayesian distributional regression

This article is structured as follows: In Sect. 2, we present the data in more detail, and the applied bivariate copula families, marginal distributions, and the Bayesian distributional regression are outlined. Identification of the best model within this class is reported in Sect. 3. This section also contains our substantive analyses, interpretation of the bivariate copula regression results, identification and evaluation of the univariate polynomial model, and a comparison of both models. Finally, we evaluate the performance of our proposed bivariate model in a simulation study with synthetic data that resemble the observed data. Section 4 discusses some modeling aspects, substantive conclusions from both models, and perspectives. Section 5 summarizes the findings from this article.

2 Methods

2.1 Data Description

The perinatal registry data are collected by all hospitals and are combined and processed by the quality assurance office residing with the state medical association, for the purpose of quality assurance in obstetrical health care. Within our larger “PerSpat” project, we use these secondary data from 2003 until 2014, comprising about 1.7 million records and more than 200 biometric, medical, and social variables on mother and child, pregnancy, birth, and treatment. They are anonymized by removing all personal information apart from the mother’s postal code. Further data cleansing steps are performed, in particular regarding the plausibility of gestational age. Analyses are restricted to singleton births and to children born alive without malformations.

To create an analyzable data subset, we focus on data from a region along the upper course of the river Ruhr in North Rhine-Westphalia, precisely the town of Arnsberg, being of particular interest within the “PerSpat” project. A constrained data analysis also eases computability, as the runtime would have been extremely high otherwise. When restricted to this town, we observe 6442 birth cases within the study period. We remove those where values of relevant variables are not given, leaving a total of 4451 observations.

The response variables are birth weight (measured in g with varying accuracy, mean: 3390, standard deviation: 517) and gestational age (clinically estimated, in days, mean: 277, standard deviation: 12), the former being of primary interest (Fig. 2). Individual relevant covariates are pre-selected from the perinatal registry data. This is done in accordance with the literature (e.g., [7, 8, 12, 17]), and with previous findings within the “PerSpat” project [26]. The specific variables are child’s sex, number of previous pregnancies of the mother, whether the child has been delivered by Cesarean section, whether the birth has been induced, mother’s age, mother’s height, mother’s body mass index (BMI) at the beginning of pregnancy, gain of weight of the mother during pregnancy, number of cigarettes the mother reports to smoke per day, whether the mother is single, and whether the mother is employed. Some descriptive characteristics can be found in Table 1.

Table 1 Descriptive characteristics for covariates from the perinatal data

2.2 Suitable Distribution Families for Copula Regression of Perinatal Data

In this section, we outline the employed statistical method of Bayesian conditional copula models within a distributional regression framework [19]. All models are estimated using a developer version of the BayesX software [27], which implements fully Bayesian inference based on Markov chain Monte Carlo simulation techniques, see [19] for details. We focus on the relevant components for our analysis. For a more general perspective, we refer to [19] and references therein.

To represent our data, let n be the number of observations with bivariate responses $(y_{i1}, y_{i2})$, $i=1, \ldots , n$, from continuous response variables $Y_1$ (birth weight in our case) and $Y_2$ (gestational age). We assume having m covariates $X_{j}$, $j=1, \ldots , m$, with observations $x_{ij}$. We denote probability density functions $f_1$ and $f_2$ and cumulative distribution functions (CDFs) $F_1$ and $F_2$ of $Y_1$ and $Y_2$, respectively.

2.2.1 Copula Distributions

A bivariate copula is defined by a CDF $C_\rho : [0,1]\times [0,1] \rightarrow [0,1]$, such that the joint CDF of $Y_1$ and $Y_2$ can be written as

$$\begin{aligned} F(y_1, y_2) = C_\rho (F_1(y_1), F_2(y_2)) =: C_\rho (u, v). \end{aligned}$$

Sklar’s theorem [28] ensures that $C_\rho$ always exists and is unique for continuous $Y_1$ and $Y_2$, whereas $F_1(Y_1)$ and $F_2(Y_2)$ are uniformly distributed on [0, 1]. With copula density $c_\rho (\cdot , \cdot )$, the joint density of $Y_1$ and $Y_2$ can be written as

$$\begin{aligned} f(y_1, y_2) = c_\rho (F_1(y_1), F_2(y_2)) \cdot f_1(y_1) \cdot f_2(y_2) \end{aligned}$$

and a conditional density as

$$\begin{aligned} f_{1 \mid 2} (y_1 \mid y_2) = c_\rho (F_1(y_1), F_2(y_2)) \cdot f_1(y_1). \end{aligned}$$

(1)

While this representation is unconditional, the results can be extended to the regression context [29].

There are various families of copulas, characterized by a parameter $\rho$ representing the degree and form of dependence between $Y_1$ and $Y_2$. In our analysis, we compare the Gaussian copula family with density

$$\begin{aligned}c_{\rho _N} (u, v) & = \frac{1}{\sqrt{1-\rho _N^2}}\exp \\ & \bigg [-\frac{1}{2}\cdot \frac{\rho _N}{1-\rho _N^2} \Big \{\rho _N(\Phi ^{-1}(u))^{2} -2\cdot \Phi ^{-1}(u)\cdot \Phi ^{-1}(v)+\rho _N(\Phi ^{-1}(v))^{2}\Big \}\bigg ], \end{aligned}$$

$\rho _N \in (-1,1)$, the Clayton copula family with density

$$\begin{aligned} c_{\rho _C} (u, v) = (1 + \rho _C) (u v)^{-1 - \rho _C} \left( u^{-\rho _C} + v^{-\rho _C} - 1\right) ^{-2 - 1 / \rho _C}, \end{aligned}$$

$\rho _C \in (0,+\infty )$, and the Gumbel copula family with density

$$\begin{aligned} c_{\rho _G} (u, v) = \frac{1}{uv} (-\log u)^{\rho _G-1} (-\log v)^{\rho _G-1} \exp \left( -h^{1 / \rho _G}\right) \cdot \left( h^{2 / \rho _G-2} - (1-\rho _G) h^{1 / \rho _G-2} \right) , \end{aligned}$$

where $h:= (-\log u)^{\rho _G} + (-\log v)^{\rho _G}$, $\rho _G \in (1,+\infty )$. As opposed to the Gaussian copula that allows for linear dependence and symmetry only, the Clayton copula allows for non-linear dependence between the two variables, in particular within the region of their extremely low values (tail dependence), whereas the Gumbel copula allows for upper tail dependence [19]. In the Gaussian case, the parameter $\rho _N$ represents the correlation between the two outcome variables. For the other copula models, a higher value of $\rho _C$ (or $\rho _G$, respectively) also signifies a stronger association between them. The copula parameter is also monotonically related to Spearman’s Rho and Kendall’s Tau [21, 30]. For the latter, it holds explicitly: $\tau = {\rho _C}/({\rho _C + 2})$ for the Clayton and $\tau = 1 - {1}/{\rho _G}$ for the Gumbel copula [31].

2.2.2 Marginal Distributions

The two marginal distribution families can be chosen independently from each other and from the copula. Besides the Gaussian distribution $N(\mu , \sigma ^2)$ with mean $\mu$ and variance $\sigma ^2$, a Dagum distribution with density

$$\begin{aligned} \displaystyle f_{p,a,b}(y) = \frac{ap}{y} \cdot \frac{\left( y/b\right) ^{ap}}{\left( \left( y/b\right) ^{a} + 1 \right) ^{p+1}}, \end{aligned}$$

shape parameters $p>0$ and $a>0$ and dispersion parameter $b>0$ is considered in our study.

Within the model choice process, both distribution families (one being symmetric, one skewed and more flexible) are candidates for both response variables, conditional on covariates. But data have to be standardized before, mainly for numerical reasons, but also to adapt them to the Dagum family shape. Standardization does not affect the results, since the original responses can be recovered by linear back-transformation.

Specifically, for $i=1, \ldots , n$, to employ a Gaussian for the marginals, we use data-independent values for mean and standard deviation in a reasonable scale to yield $\displaystyle {\tilde{y}}_{i1}:= (y_{i1} - 3500)/{500}$ for the birth weight and $\displaystyle {\tilde{y}}_{i2}:= ({y_{i2} - 280})/{14}$ for the gestational age. To apply the Dagum marginal (with positive support), birth weight is normalized to $\displaystyle {\tilde{y}}_{i1}:= {y_{i1}}/{500}$, while gestational age is also inverted to a more appropriate shape by $\displaystyle {\tilde{y}}_{i2}:= ({322 - y_{i2}})/{14}$, to have the main part of the data closer to zero and the tail on the right (322 days $=$ 46 weeks exceed the maximum observable gestational age).

2.2.3 Regression Modeling

All these are considered conditional on covariates following [19]. Let $\theta$ represent any single parameter of the joint distribution of $Y_1$ (birth weight in our case) and $Y_2$ (gestational age), i.e., either one of the assumed marginal distributions or of the copula (which means $\theta \in \{\mu ,\sigma ^2, p,a,b, \rho _N, \rho _C, \rho _G\}$ in our case). A linear predictor

$$\begin{aligned} \eta ^{(\theta )} = \beta _0^{(\theta )} + \beta _1^{(\theta )} X_1 + \ldots + \beta _m^{(\theta )} X_m \end{aligned}$$

is formed from the covariates numbered $j = 1, \ldots ,m$, possibly just from a part of them or even reduced to the intercept. Link functions $h_\theta$ such that $\theta = h_\theta ^{-1}(\eta ^{(\theta )})$ are specified appropriately for the respective parameter spaces:

$$\begin{aligned}{} & {} \mu = \eta ^{(\mu )}\text { and} \nonumber \\{} & {} \quad \theta = \exp (\eta ^{(\theta )})\text { for }\theta \in \{\sigma ^2, p,a,b\}\text { as well as} \nonumber \\{} & {} \quad \rho _N = \eta ^{(\rho _N)} \cdot (1+(\eta ^{(\rho _N)})^2)^{-1/2}\text { for the Gaussian copula, } \nonumber \\{} & {} \quad \rho _C = \exp (\eta ^{(\rho _C)})\text { for the Clayton copula and } \nonumber \\{} & {} \quad \rho _G = \exp (\eta ^{(\rho _G)})+1\text { for the Gumbel copula.} \end{aligned}$$

(2)

The covariates to be included to the linear predictor $\eta ^{(\theta )}$ can be separately selected for all parameters $\theta \in \{\mu ,\sigma ^2, p,a,b, \rho _N, \rho _C, \rho _G\}$. We consider those listed in Table 1, without interactions. Many of these covariates are binary. For the others, no obvious non-linear relationships have been found in residual plots beforehand (Figs. 4 and 5).

Fig. 4

Residuals of a linear model with standardized birth weight as univariate response depending on all covariates listed in Table 1, plotted against all non-binary covariates

Fig. 5

Residuals of a linear model with standardized gestational age as univariate response depending on all covariates listed in Table 1, plotted against all non-binary covariates

3 Results

3.1 Bivariate Model Fitting to Perinatal Registry Data

We apply distributional copula regression models (Sect. 2.2) to our perinatal registry data. We evaluate the models using the excerpt of $n=4451$ observations (Sect. 2.1). Besides the BayesX software, calculations have been performed using the R environment [32], with the Dagum distribution from the VGAM package [33] and copula distributions from copula [34].

After preparation steps of data import, cleansing, and standardization, the choice of the optimal copula regression model is a stepwise procedure, outlined in Fig. 3. The copula property enables separate considerations of the marginal distributions of birth weight and gestational age and of their dependence structure. This motivates to identify optimal marginal model fits first and to apply them in the search for the best fitting copula model afterward. Variable selections within this model choice process help to ease later evaluation steps and give a first insight in the relevance of covariates; however, the additional uncertainty has to be kept in mind when considering final results.

Marginal distribution families are chosen by applying Gaussian and Dagum models to both univariate responses. Initially, these four models include all available covariates with respect to all parameters $\theta \in \{\mu , \sigma ^2\}$ or $\theta \in \{p, a, b\}$, respectively; covariates, where the pointwise 95% credible intervals of their respective $\beta _j^{(\theta )}$’s include zero, are removed from the initial model to arrive at an optimal model. The resulting optimal models per family are compared by probability integral transform values, quantile residuals, and log scores. Ultimately, the Gaussian distribution fits best to the birth weight data, and the Dagum distribution for gestational age. Details on these choices can be found in Appendix A.

The optimal marginals are combined with all possible copula families (Gaussian, Clayton, and Gumbel; including rotations); covariates for the copula parameter are selected and these models’ results are compared, whereupon the deviance information criterion (DIC, [35]) and the widely applicable information criterion (WAIC, [36]) are calculated by the BayesX routine (see [19] for the computation from the deviance). Where the evaluation of a model with many covariates is too computationally demanding, specifically for the parameter of non-Gaussian copulas, we pre-select covariates based on the variability of correlation coefficients (the two prominent examples are shown in Fig. 1) and by tentatively adding them one by one. Ultimately, the Clayton copula model yields the best DIC (20 981) and WAIC (21 245) in the sense that finite values are returned by the BayesX routine, while the other copula families lead to no explicit finite results.

In conclusion from the model fitting process, we use a Clayton copula with a Dagum marginal for gestational age and a Gaussian marginal for birth weight. The predictor specifications for each of the six model parameters $\rho _C$, p, a, b, $\mu$ , and $\sigma ^2$ are given in Table 2, the respective link functions specified in Equation system (2) are employed. The final model is evaluated in terms of prediction performance and substantive results in Sect. 3.2.

Table 2 Final bivariate copula model specification and result overview: composition of the linear predictor $\eta ^{(\theta )}$ from the covariates, per parameter $\theta \in \{\mu ,\sigma ^2, p,a,b, \rho _C\}$ of the chosen marginal and copula families, together with the employed link functions

3.2 Analysis of Perinatal Registry Data

Based on the results from Sect. 3.1, we apply the bivariate distributional copula regression model (see specification in Table 2) to the perinatal registry data (Sect. 2.1). A standard univariate regression approach for birth weight is set up for comparison.

3.2.1 Evaluation of Copula Regression Model

Influences of covariates on birth weight’s mean are quantified in Table 3. Apart from this, covariates also influence other model parameters (see overview in Table 2). The birth weight’s scale ($\sigma ^2$) is higher for male children, in the case of Cesarean section, for higher maternal BMI and if the mother smokes.

Table 3 Regression coefficients (posterior mean and pointwise 95% credible interval, in bold where the latter does not include zero) regarding the parameter $\mu$ of (standardized) birth weight, estimated in the polynomial and the copula distributional regression model

For the Dagum distribution of gestational age, the shape parameter p is higher in the case of induction and lower in the case of Cesarean section. The shape parameter a increases with the maternal gain of weight and is lower in the case of Cesarean section, induction, and if the mother smokes. The scale parameter b increases with the number of previous pregnancies and in the case of Cesarean section, and is lower in the case of induction. If we consider the distribution’s median $b\cdot (-1 + 2^{1/p})^{-1/a}$, the monotonically increasing link functions and the inverting transformation $\displaystyle {\tilde{y}}_{i2} = ({322 - y_{i2}})/{14}$ of the data, we can qualitatively interpret these results such that gestational age is higher for decreasing p or b or increasing a, e.g., with increasing maternal gain of weight. But we also see that this interpretation is generally rather difficult. It leads to no consistent results in terms of monotone effects for Cesarean section or induction.

For the copula parameter, only the information, whether the child has been delivered by Cesarean section, emerges as a stably estimated influence. Taking the intercept into account, the dependence between birth weight and gestational age measured in this way turns out to be surprisingly weak, in fact not far from independence: $\rho _C\approx 0.40$, 95%-CI: [0.21, 0.76] for children delivered by Cesarean section, $\rho _C\approx 0.14$, 95%-CI: [0.09, 0.22] for the others ($\rho _C \searrow 0$ would signify independence).

3.2.2 Univariate Polynomial Regression

Instead of bivariate regression for birth weight and gestational age, separate univariate analysis is common in gynecological and obstetric research (e.g., [5,6,7]), perhaps adjusted for the other, or with a dichotomous response like “small for gestational age” (e.g., [11, 12]).

We confirm a regression model as the most suitable among univariate birth weight models, where gestational age is included as a covariate in the form of a polynomial $p_\gamma$ of degree three: To find this, we apply fractional polynomial [37] regression models

$$\begin{aligned} y_{i1} = \beta _0 + p_\gamma (y_{i2}) + \sum _{(\text {Cov. }j\text { incl.})}^{j=1, \ldots , m} \beta _j x_{ij} + \epsilon _i, \qquad i = 1, \ldots , n, \end{aligned}$$

with independent $\epsilon _i \sim N(0, \sigma ^2)$, for birth weight, with observed gestational age $y_{i2}$ as covariate and some of the further covariates (see Table 1). Among the usual fractional polynomials of degree one or two, the resulting mean prediction errors are very close to each other. With regard to residual sum of squares, Akaike information criterion [38], Bayesian information criterion [39], and maximum prediction error (i.e., for outlying data), the polynomial $p_\gamma (y_{i2}) = \gamma _1 y_{i2}^2 + \gamma _2 y_{i2}^3$ performs best. However, a model of higher degree with “full” polynomial

$$\begin{aligned} p_\gamma (y_{i2}) = \gamma _1 y_{i2} + \gamma _2 y_{i2}^2 + \gamma _3 y_{i2}^3 \end{aligned}$$

is even better in this respect, is in accordance with gynecological and obstetric literature (e.g., [8, 9]) and therefore preferred.

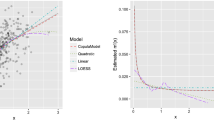
The obtained regression coefficients regarding both gestational age and covariates are shown in Table 3. According to these, all polynomial terms are relevant, i.e., their regression coefficients’ pointwise 95% credible intervals do not include zero. This is further illustrated by Fig. 6 showing the regression curve of the simplified model $y_{i1} = \beta _0 + \gamma _1 y_{i2} + \gamma _2 y_{i2}^2 + \gamma _3 y_{i2}^3 + \epsilon _i$, in which the non-linear trend of birth weight on gestational age is detected, but it becomes also evident that valid predictions are not possible outside the essential range of data.

Fig. 6

Observations of birth weight and gestational age (summarized due to their large number, using the default density estimation of smoothScatter in R; darker shade is for higher density of the point cloud) with a polynomial regression curve of degree three

3.2.3 Comparison of Standard Univariate and Copula Approach

The comparability of the bivariate copula model and the standard univariate polynomial model is limited. A purely numerical comparison reported here should not be interpreted too deeply, as only a one-dimensional extract of the full copula result is considered, see the respective interpretations and discussions of both models’ features in Sect. 4.3. The two-dimensional predictive performance of the copula model is illustrated by a simulation study reported in Sect. 3.3. Results show the advantage of distributional copula regression, when the dependence structure depends on a covariate, while there is no loss when it does not, and a copula model performs only marginally worse when the data are indeed independent.

One quantifiable comparable outcome are predictions of birth weight conditional on gestational age. They are obtained from the copula model, after the bivariate joint distribution is estimated: To evaluate the conditional distribution with density (1), we draw random numbers via rejection sampling with a uniform envelope extended to a large enough range. Thereby, we use the observed gestational age values $y_{i2}$, parameter estimates $\hat{\theta }$ obtained from samples of the posterior $\hat{\beta }_j^{(\theta )}$’s, and the covariate values of the respective observations.

We compare the obtained prediction samples of birth weight from copula and standard model with the observed values using logarithmic scores (log-scores, [40]). To obtain out-of-sample prediction errors, we implement a four-fold cross-validation, for which the observations are randomly assigned to subsamples of equal size. Using the estimated model based on three subsamples, individual log scores for the respective left-out subsample are computed using the R package scoringRules [41], where a lower score represents a better fit.

For the standard model, there results an log-score of 7.41; for the copula model, with respect to the birth weight response conditional on gestational age, it is 7.67. Thus, the copula model performs only slightly worse than the standard model (cf., Sect. 4.3 for an assessment of this result).

The model predictions are also compared directly with the help of graphical evaluation. For the vast majority of birth weight predictions, the distributional copula regression model is close to univariate polynomial regression. The residual and comparison plots in Fig. 7 show how the models agree, especially in mean (bottom left). However, extremely low birth weights are correctly predicted by the polynomial alone (top left), while their observations diverge from the copula model predictions (top right, fitted values are in the range of the main part of data, but residuals are too far to the negative). A closer range of predictions from the copula model is also visible (top right). The residual plot for gestational age from copula regression (Fig. 7, bottom right) also reveals rather poor predictions of extremely low values, which often coincide with very low birth weights; besides, there emerge two distinguishable groups of gestational age predictions, presumably in connection with the highly influential Cesarean section and induction covariates. Due to independent and simultaneous estimation of marginals and copula, estimates of the regression coefficients with regard to birth weight’s mean are very similar in both models, but their relevance (i.e., whether a pointwise 95% credible interval does not include zero) differs (Table 3).

Fig. 7

Top: residual plots for birth weight from polynomial (left) and copula distributional (right) regression model, each with smoothed mean and standard deviation lines; bottom right: the same for gestational age from copula model; bottom left: predictions of birth weight from polynomial and copula distributional regression model, plotted against each other per observation, with bisecting line (dotted) and robustly estimated principal axis of the plotted data (“direction of main point cloud”, solid); predictions for all figures obtained from cross-validation study

3.3 Simulation Study on Bivariate Modeling

The considerations on the copula model’s predictive performance are completed by a simulation study comparing actual bivariate models, as opposed to the comparison with a univariate standard model.

A Gaussian marginal distribution for simulation of standardized birth weight and a Dagum marginal distribution for standardized gestational age are applied in any case. The corresponding regression coefficients’ posterior means from the original marginal fitting are applied as “true” marginal regression coefficients.

We simulate bivariate response data

• (i) independently,

• (ii) from a Clayton copula with a parameter $\rho _C = 2$ for all observations or

• (iii) from a Clayton copula with a parameter depending on the Cesarean section covariate: strong dependence ($\rho _C = 5$) in the case of Cesarean section and weak dependence ($\rho _C = 0.5$) otherwise.

(An example of the resulting response data is shown in Fig. 8.)

Fig. 8

One simulation of bivariate response data distinguished by Cesarean section covariate: left: independently sampled; center: from a Clayton copula with a parameter $\rho _C = 2$ for all observations; right: from a Clayton copula with a parameter depending on the Cesarean section covariate: strong dependence ($\rho _C = 5$) in the case of Cesarean section (below) and weak dependence ($\rho _C = 0.5$) otherwise

For each case (i)–(iii) we fit three models, with one matching the simulated case each:

• (i) independence, i.e., separate fitting of the two response variables,

• (ii) a Clayton copula model with only an intercept, and

• (iii) a Clayton copula model including Cesarean section

using BayesX. The following steps are conducted for each case (i)–(iii) and each fitted model (I)–(III) using 100 training data sets with 500 observations each.

• (I) Derivation of model marginal distributional parameters ($\mu$, $\sigma ^2$, p, a, b) and if present also the copula parameter using respective MCMC samples.

• (II) Derivation of predictive performance on a test data set of the same size using energy scores [41] using the function es_sample from the R package scoringRules.

Results for the predictive scores are visualized in Fig. 9.

Fig. 9

Loss in prediction performance of incorrect bivariate copula regression models (I: independence, II: Clayton with intercept only, III: Clayton with parameter depending on a covariate) from one-hundred simulations. The energy scores of the six fits with incorrect models (i.e., i/II, i/III, ii/I, ii/III, iii/I, iii/II) are transformed to relative changes compared to the scores of the correct model for the respective data set. (Scores of i/I, ii/II, and iii/III are then expressed as zero)

We are mainly interested in the distributional copula regression model (III), where the dependence parameter is assumed to depend on a covariate. It performs clearly better than the others, when the data actually exhibit such a dependence structure (Fig. 9, right). If they are simulated from a copula model, but with a constant copula parameter (center), then the application of model (III) leads to no relevant loss compared to the correct model (II). The only weakness of model (III) is found, when the two response variables are actually independent (left): Both marginals are influenced by Cesarean section, which leads to two groups of data in the two-dimensional space with respect to this covariate; further covariates may influence the shape of the groups. In this case, model (III) presumes a dependence structure with some difference between these groups, which may then be estimated by chance. Another aspect is that models (II) and (III) always estimate finite regression coefficients, so that the exponential link function leads to a small but positive dependence parameter, even if it should actually be zero.

4 Discussion

4.1 Data Quality

The secondary data from the perinatal registry have not originally been collected to be scientific material, but for quality assurance. As such, they are nonetheless very informative with regard to procedures in obstetric health care, like the birth mode (Caesarian section, induction), which turns out as an important covariate. On the other hand, measurement accuracy varies (e.g., one hospital measures birth weight accurate to 1 g, another to 10 g). For gestational age, data are subject to uncertainty of reporting, measurement, clinical estimation, and documentation (e.g., [11]), although we have carefully checked ours for plausibility. Maternal smoking is self-reported and perhaps biased toward a socially desirable answer; nonetheless, these data are accurate enough such that an effect of smoking in line with other studies from the literature (see Sect. 4.3) is detected despite the remaining noise.

4.2 Gestational Age and Dependence Structure

There are strong effects of all three polynomial terms of gestational age in the univariate model and the increasing trend of the mean birth weight along gestational age decreases again toward the end (cf., Fig. 6). This phenomenon is also reported in other studies (e.g., [5]) and could be an effect of medical decisions to deliver fetuses with high weights rather early by induction or Cesarean section and to avoid such treatments for a longer time when fetal weight is low.

Tail dependence is likely to be found in the data, specifically in the region of pre-term births and low birth weight, but it can be comparatively weak, and the data are also affected by other complex structures, especially in the region of high gestational age. It is possible that the slight decrease of the mean birth weight (as shown by the polynomial model) prevents the copula model from being fitted in a way that the lower tail is well represented. The available copula models assume only one tail and a certain symmetry with respect to its axis, while the data exhibit something like a second tail toward a different direction.

Against this background, our estimation of tail dependence is very sensitive to gestational age observation. Any data inaccuracies, which are generally possible for gestational age (e.g., [11]), have an impact on regression models.

4.3 Model Comparison and Evaluation

The reported numerical comparison of the copula model and the standard polynomial model is limited. The copula model is more general in the sense that it is intended for jointly modeling a bivariate response. A univariate model is a simpler approach than a joint analysis of a bivariate outcome. Nevertheless, the polynomial model can produce useful results and realistic predictions, but only regarding birth weight alone. It is more specialized but unsuitable for statements on birth weight and gestational age as a joint quantity.

Concerning the copula model’s prediction accuracy in tails, there are not so many observations compared to the very large number of births in the center of the distribution. By regression, predictions of gestational age tend naturally toward the center, such that, if the copula results are reduced to the conditional form, birth weight predictions follow them accordingly.

An important benefit of the distributional copula regression model are visible differences between groups, with respect to both scale and dependence: Fig. 10 shows examples of predictions, distinguished by sex and Cesarean section. It becomes apparent, that the variability and structure of the response data is deeper explained, when influences of covariates on more parameters than only the means are allowed—unlike in a standard regression model.

Fig. 10

Bivariate density of birth weight and gestational age, as predicted from copula model with posterior means of all parameters plugged in, conditional on certain selected exemplary covariate levels (the others are fixed to: maternal height: ${170}\,\hbox {cm}$, maternal BMI: ${20}\,\hbox {kg}\,\hbox {m}^{2}$, maternal gain of weight: ${10}\,\hbox {kg}$; and all others set to “no” or 0, respectively)

Considering both models together, we obtain conclusions that go beyond effects of covariates on birth weight. A striking example are the relationships between birth weight, gestational age, and the Cesarean section covariate (cf., Tables 2 and 3): The latter has an influence on birth weight according to the copula model, where gestational age is separately estimated, while this does not hold for the standard model, where gestational age is present as an influential covariate. The Cesarean section covariate also influences the parameters of the Dagum distribution of gestational age in the copula model as well as the copula parameter. According to these results, the influence of the Cesarean section covariate is in fact manifold (cf., e.g., [42]), but this can only be discovered using the bivariate model, which provides more extensive conclusions in this respect. In the standard model, the importance of the Cesarean section covariate disappears; it is presumably predominated and in parts mediated by gestational age, with which Cesarean section is correlated. Conversely, Cesarean section can have a relevant effect when gestational age is not included in the birth weight marginal regression of the copula model. Similar considerations hold for the induction covariate.

As a different example, both models agree with respect to the effect of smoking on birth weight (Table 3). There is also an effect on gestational age found in the bivariate model (Table 2), but only with respect to one Dagum parameter and, thus, presumably less important. So, there seems to be no mediation by gestational age in the standard model. The influence of smoking on both birth weight and gestational age as well as on the risk of pre-term birth or “small for gestational age” has also been found in many studies with univariate responses (e.g., [11, 43, 44]).

4.4 Modeling Perspectives

The employed Dagum distribution fits fairly well to our strongly asymmetric gestational age data, when compared to the Gaussian distribution. With its three parameters, it is flexible enough to be fitted to positive data with inconvenient shapes and, thus, it is a good choice among the options implemented in the BayesX routine. Other families could be possible too, but should be just as flexible and, therefore, have several parameters including shape, even when the parametrization is unfavorable for substantial interpretation.

Also, other copula families as well as specific data transformations might be useful for complicated bivariate response data shapes as ours, e.g., the skewed t-copula allows for strong asymmetry and non-linearity [45], but estimation and interpretation of the multiple parameters are inconvenient compared to our one-parametric representation of dependence structure.

As there remains much noise after either model fit, more complex generalized additive models, especially using splines, could be considered where non-linear relationships are possible [46]. This holds also for the spatial dimension in future studies when larger regions are considered. There, further information such as neighborhood could be used. Since lower birth weights are observed in some urban regions, an according spatial dependence structure can also be included. This and other model enhancements may ease the detectability of very weak effects, which is an important aspect within our larger “PerSpat” project.

Extremely low values, i.e., very early pre-term births and cases of very low birth weight, are not so well reflected in the applied models’ results, as the main part of the data seems to predominate the fitting. The focus of the present study is to model the complete distribution of typical birth data, without special weight of extreme categories, although the latter are of clinical concern. The prediction results for extremely low values lead to the conclusion that another study design where such cases are up-weighted should be chosen in future research.

5 Conclusions

For regression analyses regarding birth weight, the bivariate modeling jointly with the gestational age emerges as very productive. The results allow insights into the relationships between these two variables and others, e.g., Cesarean section, avoiding mediation.

Distributional regression, where any parameter of the bivariate distribution is estimated conditional on covariates, is an appropriate instrument to explain the variability and structure of the perinatal registry data in more depth. While a Gaussian distribution is well fitted to the marginal birth weight data, the heavily skewed gestational age data are better modeled by the more flexible Dagum distribution. Effects of many explanatory variables on both birth weight and gestational age can be distinguished. A copula model is useful to simultaneously estimate the dependence structure and the marginals. The perinatal data are fitted better by the lower tail Clayton copula than by the Gaussian and the Gumbel. However, the estimated dependence is weak.

Appendix A: Details on Marginal Specifications

The determination of optimal marginal distributions among the options available in the BayesX software (cf., [47]) is based on an overall consideration of several aspects including interpretability and simplicity. Our decisions are initially based on log-scores representing statistics on predictive performance, and are supported by visual evaluations of goodness of fit.

The univariate distributional models are fitted and compared using log scores (cf., Sect. 3.2.3). The log scores for Dagum and Gaussian distribution are very close to each other in the case of birth weight (Dagum: 7.63, Gaussian: 7.66); however, for gestational age, the Dagum distribution has a notably better fit (3.74 vs. 4.07).

These findings are confirmed by graphical evaluation of the probability integral transform values $F(y; \hat{\mathbf {\beta }})$ (Fig. 11) and the corresponding normalized quantile residuals $\Phi ^{-1}(F(y; \hat{\mathbf {\beta }}))$ (Fig. 12, cf., [48]), where posterior means of the respective $\beta _j^{(\theta )}$’s are employed and y (birth weight or gestational age) is on the standardized scale. The theoretically expected uniform distribution of the $F(y; \hat{\mathbf {\beta }})$’s is well recognizable for the Dagum fits, while it is strongly violated for the Gaussian fit of gestational age data; a similar non-uniform structure as for the latter remains also for the Gaussian fit of birth weight data, but considerably weaker. The quantile–quantile plot of the $\Phi ^{-1}(F(y; \hat{\mathbf {\beta }}))$’s shows a slightly better fit of the Dagum model in either case, especially in the lower range, but more striking for gestational age, where a distinguishable structure remains for the Gaussian. These results are convincing to use the Dagum distribution for the gestational age marginal in the analyses.

Fig. 11

Histograms of probability integral transform values $F(y; \hat{\beta })$ (with posterior means of the $\beta$’s plugged in) for the two models and the two marginal response variables

Fig. 12

Quantile–quantile plots of randomized quantile residuals $\Phi ^{-1}(F(y; \hat{\beta }))$ (with posterior means of the $\beta$’s plugged in) for the two models and the two marginal response variables

For birth weight, however, the results are less clear and there are reasons to stick with the Gaussian, in doubt: In this application, we are primarily interested in influences of covariates on mean and variability of birth weight, and these characteristics are directly represented by the $N(\mu , \sigma ^2)$ parametrization, such that effects of covariates are easily and directly interpretable. By contrast, the interpretation of effects on the three Dagum parameters is quite complicated and sometimes ambiguous in terms of substantive results (cf., Sect. 3.2.1). Results from the Gaussian fit are furthermore directly comparable to other studies, especially with standard regression models. So, as there is at least some evidence above that the Gaussian family does not fit essentially worse than the other, we use it for the birth weight marginal in the analyses.