1 Introduction

As there is almost no prior published work on the design of tandem bicycle frames that considers the topic scientifically, the goal of this paper is to address this lack. In general, bicycle design addresses conflicting requirements: low mass and good aerodynamics but also high stiffness and strength. In particular, high torsional stiffness is desirable, as this both reduces stored elastic strain energy and improves handling under high imposed loads, e.g. in a racing start.

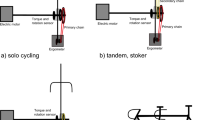
Eight out of 51 Paralympic cycling events are contested on tandem bicycles: visually impaired para-cyclists ride as “stoker” for a sighted “captain” with pedalling synchronised by a “timing chain” (usually on the frame left with final drive on the right). Tandems must resist higher loading than solo bicycles over a longer wheelbase, yet must still fit between the legs of the riders. UCI rules [1] restrict solo bicycles to a “diamond” topology with three main tubes: “seat”, “down” and “top”. Tandems need a second seat tube and at least two further tubes: a rear top tube and a bottom tube between bottom brackets (Fig. 1a). Common designs include further members (Fig. 1b–d), but no single topology has yet predominated nor been mandated [1]. Studies on aerodynamic drag of bodies in-line [2] and solo bicycles [3] suggest that the additional members, although improving stiffness and strength, will increase air resistance (and certainly add mass). There is little literature on tandem design. Oliver [4] and Ballantine and Grant [5] both define various tandem topologies (e.g. Fig. 1). However, discussion of their relative merits is anecdotal, not scientific. Sharp [6] did show (as early as 1896) how graphical methods can be used to determine forces in a tandem, but only for in-plane vertical loading of a fully triangulated frame. Sharp acknowledged that rider-imposed twisting was a more important load case, but offered no method to calculate either loads or response. For many decades, the design of all bicycles was by empirical development. The first published theoretical analyses of the structural behaviour of bicycle frames appear to be by Davis and Hull [7] and Soden et al. [8] in the 1980s. Both used finite element analysis (FEA). Increasing computer power has since made more sophisticated analyses possible. Much work will have remained proprietary; nevertheless, there are now a number of published analyses of bicycle frames, e.g. [9,10,11,12,13]. FEA is now a key tool in bicycle design, but useful results require realistic boundary conditions. An ISO standard [14] specifies safety test requirements for bicycles, but does not detail scalable loads that are a close approximation to actual use. In situ measurement of all forces acting on a bicycle requires a full set of transducers (instrumented pedals, handlebars and seatpost); e.g. [15,16,17,18,19]. These are not generally available to designers without access to a sports science laboratory. The alternative is to estimate forces based on a reduced set of measurements. In this regard, Soden and Adeyefa’s 1979 work [20] was seminal: forces applied by a cyclist to pedals and handlebars during “speeding, hill climbing and starting” were estimated by calculations based on data from cine films; pedal loads were found to be within 20% of measurements using strain gauged pedals (handlebar forces were not measured). However, although the paper has been cited ~ 200 times [21], none of these concern tandems. Torque applied by a cyclist can now be readily measured with a “power meter”, but the literature is not explicit on how a designer can use this data to find corresponding forces directly acting on the bicycle frame via bottom bracket bearings, handlebars and wheel axles. In particular, there is nothing relating to tandems with their complications of two cyclists and additional chain. This paper addresses this gap. A method to determine the loads on a tandem bicycle frame is presented. The only inputs required are dimensions, masses and the torques applied by the riders. The method is validated by comparing calculated forces on individual riders with literature measurements [16, 20]. Results are presented for selected tandem case studies and implications for design discussed. The obtained loads are used to evaluate the performance of four common tandem designs (Fig. 1).

Fig. 1
figure 1

Tandem frame topologies: a open; b double diamond; c direct lateral; d marathon

Full size image

2 Method

2.1 Load case calculation

Soden et al. [8, 20] showed that the highest loads, and stresses, in a bicycle occur in starting: when a cyclist applies maximal forces to the pedals to achieve the highest possible acceleration. The following method focuses on this case for a tandem. Riders are assumed to be unseated, with cranks horizontal and shoes clipped into pedals.

2.1.1 System equilibrium

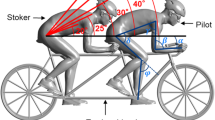
Figure 2a shows external forces and key dimensions for the system of tandem and cyclists. D’Alembert forces at the centres of mass (CoM) of riders and bicycle allow the problem to be treated as one of static equilibrium.

Fig. 2
figure 2

Schematic views of a tandem frame, b rearmost cyclist (stoker) showing key dimensions, external forces, wheel/ground contact points (1, 2) and bottom brackets (B_C, B_S)

Full size image

A timing chain connects the pedal cranks of captain and stoker and thus the total torque acting on the chainring driving the rear wheel (neglecting losses [2]) is

$$Q={Q}_{{\text{c}}}+{Q}_{{\text{s}}},$$
(1)

where \({Q}_{{\text{c}}}\) and \({Q}_{s}\) are the input torques provided by the captain and stoker, respectively.

Rear wheel traction:

$${F}_{2}=\frac{Q}{G{R}_{{\text{w}}}},$$
(2)

where G is the gear ratio (for velodrome racing a fixed gear ratio is used, e.g. G = 3.86 for a 54- and 14-tooth chainring and sprocket) and \({R}_{w}\) is the rear wheel radius.

Total mass is the sum of the captain \({m}_{c}\), stoker \({m}_{s}\) and bicycle \({m}_{b}\):

$${m}_{{\text{t}}}={m}_{{\text{c}}}+{m}_{{\text{s}}}+{m}_{{\text{b}}}.$$
(3)

The output acceleration is

$$a=\frac{{F}_{2}}{{m}_{{\text{t}}}}.$$
(4)

Taking moments about the rear wheel/ground contact point 2:

$${N}_{1}{l}_{12}+{m}_{{\text{s}}}a\left({h}_{{\text{B}}}+{h}_{{\text{gs}}}\right)+{m}_{{\text{c}}}a\left({h}_{{\text{B}}}+{h}_{{\text{gc}}}\right)+{m}_{{\text{b}}}a{h}_{{\text{gb}}}={m}_{{\text{s}}}g\left({l}_{{\text{Bs}}}+{l}_{{\text{gs}}}\right)+{m}_{{\text{c}}}g\left({l}_{{\text{Bc}}}+{l}_{{\text{gc}}}\right)+{m}_{{\text{b}}}g{l}_{{\text{gb}}}.$$
(5)

Resolving vertically,

$${N}_{1}+{N}_{2}={m}_{{\text{t}}}g.$$
(6)

2.1.2 Rider equilibrium

Figure 2b shows the key dimensions and forces acting on the stoker (note subscript s). The cyclist is standing on, and clipped into, the pedals and not in contact with the seat. The position of the CoM is defined relative to the bottom bracket BS; this may be calculated by division of the body mass into proportional segments, see e.g. Clauser et al. [22]. The cyclist is accelerating horizontally at rate a, but is otherwise in static equilibrium.

The input torque \({Q}_{s}\) is applied by the rider’s pedal forces

$${Q}_{s}=\left({P}_{sl}+{P}_{sr}\right){R}_{p}.$$
(7)

The cranks are horizontal and the left pedal is forward. The rider is pulling up on the right pedal.

Moment equilibrium requires that the horizontal handlebar forces must be equal. There are no significant horizontal forces at the pedals (consistent with the measurements of Soden and Adeyefa [20] and Hull [15, 16]); thus,

$${F}_{s}={m}_{s}a.$$
(8)

The net vertical pull-up on the handlebars (from both arms) is

$${\Delta H}_{{\text{s}}}={H}_{{\text{sl}}}-{H}_{{\text{sr}}},$$
(9)

where the rider is pulling up on the left and pushing down on the right handlebar.

Taking moments about the bottom bracket Bs:

$${\Delta H}_{s}=\frac{{Q}_{{\text{s}}}+{m}_{{\text{s}}}a\left({h}_{{\text{gs}}}-{h}_{{\text{hs}}}\right)-{m}_{{\text{s}}}g{l}_{{\text{gs}}}}{{l}_{{\text{hs}}}}.$$
(10)

Typically, in a maximal effort, the rider’s CoM position is not sufficient to provide their torque \({Q}_{s}\) and they must also pull upwards on the handlebars, i.e. \({\Delta H}_{s}\) is positive.

The net downward pedal force is:

$${\Delta P}_{{\text{s}}}={P}_{{\text{sl}}}-{P}_{{\text{sr}}}={m}_{{\text{sg}}} +{H}_{{\text{sl}}}-{H}_{{\text{sr}}}={m}_{{\text{sg}}} +{\Delta H}_{{\text{s}}}.$$
(11)

Using (7), the output left and right pedal forces are:

$${P}_{{\text{sr}}}=\frac{1}{2}\left(\frac{{Q}_{{\text{s}}}}{{R}_{{\text{p}}}}-{\Delta P}_{{\text{s}}}\right)$$
(12)

and

$${P}_{{\text{sl}}}=\frac{{Q}_{{\text{s}}}}{{R}_{{\text{p}}}}-{P}_{{\text{sr}}}.$$
(13)

The x (longitudinal) axis rotational equilibrium of a rider requires that the torque of forces at the handlebars balances the torque of the left/right pedal forces:

$$\left({{H}_{{\text{sl}}}+{H}_{{\text{sr}}})w}_{{\text{hs}}}={(P}_{{\text{sl}}}+{P}_{{\text{sr}}}\right){w}_{{\text{p}}}.$$
(14)

Substituting (9) into (14), an expression can be found for the output right-hand handlebar force:

$${H}_{{\text{sr}}}=\frac{1}{2}\left({(P}_{{\text{sl}}}+{P}_{{\text{sr}}})\frac{{w}_{{\text{p}}}}{{w}_{{\text{hs}}}}-{\Delta H}_{{\text{s}}}\right).$$
(15)

The output left-hand handlebar force \({H}_{sl}\) can then be found using (9).

Using Eqs. (10–13), (15) and (9), we can calculate the left and right, pedal and handlebar forces for the stoker. The same equations can be applied to the captain, with substitution of subscript c for s. Note that these equations for rider forces are not exclusive to the case of a tandem and will be validated by literature measurements for solo cyclists [12, 16].

2.1.3 Bottom bracket equilibrium

Consider the stoker bottom bracket Bs (Fig. 3a). On a tandem, this assembly usually carries both drive and rear timing chainrings. The bearing forces, \({S}_{xl},\) etc., are unknowns that are outputs of the following equations.

Fig. 3
figure 3

Plan, elevation and rear views of a rear bottom bracket and b rear wheel showing key dimensions and external forces

Full size image

Drive and timing chain tensions, \({T}_{d}\) and \({T}_{t}\), are found from the relevant torques and chainring radii \(:\)

$${T}_{d}=\frac{Q}{{R}_{d}},$$
(16)
$${T}_{t}=\frac{{Q}_{c}}{{R}_{t}}.$$
(17)

Taking moments about the z axis, about the right-hand bearing:

$${S}_{{\text{xl}}}=-{T}_{{\text{t}}}\left(\frac{1}{2}+\frac{{w}_{{\text{t}}}}{{w}_{{\text{BB}}}}\right)-{T}_{{\text{d}}}{\text{cos}}\theta \left(\frac{{w}_{{\text{d}}}}{{w}_{{\text{BB}}}}-\frac{1}{2}\right).$$
(18)

The angle \(\theta\) of the chain from the horizontal must be determined from the dimensions of the frame, chainring and sprocket.

Resolving horizontally:

$${{S}_{{\text{xl}}}+S}_{{\text{xr}}}+{T}_{{\text{t}}}={T}_{{\text{d}}}{\text{cos}}\theta .$$
(19)

Similarly, taking moments about the x axis about the right-hand bearing and resolving vertically:

$${S}_{{\text{zl}}}={P}_{{\text{sl}}}\left(\frac{{w}_{{\text{p}}}}{{w}_{{\text{BB}}}}+\frac{1}{2}\right)+{P}_{{\text{sr}}}\left(\frac{{w}_{{\text{p}}}}{{w}_{{\text{BB}}}}-\frac{1}{2}\right)-{T}_{{\text{d}}}{\text{sin}}\theta \left(\frac{{w}_{{\text{d}}}}{{w}_{{\text{BB}}}}-\frac{1}{2}\right)$$
(20)

and

$${{S}_{{\text{zl}}}+S}_{{\text{zr}}}+{P}_{{\text{sr}}}={{P}_{{\text{sl}}}+T}_{{\text{d}}}{\text{sin}}\theta .$$
(21)

For the captain’s bottom bracket, we may reuse (18–21), but with substitution of symbol C for S for the output forces and subscript c for s. Note also that there is no drive chain, and the timing chain tension is reversed.

2.1.4 Rear wheel equilibrium

Figure 3b shows the key dimensions and external forces acting on the rear wheel. Note that the weight of the wheel is neglected (typically, this might be ~ 15N compared to a chain tension of more than 4 kN).

The output vertical (z) components of the forces from the frame acting on the rear wheel axle can be found by taking moments about the x axis:

$${A}_{{\text{zr}}}=\frac{{N}_{2}}{2}+{T}_{{\text{d}}}{\text{sin}}\theta \left(\frac{1}{2}+\frac{{w}_{{\text{d}}}}{{w}_{{\text{oln}}}}\right).$$
(22)

Resolving vertically:

$${{A}_{{\text{zl}}}+A}_{{\text{zr}}}={N}_{2}+{T}_{{\text{d}}}{\text{sin}}\theta .$$
(23)

The output horizontal (x) components can be found in a similar manner:

$${A}_{{\text{xr}}}=\frac{{F}_{2}}{2}+{T}_{{\text{d}}}{\text{cos}}\theta \left(\frac{1}{2}+\frac{{w}_{{\text{d}}}}{{w}_{{\text{oln}}}}\right),$$
(24)
$${{A}_{{\text{xl}}}+A}_{{\text{xr}}}={F}_{2}+{T}_{{\text{d}}}{\text{cos}}\theta .$$
(25)

2.2 Boundary conditions on frame

The method above provides a set of forces applied to the frame at handlebars, bottom brackets and rear axle. These forces, including weight \({m}_{{\text{b}}}g\), d’Alembert inertial force \({m}_{b}a\) and front wheel reaction\({N}_{1}\), are in static equilibrium. A subset of this complete set of forces may be used as a load case for FEA of a frame, in combination with an appropriate set of displacement constraints that eliminate rigid body motions. Acceleration \(a\) and reaction \({N}_{1}\) are obtained from Eqs. (1–5). Equations (9–13 and 15) provide the left and right, pedal and handlebar forces for both stoker and captain. Bottom bracket forces are determined using Eqs. (16–21).

Forces and constraints may be applied as shown in Fig. 4a. This approach eliminates fork and handlebars from the model by use of remote loads applied to relevant points on the frame. \({N}_{1}\) and the front handlebar forces act on the frame head tube (load paths are via fork steerer and headset bearings). Stoker handlebars are typically attached to the captain’s seat post; in this case, the stoker handlebar forces are applied as remote loads to the top of the captain’s seat tube. Bottom bracket bearing forces are applied directly to the surfaces within the frame shells (see also Fig. 5a). \({m}_{{\text{b}}}g\) and \({m}_{b}a\) are distributed loads on the entire frame. x, y and z displacement constraints, with y rotation unrestrained, are applied at both the rear wheel axle points (see also Fig. 5b). This prevents all rigid body translations and rotations about the x and z axes, eliminates rear axle forces from the model and approximates the clamping of the rear wheel axle into the frame. The only remaining degree of freedom is rotation about the y axis (at the rear axle); this is eliminated by preventing z displacement for a point on the head tube (since all applied loads are in static equilibrium, this constraint carries no load but is necessary to eliminate a rigid body motion).

Fig. 4
figure 4

a Forces and boundary conditions and b main dimensions (mm) for a finite element analysis of a tandem bicycle frame (tube wall thickness is 2 mm throughout)

Full size image
Fig. 5
figure 5

Details of finite element mesh and boundary conditions in areas of a stoker bottom bracket (with bearing forces), and b rear dropouts (with cylindrical surface displacement constraints, rotation unrestrained)

Full size image

2.3 Example application

A base case is considered of two endurance athletes starting on a tandem. Each rider is making a maximal starting effort of 250 Nm with the left pedal forward. Table 1 and Fig. 4b give the full set of variables used.

Table 1 Base case input variables
Full size table

Four other cases are considered for comparison:

  1. 1.

    Right pedal forward start.

  2. 2.

    Timing chain on right-hand side (\({w}_{{\text{t}}}\) = − 45 mm, \({w}_{{\text{d}}}\) = 50 mm).

  3. 3.

    Solo bicycle start \(({Q}_{{\text{c}}}\) = 0, \({m}_{{\text{c}}}\) = 0, \({m}_{b}\)= 8 kg, \({l}_{12}\) = 1055 mm).

  4. 4.

    2g constant speed turn (g replaced by 2\(g\), \({Q}_{{\text{c}}}={Q}_{{\text{s}}}\) = 50 Nm).

Case 1 and 2 are included to investigate the effect of the asymmetric loading on a tandem: i.e. the eccentric drive and timing chain tensions in combination with alternating left/right pedal forces. Case 3 allows comparison of forces on a tandem with those on a solo bicycle. Case 4 considers the much larger in-plane loading resulting from high-speed cornering in a velodrome. The effective 2g load is based on an upper limit for racing on a banked velodrome: a speed of ~ 18 m/s, turn radius ~ 20 m, lean angle (from vertical) ~ 60° [23, 24]. Riders are assumed in identical body positions to the base case but, due to high speed, contributing reduced torques. Aerodynamic drag dominates and there is no acceleration; however, the centre of aerodynamic pressure is assumed to be at the same height as the riders’ CoM and thus the equations are used unchanged.

2.4 Structural analysis of different frame types

FEA was used to determine the structural performance of four tandem frame topologies (Fig. 1). The goal is to determine whether the additional mass of lateral tubing in the double diamond, direct lateral and marathon frame designs provides a proportional increase in stiffness, where the scope is limited to equal tube sizes for each topology. The open frame was used as a base model with dimensions (Fig. 4b) carried over to the other three topologies. Main tubes have circular cross sections with diameters of 51.1 mm (bottom and down tubes), 38.5 mm (top tube) and 35 mm (seat and any lateral tubes). Chain and seat stays have radiused (R4 mm) rectangular profiles: 22.5 × 11.25 mm and 20.5 × 10.25 mm, respectively. Wall thickness is 2 mm for all tubes. A single material (aluminium alloy: E = 69 GPa, \(\nu\) = 0.33) was used for all models (note that, although absolute results will differ, the relative performance of the different topologies should be broadly similar for frames constructed from tubular steel or carbon fibre-reinforced plastic).

Linear elastic analysis was performed using Solidworks (Dassault Systémes). Each frame was meshed with solid parabolic tetrahedral elements (each 10 node with 16 Jacobian points); the use of a solid model attempts to model realistic weld fillets, see Fig. 5. Through a mesh convergence study on the open frame design, by increasing the number of elements progressively from 50,000 up to 9.3 million, it was determined that converged deflection results (< 0.1% change) could be obtained for a mesh with 3.4 million elements. All frames were then meshed at this resolution with elements of maximum size 1.5 mm (ensuring at least two elements across all tube walls). Combined meshing and analysis time were ~ 10 min on a 64 bit desktop PC with a 4 core Intel i7 3.4 GHz CPU and 64 GB of RAM.

3 Results

3.1 Validation of rider equilibrium

Published FE analyses of bicycles [e.g. 9–13] typically consider at least one load case representative of unseated starting or hill climbing. Although values of applied handlebar and pedal force boundary conditions are provided, no information is given on how to scale these forces for different rider mass or input torque; the works of Soden [8, 20] and Hull [15, 16] are the key references cited.

Equations (7–15) presented in this study provide a method for such scaling and may be partially validated by comparison with experimental measurements from these key references (Table 2). Soden and Adeyefa [20] measured pedal forces for starting on level ground with two subjects and provided CoM dimensions. Calculated pedal forces are in reasonable agreement with measurements (mean error ~ 0.1 mg). Stone and Hull [16] measured both handlebar and pedal forces for an unseated cyclist climbing a gradient. Unfortunately, no rider dimensions are provided and the vertical motion of the cyclist introduces additional uncertainty. Nevertheless, with CoM position estimated and the assumption of vertical equilibrium, the calculated values of all four rider forces are in very good agreement with the measurements (mean error ~ 0.02 mg).

Table 2 Comparison of calculated forces on a cyclist with literature measurements
Full size table

3.2 Forces

The key results for the base and comparison cases are given in Table 3: (i) vertical forces acting on the captain and stoker at handlebars and pedals, (ii) forces acting on the bottom bracket bearings. Forces applied to FEA models are equal and opposite reactions of these handlebar and bearing forces.

Table 3 Forces (as fractions of rider weight mg) on riders and bearings in tandem base and comparison cases
Full size table

3.3 Structural analysis of frame types

Figure 6 shows the deflected form of the open frame for the base (starting) load case with (a) the standard left-hand timing chain and (b) a right-hand timing chain. Deflections are magnified ten times. Twisting of the frame is the dominant deformation mode and this leads to large lateral (y) deflections (perpendicular to a plane through the rear wheel). Other deformation modes to note are bending of the bottom tube and deflection of the rear triangle, due to the eccentric loading of timing and drive chains, respectively. With a left-hand timing chain, these deformations cancel each other out to some extent (Fig. 6a), but with a right-hand timing chain they combine and the consequent lateral displacement is larger (Fig. 6b).

Fig. 6
figure 6

Deflected shape of open tandem frame under start load case for a conventional left-hand timing chain and b a right-hand timing chain (deflections amplified 10 times, superimposed on undeformed shape, contours of von Mises stress)

Full size image

The deflected forms of the other three tandem frame topologies (each with a left-hand timing chain) are similar to those in Fig. 6a and thus best compared numerically; Table 4 lists the key results for all four frame types.

Table 4 Key results of finite element analysis of tandem frame types
Full size table

4 Discussion

4.1 Forces

4.1.1 Base case

The captain and stoker are of identical stature and strength, and therefore the handlebar and pedal forces acting upon them are the same. The forces on each rider are given as proportions of body weight in mg in Table 3 and Fig. 7a. To apply the required torque, the cyclist is pushing down with ~ 2 mg (twice their body weight) on the leading pedal, pulling up on the trailing pedal with ~ 0.5 mg and also pulling up on the handlebars with a net force of ~ 0.6 mg. This net handlebar pull actually consists of a pull-up on one handlebar of ~ 1 mg and a push down on the other of ~ 0.4 mg. These magnitudes are in close agreement with those calculated by Soden and Adeyefa [20]. The bottom bracket bearing loads for the base case are large: the net loads in the stoker bearings are in excess of 8 kN.

Fig. 7
figure 7

Base case input dimensions (mm) and output rider forces (as proportions of rider weight mg), side and rear view, for: a base case, b 2g turn

Full size image

4.1.2 Right pedals forward

For both riders, pedal and handlebar forces are swapped left/right and reversed in magnitude compared to the base case, see Table 3. There is a consequent change in the z components of the bottom bracket forces (although not an exact swap for the stoker bottom bracket due to the z component of the unchanged drive chain tension).

4.1.3 Right-hand timing chain

Although a left-hand timing chain is the most common arrangement, it can be seen in Table 3 that a right-hand timing chain will significantly reduce the stoker bottom bracket loads. Because tensions in timing and drive chain are almost in balance, the horizontal (x) components of the bottom bracket forces are even lower than those for a solo bicycle. This reduction in bottom bracket forces will reduce bearing wear.

4.1.4 Solo bicycle

On the solo bicycle, the drive chain tension is half that of the tandem and this results in a small change to the z components of the bottom bracket forces. However, the absence of a timing chain makes the largest difference: the horizontal (x) components of the bottom bracket forces on the solo bicycle are approximately 2.5 and 8 times smaller than those for the tandem, on the right and left sides, respectively. The much higher loads on the tandem bottom bracket, compared to a solo bicycle, have implications for frame deflection and fatigue life of the bearings.

4.1.5 Tandem, 2g turn

Loads for a high-speed corner are shown in the last column in Table 3 and in Fig. 7b. The lower torque and the high centripetal loading mean that the rider now has a net push down on the handlebars of ~ 0.7 mg with the remaining net support of ~ 1.3 mg coming from the two pedal forces. In practice, a rider at such a high speed would usually be in a somewhat different position and on the bicycle saddle. Nevertheless, this load case represents the possibility of the rider attempting to further accelerate, out of the saddle, when at high speed.

4.2 Structural analysis of frame types

For all frames under the start load case, the lateral (y) deflection of the head tube is larger than the vertical (z) deflection of the bottom brackets (Table 4). The open frame, due to its lack of bracing, has the largest vertical deflection, but this is still only 0.5 mm compared to a lateral deflection of 9 mm. Nevertheless, because of this lower stiffness, we also consider the open frame’s deflection under the higher in-plane loading of the 2g turn (last column of Table 4). In fact, the vertical deflection for the open frame in the 2g turn load case is only 0.3 mm, although the rider weight is double the redistributed handlebar and pedal forces, due to the lower torque, also influence the vertical deflection. Twisting is reduced in the 2g turn and we therefore conclude that the start is the most significant load case for all the frames. For the open frame, analysis was also performed for a right-hand timing chain. Lateral deflection of the head tube (from the plane through the rear wheel) was 33.5 mm, almost four times greater than the base case (left-hand timing chain); compare Fig. 6a, b. The reason for this much larger lateral deflection is that the eccentric loadings of timing and drive chain tensions are now on the same side and the bottom tube therefore deflects in the same direction as the rear triangle. In the start load case, the applied x axis torque from each rider is 179 Nm. The longitudinal twist of the frame under these torques will be experienced by each rider as undesirable flexibility, manifested as vertical deflections when amplified by the width of the handlebar and pedal contact points (much larger than any vertical compression/extension of the frame). Finding the difference between the x axis rotation of the head tube and the captain’s bottom bracket allows the longitudinal twist stiffness of the frame for the captain to be calculated. The twist stiffness for the stoker is found from the difference in the x rotation of the captain’s seatpost (where the handlebars are assumed to be mounted) and the stoker’s bottom bracket. These handlebar-to-pedal twist stiffnesses are reported in Table 4. The direct lateral frame has the highest captain twist stiffness; the additional tubes intersecting with the captain’s seat tube reduce the bending deflection of that tube and consequently reduce the rotation of the bottom bracket. The marathon frame is less effective in this regard because the extra tubing has a longer span: it does not terminate at the stoker bottom bracket, but instead splits into an extra fork that continues to the rear axle. The double-diamond frame is only the third best for captain twist stiffness, but has the highest stoker twist stiffness. The additional tube mimics the down tube in providing a direct torsional load path between the handlebars and bottom bracket. Although the three alternative frame designs all provide more stiffness than the open frame, they all do so with a weight penalty. Taking the mean of the captain and stoker twist stiffness and normalising by mass provides a measure of the structural efficiency of the frames (Table 4). On this basis, the double-diamond frame is the best performing, narrowly ahead of the open frame. For the double-diamond frame, the additional tube provides a mean twist stiffness 15% higher than the open frame at a cost of only 12% extra mass. In contrast, the extra tubing on the direct lateral and marathon frames provides only 14% or 11% increase in mean twist stiffness whilst adding 20% or 25% to the frame mass, respectively.

5 Conclusions

This paper presents a method for estimating loads on a tandem frame based only on measured crank torques. Despite limiting assumptions regarding rider equilibrium and force distribution, the major twisting action forces are in reasonable agreement with literature measurements. It is shown that a standing start gives approximately the same vertical deflection as a 2g turn, but a lateral deflection five times higher. It is therefore concluded that a maximal standing start effort is the worst load case (at least for use on approximately level ground). For this load case, bottom bracket bearing loads on a tandem can be up to eight times higher than on a solo bicycle. Moving the timing chain to the right-hand side of the frame can significantly reduce these bearing loads for the stoker bottom bracket, but at the cost of much greater lateral deflection. Finite element analysis has been used to assess the flexibility of welded aluminium tandem frames with common tube dimensions, but different topologies. On a stiffness/weight basis, for twisting, the double diamond is the best of the common frame designs. However, it is only 2% superior to the open frame. Since an open frame should also be simpler to manufacture, and is probably superior aerodynamically, these advantages may ultimately make it the preferred design.