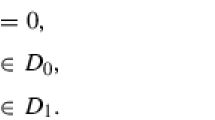Skip to main content
SpringerLink
Log in

On decompositions of permutation polynomials into quadratic and cubic power permutations

  • Published:
Cryptography and Communications Aims and scope Submit manuscript

Abstract

Decomposing permutation polynomials into power permutations of small algebraic facilitates the reduction of hardware area requirements when symmetric cryptographic algorithms are implemented with countermeasures to side channel attacks in mind. Our contribution in this work is twofold. Firstly, we determine such decompositions into power permutations of the field \({\mathbb F}_{2^{n}}\) of degree at most 2 for infinitely many odd n satisfying a specific property. Secondly, after improving the complexity of an existing algorithm, we use it to complete the list of known shortest decompositions of the inversion in \({\mathbb F}_{2^{n}}\) up to n = 32, and show that always considering degrees at most 3 can lead to shorter lengths or smaller area requirements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. https://oeis.org/A014657

References

  1. Carlet, C., Goubin, L., Prouff, E., Quisquater, M., Rivain, M.: Higher-order masking schemes for s-boxes. In: Proceedings of FSE, LNCS, vol. 7549, pp 366–384 (2012). https://doi.org/10.1007/978-3-642-34047-5_21

  2. Carlet, C., Prouff, E.: Polynomial evaluation and side channel analysis. In: The New Codebreakers, LNCS, vol. 9100, pp 315–341 (2016). https://doi.org/10.1007/978-3-662-49301-4_20

  3. Carlet, C., Prouff, E., Rivain, M., Roche, T.: Algebraic decomposition for probing security. In: Proceedings of CRYPTO, LNCS, vol. 9215, pp 742–763 (2015). https://doi.org/10.1007/978-3-662-47989-6_36

  4. Carlitz, L.: Permutations in a finite field. Proc. Amer. Math. Soc. 4, 538 (1953)

    Article  MATH  Google Scholar 

  5. Coron, J.S., Roy, A., Vivek, S.: Fast evaluation of polynomials over finite fields and application to side-channel countermeasures, vol. 8731, pp 170–187 (2014). https://doi.org/10.1007/978-3-662-44709-3_10

  6. Lidl, R., Niederreiter, H.: Finite fields. vol 20, Cambridge University press (1997)

  7. McEliece, R.: Crosscorrelation properties of m-sequences. In: Finite fields for computer scientists and engineers, vol. 23. https://doi.org/10.1007/978-1-4613-1983-2_11 (1987)

  8. Moree, P.: On the divisors of ak + bk. ACTA ARITHMETICA LXXX. 3, 197–212 (1997). https://doi.org/10.4064/aa-80-3-197-212

    Article  MATH  Google Scholar 

  9. Nikova, S., Nikov, V., Rijmen, V.: Decomposition of permutations in a finite field. Cryptogr. Commun. 11, 37–41 (2019). https://doi.org/10.1007/s12095-018-0317-2

    Article  MATH  Google Scholar 

  10. Nikova, S., Rechberger, C., Rijmen, V.: Threshold implementations against side-channel attacks and glitches. In: Proceedings of ICICS, LNCS, vol. 4307, pp 529–545 (2006). https://doi.org/10.1007/11935308_38

  11. Otal, K., Tekin, E.: Efficient generation of quadratic cyclotomic classes for shortest quadratic decompositions of polynomials. Cryptogr Commun (2021). https://doi.org/10.1007/s12095-021-00512-z

  12. Petrides, G.: On non-completeness in threshold implementations. In: Proceedings of ACM Workshop TIS@CCS 2019, pp 24–28 (2019). https://doi.org/10.1145/3338467.3358951

  13. Petrides, G.: A number theoretic view on binary shift registers. Cryptogr and Comm (2022). https://doi.org/10.1007/s12095-022-00562-x

  14. Roy, A., Vivek, S.: Analysis and improvement of the generic higher-order masking scheme of FSE 2012. In: Proceedings of CHES, LNCS, vol. 8086, pp 417–434 (2013). https://doi.org/10.1007/978-3-642-40349-1_24

  15. Ruskey, F., Sawada, J.: An efficient algorithm for generating necklaces with fixed density. SIAM J. Comput. 29(2), 671–684 (1999). https://doi.org/10.1137/S0097539798344112

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The author would like to express his appreciation towards the reviewers and the editor for comments that helped improve the manuscript.

Funding

Part of this work was supported by The Research Council of Norway under projects 247742/O70 and 314395 while the author was affiliated with the University of Bergen, Norway.

Author information

Authors and Affiliations

  1. Nicosia, Cyprus

    George Petrides

Authors
  1. George Petrides
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to George Petrides.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Petrides, G. On decompositions of permutation polynomials into quadratic and cubic power permutations. Cryptogr. Commun. 15, 199–207 (2023). https://doi.org/10.1007/s12095-022-00600-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12095-022-00600-8

Keywords

Search

Navigation