Bayesian-Weighted Triplet and Quartet Methods for Species Tree Inference

Abstract

Inference of the evolutionary histories of species, commonly represented by a species tree, is complicated by the divergent evolutionary history of different parts of the genome. Different loci on the genome can have different histories from the underlying species tree (and each other) due to processes such as incomplete lineage sorting (ILS), gene duplication and loss, and horizontal gene transfer. The multispecies coalescent is a commonly used model for performing inference on species and gene trees in the presence of ILS. This paper introduces Lily-T and Lily-Q, two new methods for species tree inference under the multispecies coalescent. We then compare them to two frequently used methods, SVDQuartets and ASTRAL, using simulated and empirical data. Both methods generally showed improvement over SVDQuartets, and Lily-Q was superior to Lily-T for most simulation settings. The comparison to ASTRAL was more mixed—Lily-Q tended to be better than ASTRAL when the length of recombination-free loci was short, when the coalescent population parameter $\theta$ was small, or when the internal branch lengths were longer.

Appendix

1.1 Calculation of $\varvec{\delta }|S$ for 4-Taxon Trees

From Chifman and Kubatko (2015), as in the 3-taxon case $P(\varvec{\delta }|(S,\varvec{\tau }))$ is the inner product $\mathbf{c }^{T}\mathbf{b }$ where $\mathbf{c }$ is a vector of constants times a function of $\varvec{\tau }$ that is of the form $e^{-a\tau _1-b\tau _2-g\tau _3}$.

1.1.1 Asymmetric Case

From (Chifman and Kubatko 2015) we have the following, converting to coalescent units from mutation units and using 4 characters $\{A,C,G,T\}$:

$$\begin{aligned} \delta _k|(s,\varvec{\tau })= & {} 1/256(c_0+c_1\frac{e^{-\alpha \theta \tau _1}}{(1+\alpha \theta )} +c_2\frac{e^{-\alpha \theta \tau _2}}{(1+\alpha \theta )} +c_3\frac{e^{-\alpha \theta (\tau _1/2+\tau _2)}}{(1+\alpha \theta )(1+2\alpha \theta )}\\&+c_4\frac{e^{-\alpha \theta \tau _3}}{(1+\alpha \theta )} \\&+c_5\frac{e^{-\alpha \theta (\tau _1/2+\tau _3)}}{(1+\alpha \theta )(1+2\alpha \theta )} +c_6\frac{e^{-\alpha \theta (\tau _1+\tau _3)}}{(1+\alpha \theta )^2} +c_7\frac{e^{-\alpha \theta (\tau _2/2+\tau _3)}}{(1+\alpha \theta )(1+2\alpha \theta )}\\&+c_8\frac{e^{-\alpha \theta (\tau _1/2+\tau _2/2+\tau _3)}}{(1+\alpha \theta )(1+2\alpha \theta )^2} +c_9\frac{e^{-\alpha \theta (\tau _2+\tau _3)-(\tau _2-\tau _1)}}{(1+\alpha \theta )^2(1+2\alpha \theta )^2(1+3\alpha \theta )} ) \end{aligned}$$

where the coefficients are given by Table 4.

Table 4 Coefficients for each site pattern probability—asymmetric

We have from the Yule model that $\tau _1 \sim Exp(4\beta )$, $(\tau _2-\tau _1) \sim Exp(3\beta )$, and $(\tau _3-\tau _2) \sim Exp(2\beta )$. Then:

$$\begin{aligned} f(\varvec{\tau })= (4\beta )e^{-4\beta \tau _1}(3\beta )e^{-3\beta (\tau _2-\tau _1)}(2\beta )e^{-2\beta (\tau _3-\tau _2)}=(24\beta ^3)e^{-\beta \tau _1-\beta \tau _2-2\beta \tau _3} \end{aligned}$$

Then, integrating over $f(\varvec{\tau })$ gives:

$$\begin{aligned}&\int _0^{\infty } \int _0^{\tau _3} \int _0^{\tau _2} e^{-a\tau _1-b\tau _2-g\tau _3} (24\beta ^3)e^{-\beta \tau _1-\beta \tau _2-2\beta \tau _3} \mathrm{d}\tau _1 \mathrm{d}\tau _2 \mathrm{d}\tau _3 \\&\quad =\int _0^{\infty }(24\beta ^3) e^{-\tau _3(c+2\beta )} \left( \int _0^{\tau _3}e^{-\tau _2(b+\beta )} \left( \int _0^{\tau _2} e^{-\tau _1(a+\beta )} \mathrm{d}\tau _1\right) \mathrm{d}\tau _2\right) \mathrm{d}\tau _3 \\&\quad =\frac{24\beta ^3}{a+\beta } \int _0^{\infty } e^{-\tau _3(c+2\beta )} \left( \int _0^{\tau _3}e^{-\tau _2(b+\beta )}\left( 1-e^{-\tau _2(a+\beta )}\right) \mathrm{d}\tau _2 \right) \mathrm{d}\tau _3 \\&\quad =\frac{24\beta ^3}{a+\beta }\int _0^{\infty } e^{-\tau _3(c+2\beta )}\left( \frac{1-e^{-\tau _3(b+\beta )}}{b+\beta }-\frac{1-e^{-\tau _3(a+b+2\beta )}}{a+b+2\beta }\right) \mathrm{d}\tau _3\\&\quad = \frac{24\beta ^3}{a+\beta }\left( \frac{1}{(c+\beta )(b+\beta )}-\frac{1}{(b+\beta )(b+c+3\beta )}-\frac{1}{(a+b+2\beta )(c+2\beta )}\right. \\&\left. \qquad +\frac{1}{(a+b+2\beta )(a+b+c+4\beta )}\right) \\&\quad =\frac{24\beta ^3}{(c+2\beta )(b+c+3\beta )(a+b+c+4\beta )} \end{aligned}$$

Applying this formula to each term above gives:

$$\begin{aligned} \delta _k|S= & {} \frac{1}{256}(c_0+c_1\frac{4\beta }{(1+\alpha \theta )(4\beta +\alpha \theta )}+c_2\frac{12\beta ^2}{(1+\alpha \theta )(3\beta +\alpha \theta )(4\beta +\alpha \theta )} \\&+c_3\frac{12\beta ^2}{(1+\alpha \theta )(2+\alpha \theta )(3\beta +\alpha \theta )(4\beta +3\alpha \theta /2)}\\&+c_4\frac{24\beta ^3}{(1+\alpha \theta )(2\beta +\alpha \theta )(3\beta +\alpha \theta )(4\beta +\alpha \theta )} \\&+c_5\frac{24\beta ^3}{(1+\alpha \theta )(2+\alpha \theta )(2\beta +\alpha \theta )(3\beta +\alpha \theta )(4\beta +3\alpha \theta /2)}\\&+c_6\frac{24\beta ^3}{(1+\alpha \theta )^2(2\beta +\alpha \theta )(3\beta +\alpha \theta )(4\beta +2\alpha \theta )} \\&+c_7\frac{24\beta ^3}{(1+\alpha \theta )(2+\alpha \theta )(2\beta +\alpha \theta )(3\beta +3\alpha \theta /2)(4\beta +3\alpha \theta /2)} \\&+c_8\frac{24\beta ^3}{(1+\alpha \theta )(2+\alpha \theta )^2(2\beta +\alpha \theta )(3\beta +3\alpha \theta /2)(4\beta +2\alpha \theta )} \\&+c_9\frac{24\beta ^3}{(1+\alpha \theta )^2(2+\alpha \theta )^2(3+\alpha \theta )(2\beta +\alpha \theta )(3\beta +2\alpha \theta +1)(4\beta +2\alpha \theta )} ) \end{aligned}$$

1.1.2 Symmetric Case

From (Chifman and Kubatko 2015) we have the following, converting to coalescent units from mutation units and using 4 characters $\{A,C,G,T\}$:

$$\begin{aligned} \delta _k= & {} 1/256(c_0+c_1\frac{e^{-\alpha \theta \tau _1}}{(1+\alpha \theta )} +c_2\frac{e^{-\alpha \theta \tau _2}}{(1+\alpha \theta )} +c_3\frac{e^{-\alpha \theta (\tau _1/2+\tau _2)}}{(1+\alpha \theta )^2} +c_4\frac{e^{-\alpha \theta \tau _3}}{(1+\alpha \theta )}\\&+c_5\frac{e^{-\alpha \theta (\tau _1/2+\tau _3)}}{(1+\alpha \theta )(1+2\alpha \theta )} +c_6\frac{e^{-\alpha \theta (\tau _2/2+\tau _3)}}{(1+\alpha \theta )(1+2\alpha \theta )} +c_7\frac{e^{-\alpha \theta (\tau _1/2+\tau _2/2+\tau _3)}}{(1+\alpha \theta )(1+2\alpha \theta )^2}\\&+c_8\frac{e^{-2\alpha \theta \tau _3-(\tau _3-\tau _1)-(\tau _3-\tau _2)}}{(1+\alpha \theta )^2(1+2\alpha \theta )^2(1+3\alpha \theta )} ) \end{aligned}$$

where the coefficients are given by Table 5.

Table 5 Coefficients for each site pattern probability—symmetric

The prior differs from the asymmetric case in that $\tau _1<\tau _2$ and $\tau _2<\tau _1$ occurs with equal probability. The form of the integrals are the same in either case, just substituting the coefficients in front of $\tau _1$ and $\tau _2$. As a result, integrating over the prior gives (where the only difference between the terms is the a or b in the middle factor of the denominator):

$$\begin{aligned} \frac{12\beta ^3}{(c+2\beta )(b+c+3\beta )(a+b+c+4\beta )}+\frac{12\beta ^3}{(c+2\beta )(a+c+3\beta )(a+b+c+4\beta )} \end{aligned}$$

Applying this formula to each term above gives:

$$\begin{aligned} \delta _k|S= & {} \frac{1}{256}\bigg (c_0+\frac{c_1+c_2}{1+\alpha \theta }(\frac{2\beta }{4\beta +\alpha \theta }+\frac{6\beta ^2}{(3\beta +\alpha \theta )(4\beta +\alpha \theta )})\\&+c_3\frac{12\beta ^2}{(1+\alpha \theta )^2(3\beta +\alpha \theta )(4\beta +2\alpha \theta )} \\&+c_4\frac{24\beta ^3}{(1+\alpha \theta )(2\beta +\alpha \theta )(3\beta +\alpha \theta )(4\beta +\alpha \theta )} \\&+\frac{(c_5+c_6)12\beta ^2}{(1+\alpha \theta )(2+\alpha \theta )}(\frac{1}{(2\beta +\alpha \theta )(3\beta +\alpha \theta )(4\beta +3\alpha \theta /2)}\\&+\frac{1}{(2\beta +\alpha \theta )(3\beta +3\alpha \theta /2)(4\beta +3\alpha \theta /2)}) \\&+c_7\frac{24\beta ^3}{(1+\alpha \theta )(2+\alpha \theta )^2(2\beta +\alpha \theta )(3\beta +3\alpha \theta /2)(4\beta +2\alpha \theta )} \\&+c_8\frac{24\beta ^3}{(1+\alpha \theta )^2(2+\alpha \theta )^2(3+\alpha \theta )(2\beta +\alpha \theta +2)(3\beta +2\alpha \theta +1)(4\beta +2\alpha \theta )} \bigg ) \end{aligned}$$

1.2 Calculation of $\varvec{\delta }|(S,\varvec{\tau }))$ for 3-Taxon Trees

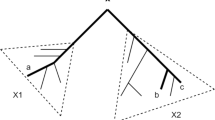
The fifteen site pattern probabilities shown above for the 4-taxon case can be mapped down to the five site patterns for three taxa by summing over the fourth taxon we are not interested in. Any of the four taxa can be used, however, we found it simplest to marginalize over the outgroup of the asymmetric tree (see Fig. 3) to get the following relationships (dropping the conditioning on $(S, \varvec{\tau })$ for clarity):

$$\begin{aligned}&p_0=\delta _{XXX}=\delta _{XXXX}+3\delta _{YXXX} \\&p_1=\delta _{YXX}=\delta _{XYXX}+\delta _{XXYY}+2\delta _{YZXX} \\&p_2=\delta _{XXY}=\delta _{XYX}=\delta _{XXXY}+\delta _{XYYX}+2\delta _{YXXZ}=\delta _{XXYX}+\delta _{XYXY}+2\delta _{YXZX} \\&p_3=\delta _{XYZ}=\delta _{XXYZ}+\delta _{XYXZ}+\delta _{XYZX}+\delta _{XYZW} \end{aligned}$$

These probabilities take the form:

$$\begin{aligned} \left\{ \begin{aligned}&p_0=c_0+3c_1+6c_2+12c_3\\&p_1=c_0+3c_1-2c_2-4c_3\\&p_2=c_0-c_1+2c_2-4c_3\\&p_3=c_0-c_1-2c_2+4c_3 \end{aligned} \right. \end{aligned}$$

(6)

where (measuring $\tau _1$ and $\tau _2$ in coalescent units):

$$\begin{aligned} \left\{ \begin{aligned}&c_0=1/64\\&c_1=\frac{e^{-\tau _1\alpha \theta }}{64(1+\alpha \theta )}\\&c_2=\frac{e^{-\tau _2\alpha \theta }}{64(1+\alpha \theta }\\&c_3=\frac{e^{-\tau _1\alpha \theta /2}e^{-\tau _2\alpha \theta }}{64(1+2\alpha \theta )(1+\alpha \theta )} \end{aligned} \right. \end{aligned}$$

(7)

It is easily verified that:

$$\begin{aligned} 4p_0+12p_1+24p_2+24p_3=1 \end{aligned}$$

(8)

The coefficients in Eq. 8 arise as follows. X can represent any of A, C, G, or T. Y can represent any of the remaining three characters, and Z any of the remaining two. Finally, the coefficient of $p_2$ is doubled to account for both $\delta _{XYX}$ and $\delta _{XXY}$.

1.3 Calculation of $\varvec{\delta }|S$ for 3-Taxon Trees

One can see from Eq. 6 that $\delta _k|(S,\varvec{\tau })$ is a linear combination of terms, so $\delta _k|S$ is also linear combination of terms. Given $\tau _1 \sim Exp(3\beta )$ and $(\tau _2-\tau _1) \sim Exp(2\beta )$, the prior is:

$$\begin{aligned} f(\varvec{\tau }|\beta ) = 3\beta e^{-3\beta \tau _1}2\beta e^{-2\beta (\tau _2-\tau _1)}=6\beta ^2e^{-\beta \tau _1-2\beta \tau _2} \end{aligned}$$

Then to integrate over $f(\varvec{\tau }|\beta )$, each term has the form:

$$\begin{aligned}&\int _0^{\infty } \int _0^{\tau _2} e^{-a\tau _1}e^{-b\tau _2}6\beta ^2e^{-\beta \tau _1-2\beta \tau _2} \mathrm{d}\tau _1 \mathrm{d}\tau _2 \\&=\int _0^{\infty }6\beta ^2 e^{-\tau _2(b+2\beta ))}(\int _0^{\tau _2}e^{-\tau _1(a+\beta ))} \mathrm{d}\tau _1) \mathrm{d}\tau _2 \\&=\frac{6\beta ^2}{a+\beta }\int _0^{\infty }6\beta ^2 e^{-\tau _2(b+2\beta ))}(1-e^{-\tau _2(a+\beta ))}) \mathrm{d}\tau _2 \\&=\frac{6\beta ^2}{a+\beta }(\frac{1}{b+2\beta }-\frac{1}{a+b+2\beta }) \\&= \frac{6\beta ^2}{(b+2\beta )(a+b+3\beta )} \end{aligned}$$

Taken together, $\delta _k|S$ has the linear form of Eq. 6 with the following terms replacing those of Eq. 7:

$$\begin{aligned} \left\{ \begin{aligned}&c_0=1/64\\&c_1=\frac{3\beta }{(1+\alpha \theta )(3\beta +\alpha \theta )}\\&c_2=\frac{6\beta ^2}{(1+\alpha \theta )(2\beta +\alpha \theta )(3\beta +\alpha \theta )}\\&c_3=\frac{3\beta }{(1+\alpha \theta )(1+2\alpha \theta )(2\beta +\alpha \theta )(3\beta +3\alpha \theta /2)} \end{aligned} \right. \end{aligned}$$

(9)

where $\alpha =4/3$ from the JC69 model. Comparison to the results in the supplementary material reveals the computational advantages of the Yule model approach.

1.4 Proof of Theorem 1

Proof

Without loss of generality, let $S_0=(a,(b,c))$ be the true tree and $\varvec{\tau }_0$ be the true value of $\varvec{\tau }$. We want to show that $\forall \epsilon>0 \, \, \exists J_0 : \forall J>J_0 \, \, P({\hat{S}}=S)>1-\epsilon$. First, note that for all values of $(\varvec{\tau }, \theta )$, we have $\delta _{XXY}=\delta _{XYX}$.

Second, we note using the results of Eq. 6

$$\begin{aligned} \delta _{YXX}|((a,(b,c)),\varvec{\tau }) > \delta _{XYX}|((a,(b,c)),\varvec{\tau }) \end{aligned}$$

(10)

$$\begin{aligned}&\leftrightarrow c_0+3c_1-2c_2-4c_3> c_0-c_1+2c_2-4c_3 \\&\leftrightarrow \frac{e^{-\alpha \tau _1\theta }}{64(1+\alpha \theta )}=c1>c2=\frac{e^{-\alpha \tau _2\theta }}{64(1+\alpha \theta )} \\&\leftrightarrow \tau _1<\tau _2 \end{aligned}$$

which holds w.p.1 by assumption.

Next, note

$$\begin{aligned}&\int _{\varvec{\tau }}\delta _{YXX}|((a,(b,c)),\varvec{\tau })f(\varvec{\tau })\mathrm{d}(\varvec{\tau })=\delta _{YXX}|(a,(b,c)) \\&> \delta _{XYX}|(a,(b,c))=\int _{\varvec{\tau }}\delta _{XYX}|((a,(b,c)),\varvec{\tau })f(\varvec{\tau })\mathrm{d}(\varvec{\tau }) \end{aligned}$$

by properties of expectations from Eq. 10 and since $f(\varvec{\tau })>0$ a.e. under the prior.

Since each topology (a, (b, c)), (b, (a, c)), and (c, (a, b)) has a prior probability of 1/3, the maximum posterior topology will be the maximum likelihood topology. Recall from Sect. 2.4 that we can permute any site pattern probability given one topology to find a site pattern probability given another topology—e.g., $\delta _{YXX}|(a,(b,c))=\delta _{XYX}|(b,(a,c))$. So, the likelihood of trees (a, (b, c)) and (b, (a, c)) given the data are:

$$\begin{aligned} L((a,(b,c))|{\varvec{d}})= & {} c_{{\varvec{d}}} (p_{xxx})^{d_{xxx}}(p_{xxy})^{d_{xxy}}(p_{xyx})^{d_{xyx}}(p_{yxx})^{d_{yxx}}(p_{xyz})^{d_{xyz}} \\ L((b,(a,c))|{\varvec{d}})= & {} c_{{\varvec{d}}} (p_{xxx})^{d_{xxx}}(p_{xxy})^{d_{xxy}}(p_{xyx})^{d_{yxx}}(p_{yxx})^{d_{xyx}}(p_{xyz})^{d_{xyz}} \end{aligned}$$

By cancelling terms in common, one can see that the likelihood ratio comes down to permuting the number of sites that follow the XYX and YXX patterns:

$$\begin{aligned} \frac{L((a,(b,c))|{\varvec{d}})}{L((b,(a,c))|{\varvec{d}})}= (p_{xyx})^{d_{xyx}-d_{yxx}}(p_{yxx})^{d_{yxx}-d_{xyx}} \end{aligned}$$

Together $p_{yxx}>p_{xyx}$ and $d_{yxx}>d_{xyx}$ imply that $\frac{L((a,(b,c))|{\varvec{d}})}{L((b,(a,c))|{\varvec{d}})}>1$, which implies that ${\hat{S}}=S$. As we have shown that $p_{yxx}>p_{xyx}$, it is sufficient to show that $\frac{d_{yxx}}{J} \rightarrow p_{yxx}$ and $\frac{d_{xyx}}{J} \rightarrow p_{xyx}$ for sufficiently large number of sites.

Let $p_{yxx,0}=\delta _{yxx}|((a,(b,c)),\varvec{\tau }_0)$ and $p_{xyx,0}=\delta _{xyx}|((a,(b,c)),\varvec{\tau }_0)$. From the SLLN, we have

$$\begin{aligned}&\forall \epsilon _1,\delta _1>0 \, \, \exists J_1 : \forall J>J_1 \, \, P(\frac{d_{yxx}}{J}>p_{yxx,0}-\delta _1)>1-\epsilon _1 \\&\forall \epsilon _2,\delta _2>0 \, \, \exists J_2 : \forall J>J_2 \, \, P(\frac{d_{xyx}}{J}<p_{xyx,0}+\delta _2)>1-\epsilon _2 \end{aligned}$$

Choose $\delta _1,\delta _2$ such that $\delta _1+\delta _2<p_{yxx,0}-p_{xyx,0}$, $\epsilon _1=\epsilon _2=\epsilon /2$, and $J_0=max\{J_1,J_2\}$ by applying the Bonferroni inequality we have that $P(\frac{d_yxx}{J}>p_{yxx,0}-\delta _1, p_{xyx,0}+\delta _2>\frac{d_{xyx}}{J})>1-\epsilon$ and the result holds.

$\square$