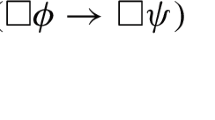Abstract
We propose a novel, ontological approach to studying mathematical propositions and proofs. By “ontological approach” we refer to the study of the categories of beings or concepts that, in their practice, mathematicians isolate as fruitful for the advancement of their scientific activity (like discovering and proving theorems, formulating conjectures, and providing explanations). We do so by developing what we call a “formal ontology” of proofs using semantic modeling tools (like RDF and OWL) developed by the computer science community. In this article, (i) we describe this new approach and, (ii) to provide an example, we apply it to the problem of the identity of proofs. We also describe open issues and further applications of this approach (for example, the study of purity of methods). We lay some foundations to investigate rigorously and at large scale intellectual moves and attitudes that underpin the advancement of mathematics through cognitive means (carving out investigationally valuable concepts and techniques) and social means (like communication, collaboration, revision, and criticism of specific categories, inferential patterns, and levels of analysis). Our approach complements other types of analysis of proofs such as reconstruction in a deductive system and examination through a proof-assistant.



Similar content being viewed by others
Notes
See, e.g., Arp et al. (2015): “[An ontology is] a representational artifact, comprising a taxonomy as proper part, whose representations are intended to designate some combination of universals, defined classes, and certain relations between them” (p. 1).
We view such components (conceptual choices, social standards, etc.) as essential to the production of mathematical knowledge and requiring careful analysis. Following a minority tradition in the philosophy of mathematics represented by works like Ernest (1998), Hersh and Davis (1981), and Cole (2013), we concentrate on some of these social aspects by providing new tools to study them.
One can access its latest release at the following internet address: http://www.ontobee.org/ontology/go.
To use an imperfect analogy, although one may reduce organisms to combinations of sub-atomic particles, doing so would usually be uninformative when one engages in biological investigations. The analogy is imperfect in the sense that, here, we neither claim nor deny that mathematical objects are ultimately just sets, objects of a category, or whatever other unifying type one may suggest.
SAT-solvers and SMT-solvers are examples of automated provers. With some limitations concerning the complexity of formulas, SAT-solvers check whether a set of propositional formulas is satisfiable (and, therefore, can also judge whether a given formula follows from a finite set of formulas). SMT-solvers check whether a set of formulas is satisfiable modulo a theory, e.g. whether a set of inequalities is satisfiable in the theory of the integers. An example of SAT-solver and SMT-solver is Z3, developed by Microsoft Research.
Like, for example, those focused on deduction like Isabelle/HOL, Coq, and Lean and those relying on machine learning. We will say more below.
Concerning this point, however, we note that researchers used the deductive capacities of ontologies to make interesting discoveries in non-mathematical domains. For example, (Wolstencroft et al. 2007) describes the use of OWL to discover a new protein.
In Beeson et al. (2019), Beeson and his collaborators declare: “Our aim was to remove every flaw from Euclid’s axioms, definitions, postulates, and common notions, and give formal proofs of all the propositions in Book I” (p. 246).
See Beeson et al. (2019) pp. 248–255).
For example, after reformulating Euclid’s proof of proposition I.1 in their framework, Beeson and collaborators show that the three vertices of the constructed figure are not collinear (and, therefore, the figure is indeed a triangle). Cf. Beeson et al. (2019, pp. 247–248).
In Sect. 4, we say more concerning how to select the appropriate level of analysis.
We do not claim that proof-assistants cannot be useful to study philosophical, historical, sociological, or psychological questions concerning the production or communication of mathematics. We also do not claim that, with some effort, one could not carry out the analysis that we exemplify in the rest of this paper using proof-assistants. We only say that, by design, ontologies are sometimes better suited to some investigations concerning mathematics than proof-assistants.
To conclude this paragraph, we remark again that the comparison between proof-assistants and ontologies deserves a fuller discussion. One ought to consider various approaches to validating, constructing, completing, or finding a proof, including newer approaches based on machine learning and natural language processing. Moreover, one ought to consider not only the alternative uses of proof-assistants (in a broad sense) and ontologies but also the possibility of their integration (for example, using simultaneously natural language processing to study vast mathematical corpora and ontologies to provide a schema to classify objects and procedures that are so detected). We leave a fuller discussion to another occasion.
See Dosen (2003) for a survey.
A finitistic reformulation of (S1) is the following: whenever p and q are natural numbers, it is not the case that \(p^2=2q^2\).
For example, when an author refers to segments, should we interpret segments as sets of points, mereological sums of points, or else? Should we take points to be tuples of real numbers (thus committing ourselves to numbers, sets, and cartesian products among other things)? Should we stick to the author’s original definition (if given at all) even if later generations of mathematicians did not consider it rigorous or “the right” one?
The noetic challenge deserves a fuller treatment in another paper. Here, we sidestep it merely for reasons of space. Such a strategy to sidestep the noetic challenge does not assume that, given an interpreted sentence, it is always possible (with reasonable, albeit here unspecified, resources) to extract its idea or provide a standard formulation of that idea. Similarly, extending the discussion from a single sentence to a list of sentences (which we also call a piece of text), we do not assume that there is something deserving to be called the main or core idea of that piece of text and that (given some resources) it is always possible to extract that idea or provide a standard formulation of it. We simply want to notice (and, given the focus of this paper, swiftly put aside) the following issue: often mathematicians refer to results (here we include both theorems and proofs) by phrases like “the irrationality of \(\sqrt{2}\)” (possibly, like in Gowers (2007), to refer to some or all statements (S1)-(S4) or to other formulations taken to express that fact) or “Euclid’s proof of the infinitude of prime numbers” (possibly to refer exactly to Euclid IX.20 or to some modern proof taken to rely on the same strategy). Such a linguistic fact witnesses the existence of the noetic challenge: mathematicians regard different statements or pieces of text to possibly express “the same idea” at some informative level of analysis and differ in details that, in a given context, are secondary. For example, most of the debate in Gowers (2007) holds regardless of whether the statement under discussion is (S1), (S2), or (S3) (or another one yet). In this paper, we take the pragmatic step of avoiding the noetic challenge by simply providing a specific statement and two specific proofs regardless of variants that, in the sense of this footnote, one could regard as expressing the same ideas. In this sense, sidestepping the noetic challenge does not dissolve or trivialize (PIP). In particular, even if it were possible to decide convincingly when two proofs express the same idea (at some appropriate level of analysis), we do not think it would follow that the two proofs rely on or presuppose the same ontology. We do not even claim that (PIP) can have only one solution. On the contrary, we think it is likely that, in this context, “identity” can be understood in many (legitimate and informative) ways. So, while “expressing the same idea” (if made precise) could be one solution to (PIP), it would still be possible to discuss identity concerning the ontology that proofs presuppose in the sense that we discuss below.
For example, if a statement refers to the set of natural numbers and there is no indication to the contrary, we count this as a reason to define such a set as it is typically defined in current mathematics (thus including 0 and being an actually infinite set).
For example, if, at the sentential level, a statement quantifies only over \(\mathbb {N}\), we take this to be a reason to count \(\mathbb {N}\) among the objects to which the statement is committed but, unless there is a clear indication to the contrary, we take that statement to be committed neither to the existence of \(\mathcal {P}(\mathbb {N})\) nor to von Neumann or Zermelo finite ordinals.
For example, Euclid talks about points in a plane and, often, we now represent such points as tuples in \(\mathbb {R}^2\). However, the fact that Euclid knew nothing about this representational apparatus counts as a reason to think that his formulation is not committed to \(\mathbb {R}^2\) and is also not committed to specific tuples of numbers.
Therefore, here, we take diagrams to have a purely cognitive role (i.e., for example, to facilitate devising or understanding a proof) and not a semantic one (i.e. they do not indicate any ontological commitment). We do so simply for convenience without implying anything about the nature(s) of diagrams and their role(s) in proofs.
Against the background of intuitionistic sentential logic [in the sense of Heyting (1971) ch. VII], LEM holds if and only if reductio is a valid inferential schema.
For Heyting, metaphysical neutrality consists in avoiding committing to any proposition or inferential schema that is justified only by the acceptance or rejection of the claim that there are “mathematical things existing independently of our knowledge” (Heyting 1971, ch. I p. 3).
Besides extra-mathematical considerations like the ones above, proofs by reductio pose a different challenge: do they commit one to the existence of impossible objects? The standard answer is no. Indeed the goal of a proof by reductio (as one typically understands it) is to show that something does not exist. The discussion of the ontological commitments of proofs by reductio and how to discern them systematically is important, but we will not deal with this issue here.
Heinrich Weber reports that Kronecker said: “Die ganzen Zahlen hat der liebe Gott gemacht” (Weber 1891, p. 19).
For a partially comparable emphasis on the structure of a proof in the context of formal representations of proofs, cf. the notion of hierarchical proof in Denney et al. (2006).
For this approach, proof-techniques are tree-types. A proof uses a specific proof-technique if it contains a sub-tree that instantiates that technique.
We define the notion of ontological commitment in Sect. 8.
To expand a bit, we found that OWL 2 provided us with the appropriate tools to study the proofs presented in Sect. 7. We are inclined to think that different projects concerning the ontological analysis of proofs may require different formal languages (with different expressiveness or different ductility or appropriateness of the elements and tools that they provide). Anyway, we do not discuss this issue here. A related issue, which we will also put aside after this brief mention, is whether different languages or logics have ontological commitments. The point is that the notion of “ontological commitment” is ambiguous. In the sense defined in Sect. 9, no sentence with only logical symbols (including equality) has an ontological commitment. In this sense, although \(\exists x\ x=x\) is a logical truth in classical first-order logic, it has no ontological commitment in the sense that we study here. We leave a fuller treatment of different notions of ontological commitment and what they reveal about different languages and logics to another paper.
A related worry concerning the use of OWL 2 is that, in this language and with the given semantics, one can express only first-order arguments. However, as we explained in Sect. 3.2, we are not trying to build an automated reasoner or proof-assistant and the expressive power of OWL 2 is enough for our analysis in Sects. 7 to 10. Therefore, such a limitation is not a problem for us, at least on this occasion. However, we do not exclude that, in some cases, the ontological analysis of proofs would be better developed in a higher-order language (like Cyc, for example).
See the following internet address: https://github.com/Mttbnchtt/ontology-and-proofs.
We do not claim that the categories that we adopt are sufficient or correct to meaningfully describe, not even at a general and domain-independent level, every important feature of theorems and proofs. We also make some simplifications. For example, here we classify definitions and axioms as claims but we do not exclude that, in further iterations, we may distinguish definitions and axioms from claims. We simply notice that the upper ontology that we present now has served us well in the cases that we studied and we leave the possibility of revising it open.
Besides sidestepping the issue concerning axioms discussed in footnote 32, here we also do not consider the question of whether axioms are propositions (or express a proposition) as opposed to propositional functions (Whitehead 1906, p. 2), uninterpreted formulas (Veblen and Young 1910, pp. 1–2), or hypotheses (Bernays 1922, p. 96). Such different notions of what axioms are are relevant to deciding whether axioms are claims and, more in general, to the construction of an upper ontology. However, the discussion of the nature(s) of axioms requires another paper. For now, classifying axioms as claims is enough.
Similarly to what we did in footnote 33 concerning axioms, here we also leave aside several questions concerning the nature(s) of proof steps, like whether they are (or express) propositions or are purely formal strings.
A binary relation < is a strict order on a set S if and only if it is irreflexive, asymmetric, and transitive on S, i.e., for every x, y, \(z \in S\), \(\lnot (x < x)\), \([x< y \rightarrow \lnot (y < x) ]\), and \([(x< y \wedge y< z) \rightarrow x < z]\).
Postulate 2: “And [let it have been granted] to produce a finite straight line (i.e. a segment) in a straight line continuously”.
Proposition I.16: “In every triangle, having extended one of the sides, the exterior angle is greater than each of the interior and opposite angles”.
Proposition I.13: “If a straight line put on a straight line produces angles, it produces either two right angles or [two angles] equal to two right angles”.
See Euclid I.17, slightly abridged, our translation.
Proclus In primum Euclidis [from the modern critical edition Proclus (1873, 311 17-21)], our translation.
One could develop Proclus’ observation to provide an ontological criterion to study what, in recent years, scholars have called the purity of proofs. This is an interesting development that, however, we will explore on another occasion. See also (Q1) in Sect. 11.
Postulate 1: “Let it have been granted to draw a straight line from every point to every point”.
Proclus (1873, 312.1-14), our translation.
One may think that also the first statement refers to a construction, i.e. the construction of a triangle. This is possible, although here we prefer to stick more closely to the superficial form of the statement. Nothing in this paper depends on whether we chose the first or the latter solution.
One may take such statements as referring to an agent that either provides, constructs, or manipulates some objects. One could add such an agent to the ontology and specify what it does: which objects (if any) it takes as input, which operations it carries out, and what the output is. Such an agential view of mathematics is interesting. For example, Brouwer speaks of the creating subject that constructs mathematical objects (e.g., Brouwer 1949, p. 491). Others have applied notions of agency to discuss algebra, computability, set-theory, and other mathematical subjects. However, here we stick to objects that are mathematical in a stricter sense.
By “object”, here we refer to an individual that belongs to one of the four classes mentioned in Sect. 8.1: angle, point, segment, and triangle.
For example, a new triangle in the step “let ABC be a triangle”.
For example, a new segment in the steps “let \(\overline{BC}\) be produced to D” (which entails the existence of the segment \(\overline{BD}\)) and “let A be joined to D” (which entails the existence of the segment \(\overline{AD}\)).
Though we do not present it as a general criterion, in this proof the ampliative steps are exactly those steps \(s-p-o\) where p is either (i) a relation referring to a construction (“producedTo” or “joinedTo”) or (ii) the is-a relation when used in a leaf of the graph representing the dependency of a step to others in the proof (when the is-a relation is used in non-leaf steps, it belongs to an informative step).
In footnote 45, we referred to the agential view of mathematics when discussing the notion of ampliative step. According to such a view, as we said, one sees some steps in a proof as instructing an agent to carry out some actions. It is important to notice that such actions may appear in what we here call informative steps. For example, one may consider noticing that something is the case as an action. However, even if one has a narrower notion of action, a step like “select a point on \(\overline{BC}\)” is an informative step in our sense, although such a selection still plausibly counts as an action. Such a step is informative in our sense because the point that the agent ends up selecting is a part of \(\overline{BC}\) (at least it is so once the agent has singled it out as a point on \(\overline{BC}\)).
Furthermore, (1) for reasons of purity that we do not discuss here but to which we alluded in footnote 41, Proclus argues that his proof is superior.
For example, on one level, one can observe that the so-called First Isomorphism Theorem for groups (if G and H are groups and \(f:G\rightarrow H\) is a homomorphism where \(K := \{a \in G: f(a) = 1\}\), then the image of f is isomorphic to the quotient group G/K) and the First Isomorphism theorem for rings (if R and S are rings and \(f:R\rightarrow S\) is a homomorphism where \(K := \{a \in R: f(a) = 0\}\), then the image of f is isomorphic to the quotient ring R/K) rely on the same strategy and their proofs, are, in this sense, the same. In fact, both theorems and proofs are special cases of what Burris and Sankappanavar call the Homomorphism Theorem (see Burris and Hanamantagouda (2012) theorem 6.12 p. 46). However, on another level, the two theorems are distinct because they refer to different objects (groups and rings, respectively) and, if, for some reason, one accepts groups but rejects rings, that person would believe the first theorem but not the second one.
See Sect. 5.1 for an explanation of the notion of triple.
These are properties that relate an individual to a piece of data, like hasWeight in the triple “John hasWeight 70” (where the unit of measure, in this case kilograms, is specified separately). In our ontology concerning Euclid’s and Proclus’ we do not use properties of this type. However, they may be useful in some contexts.
These are properties relating an individual to an individual, like producedTo in the triple “segment_BC producedTo point_D”. We use properties of this type in our ontology.
An annotation property links any resource (a class, an individual, or another property) to a human-readable note. We will ignore them in what follows.
‘ In this paper, we always take a first-order language to include equality among the logical constants.
The document (Bechhofer et al. 2004) defines what counts as a class description for a class. Avoiding technicalities, a class description is the definition of a class by one of the following means: (i) a name for C together with the statement that C is a class, (ii) a statement that C is the class of given individuals enumerated by their names, (iii) a statement that C is either the union, intersection, or complement of other classes described (as classes) in \(\mathscr {O}\), (iv) a statement that C contains exactly the elements that have specific values or a specific number of values for a given property (for example, the class of exactly those individuals that play basketball).
The logical consequence relation to which the symbol \(\models\) refer is classical.
The gist of this definition is that an informative property P can appear in \(\varphi (x)\) only with names with which it is used either in \(\mathscr {O}\) or in formulas that follow logically from \(\mathscr {O}\). Besides formulas appearing in \(\mathscr {O}\), we include formulas that follow from \(\mathscr {O}\) on the basis that everything that follows logically from the statements to which one is committed counts toward the determination of the types of objects (i.e. the ontological commitments) that a rational agent ought to accept. This condition avoids the counter-intuitive result that, for example, two direct (i.e. not using reduction ad absurdum) proofs \(P_1\) and \(P_2\) are deemed distinct simply because the only relation that \(P_1\) uses is a strict linear ordering and the only relation that \(P_2\) uses is a partial ordering even though one can define each ordering in terms of the other.
This has the welcomed consequence that impossible classes defined in a proof by contradiction are not ontological commitments of that proof. However, our definition of ontological commitment undergenerates when applied to a proof by contradiction if there is no criterion to distinguish the classes that are defined precisely to show that they are impossible from the others. Such a criterion would likely involve distinguishing between an ontological resource that is given and an ontological resource (later shown to be impossible) that is only assumed to be given. Such a refinement does not affect our analysis of Euclid’s and Proclus’ proofs and we leave it for another occasion.
We do not develop here such a notion of intellectual “fit”. We simply refer to considerations such as those developed in Feferman (2009, pp. 8–9).
There are legitimate doubts concerning the attribution of the definitions in book I of the Elements to Euclid. See Russo (1998).
For example, what if one sees I.16 and I.17 as a single proposition as, in Proclus (1873, 307 1-12), Proclus says some have done?
As we noted in footnote 41, one could interpret Proclus’ observation (1) also as showing concern for the purity of methods and suggesting to analyze such a notion comparing the ontological commitments of a proof with the ontological commitments of the statement that it establishes.
Dualization is the phenomenon by which two concepts, for example, point and line in projective geometry, can be replaced one for the other in a proposition without altering the truth value of that proposition. So, for example, given the proposition ‘any two distinct points of a plane are on one and only one line’, one can, by mechanical replacement, obtain ‘any two distinct lines of a plane are on one and only one point’.
For an example, see Simon and Hayes (1977).
In Greeno (1983), the cognitive psychologist James G. Greeno used the term ‘ontology’ explicitly and argued that different ontologies influence an agent’s ability to solve a problem.
References
Arp R, Smith B, Spear AD (2015) Building ontologies with Basic Formal Ontology. The MIT Press, Cambridge
Bechhofer S et al (2004) OWL Web Ontology Language Reference. https://www.w3.org/TR/owl-ref/
Beeson M, Narboux J, Wiedijk F (2019) Proof-checking Euclid. Ann Math Artif Intell 85(2–4):213–257
Bernays P (1922) Die Bedeutung Hilberts für die Philosophie der Mathematik. Die Naturwissenschaften 10:93–99
Brouwer LEJ (1949) Consciousness, philosophy and mathematics. In: Beth EW, Pos HJ, Hollak JHA (eds) Actes du Xme congrès international de philosophie (1948). North-Holland, Amsterdam, pp 1235–1249
Burris S, Sankappavanar HP (2012) A course in universal algebra. The Third Millenium Edition
Cole J (2013) Towards an institutional account of the objectivity, necessity and atemporality of mathematics. Philosophia Mathematica 3(21):9–36
Denney E, Power J, Tourlas K (2006) Hiproofs: a hierarchical notion of proof tree. Electron Notes Theoret Comput Sci 155:341–359
Detlefsen M (2014) Duality, epistemic efficiency & consistency. In: Formalism and beyond. On the nature of mathematical discourse. Godehard (ed) Link, vol 23. Studien zur Logik, Sprachphilosophie und Metaphysik. De Gruyter, Berlin. Chap. 1, pp. 1–24
Detlefsen M, Arana A (2011) Purity of methods. Philosopher 11(2):1–22
Dosen K (2003) Identity of proofs based on normalization and generality. Bull Symbolic Logic 4(9):477–503
Ernest P (1998) Social constructivism as a philosophy of mathematics. State University of New York Press, New York
Feferman S (2009) Conceptions of the continuum. Intellectica 51
Gowers TW (2007) https://gowers.wordpress.com/2007/10/04/whenare-two-proofs-essentially-the-same/
Greeno JG (1983) Conceptual entities. In: Gentner D, Stevens AL (eds) Mental models. Lawrence Erlbaum Associates, Mahwah, pp 227–252
Hersh R, Davis P (1981) The mathematical experience. Houghton Mifflin, Boston
Heyting A (1971) Intuitionism. An introduction. North-Holland, Amstrerdam
Kreisel G (1965) Mathematical logic. Wiley, New York
Prawitz D (1971) Ideas and results in proof theory. In: Fenstad JE (ed) Proceedings of the second Scandinavian Logic Symposium. North-Holland, pp 235–307
Proclus (1873) In: Friedlein G (ed) Primum Euclidis elementorum libri commentarii. Teubner, Leipzig
Russo L (1998) The definitions of fundamental geometric entities contained in book I of Euclid’s elements. Arch Hist Exact Sci 52(3):195–219
Schmidt JV, Venturi G (2022) Fine’s postulationism, objectivity, and mathematical creation. Noesis 38:123–138
Schmidt JV, Venturi G (2023) Axioms and postulates as speech acts. In: Erkenntnis
Simon HA, Hayes JR (1977) Psychological differences among problem isomorphs. In: Potts G (ed) Indiana cognitive symposium. Lawrence Erlbaum Associates, Potomac, pp 21–41
Veblen O, Young JW (1910) Projective geometry, vol 1. Ginn, Boston
Veronese G (1891) Fondamenti della geometria. Tipografia del seminario, Padova
Weber H (1891) Leopold Kronecker. Jahresbericht der Deuschen MathematikerVereinigung 3:5–23
Whitehead AN (1906) The axioms of projective geometry. Cambridge Tracts in Mathematics and Mathematical Physics. Cambridge University Press, Cambridge
Wolstencroft K, Stevens R, Haarslev V (2007) Applying OWL reasoning to genomic data. In: Baker CJG, Cheung K-G (ed) Semantic web: revolutionizing knowledge discovery in the life sciences. Springer, New York, Chap. 11, pp 225–248
Funding
Funding was provided by Fundação de Amparo à Pesquisa do Estado de São Paulo (Grant no. 2016/25891-3), Alexander von Humboldt-Stiftung.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Bianchetti, M., Venturi, G. Formal Ontology and Mathematics. A Case Study on the Identity of Proofs. Topoi 42, 307–321 (2023). https://doi.org/10.1007/s11245-022-09864-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11245-022-09864-4