Robust fitting for generalized additive models for location, scale and shape

Abstract

The validity of estimation and smoothing parameter selection for the wide class of generalized additive models for location, scale and shape (GAMLSS) relies on the correct specification of a likelihood function. Deviations from such assumption are known to mislead any likelihood-based inference and can hinder penalization schemes meant to ensure some degree of smoothness for nonlinear effects. We propose a general approach to achieve robustness in fitting GAMLSSs by limiting the contribution of observations with low log-likelihood values. Robust selection of the smoothing parameters can be carried out either by minimizing information criteria that naturally arise from the robustified likelihood or via an extended Fellner–Schall method. The latter allows for automatic smoothing parameter selection and is particularly advantageous in applications with multiple smoothing parameters. We also address the challenge of tuning robust estimators for models with nonlinear effects by proposing a novel median downweighting proportion criterion. This enables a fair comparison with existing robust estimators for the special case of generalized additive models, where our estimator competes favorably. The overall good performance of our proposal is illustrated by further simulations in the GAMLSS setting and by an application to functional magnetic resonance brain imaging using bivariate smoothing splines.

1 Introduction

Generalized additive models for location, scale and shape (GAMLSS) are flexible nonparametric regression models that have been introduced by Rigby and Stasinopoulos (2005); see also the recent book and tutorial by Stasinopoulos et al. (2017) and Stasinopoulos et al. (2018) for a review. These models allow the use of explanatory variables not only to model the location parameter (e.g., the mean) of a response distribution, like in generalized additive models (GAM; Hastie and Tibshirani 1990), but also the scale and shape parameters. GAMLSSs also go beyond the exponential family of distributions. In fact, the approach can be seen more broadly as a way to model any parameter of any given distribution. As such, some authors refer to it as distributional or multi-parameter regression (e.g., Burke and MacKenzie 2017; Lang et al. 2014; Pan and Mackenzie 2003; Stasinopoulos et al. 2018). Software availability for a wide range of families of distributions, such as the R package gamlss (Stasinopoulos and Rigby 2020), has helped making these models very popular and widely applied in several fields: We can cite Glasbey and Khondoker (2009) (normalizing cDNA microarray), Rudge and Gilchrist (2005) (health impact of temperatures in dwellings), De Castro et al. (2010) (long-term survival models for clinical studies), Beyerlein et al. (2008) (childhood obesity), and Cole et al. (2009) (charts for child growth curves).

The motivation of this paper comes from challenging applications similar to the real data presented in Sect. 5 as an illustration. The study first reported in Landau et al. (2003) investigates differences in the brain physiological response to controlled stimuli between anatomically distinct regions. The continuous response variable consists in the brain activity response measured at voxels in a brain slice (a 2D raster image). The sole explanatory variables are the coordinates identifying the location of each voxel. The measurements are highly noisy, but the nonnegative mean response level and its spread are believed to vary smoothly over the brain slice, thus prompting nonlinear effects for both location and scale parameters of some continuous distribution supported over the positive reals. Wood (2017, p. 329) identified two voxel responses in these data that were deemed too extreme and were then discarded for the subsequent analysis. We believe a robust fitting of a GAMLSS is hence appropriate here, where throughout the paper we understand the term “robust” as implying a bounded maximum bias under arbitrary contamination in the response distribution (e.g., Hampel et al. 1986; Huber and Ronchetti 2009). Such robustness is important here for two reasons: to guarantee that estimates and uncertainties are reliable, and to identify potentially outlying observations in an automated way thanks to robustness weights.

The fitting of GAMLSSs is typically performed by penalized maximum likelihood (ML) estimation. For datasets like the one above, where extreme observations likely occur, the ML estimation procedure suffers from a lack of robustness, meaning that the estimated smooth functions can be distorted by the outliers. Both the nonparametric function estimates themselves and the choice of the smoothing parameters associated to them are affected. To address these issues, we introduce a general robust estimator for GAMLSSs. Our approach covers special cases where robustness has been previously addressed, in particular, in the (extended) GAM context (Alimadad and Salibian-Barrera 2011; Wong et al. 2014; Croux et al. 2012). These works, however, cannot be extended to the more general setting of GAMLSS. Specifically, in contrast with the cited literature which acts at the level of the score equations, we introduce robustness by modifying the objective function following an idea introduced by Eguchi and Kano (2001). We also propose a novel and general procedure to tune the robustness parameter associated with the robust approach. This problematic issue has been partially ignored in the literature for robust (extended) GAMs. For the selection of the smoothing parameters, we additionally propose robust versions of the Akaike information criterion (AIC) and Bayesian information criterion (BIC), that can be typically minimized in a grid search, and an adaptation of the Fellner–Schall automatic multiple smoothing parameter selection method (Wood and Fasiolo 2017), which has important practical advantages. The proposed robust models can be easily used via the newly revised gamlss function in the R package GJRM (Marra and Radice 2020).

Reviewers pointed out the recent publication of a textbook by Rigby et al. (2019) where an alternative robust estimation method for GAMLSSs is presented. This method achieves robustness by winsorizing the observed response through (normalized) quantile residuals, in the spirit of the general robust estimator of Field and Smith (1994). This alternative method is not complete at the time of writing: theoretical properties are lacking, such as the sampling distribution necessary for inference; the correction for Fisher consistency cannot be directly extended beyond continuous families of distribution due to the reliance on quantile residuals; and the challenges of tuning a robust estimator with non-parametric effects and smoothing parameter selection are not discussed. In addition, to the best of our knowledge this method is not implemented in any publicly available software package, thus preventing any meaningful comparison with the method we propose here. Some preliminary simulations in a simple parametric setting with independent and identically distributed data are encouraging for this alternative method, but a thorough comparison in the much broader GAMLSS setting represents future work.

In Sect. 2, we introduce the GAMLSS framework and the related estimation procedure which is based on penalized maximum likelihood. Our proposal is fully introduced in Sect. 3, with subsections devoted to the definition of a penalized robust objective function, theoretical properties and inference, the practical implementation of the estimation procedure, smoothing parameter selection, and the choice of the robustness tuning constant. In Sect. 4, we present two simulation studies to highlight the good behavior of our proposal: one in the GAMLSS setting with a design mimicking the brain imaging data example, and one in the special case of a GAM to allow comparison with existing robust procedure in this context. The brain imaging data illustration is then presented in Sect. 5, while conclusions are given in Sect. 6.

2 GAMLSS framework and penalized estimation

2.1 Framework and notation

Given a sequence of n independent response random variables $Y_1,\ldots ,Y_n$, the generalized additive model for location, scale and shape (GAMLSS; Rigby and Stasinopoulos 2005) for the particular case of a three parameter distribution is defined by

$$\begin{aligned} Y_i&\sim D(\mu _i, \sigma _i, \nu _i), \ i=1,\ldots ,n \nonumber \\ \eta _{1i}&= g_1\left( \mu _i\right) = \beta _{10} + s_{11}(\varvec{x}_{11i}) + \cdots + s_{1 k}(\varvec{x}_{1 k i})\nonumber \\&\quad + \cdots + s_{1 K_1}(\varvec{x}_{1K_1i}), \nonumber \nonumber \\ \eta _{2i}&= g_2\left( \sigma _i\right) = \beta _{20} + s_{21}(\varvec{x}_{21i}) + \cdots + s_{2 k}(\varvec{x}_{2 k i})\\&\quad + \cdots + s_{2 K_2}(\varvec{x}_{2K_2i}),\nonumber \\ \eta _{3i}&= g_3\left( \nu _i\right) = \beta _{30} + s_{31}(\varvec{x}_{31i}) + \cdots + s_{3 k}(\varvec{x}_{3 k i})\nonumber \\&\quad + \cdots + s_{3 K_3}(\varvec{x}_{3K_3i}),\nonumber \end{aligned}$$

(1)

where D denotes a family of distributions canonically parametrized in terms of location $\mu _i$, scale $\sigma _i$ and shape $\nu _i$ which are related to the respective predictors $\eta _{di}$ via specified link functions $g_d$, for $d=1,2,3$, $\beta _{d0}\in \mathbb {R}$ are overall intercepts, $\varvec{x}_{d k i}$ denotes the kth subvector of covariates pertaining to term d and observation i (which includes binary, categorical, discrete, and continuous variables), and the $K_d$ functions $s_{d k}(\cdot )$ represent generic effects of covariates (linear or not). The distributional assumption of $Y_i$ is understood to be conditional on all covariates. We approximate each $s_{d k}(\varvec{x}_{d k i})$ by a linear combination of $J_{d k}$ basis functions $b_{d k j}(\varvec{x}_{d k i})$ and regression coefficients $\beta _{d k j}\in \mathbb {R}$ (e.g., Wood 2017)

$$\begin{aligned} s_{d k}(\varvec{x}_{d k i}) \approx \sum _{j=1}^{J_{d k}} \beta _{d k j} b_{d k j}(\varvec{x}_{d k i}). \end{aligned}$$

This allows the model summarized by (1) to be written in a compact form for the random vector $\varvec{Y}= (Y_1,\ldots ,Y_n)^\top$ as $\varvec{Y}\sim D(\varvec{\mu }, \varvec{\sigma }, \varvec{\nu })$ by some slight abuse of notation, where the parameter vectors $\varvec{\mu }=(\mu _1,\ldots ,\mu _n)^\top$, $\varvec{\sigma }=(\sigma _1,\ldots ,\sigma _n)^\top$ and $\varvec{\nu }=(\nu _1,\ldots ,\nu _n)^\top$ are modeled through

$$\begin{aligned} \begin{aligned} \varvec{\eta }_{1}&= g_1(\varvec{\mu }) = \mathbf {1}_n\beta _{10} + \mathbf {X}_{11}\varvec{\beta }_{11}+\cdots +\mathbf {X}_{1K_1}\varvec{\beta }_{1K_1} = \mathbf {X}_1\varvec{\beta }_1,\\ \varvec{\eta }_{2}&= g_2(\varvec{\sigma }) = \mathbf {1}_n\beta _{20} + \mathbf {X}_{21}\varvec{\beta }_{21}+\cdots +\mathbf {X}_{2K_2}\varvec{\beta }_{2K_2} = \mathbf {X}_2\varvec{\beta }_2,\\ \varvec{\eta }_{3}&= g_3(\varvec{\nu }) = \mathbf {1}_n\beta _{30} + \mathbf {X}_{31}\varvec{\beta }_{31}+\cdots +\mathbf {X}_{3K_3}\varvec{\beta }_{3K_3} = \mathbf {X}_3\varvec{\beta }_3, \end{aligned} \end{aligned}$$

(2)

where the functions $g_d$ are applied element-wise, $\mathbf {1}_n$ is an n-dimensional vector of ones, the $(n \times J_{d k})$ matrix $\mathbf {X}_{d k}$ has (i, j)th element $b_{d k j}(\varvec{x}_{d k i})$, and $\varvec{\beta }_{d k} = (\beta _{d k 1}, \ldots , \beta _{d k J_{k d}})^\top$. The predictors can thus be rewritten as $\varvec{\eta }_d=\mathbf {X}_d \varvec{\beta }_d$, where $\mathbf {X}_d = (\mathbf {1}_n, \mathbf {X}_{d 1}, \ldots , \mathbf {X}_{d K_d})$ and $\varvec{\beta }_d = (\beta _{d 0}, \varvec{\beta }_{d 1}^\top , \ldots , \varvec{\beta }_{d K_d}^\top )^\top$. We note that our results and methods here are understood in a fixed-knot framework, i.e., that the number of basis functions is fixed at a high value so that any approximation bias in $s_{d k}(\varvec{x}_{d k i})$ is negligible compared to estimation variability (as in, e.g., Vatter and Chavez-Demoulin 2015).

To enforce a certain degree of smoothness for every approximated $s_{d k}(\cdot )$ function, each $\varvec{\beta }_{d k}$ has an associated quadratic penalty $\lambda _{d k} \varvec{\beta }_{d k}^\top \mathbf {D}_{d k} \varvec{\beta }_{d k}$, where $\mathbf {D}_{d k}$ only depends on the choice of basis functions. The smoothing parameter $\lambda _{d k} \in [0,\infty )$ controls the trade-off between fit and smoothness and plays a crucial role in determining the shape of the estimated $\hat{s}_{d k}(\cdot )$. For $d=1,2,3$, the overall penalty can be written as $\varvec{\beta }_d^\top \mathbf {D}_d \varvec{\beta }_d$, where $\mathbf {D}_d = \mathop {\mathrm {diag}}(0,\lambda _{d 1}\mathbf {D}_{d 1}, \ldots , \lambda _{d K_d}\mathbf {D}_{d K_d})$. Following Wood (2017), the approximated $s_{d k}(\cdot )$ smooth functions are subject to centering constraints to ensure identifiability. Examples of smooth function specification include one-dimensional, multi-dimensional, random field and random effect smoothers; see e.g., Wood (2017) for details. Note that we have considered distributions with up to three parameters (location, scale and shape), hence the adopted notation with $d=1,2,3$, yet the proposed framework can be conceptually extended to distributions with more parameters in a straightforward manner. The families of distributions implemented in this work are listed in Table S1 in “Web Appendix D”.

2.2 Penalized log-likelihood

Let $\varvec{\delta }= (\varvec{\beta }_{1}^\top ,\varvec{\beta }_{2}^\top ,\varvec{\beta }_{3}^\top )^\top \in \varvec{\Delta }\subseteq \mathbb {R}^{p}$ denote the full model parameter vector. Given a sample of n realizations $y_1,\ldots ,y_n$, the log-likelihood function corresponding to (2) is given by

$$\begin{aligned} \ell (\varvec{\delta }) = \sum _{i=1}^n \ell (\varvec{\delta })_i = \sum _{i=1}^n \log f\left( y_{i}|\mu _{i}, \sigma _{i}, \nu _{i}\right) , \end{aligned}$$

(3)

where $f\left( y_{i}|\cdot \right)$ can either denote the probability density function (pdf) or the probability mass function (pmf) corresponding to the distribution D. Because of the flexibility of the smooth terms, the use of an unpenalized optimization algorithm is likely to result in unduly wiggly estimates (e.g., Wood 2017). Estimation is thus typically performed by maximizing the penalized version $\ell _p(\varvec{\delta }) = \ell (\varvec{\delta }) - \frac{1}{2} \varvec{\delta }^\top \mathbf {S}\varvec{\delta }$, where $\mathbf {S}= \mathop {\mathrm {diag}}(\mathbf {D}_{1},\mathbf {D}_{2},\mathbf {D}_{3})$. The smoothing parameters contained in the $\mathbf {D}_d$’s make up the vector $\varvec{\lambda }= (\varvec{\lambda }_{1}^\top ,\varvec{\lambda }_{2}^\top ,\varvec{\lambda }_{3}^\top )^\top$. Estimation of $\varvec{\delta }$ is typically achieved for a given value of $\varvec{\lambda }$, while the selection of $\varvec{\lambda }$ is often performed by minimizing some prediction error criterion, either as an outer optimization or by alternating the estimation of $\varvec{\delta }$ given $\varvec{\lambda }$ and the selection of $\varvec{\lambda }$ given $\varvec{\delta }$ (Wood 2017). Examples of such a criterion include cross-validation (CV; e.g., Hastie and Tibshirani 1990) and generalized cross-validation (GCV; Craven and Wahba 1979) estimates of prediction error, as well as estimates of the Kullback–Leibler divergence between a true model and the fitted one such as the AIC, and the Generalized Information Criterion (GIC) of Konishi and Kitagawa (1996).

3 Robust estimation

The estimation procedures mentioned in the previous section rely on strict distributional assumptions. These methods are known to be highly sensitive to deviations from model assumptions (e.g., Hampel et al. 1986; Huber and Ronchetti 2009). To this end, we propose a general robust fitting approach, which is valid for the entire class of GAMLSS and that directly yields robust criteria for the selection of smoothing parameters.

3.1 Penalized robustified log-likelihood

Based on the $\Psi$-divergence approach of Eguchi and Kano (2001), we introduce the robustified log-likelihood

$$\begin{aligned} \tilde{\ell }(\varvec{\delta }) = \sum _{i=1}^n \rho _c\big (\ell (\varvec{\delta })_i\big ) - b_{\rho }(\varvec{\delta }), \end{aligned}$$

where, for a given $\varvec{\delta }$, the user-specified $\rho _c$ function is designed to reduce low log-likelihood values $\ell (\varvec{\delta })_i$ while leaving large log-likelihood values essentially unchanged, and

$$\begin{aligned} b_{\rho }(\varvec{\delta }) = \sum _{i=1}^n b_{\rho }(\varvec{\delta })_i = \sum _{i=1}^n \int \rho _c^\star \big (\log f(y|\mu _{i},\sigma _{i},\nu _{i})\big ) \, \mathrm {d}y \end{aligned}$$

(4)

is a correction term ensuring Fisher consistency (see Theorem 1 in Sect. 3.2), where $\rho _c^\star$ is directly derived from the specified $\rho _c$ through

$$\begin{aligned} \rho _c^\star (z) = \int _{-\infty }^z \exp (s) \rho _c'(s) \, \mathrm {d}s, \end{aligned}$$

where $\rho _c'(s) = \partial \rho _c(s) / \partial s$, see Eguchi and Kano (2001, Section 2). The $\rho$ function is indexed by a so-called robustness tuning constant $c>0$ which regulates the trade-off between, on the one hand, the loss of estimation efficiency in the ideal case that the data exactly come from the assumed GAMLSS, and, on the other hand, the maximum bias induced by some contamination whenever the data do not come from the assumed GAMLSS. For any given c, $\rho _c$ is assumed to be convex, monotonically increasing and twice continuously differentiable over $\mathbb {R}$ and have bounded first derivative $\rho _c'$ within [0, 1]. The latter can be interpreted as a multiplicative robustness weight, as one would do when weighting the estimating equations in robust M-estimation. The important difference here is that the “robustification” happens at the log-likelihood level and not by directly applying weights at the score level, such as in Wong et al. (2014) for example. An advantage of our approach is that it leads to a natural definition of robust criteria for the selection of smoothing parameters (see Sect. 3.2).

Eguchi and Kano (2001) proposed the following log-logistic $\rho$ function:

$$\begin{aligned} \rho _c(z) = \log \frac{1+\exp (z+c)}{1+\exp (c)}, \quad c>0, \end{aligned}$$

with corresponding $\rho _c^\star (z) = \exp (z) - \exp (c)\log \big (1+\exp (z+c)\big )$ and first derivative $\rho _c'(z) = \exp (z+c)/\big (1+\exp (z+c)\big )$. Web Figure S1 in “Web Appendix C” displays the log-logistic $\rho _c$ and its first derivative. It illustrates how a smaller value of c leads to an earlier flattening of the $\rho$ function applied on log-likelihood contributions, thus limiting earlier their impact. Note that $\lim _{c\rightarrow \infty }\rho _c(z) = z$ so that an increasingly large c value leads to the (non-robust) original $\ell (\varvec{\delta })$. We discuss the choice of c in Sect. 3.5. We note that the particular form of $\rho _c$ matters little beyond the requirements mentioned earlier and summarized in condition (C1) in “Web Appendix A”; it is not part of the model or the fit since no assumptions are being made about the subset of the data that may not conform to the model assumptions.

For a given smoothing parameter $\varvec{\lambda }$, we define our robust estimator $\hat{\varvec{\delta }} = \hat{\varvec{\delta }}(\varvec{\lambda })$ by maximizing the penalized robustified log-likelihood

$$\begin{aligned} \hat{\varvec{\delta }} = \mathop {\hbox {arg max}}\limits _{\varvec{\delta }} \tilde{\ell }_{p}(\varvec{\delta }) = \mathop {\hbox {arg max}}\limits _{\varvec{\delta }}\left\{ \tilde{\ell }(\varvec{\delta }) - \frac{1}{2} \varvec{\delta }^\top \mathbf {S}\varvec{\delta }\right\} , \end{aligned}$$

(5)

where the penalty is identical to that of non-robust penalized estimation. Our robustification scheme targets only deviations in the response variable, the latter which does not appear in $\varvec{\delta }^\top \mathbf {S}\varvec{\delta }$ so that only contributions to the unpenalized log-likelihood $\ell (\varvec{\delta })$ need to be accounted for. The robust estimator is thus the solution in $\varvec{\delta }$ to the following estimating equations (first-order conditions):

$$\begin{aligned} \mathbf {0}&= \frac{\partial \tilde{\ell }(\varvec{\delta })}{\partial \varvec{\delta }} - \mathbf {S}\varvec{\delta }= \sum _{i=1}^n \rho _c'\big (\ell (\varvec{\delta })_i\big )\frac{\partial \ell (\varvec{\delta })_i}{\partial \varvec{\delta }} - \frac{\partial b_{\rho }(\varvec{\delta })}{\partial \varvec{\delta }} - \mathbf {S}\varvec{\delta }. \end{aligned}$$

(6)

In (6), the response variable $Y_i$ only appears through $\ell (\varvec{\delta })_i$ since $b_{\rho }$ is an expectation. Thus $\rho _c'$ indeed plays the role of a multiplicative weight within [0, 1] which limits the impact of potentially deviating observations given some $\varvec{\delta }$. This robustness weight is proved useful both for selecting c (see Sect. 3.5) and as a diagnostic tool (see the data analysis in Sect. 5).

3.2 Asymptotic properties and inference

The unpenalized robust estimator which maximizes $\tilde{\ell }(\varvec{\delta })$ admits a statistical M-functional representation $\varvec{T}(F)$, for some generic probability distribution F, which is the solution in $\varvec{\delta }$ to $\mathbb {E}\left[ \psi (Y,\varvec{\delta })\right] = \mathbf {0}$ where

$$\begin{aligned} \psi (Y,\varvec{\delta })= & {} \rho _c'\big (\log f(Y|\mu ,\sigma ,\nu )\big )\frac{\partial \log f(Y|\mu ,\sigma ,\nu )}{\partial \varvec{\delta }} \nonumber \\&- \frac{\partial }{\partial \varvec{\delta }}\mathbb {E}\left[ \rho _c^\star \big (\log f(Y|\mu ,\sigma ,\nu )\big ) \right] \end{aligned}$$

(7)

with expectations taken under F. Thus, the finite-sample solution in $\varvec{\delta }$ to

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n \left\{ \rho _c'\big (\ell (\varvec{\delta })_i\big )\frac{\partial \ell (\varvec{\delta })_i}{\partial \varvec{\delta }} - \frac{\partial b_{\rho }(\varvec{\delta })_i}{\partial \varvec{\delta }}\right\} = \mathbf {0} \end{aligned}$$

can be written as $\varvec{T}(F_n)$, where $F_n$ denotes the empirical distribution putting mass 1/n on each observation. $\varvec{T}(F_n)$ amounts to an unpenalized robust estimator.

To discuss the asymptotic properties of the proposed (penalized) robust estimator, we define $\varvec{\delta }_0$ as the parameter value to which the unpenalized MLE maximizing $\ell (\varvec{\delta })$ in (3) converges, as $n\rightarrow \infty$. By viewing $\varvec{\delta }_0$ as the “true” parameter that generates the data under distribution D with parameters defined in Eq. (2), Theorem 1 establishes the Fisher consistency of $\hat{\varvec{\delta }}$ and its asymptotic distribution; the proof is deferred to “Web Appendix A”.

Theorem 1

Under conditions (C1)–(C5) in “Web Appendix A”, as $n\rightarrow \infty$ the penalized robust estimator $\hat{\varvec{\delta }}$ admits the same M-functional representation $\varvec{T}$ as the unpenalized robust estimator and we have $\varvec{T}(D) = \varvec{\delta }_0$. Moreover, $\sqrt{n}(\hat{\varvec{\delta }}-\varvec{\delta }_0) \underset{n\rightarrow \infty }{\overset{d}{\longrightarrow }} \text {N}(\mathbf {0}, \mathbf {V}(\varvec{\delta }_0))$, where the asymptotic covariance matrix is given by the so-called sandwich formula $\mathbf {V}(\varvec{\delta }) = \mathbf {M}(\varvec{\delta })^{-1} \mathbf {Q}(\varvec{\delta }) \mathbf {M}(\varvec{\delta })^{-\mathsf T}$, where

$$\begin{aligned}&\mathbf {M}(\varvec{\delta }) = -\mathbb {E}\left[ \frac{\partial ^2 \tilde{\ell }(\varvec{\delta })}{\partial \varvec{\delta }\partial \varvec{\delta }^\top } \right] \quad \text {and} \quad \nonumber \\&\mathbf {Q}(\varvec{\delta }) = \mathbb {E}\left[ \left( \frac{\partial \tilde{\ell }(\varvec{\delta })}{\partial \varvec{\delta }} \right) \left( \frac{\partial \tilde{\ell }(\varvec{\delta })}{\partial \varvec{\delta }} \right) ^\top \right] , \end{aligned}$$

(8)

with expectations taken under the assumed distribution D.

In Theorem 1, $\varvec{T}(D) = \varvec{\delta }_0$ means that $\hat{\varvec{\delta }}$ is Fisher consistent: It returns the true parameter when $\varvec{T}$ is evaluated at the assumed distribution D, which implies that $\hat{\varvec{\delta }}$ is asymptotically unbiased for $\varvec{\delta }_0$. The influence function (IF; Hampel 1974) of the Fisher consistent functional $\varvec{T}$ is proportional to the score $\psi (Y,\varvec{\delta })$ given in (7). This score being bounded in the response variable Y thanks to $\rho _c' \in [0,1]$, the IF is itself bounded. This guarantees a bounded maximum asymptotic bias under arbitrary contamination in Y, which is the main robustness property of $\hat{\varvec{\delta }}$.

Remark 1

The asymptotic variance $\mathbf {V}(\varvec{\delta }_0)$ in Theorem 1 corresponds to an unpenalized robust estimation because we assume the usual asymptotically vanishing penalty for consistency (see condition (C5) in “Web Appendix A”). A better approximation of the finite-sample covariance matrix with nonzero penalty can be obtained from a Taylor expansion of the penalized robustified score, as given in Eq. (2) in “Web Appendix A”. It amounts to $\mathbf {V}_p(\varvec{\delta }_0) = \mathbf {M}_p(\varvec{\delta }_0)^{-1} \mathbf {Q}(\varvec{\delta }_0) \mathbf {M}_p(\varvec{\delta }_0)^{-\mathsf T}$, where $\mathbf {M}_p(\varvec{\delta }) = -\mathbb {E}\left[ \frac{\partial ^2 \tilde{\ell }_{p}(\varvec{\delta })}{\partial \varvec{\delta }\partial \varvec{\delta }^\top } \right] = \mathbf {M}(\varvec{\delta }) + \mathbf {S}$. In these expressions, $\varvec{\delta }_0$ being unknown in practice one would typically “plug-in” the estimate $\hat{\varvec{\delta }}$ to compute standard errors. This allows for the computation of approximate (point-wise) confidence intervals, which can then be interpolated for confidence bands for nonlinear effects. See, for instance, Croux et al. (2012, p. 39) for the analogue in the extended GAM setting.

Remark 2

An alternative covariance can be computed following an empirical Bayes approach, which is often reported to lead to good finite-sample coverage of confidence intervals in the frequentist sense (see, e.g., Marra and Wood 2012; Wood 2017). For a given $\varvec{\lambda }$, viewing the quadratic penalty as an improper Gaussian prior distribution for $\varvec{\delta }$ (seen as a random vector here), with mean zero and covariance $\mathbf {S}^{-1}$, the joint density of $(\varvec{Y},\varvec{\delta })$ is given, up to normalization constants, by $L(\varvec{y},\varvec{\delta };\varvec{\lambda }) = \exp \big (\tilde{\ell }(\varvec{\delta })\big ) \exp \big (-\varvec{\delta }^\top \mathbf {S}\varvec{\delta }/2\big )|\mathbf {S}|^{1/2}$, with $|\cdot |$ denoting matrix determinant. We seek the covariance of the posterior distribution of $\varvec{\delta }| \varvec{Y}$, as the posterior mode corresponds to the robust estimate $\hat{\varvec{\delta }}$. As in Wood and Fasiolo (2017), a second-order Taylor expansion of the posterior log-density about its mode reveals that as $n\rightarrow \infty$ the posterior distribution approaches a multivariate Gaussian with covariance given by $\mathbf {M}_p(\hat{\varvec{\delta }})^{-1}$. Our experience is that the observed version of this posterior covariance matrix, $\widehat{\mathbf {M}}_p(\hat{\varvec{\delta }})^{-1} = \left( \widehat{\mathbf {M}}(\hat{\varvec{\delta }}) + \mathbf {S}\right) ^{-1}$, where $\widehat{\mathbf {M}}(\varvec{\delta }) = -\frac{\partial ^2 \tilde{\ell }(\varvec{\delta })}{\partial \varvec{\delta }\partial \varvec{\delta }^\top }$, can be used as a computationally efficient alternative to $\mathbf {V}_p(\hat{\varvec{\delta }})$.

The effective degrees of freedom (edf) of smooth terms are a valuable tool for assessing the degree of smoothness achieved by a fit. We follow the discussion of Wood (2017, Chapter 6) based on links with generalized linear mixed models and restricted ML estimation to obtain that the edf of a GAMLSS robust fit is $\text {tr}\big \{\widehat{\mathbf {M}}_p(\hat{\varvec{\delta }})^{-1}\widehat{\mathbf {Q}}(\hat{\varvec{\delta }})\big \} = \text {tr}\big \{(\widehat{\mathbf {M}}(\hat{\varvec{\delta }}) + \mathbf {S})^{-1}\widehat{\mathbf {Q}}(\hat{\varvec{\delta }})\big \}$, where $\widehat{\mathbf {Q}}(\varvec{\delta }) = \left( \frac{\partial \tilde{\ell }(\varvec{\delta })}{\partial \varvec{\delta }}\right) \left( \frac{\partial \tilde{\ell }(\varvec{\delta })}{\partial \varvec{\delta }}\right) ^\top$. This term matches the “penalty term” of our robust AIC introduced in Sect. 3.4 below.

3.3 Estimation approach and implementation

To maximize (5), we have modified the efficient and stable trust region algorithm of Marra et al. (2017) to accommodate the robustified objective function and corresponding correction term $b_{\rho }(\varvec{\delta })$. Estimation of $\varvec{\delta }$ and $\varvec{\lambda }$ is carried out as follows. At iteration a, holding $\varvec{\lambda }$ fixed and for some tuning constant value c, for a given $\varvec{\delta }^{[a]}$ we maximize Eq. (5) using a trust region algorithm (Conn et al. 2000):

$$\begin{aligned} \varvec{\delta }^{[a+1]} = \varvec{\delta }^{[a]} + \mathop {\hbox {arg min}}\limits _{\varvec{e}:\Vert \varvec{e}\Vert \le \Delta ^{[a]}} \breve{\tilde{\ell }}_p(\varvec{e};\varvec{\delta }^{[a]}), \end{aligned}$$

(9)

where $\Vert \cdot \Vert$ denotes the Euclidean norm, $\Delta ^{[a]}$ is the radius of the trust region which is adjusted throughout the iterations, $\breve{\tilde{\ell }}_p(\varvec{e};\varvec{\delta }^{[a]}) = -\left( \tilde{\ell }_p(\varvec{\delta }^{[a]}) + \varvec{e}^\top \varvec{g}_p(\varvec{\delta }^{[a]}) + \frac{1}{2}\varvec{e}^\top \mathbf {H}_p(\varvec{\delta }^{[a]})\varvec{e}\right)$, $\varvec{g}_p(\varvec{\delta }^{[a]}) = \varvec{g}(\varvec{\delta }^{[a]}) - \mathbf {S}\varvec{\delta }^{[a]}$ and $\mathbf {H}_p(\varvec{\delta }^{[a]}) = \mathbf {H}(\varvec{\delta }^{[a]}) - \mathbf {S}$, and where the vector $\varvec{g}(\varvec{\delta }^{[a]})$ consists of the stacked $\varvec{g}_d(\varvec{\delta }^{[a]}) = \partial \tilde{\ell }(\varvec{\delta }) / \partial \varvec{\beta }_d |_{\varvec{\beta }_d = \varvec{\beta }_d^{[a]}}$ for $d=1,2,3$, and the Hessian matrix $\mathbf {H}$ has elements $\mathbf {H}(\varvec{\delta }^{[a]})_{d,h} = \partial ^2 \tilde{\ell }(\varvec{\delta })/\partial \varvec{\beta }_d \partial \varvec{\beta }_h^\top |_{\varvec{\beta }_d={\varvec{\beta }}_d^{[a]},\varvec{\beta }_h={\varvec{\beta }}_h^{[a]}}$, for $d,h=1,2,3$. Equation (9) uses a quadratic approximation of $-\tilde{\ell }_p$ about $\varvec{\delta }^{[a]}$ (the so-called model function) in order to choose the best $\varvec{e}^{[a+1]}$ within the ball centered in $\varvec{\delta }^{[a]}$ of radius $\Delta ^{[a]}$, the trust region. Close to the converged solution, the trust region usually behaves like an unconstrained optimization algorithm.

Trust region algorithms have several advantages over classical alternatives. For instance, in line search methods, when an iteration falls in a long plateau region, the search for step $\varvec{\delta }^{[a+1]}$ can occur so far away from $\varvec{\delta }^{[a]}$ that the evaluation of the model log-likelihood may be indefinite or not finite, in which case the user’s intervention is required. Trust region methods, on the other hand, always solve the sub-problem (9) before evaluating the objective function. So, if $\tilde{\ell }_p$ is not finite at the proposed $\varvec{\delta }^{[a+1]}$ then step $\varvec{e}^{[a+1]}$ is rejected, the trust region shrunken, and the optimization computed again. The radius is also reduced if there is no agreement between the model and objective functions (i.e., the proposed point in the region is not better than the current one). Reversibly, if an agreement occurs, the trust region is expanded for the next iteration. In summary, $\varvec{\delta }^{[a+1]}$ is accepted if it improves over $\varvec{\delta }^{[a]}$ and allows for the evaluation of $\breve{\tilde{\ell }}_p$, whereas the reduction/expansion of $\Delta ^{[a+1]}$ is based on the similarity between model and objective functions. Theoretical and practical details of the method can be found in Nocedal and Wright (2006, Chapter 4) and Geyer (2015). The latter also discusses the necessary modifications to the sub-problem (9) and the radius for ill-scaled variables.

The analytical score and Hessian of (the non-robust) $\ell (\varvec{\delta })$ can be derived in a modular way. This allows for a direct extension to other families of distributions not included in Table 1 in “Web Appendix D” as long as their pdf/pmf are known and their derivatives with respect to their parameters exist. Regarding the optimization of the robustified $\tilde{\ell }_p(\varvec{\delta })$, the integral defining $b_{\rho }(\varvec{\delta })$ in (4), as well as its derivatives, in general have to be approximated. For discrete distributions over countably infinite supports, this amounts to a straightforward truncation of a converging infinite sum. For continuous distributions, we rely on a unidimensional adaptive Gaussian quadrature rule for which we compute data-based finite bounds for numerical stability and to increased speed.

The procedures are all implemented in the gamlss function in the R package GJRM (Marra and Radice 2020). In “Web Appendix E”, we provide some R code and brief explanations on the usage of this function.

3.4 Robust selection of smoothing parameters

Our robustification scheme with $\rho _c$ directly applied on log-likelihood contributions has the advantage of yielding a natural robust AIC (RAIC). Following the construction of the generalized information criterion (GIC) of Konishi and Kitagawa (1996), we can define the Kullback–Leibler divergence $d_{\text {KL}}$ between the true distribution G that generated the data, with density g, and the distribution corresponding to our robustified likelihood (up to normalization constants) as

$$\begin{aligned} d_{\text {KL}}= & {} \mathbb {E}_G \big [ \log \big (g(Y)/\exp (\tilde{\ell }(\varvec{\delta },Y))\big ) \big ] \nonumber \\= & {} \mathbb {E}_G[\log g(Y)] - \mathbb {E}_G[\tilde{\ell }(\varvec{\delta },Y)], \end{aligned}$$

(10)

where $\tilde{\ell }(\varvec{\delta },Y) = \rho _c\big (\log f(Y|\mu ,\sigma ,\nu )\big ) - \int \rho _c^\star \big (\log f(y|\mu ,\sigma ,\nu )\big ) \, \mathrm {d}y$. The generic random variable Y here stands for an out-of-sample observation to be predicted, thus $d_{\text {KL}}$ represents a measure of prediction error. Minimizing $d_{\text {KL}}$ with respect to $\varvec{\delta }$ is equivalent to maximizing $\mathbb {E}_G[\tilde{\ell }(\varvec{\delta },Y)]$ since the first term on the right hand side of (10) is a constant. But because G is unknown, the estimator $(1/n)\sum _{i=1}^n \tilde{\ell }(\varvec{\delta },Y_i)$ is used, which is biased for $\mathbb {E}_G[\tilde{\ell }(\varvec{\delta },Y)]$. In the GIC framework, the first-order correction of this bias depends on the estimator used for $\varvec{\delta }$. We consider here the penalized robust estimator $\hat{\varvec{\delta }}$, so that by Theorem 2.2 of Konishi and Kitagawa (1996) the bias correction amounts to $\text {tr}\big \{\mathbf {M}_p(\varvec{\delta })^{-1}\mathbf {Q}(\varvec{\delta })\big \} = \text {tr}\big \{(\mathbf {M}(\varvec{\delta }) + \mathbf {S})^{-1}\mathbf {Q}(\varvec{\delta })\big \}$. Thus we define the RAIC as

$$\begin{aligned} \text {RAIC}(\varvec{\lambda }) = -2 \tilde{\ell }(\varvec{\delta }) + 2\text {tr}\big [(\widehat{\mathbf {M}}(\varvec{\delta }) + \mathbf {S})^{-1}\widehat{\mathbf {Q}}(\varvec{\delta })\big ], \end{aligned}$$

(11)

where recall that $\mathbf {S}=\mathbf {S}(\varvec{\lambda })$, and the observed matrices $\widehat{\mathbf {M}}(\varvec{\delta })$ and $\widehat{\mathbf {Q}}(\varvec{\delta })$ allow for fast computations. Selecting $\varvec{\lambda }$ can thus be done by minimizing $\text {RAIC}(\varvec{\lambda })$. In (11), since all terms are based on the robustified $\tilde{\ell }(\varvec{\delta })$, the RAIC naturally inherits robustness and the selected $\varvec{\lambda }$ is thus expected to remain stable in the presence of model deviations.

Minimizing an AIC-type criterion for smoothing parameter selection is known to favor more complex models, with function estimates more on the wiggly side. As this feature may carry over to our RAIC, an alternative is to consider a robust version of the Bayesian information criterion where its heavier penalty coefficient ($\log (n)$ rather than 2) generally favors simpler models, with smoother function estimates. Similarly to Wong et al. (2014), in our setting a robust BIC (RBIC) is naturally given by

$$\begin{aligned} \text {RBIC}(\varvec{\lambda }) = -2 \tilde{\ell }(\varvec{\delta }) + \log (n)\text {tr}\big [(\widehat{\mathbf {M}}(\varvec{\delta }) + \mathbf {S})^{-1}\widehat{\mathbf {Q}}(\varvec{\delta })\big ]. \end{aligned}$$

That being said, the proposed RAIC and RBIC procedures involve two nested optimizations: an inner optimization for computing $\hat{\varvec{\delta }}$ given $\varvec{\lambda }$, and an outer optimization over $\varvec{\lambda }$. The high computational cost involved makes the selection of $\varvec{\lambda }$ nearly unfeasible, or unbearably slow, whenever more than one or two smoothers are considered. We therefore propose an alternative robust selection method that can be automated as part of the estimation process with little computational overhead. This alternative is a robust version of the Fellner–Schall method recently introduced in Wood and Fasiolo (2017), which we will call the extended Fellner–Schall (EFS) method. “Web Appendix B” provides the detailed development, the main ideas can be summarized as follows. First, we take the empirical Bayes viewpoint as in Remark 2 in Sect. 3.2 to consider the quadratic penalty as an improper Gaussian prior on $\varvec{\delta }$, resulting in the joint (robustified) likelihood $L(\varvec{y},\varvec{\delta };\varvec{\lambda })$. Next, we approximate the integral defining the marginal likelihood $L(\varvec{y};\varvec{\lambda }) = \int _{\varvec{\Delta }} L(\varvec{y},\varvec{\delta };\varvec{\lambda }) \,\mathrm {d}\varvec{\delta }$ by Laplace’s method. By considering the estimate $\hat{\varvec{\delta }} = \hat{\varvec{\delta }}(\varvec{\lambda })$ as based on a previous iterate for $\varvec{\lambda }$, we obtain a tractable expression for (the Laplace-approximated) $\partial \log L(\varvec{y};\varvec{\lambda }) / \partial \varvec{\lambda }$. Finally, we follow the heuristic reasoning of Wood and Fasiolo (2017) to derive the following update from iteration [k] to $[k+1]$ for all elements of $\varvec{\lambda }$:

$$\begin{aligned} \lambda ^{[k+1]}_j&= \lambda ^{[k]}_j \times \frac{\text{ tr }\big \{\mathbf {S}(\varvec{\lambda }^{[k]})^{-1} \left. \partial \mathbf {S}(\varvec{\lambda })/\partial \lambda _j\right| _{\varvec{\lambda }=\varvec{\lambda }^{[k]}}\big \} - \text{ tr }\big \{\widehat{\mathbf {M}}_p(\hat{\varvec{\delta }})^{-1} \left. \partial \mathbf {S}(\varvec{\lambda })/\partial \lambda _j\right| _{\varvec{\lambda }=\varvec{\lambda }^{[k]}} \big \}}{\hat{\varvec{\delta }}^\top \big (\partial \mathbf {S}(\varvec{\lambda })/\partial \lambda _j|_{\varvec{\lambda }=\varvec{\lambda }^{[k]}}\big ) \hat{\varvec{\delta }}}, \end{aligned}$$

where $\hat{\varvec{\delta }} = \hat{\varvec{\delta }}(\varvec{\lambda }^{[k]})$ here. In this expression, $\partial \mathbf {S}(\varvec{\lambda })/\partial \lambda _j$ is straightforward to write down and implement since $\mathbf {S}(\varvec{\lambda })$ is block-diagonal and each block is typically linear in the components of $\varvec{\lambda }$ and only involves the (known) basis functions. We note that under the conditions of Theorem 1 the update guarantees by construction that $\varvec{\lambda }$ remains positive and that the iterates converge whenever the gradient with respect to $\varvec{\lambda }$ gets arbitrarily close to zero. This update rule can thus be alternated with computing $\hat{\varvec{\delta }}$ in an automated and efficient way since both rely on similar quantities (see Sect. 3.3).

Remark 3

The proposed EFS method is simple to implement and avoids unfeasible grid searches. All that is required is a set of explicit formulas, as given above, to update $\varvec{\lambda }$ in order to increase the (Laplace-approximated) marginal robustified log-likelihood. Our derivation also highlights the method’s broader appeal since it can be easily adapted to modeling situations requiring the use of non-standard models and estimators (i.e., beyond the robust estimation in this paper) as long as a Laplace-approximated marginal likelihood is available.

3.5 Choice of the Robustness tuning constant

The robustness tuning constant c regulates how early $\rho _c$ starts to diminish the contribution of an observation to the objective function $\tilde{\ell }$. The choice of c is typically made before fitting the model to data by targeting a certain loss of estimation efficiency of the robust estimator relative to the MLE at the assumed model. With strictly parametric models, the usual criterion is the ratio of the traces of the asymptotic covariance matrices of the model parameters. But with non-parametric models, where basis function coefficients are subject to some smoothness constraint (as is the case here) the asymptotic covariance matrices of the penalized MLE and of the robust estimator are not necessarily comparable. The reason is that robust estimation may achieve a different degree of smoothness, i.e., a different bias-variance trade-off stemming from different $\varvec{\lambda }$ values selected by minimizing some prediction error criterion. If the two estimators achieve different degrees of smoothness, then the coefficients variances are not necessarily on the same scale and are thus not comparable. One may constrain the smoothness to be similar between the two estimation methods, but this would defeat the purpose of robustness: we are indeed interested in potential differences between the fitted functions and typically suspect that deviating observations may push classical estimates to be too wiggly. Hence, the need for a different criterion for the choice of c. We note that previous works (Alimadad and Salibian-Barrera 2011; Croux et al. 2012; Wong et al. 2014) have not discussed this important issue, resorting to somewhat default values for c taken from strictly parametric cases.

We propose a novel general criterion for the selection of the tuning constant c which covers both additive models and strictly parametric ones. It is simulation-based and relies on the heuristic idea of controlling how the robustness weights at the score level (represented here by $\rho _c'$) behave under data generated from the assumed model. Our procedure is as follows:

• Step 1: For a given tuning constant value c, compute the robust estimator $\hat{\varvec{\delta }}_c$ on the original data by maximizing (5), including the optimal smoothing parameter $\hat{\varvec{\lambda }}_c$.

• Step 2: For a large number of Monte Carlo replications B, for $b \in \{1,\ldots ,B\}$ repeat:

  • (a) Generate a response vector $\varvec{y}_b$ given the original design and covariates according to the assumed model in (2) using $\hat{\varvec{\delta }}_c$ as generating parameter.

  • (b) Use both $\hat{\varvec{\delta }}_c$ and $\hat{\varvec{\lambda }}_c$ to compute the vector of robustness weights $(w_{b,1},\ldots ,w_{b,n})^\top$, where $w_{b,i} = \rho _c'(\ell (\hat{\varvec{\delta }}_c)_{b,i})$ with $\ell (\hat{\varvec{\delta }}_c)_{b,i}$ denoting the log-likelihood value corresponding to the ith entry in $\varvec{y}_b$. Compute the sum of the robustness weights $w_b = \sum _{i=1}^n w_{i,b}$.

• Step 3: The criterion corresponding to c is the median downweighting proportion (MDP) over the B independent replicates: $\text {median}\{w_1/n,\ldots ,w_B/n\}$.

• Step 4: Repeat Steps 1–3 to find the c value matching a target MDP (e.g., $\text {MDP}=0.95$).

Since $\rho _c'(\ell (\varvec{\delta })_{b,i}) \in [0,1]$ for any $\varvec{\delta }$ by construction, the ratio $w_b/n$ indeed represents how much downweighting has occurred on a particular sample $\varvec{y}_b$. The value $w_b/n=1$ indicates no downweighting at all, i.e., the corresponding estimate is the penalized MLE. The MDP criterion essentially quantifies information in the data the user is prepared to lose in order to gain robustness, where this loss of information (in a loose sense) is represented by the downweighting of data points in the ideal case of the model being correctly specified. Thus the target MDP should be based on the suspected magnitude of any contamination in the response: a harsh contamination can be easily detected thus the target MDP can be set close to 1, resulting in a relatively large value of the tuning constant c, while a subtle contamination requires a smaller MDP, resulting in c being correspondingly smaller.

We empirically confirmed over a variety of models (through simulations not presented here) that the MDP indeed increases monotonically with c until reaching one and remaining constant beyond that. This implies that our new criterion shares a one-to-one relation with the traditional criterion of the ratio of the trace of the asymptotic covariance matrices within the subset of c values that lead to some downweighting under the given design. The MDP is not asymptotic and is in effect tailored to the model and design of the data under study. We finally note that no heavy computation is involved in Step 2: we do not estimate parameters on the simulated $\varvec{y}_b$ vectors, we only need to evaluate the log-likelihood at the true parameter $\hat{\varvec{\delta }}_c$ that generated the sample. In addition, our experience is that Monte Carlo simulation variability is quite small in the MDP so that $B=100$ seems sufficient for most practical purposes.

4 Simulation studies

To investigate the finite sample properties of the proposed estimator, we carry out two simulation studies. In the first one, we assess the robustness properties of our methodology in a GAMLSS setting inspired by the brain imaging data we analyze in Sect. 5. In the second simulation study, we compare our proposal to existing alternatives in the simpler setting of a GAM. All computations are performed in R (R Core Team 2020). Our robust estimator is available in the R package GJRM (Marra and Radice 2020).

4.1 Simulation under a GAMLSS

The data inspiring the GAMLSS simulation design come from functional magnetic resonance imaging (fMRI) of the human brain. These data were presented in Landau et al. (2003) and subsequently used in Wood (2017), and are available in the R package gamair, available on CRAN, as a data frame called brain. The goal of the original study is to test for a difference in the timing (phase shift) of the physiological response between two anatomically distinct brain regions. For this purpose, a set of fMRI measures were acquired from a healthy participant during the performance of a verbal fluency task. The active task of this experiment consisted of generating words beginning with a cued letter, while the baseline condition was given by covertly repeating a letter. Brain activity was then summarized as the median of three measurements of fundamental power quotient on each brain voxel. This physiological activity summary is the nonnegative continuous response variable medFPQ. The coordinates $x_1$ and $x_2$ of each voxel (labeled X and Y, respectively, in the brain data frame in gamair) are used as covariates to model the response surface. The medFPQ measurements roughly range from 0 till 21, with a median around 0.86, and are heavily right-skewed. They are known to be rather noisy with possible spikes and troughs in activity which do not relate to the controlled stimulus (Landau et al. 2003), but the mean response level and its spread are likely to vary smoothly over the 2D brain slice.

In this simulation study, we use the $x_1$ and $x_2$ covariates to generate a response for each voxel according to a GAMLSS with a gamma distribution with expectation $\mu$ and variance $\sigma ^2\mu ^2$ where $\log (\mu ) = \eta _1 = s_1(x_1,x_2)$ and $\log (\sigma ) = \eta _2 = s_2(x_1,x_2)$. The smooth functions $s_1$ and $s_2$ are constructed to mimic the main features of the fitted surfaces on the real data in Sect. 5, see Figure S2 in “Web Appendix C”. The combinations of $x_1$ and $x_2$ values result in a sample size of $n=1567$.

To generate data that is contaminated in a similar way to what is observed in the real data, we modify a clean simulated dataset by choosing at random 78 ($=5\%$) of the responses falling in the upper-right corner of the brain slice, for $x_1 > 70$ and $x_2 > 30$, and by adding 10 to their original value. We simulate 200 replications of the above in both a “clean” scenario (at the assumed model) and in the contaminated scenario. For each replication, we fit a gamma GAMLSS with log links for both $\mu$ and $\sigma$, both with a classical (ML) and with our robust estimation method. We use bivariate thin plate regression splines with k=100 bases to approximate the $s_1$ and $s_2$ smooth functions. Both estimators rely on the EFS method for selecting the smoothing parameters. The robust estimator is tuned to achieve an MDP of 0.95, resulting in $c=3.1$ given the design. We assess estimation performance by investigating the differences between the true parameter and the estimated one, both on the linear predictor scale ($\eta _1$ and $\eta _2$) and on the canonical parameter scale ($\mu$ and $\sigma$), computed as a bias averaged over the n observations. We also compute the mean squared error (MSE) of each target $\theta$ computed as $\text {MSE}(\hat{\theta },\theta ) = \frac{1}{n} \sum _{i=1}^n (\hat{\theta }_i - \theta _i)^2$, where $\theta$ is one of $\eta _1$, $\eta _2$, $\mu$ or $\sigma$.

Figure 1 presents boxplots of the MSE of both methods under both scenarios, while Figure S3 in “Web Appendix C” shows the same but with the vertical scales manually set to improve visualization. Similarly, Figures S4 and S5 present boxplots of MSEs on the scale of $\mu$ and $\sigma$. In “Web Appendix D”, Tables S2 and S3 report summary statistics for the MSE and average bias, respectively. In the clean data scenario, the MSE of classical estimates for both parameters is slightly smaller than that of robust estimates, as theoretically expected. When the data are contaminated, the MSE and average bias of classical estimates explode, whereas the MSE of the robust method only shows a slight increase with somewhat more variability across replications and average bias quite comparable to that with clean data.

Fig. 1

GAMLSS simulation, MSE of the linear predictors $\eta _1$ (left panel) and $\eta _2$ (right panel) for classical and robust methods with data generated at the assumed model and under contamination

We investigate these differences further by looking at the fitted surfaces for $s_1(x_1,x_2)$ and $s_2(x_1,x_2)$. Figure 2 shows colored surfaces representing the average bias across replications $\frac{1}{200}\sum _{j=1}^{200} (\hat{\theta }_{i,j}-\theta _i)$, where $i=1,\ldots ,n$ and $\theta$ is either $\eta _1$ or $\eta _2$, in the clean data scenario; Fig. 3 shows the same under the contaminated scenario. Note that the coloring scales are not the same between the two figures. At the assumed model, we see that both methods perform equally well, showing overall little bias centered about zero. However, under contamination the classical estimates show a large positive bias in the top-right corner of the brain slice, which is precisely the area that is contaminated ($x_1 > 70$ and $x_2 > 30$). Under contamination, the robust estimates show roughly similar biases to those at the model, meaning that the fitted surfaces are quite stable in spite of the contamination. In “Web Appendix C”, Figures S6 and S7 present similar colored surfaces but for $\mu$ and $\sigma$; the results are essentially the same. Overall, this simulation study not only highlights the robustness property of our proposed estimator but also how tuning for an MDP of 0.95 yields smooth functions estimations that are nearly indistinguishable from ML-based ones when the data come from the assumed model.

Fig. 2

GAMLSS simulation, surfaces of the average bias for the linear predictors $\eta _1$ (top row) and $\eta _2$ (bottom row) based on classical (left column) and robust (right column) estimation methods, at the assumed model

Fig. 3

GAMLSS simulation, surfaces of the average bias for the linear predictors $\eta _1$ (top row) and $\eta _2$ (bottom row) based on classical (left column) and robust (right column) estimation methods, under contamination

4.2 Comparison to Robust alternatives in a GAM setting

In order to compare our proposed estimation method to existing robust approaches in the special case of a GAM, we consider here one of the simulation designs of Wong et al. (2014). For $i=1,\ldots ,n$, we generate independent responses $Y_i \sim \text {Poisson}(\mu _i)$ with $\mu _i = \exp (\eta _i)$ and $\eta _i = 4 \cos (2\pi (1 - x_i^2))$, where the $x_i$’s are independently drawn from a $\text {Uniform}(0,1)$ distribution. The sample size is set to $n=100$. Following Wong et al. (2014, p. 280), contaminated data are obtained by randomly selecting 5% or 10% of the original responses and changing them to the nearest integer $y_i u_{1}^{u_2}$, where $u_1$ is drawn from a $\text {Uniform}(2,5)$ distribution and where $u_2$ is randomly set to either 1 or $-1$. We simulate 200 replications.

We compare the following methods, with the same setting choices as in Wong et al. (2014):

• AS: the approach of Alimadad and Salibian-Barrera (2011) with span = 0.5;

• CGP: the approach of Croux et al. (2012) with nknots = 15;

• WYL: the approach of Wong et al. (2014) with $k=30$ basis functions and with smoothing parameter chosen by minimizing their robust BIC, following their recommendation;

• GAMLSS: our proposed approach with $k=20$ basis functions;

• Classical: ML-based estimation with $k=20$ basis functions and smoothing parameter selected by the Fellner–Schall method of Wood and Fasiolo (2017).

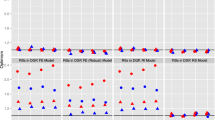
All existing approaches build on Cantoni and Ronchetti (2001b) to define robust penalized estimating equations for $\varvec{\delta }$. Croux et al. (2012) additionally define a similar set of estimating equations for the dispersion parameter in their extended GAM setting. That is, all these approaches robustify estimating (score) equations, typically by appending weights, whereas our proposed approach directly robustifies a likelihood. Regarding smoothers and basis functions, Alimadad and Salibian-Barrera (2011) use local linear fits as smoothers; Croux et al. (2012) use P-splines, while in Wong et al. (2014) the nonparametric fits are based on thin plate regression splines. Regarding the smoothing parameter selection, Alimadad and Salibian-Barrera (2011) use a robust version of CV defined as a sum of squared weighted residuals in line with Cantoni and Ronchetti (2001a), and implemented it in a “brute-force” way; Croux et al. (2012) construct a robust GCV criterion and a robust AIC by applying some bounded function to the deviances appearing in the classical counterparts; while Wong et al. (2014) define robust versions of AIC, BIC and leave-one-out CV, all of them borrowing from the quasi-likelihood definition in Cantoni and Ronchetti (2001b). The proposals based on brute-force (G)CV are generally too demanding to be practical for medium to large applications. The robust information criteria are more tractable, although still with a high computational cost if grid searches are to be used. In all of the three existing approaches, there is no formal treatment of the robustness tuning constant selection. Alimadad and Salibian-Barrera (2011, p. 723) advise to use $c=1.5$, commenting on the fact that “values of c between 1 and 4 produce similar qualitative results”. Croux et al. (2012, p. 33) suggest using $c=1.345$ for both estimating equations for the mean and the dispersion, borrowing from the Gaussian regression setting and stating that “this value gives reasonable results for other models as well”. Finally, Wong et al. (2014) suggest to use $c=1.6$ as in Cantoni and Ronchetti (2001b) without further discussion, even though the simulation designs are different.

Since we only have one smooth term here, we can afford the computational cost of the brute-force CV of AS and consider three variants of our estimator to compare smoothing parameter selection methods: minimizing our proposed robust AIC (RAIC); minimizing our robust BIC (RBIC); and the extended Fellner–Schall method (EFS). The RAIC/RBIC minimizations are performed by a grid search starting from EFS, with a relative numerical tolerance of $10^{-5}$ on the RAIC/RBIC scale. All the methods have been tuned to achieve an MDP of 0.95 following the procedure introduced in Sect. 3.5, to make them comparable. The resulting tuning constants are $k=1.2$ for the AS method, tccM = 1.2 and tccG = 1.345 for CGP, $c=1.2$ for WYL, and $c=5.8$ for our approach. As already noted by Wong et al. (2014, p. 286), the CGP method estimates an additional dispersion parameter by default. This implies greater modeling flexibility and may make the comparison unfair in some situations, but we do not expect this to contribute much to its performance in the simulation settings considered here. We evaluate and compare the performances of the methods by assessing their MSE for the Poisson mean parameter $\mu$ computed as $\text {MSE}(\hat{\mu },\mu ) = \frac{1}{n} \sum _{i=1}^n (\hat{\mu }_i - \mu _i)^2$. The R code for the WYL approach is available through the R package robustGAM, whereas the AS approach is available via the R package rgam. The code for the CGP approach was retrieved from the online supplementary material of Wong et al. (2014).

Figure 4 displays boxplots of the MSE for all methods both at the assumed Poisson GAM model (left sub-panel), under 5% contamination (center sub-panel), and under 10% contamination (right sub-panel). Some summary statistics for the MSE are given in Table 1, while summary statistics for the average bias are reported in Table S4 in “Web Appendix D”. The classical (ML-based) estimation has the lowest MSE under clean data, while it unsurprisingly shows poor performance under contamination. Among the robust methods, AS has the largest MSEs and both AS and WYL tend to vary more across samples than the others. CGP, WYL and our method all roughly have the same MSEs on average, while CGP tends to vary the least under contamination. Among our three variants (RAIC, RBIC and EFS) performance is similar at the model, but under contamination RAIC features slightly larger MSEs than RBIC and EFS. This is in line with remarks made by Wong et al. (2014) about AIC/RAIC favoring wigglier fits which here may allow contaminated observations to contribute relatively more to the fit than with heavier penalties such as BIC/RBIC, and this regardless of the robustness property of the method.

Fig. 4

GAM simulation, MSE at the assumed model and under contaminated data (vertical scale manually set for better visualization, some points not displayed)

Timings for all methods at the model, including the grid searches for minimizing our RAIC/RBIC, are reported in Tables S5 and S6 in “Web Appendix D” (running on a laptop housing a 2.9 GHz CPU). The Classical and CGP usually take less than 1 s and are much faster than the others. Our method with EFS is generally faster than WYL, both of the order of a few seconds, while AS with its brute-force CV is the slowest. Our somewhat crude grid search, with nonetheless strict convergence criteria, generally takes between 1 and 3 min and is usually faster than AS.

Overall, these simulation results yield two main conclusions. First, our proposed robust method performs similarly to the best-performing existing alternatives in the GAM special case. Second, the extended Fellner–Schall method allows for a reliable selection of the smoothing parameter and is on par with minimizing the RBIC but at a fraction of the computational cost of a grid search.

Table 1 GAM simulation, summary statistics of MSE for the robust methods (SD is standard deviation, IQR is inter-quartile range)

5 Application to brain imaging data

In the brain imaging data first presented in Landau et al. (2003), the response variable is the median fundamental power quotient medFPQ which represents the physiological response of the brain to controlled stimuli. This response is measured at voxels in a 2D brain slice with two covariates $x_1$ and $x_2$ identifying the location of each voxel.

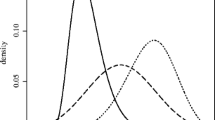
Following Wood (2017), we model both the mean and variance of medFPQ as joint functions $s(x_1,x_2)$ to be approximated by thin plate regression spline basis functions with a smoothness penalty based on second order derivatives. However, contrary to the analysis in Wood (2017, p. 329) where two voxels with medFPQ $\le 5\times 10^{-3}$ were excluded on the ground that they can be regarded as outliers, we will consider the entire data set without exclusions, which amounts to $n=1567$. Given the nonnegative and positively skewed nature of medFPQ, we postulate a gamma distribution parameterized with mean $\mu$ and variance $\sigma ^2\mu ^2$, with $\log (\mu ) = \eta _1 = s_1(x_1,x_2)$ and $\log (\sigma ) = \eta _2 = s_2(x_1,x_2)$. Other families were considered, including the log-logistic distribution which is outside the exponential family; diagnostics and model validation confirmed that a gamma distribution provides the best fit, see Figure S8 in “Web Appendix C”.

We fit the gamma GAMLSS with a classical (ML, non-robust) estimation method and our proposed robust method. Because of the joint smoother used here, we rely on the EFS method which provides fast computations. The robust estimator is tuned to achieve an MDP of 0.95, resulting in a robustness constant of $c=4.5$.

The fitted surfaces for $\eta _1$ and $\eta _2$ are given in Fig. 5. Overall, the robust fitted surfaces appear smoother for both parameters, with a surface that is nearly flat for $\eta _2$. The classical fit uses a total of 77.2 effective degrees of freedom (56.09 for fitting $\eta _1$, 19.11 for $\eta _2$, plus 2 for the constants), whereas the robust fit only uses 30.04 effective degrees of freedom (26.00 for fitting $\eta _1$, 2.04 for $\eta _2$, and 2 for the constants). This hints that the automatic selection of the smoothing parameter in the classical fit was influenced by some potentially outlying observations.

Fig. 5

Brain imaging data, fitted surfaces for the linear predictors $\eta _1$ (top row) and $\eta _2$ (bottom row) based on classical (left column) and robust (right column) estimation methods

Consider the largest local differences in Fig. 5 between the two fits: in the upper-right corner of the brain for $\hat{\eta }_1$ (which has motivated the contamination scheme of Sect. 4.1), and in the leftmost part of the brain for $\hat{\eta }_2$. For the latter, classical estimates imply a much larger localized response variance than robust estimates do. This is driven by two observations in this area which are the ones excluded from the analysis in Wood (2017). Regarding the large differences in $\hat{\eta }_1$ between the two fits, the spike in mean brain activity implied by classical estimates is much subdued when considering robust estimation. This is explained when investigating the robustness weights, which are displayed in Fig. 6. A few observations in the top-right corner are heavily downweighted by the robust method, which results in the smoother mean surface in Fig. 5. These low weights do not imply that these observations are necessarily outliers, but simply that they do not seem to follow the same trends as the majority of the data given the gamma GAMLSS assumed here. The downweighted observations in the top-right corner may indeed represent a physiological response of interest here, we note that the robustness weights identify them in an automated way. Also, note that the two observations excluded by Wood (2017) are also heavily downweighted; these are indicated in Fig. 6 as green crosses for reference. Hence, the robust fitted surfaces combined with the robustness weights are effective at both modeling smooth functions in a reliable way and at automatically detecting observations deviating from trends and model assumptions.

Fig. 6

Brain imaging data, robustness weights from the robust GAMLSS fit, with the two green crosses identifying the two observations excluded from the analysis in Wood (2017). (Color figure online)

6 Discussion

We introduced a robust estimation method for the broad class of GAMLSS. Our approach is quite general since it can be employed for any differentiable likelihood. By directly robustifying the log-likelihood and correcting it for Fisher consistency, this method yields natural robust versions of AIC and BIC. For more complicated designs where grid searches are not feasible, our extended Fellner–Schall method allows for a reliable and automatic selection of smoothing parameters. Our implementation in the R package GJRM, based on the trust region algorithm, is modular and stable. Furthermore, the introduced MDP criterion addresses the challenge of the selection of the robustness tuning constant for models with flexible nonlinear effects in a simple and effective way. We believe this criterion has broad applicability in the implementation of robust methods in many contexts, including the ones where efficiency criteria based on asymptotic covariances already exist but may be computationally expensive.

Simulations in the special case of a GAM showed that our robust estimator is on par with the best-performing existing approaches, when tuned for comparable robustness under the assumed model. Simulations in the broader GAMLSS setting as well as our application to the brain imaging data showed that our robust estimator allows for the automatic detection of deviating observations through the robustness weights, and that the approach yields trustworthy estimates.

The proposed robust estimator has of course some limitations. Like any robust M-estimator, the proportion of contaminated data cannot be unreasonably large without the estimator starting to break at some point (the so-called breakdown point). In our GAM simulations, 10% contamination seems to remain safe for all robust methods given the design but some numerical instabilities do start to arise (notably, our method did diverge on six samples). In a similar fashion, the EFS automated smoothing parameter selection can definitely be improved for numerical stability as it is based on heuristics. Another aspect where more work is needed is in the computation of the Fisher consistency correction term. This term is defined as an integral/sum over the response support, which often needs to be approximated. This approximation can involve heavy computations which may contribute to the numerical stability of the estimator, and ultimately to its reliability. That said, these aspects are not specific to our method, we note that Rigby et al. (2019, p. 259) state in similar way that “Further research is needed on the robust fitting of a GAMLSS model.” Future work also includes the extension to high-dimensional settings, following for instance Mayr et al. (2012) where the problem of variable selection is considered. An alternative strategy for variable selection is developed in Hambuckers et al. (2018) and Groll et al. (2018) using $L_1$-type of penalties.