Greenberger–Horne–Zeilinger state generation with linear optical elements

Abstract

We propose a scheme to probabilistically generate Greenberger–Horne–Zeilinger states encoded on the path degree of freedom of three photons. These photons are totally independent from each other, having no direct interaction during the whole evolution of the protocol, which remarkably requires only linear optical devices to work and two extra ancillary photons to mediate the correlation. The efficacy of the method, which has potential application in distributed quantum computation and multiparty quantum communication, is analyzed in comparison with similar proposals reported in the recent literature. We also discuss the main error sources that limit the efficiency of the protocol in a real experiment and some interesting aspects about the mediator photons in connection with the concept of spatial nonlocality.

Appendix: Calculating the error influence in the protocol of GHZ state generation

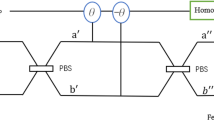
Here we show how to obtain the most general outcome in our protocol of GHZ state generation, as shown in Fig. 1 of the main article. First, one needs to consider all possible paths taken by the photons. At this point, we shall treat each photon independently. For the sake of notation, we divide the interferometer of Fig. 1 into 10 regions (channels), which represents the upper and lower halves of the five circuits. The upper halves of the original circuits of photons 1 to 5 will be labeled as 1, 3, 5, 7, and 9, respectively. On the other hand, the lower halves of these circuits will be labeled as 2, 4, 6, 8, and 10, respectively. For example, the history reflection–reflection–transmission (r,r,t) of photon 1 can be denoted as $(i)^2 R_1|1,1,2\rangle _1$. The parameter $R_{1}$ represents the reflection amplitude of BS$_{1}$, and $i^{2}$ is the phase acquired due to the two reflections.

Note that photons 1 and 5 can have four different histories, whereas photons 2, 3, and 4 can take six different paths before detection. Therefore, the general outcome has $4^2 6^3=3456$ terms. For example, there is a term

$$\begin{aligned} |1,1,2\rangle _1|3,3,3\rangle _2|6,6,5\rangle _3|8,8,7\rangle _4 |10,10,9\rangle _5, \end{aligned}$$

(16)

with coefficient

$$\begin{aligned} i^2 R_1 i^3 R_2 R_6 R_{10} i T_3 R_8 i T_4 R_9 T_{11} T_5 i, \end{aligned}$$

(17)

representing the path (r,r,t); (r,r,r), (t,r,t); (t,r,t) and (t,r,t) of photons 1 to 5, respectively. Again, we put a factor i whenever a reflection takes place, and $R_{j}$ ($T_{j}$) is the reflection (transmission) amplitude of BS$_{j}$. This particular path provides single photons in the channels 2, 3, 5, 7, 9. We denote such outcome as (2, 3, 5, 7, 9), which has the information that photon 1 ends up in channel 2, photon 2 in channel 3, etc. If an experiment had this history, detectors $D_1$ and $D_3$ would click.

Let us consider the following two histories

$$\begin{aligned} |2,2,1\rangle _1|3,3,3\rangle _2|6,7,8\rangle _3|8,8,10\rangle _4 |10,10,9\rangle _5, \end{aligned}$$

(18)

with coefficient

$$\begin{aligned} -i R_6^2 R_2 R_{10} T_1 T_3 T_8 T_{11} T_4 T_9 T_5, \end{aligned}$$

(19)

and

$$\begin{aligned} |2,3,3\rangle _1|3,2,1\rangle _2|6,7,8\rangle _3|8,8,10\rangle _4 |10,10,9\rangle _5, \end{aligned}$$

(20)

with coefficient

$$\begin{aligned} i T_6^2 R_2 R_{10} T_1 T_3 T_8 T_{11} T_4 T_9 T_5. \end{aligned}$$

(21)

The beam splitters in our proposal have $R=T=1/\sqrt{2}$. If the photons are indistinguishable, the above two histories are equivalent. Due to the opposite sign in the linear combination, this term does not have any contribution at the end (the HOM effect at BS$_6$ with the simultaneously arrivals of photons 1 and 2). One can handle the failure of the HOM effect at the second layer by keeping the photons distinguishable, but changing $R_i^2=T_i^2=\delta$ for $i=6\dots 9$ in the coefficients, and then setting the remaining factors $R_i$ and $T_i$ to $1/\sqrt{2}$ (50:50 beam splitters and allowed failure of the HOM effect with probability $\delta$). When $\delta =0$, we have the ideal case considered in the main text.

Having the above substitutions been carried out, one can apply detector projections. Here we suppose that the detectors can count the number of incoming photons. To get the GHZ state ($|\psi \rangle _1$), for example, one needs exactly one click on the detectors $D_1$ and $D_3$ and no click on the other two detectors (postselection). Therefore, from the general linear combination of the outgoing state, one can select only the ones which have exactly one photon in channels 3 and 7 and no photons in channels 4 and 8.

As a matter of fact, we can restore the indistinguishability of the photons by checking the last parts of the history and identifying the indistinguishable outcomes. For example, one identifies (1, 3, 8, 10, 9) with (3, 1, 8, 10, 9). See the HOM failure example above. Then, one has to sum up over all the possible histories generating the same outcome. With $\delta =0$, the $D_1D_3$ postselection leads to the following general outcome:

$$\begin{aligned} |\psi (\delta =0)\rangle _{1,gen}= & {} \frac{1}{64} i |1\rangle _1 |1\rangle _2 |5\rangle _4+\frac{1}{64} i |1\rangle _1 |5\rangle _3 |5\rangle _4+\frac{1}{64} |6\rangle _2 |5\rangle _3 |5\rangle _4 \nonumber \\&+\,\frac{i |2\rangle _1 |6\rangle _3 |5\rangle _4}{32 \sqrt{2}}+\frac{1}{64} i |6\rangle _2 |6\rangle _3 |5\rangle _4-\frac{|2\rangle _1 |1\rangle _2 |5\rangle _4}{32 \sqrt{2}} \nonumber \\&+\,\frac{i |1\rangle _1 |5\rangle _3 |9\rangle _5}{32 \sqrt{2}}+\frac{|6\rangle _2 |5\rangle _3 |9\rangle _5}{32 \sqrt{2}}+\frac{|1\rangle _1 |10\rangle _4 |9\rangle _5}{32 \sqrt{2}} \nonumber \\&+\,\frac{1}{64} |1\rangle _1 |1\rangle _2 |10\rangle _5+\frac{i |2\rangle _1 |1\rangle _2 |10\rangle _5}{32 \sqrt{2}}+\frac{|2\rangle _1 |6\rangle _3 |10\rangle _5}{32 \sqrt{2}} \nonumber \\&+\,\frac{1}{64} |6\rangle _2 |6\rangle _3 |10\rangle _5+\frac{1}{64} i |1\rangle _1 |10\rangle _4 |10\rangle _5 \nonumber \\&+\,\frac{1}{64} |6\rangle _2 |10\rangle _4 |10\rangle _5-\frac{i |6\rangle _2 |9\rangle _5 |10\rangle _4}{32 \sqrt{2}}. \end{aligned}$$

(22)

If $\delta \ne 0$, one has even more terms. One can easily see that there are many outcomes with multiple photons in the same channel.

Let us suppose that one can make an extra postselection step, namely selecting outcomes with single photons in each channel (for example, by using at the end an apparatus which works only with single-photon input states). In this case, the general ($\delta \ne 0$) outcome is the following

$$\begin{aligned}&\frac{i \left( 1-2 \sqrt{\delta }\right) ^2 |1\rangle _1 |5\rangle _3 |9\rangle _5}{32 \sqrt{2}}+\frac{\left( 1-2 \sqrt{\delta }\right) ^2 |2\rangle _1 |6\rangle _3 |10\rangle _5}{32 \sqrt{2}} \nonumber \\&+\,\frac{1}{32} \sqrt{\delta } \left( 1-2 \sqrt{\delta }\right) |1\rangle _1 |5\rangle _3 |10\rangle _4+\frac{\sqrt{\delta } \left( 1-2 \sqrt{\delta }\right) |2\rangle _1 |6\rangle _3 |10\rangle _4}{16 \sqrt{2}} \nonumber \\&+\frac{\sqrt{\delta } \left( 1-2 \sqrt{\delta }\right) |2\rangle _1 |6\rangle _2 |10\rangle _5}{16 \sqrt{2}}+\frac{i \delta |1\rangle _2 |5\rangle _4 |9\rangle _5}{8 \sqrt{2}} \nonumber \\&+\,\frac{1}{16} \delta |1\rangle _2 |5\rangle _3 |10\rangle _4+\frac{1}{16} \delta \left( \sqrt{2} |2\rangle _1-i |1\rangle _1\right) |6\rangle _2 |10\rangle _4 \nonumber \\&+\,\frac{1}{16} i \delta |1\rangle _2 |6\rangle _3 |10\rangle _4+\frac{1}{32} \left( 2 \sqrt{\delta }-1\right) \sqrt{\delta } |1\rangle _1 |5\rangle _4 |10\rangle _5 \nonumber \\&-\,\frac{1}{16} \delta |1\rangle _2 |5\rangle _4 |10\rangle _5+\frac{1}{32} i \left( 2 \sqrt{\delta }-1\right) \sqrt{\delta } |1\rangle _1 |6\rangle _2 |10\rangle _5 \nonumber \\&-\,\frac{1}{32} i \left( 2 \sqrt{\delta }-1\right) \sqrt{\delta } |1\rangle _2 |6\rangle _3 |10\rangle _5-\frac{i \left( 2 \sqrt{\delta }-1\right) \sqrt{\delta } |1\rangle _2 |5\rangle _3 |9\rangle _5}{16 \sqrt{2}} \nonumber \\&-\,\frac{i \left( 2 \sqrt{\delta }-1\right) \sqrt{\delta } |1\rangle _1 |5\rangle _4 |9\rangle _5}{16 \sqrt{2}}. \end{aligned}$$

(23)

It is easy to see that the GHZ state is obtained when $\delta =0$

$$\begin{aligned} \frac{|2\rangle _1 |6\rangle _3 |10\rangle _5}{32 \sqrt{2}}+\frac{i |1\rangle _1 |5\rangle _3 |9\rangle _5}{32 \sqrt{2}} \end{aligned}$$

(24)

or restoring the notation of Sect. 2 in the main text

$$\begin{aligned} \frac{|B\rangle _1 |B\rangle _3 |B\rangle _5}{32 \sqrt{2}}+\frac{i |A\rangle _1 |A\rangle _3 |A\rangle _5}{32 \sqrt{2}}. \end{aligned}$$

(25)