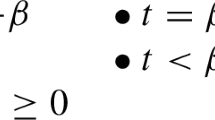Indicative conditionals: probabilities and relevance

People do not consider the conditional probability to be the only basis for asserting a conditional, even if they judge the probability of the conditional to be the conditional probability.

Evans & Over, If.

Abstract

We propose a new account of indicative conditionals, giving acceptability and logical closure conditions for them. We start from Adams’ Thesis: the claim that the acceptability of a simple indicative equals the corresponding conditional probability. The Thesis is widely endorsed, but arguably false and refuted by empirical research. To fix it, we submit, we need a relevance constraint: we accept a simple conditional $\varphi \rightarrow \psi$ to the extent that (i) the conditional probability $\mathrm{p}(\psi |\varphi )$ is high, provided that (ii) $\varphi$ is relevant for $\psi$. How (i) should work is well-understood. It is (ii) that holds the key to improve our understanding of conditionals. Our account has (i) a probabilistic component, using Popper functions; (ii) a relevance component, given via an algebraic structure of topics or subject matters. We present a probabilistic logic for simple indicatives, and argue that its (in)validities are both theoretically desirable and in line with empirical results on how people reason with conditionals.

1 Adams’ thesis and the problem of relevance

Adams’ Thesis (Adams 1966, 1975) has it that the acceptability of a simple indicative conditional $\varphi \rightarrow \psi$—an indicative with no indicatives in $\varphi$ or in $\psi$—equals the corresponding conditional probability:

(AT):

$Acc(\varphi \rightarrow \psi ) = \mathrm{p}(\psi | \varphi )$

Stalnaker’s Hypothesis (Stalnaker 1975), also called the Equation, has it that the probability of an indicative $\varphi \rightarrow \psi$ equals its conditional probability:

(SH):

$\mathrm{p}(\varphi \rightarrow \psi ) = \mathrm{p}(\psi | \varphi )$¹

AT is popular in philosophy among proponents of the non-propositional view of indicatives (Edgington 1995; Adams 1998; Bennett 2003). SH is popular in psychology: it is in line with the New Paradigm Psychology of Reasoning (Over 2009; Elqayam and Over 2013), which puts probabilities at center stage in the study of reasoning, and handles conditionals probabilistically (Evans and Over 2004; Oaksford and Chater 2010). The Paradigm is becoming so dominant that even proponents of essentially non-probabilistic accounts of the conditional, like the mental models theory (Johnson-Laird and Byrne 2002), feel the need to relate their view to probabilities (Girotto and Johnson-Laird 2010).

However, Lewis’ and others’ notorious triviality results (Lewis 1976; Hajek 1989) are often taken as showing that SH can’t be quite right. On the other hand, by endorsing AT rather than SH, non-propositionalists can insist that indicatives be handled probabilistically: they are safe from triviality for they don’t express propositions and cannot generally be embedded (hence the limitation to simple conditionals in AT).² They generally lack truth values,³ thus probabilities of truth properly so called, as Adams realized. But they can have acceptability conditions, as per AT. McGee (1986) claims that ‘[AT] describes what English speakers assert and accept with unfailing accuracy’ (485). And Jackson:

There is a great deal of evidence for [AT]. There is head-counting evidence. Very many philosophers of otherwise differing opinions have found [AT] highly intuitive. There is case-by-case evidence. Take a conditional which is highly assertible [...]; it will invariably be one whose consequent is highly probable given its antecedent. (Jackson 1987, p. 12)

But AT is false. A conditional probability $\mathrm{p}(\psi | \varphi )$ for an unacceptable indicative can be high because $\psi$ is already likely and has little to do with $\varphi$:

• 1. If Brexit causes a recession, then Jupiter is a planet.

One may claim that (1) is unacceptable for its consequent has probability 1. We’ll come back to the issue of conditionals with extreme antecedent or consequent probabilities. Even granting the claim, sometimes conditionals with high but less than 1 probability of their consequent are unacceptable because this has little to do with their antecedent:

• 2. If Brexit causes a recession, then there will be some heads in the first 100 tosses of this fair coin.

AT is empirically inadequate.⁴ In the experiments reported in Douven and Verbrugge (2010), one group of subjects was given contexts $C_i$, $1 \le i \le 30$, and asked to rate the acceptability of conditionals $\varphi _i \rightarrow \psi _i$ in $C_i$. Another group was given the same contexts $C_i$ and asked to judge the probability of $\psi _i$ in $C_i$ on the supposition that $\varphi _i$. People’s patterns of (degrees of) acceptance for conditionals generally don’t even approximate the corresponding conditional probabilities: this ‘manifestly refute[s] Adams’ Thesis, both in its strict form AT and in its approximate form’ (Douven 2016, p. 99).⁵

What’s wrong with AT? Compare (2) above with the following, adapting (Douven 2016, p. 104):

• 3. If there’s some heads in the first 10 tosses, then there will be some heads in the first 100 tosses of this fair coin.

We accept (3), not (2), because (3)’s antecedent is relevant for the consequent, which is, instead, off-topic with respect to (2)’s antecedent. This suggests a fixing for AT: we accept a conditional to the extent that (i) the consequent is likely conditional on the antecedent, provided (ii) some relevance or topicality connection linking antecedent and consequent is satisfied. How (i) should work is well-understood already. It is (ii) that holds, we submit, the key to improve our understanding of conditionals.

What is relevance or topicality for indicatives? A venerable idea going back to Grice (1989), and sometimes invoked to save the material conditional analysis from apparent counterexamples, is that it’s a pragmatic issue: some perfectly true or probabilistically all right conditionals are unassertable, lacking a connection between antecedent and consequent:⁶ see e.g. (Johnson-Laird and Byrne 1991, p. 8). But we shouldn’t take for granted that relevance has to be handled merely as pragmatic coherence. Sophisticated approaches to the logic of conditionals, such as relevance logics (Dunn and Restall 2002), make relevance amenable to a rigorous, compositional, and properly semantic treatment, and have also been developed for ceteris paribus conditionals (Mares and Fuhrmann 1995; Mares 2004). Besides, as Krzyżanowska et al. (2017) have shown, pragmatic discourse coherence is a weaker constraint than proper relevance of conditional antecedents for their consequents: the former only requires not to assert a conjunction when the two conjuncts have nothing to do with each other in the given conversational context (‘Brexit will cause a recession and Jupiter is a planet’ is an odd thing to say in one breath, in natural conversational contexts where what happens after Brexit, and what kind of thing Jupiter is, are completely disconnected topics). However, sometimes a conjunction is assertable in a given context because of some topic overlap between the two conjuncts, but we don’t want to assert the corresponding conditional in the very same context. Picking Krzyżanowska et al.’s own example, one can easily think of contexts where this is clearly assertable:

• 4. Raccoons have no wings and they cannot breath under water.

What makes (4) pragmatically all right is that the two conjuncts overlap in topic—both are about raccoons, although they say disparate things about them. But we may not want to assert, in the very same contexts in which (4) is a fine thing to say, the corresponding conditional:

• 5. If Raccoons have no wings, then they cannot breath under water.

Or suppose this (now drawing on Priest (2008, p. 96)) is true:

• 6. A fortune-teller predicts that you’ll win the lottery, and you do.

It’s pragmatically all right to assert (5) in a number of contexts, for its conjuncts overlap in topic, both having to do with your winning the lottery. But we may not want to assert, in those same contexts, the corresponding superstitious conditional:

• 7. If a fortune-teller predicts that you’ll win the lottery, then you do.

Krzyżanowska et al. (2017) exhibit experimental results showing that, even when people find it pragmatically appropriate to assert conjunctions like (4) or (6), they tend not to assert the corresponding irrelevant conditionals, (5) and (7).⁷

The moves from (4) to (5), or from (6) to (7), are instances of the And-to-If schema, licensing the inference from a conjunction to the corresponding conditional:

(And-to-If):

$\varphi \wedge \psi \vDash \varphi \rightarrow \psi$⁸

And-to-If is sometimes called ‘Centering’, for it holds in the mainstream similarity-based possible worlds semantics for conditionals due to Stalnaker (1968) and Lewis (1973) (Lewis advertised it for subjunctives or counterfactuals, however, not indicatives), when one assumes that the world of evaluation is always the single world most similar to itself (it’s the unique one at the center of the nested spheres of worlds arranged around it, more similar worlds inhabiting smaller spheres). It doesn’t hold only there. A number of mainstream theories of indicatives validate And-to-If: the material conditional view (Jackson 1987; Grice 1989) and the probabilistic-suppositional view (Adams 1975; Edgington 1995; Evans and Over 2004), for instance, have it. They shouldn’t: a true, acceptable conjunction doesn’t generally warrant the truth, or acceptability, of the corresponding conditional, and the mismatch between the two is not easily reducible to the pragmatics of discourse coherence.

Two theories of indicatives, however, naturally invalidate And-to-If. Their discussion in Sect. 2 will make a number of useful points emerge, in view of the presentation of our own account starting in Sect. 3.

2 Inferentialism and evidential support

Some inferentialist (Braine 1978; Braine and O’Brien 1991) approaches to conditionals have it that conditionals express enthymematic arguments.⁹ The idea goes back to Mill’s System of Logic, and was endorsed by Ramsey in the same work where he introduced (what we now call) his ‘test’, whereby we evaluate a conditional by supposing the antecedent and assessing the consequent under that supposition:¹⁰

[W]e can say with Mill that ‘If p, then q’ means that q is inferrible from p, that is, of course, from p together with certain facts and laws not stated but in some way indicated by the context. (Ramsey 1990, p. 156)

So $\varphi \rightarrow \psi$ says that there’s some good inference from $\varphi$ and background assumptions (‘facts and laws’) $BA_\varphi$ to $\psi$. Besides plausibly depending on the antecedent (that’s what the subscript is there for), background assumptions depend on context and their list can be open-ended. They capture the idea that everyday conditionals are for the most ceteris paribus and non-monotonic: ‘If the weather is good, I’m going to play golf’ doesn’t imply ‘If the weather is good and I break my ankle, I’m going to play golf’. (Different approaches capture ceteris paribus features in different ways, e.g., variable strictness does it in the Lewis–Stalnaker semantics.)

For lots of good conditionals, there is no way to deduce $\psi$ from $\varphi$, no matter what $BA_\varphi$ come to help. But we needn’t assume that the valid inference at issue be deductive: $\psi$ may follow from $\varphi$ and $BA_\varphi$ also inductively, abductively, or via a mixture of different ways of inferring. Krzyzanowksa (2015, pp. 64–5) imposes constraints on the connection between premises and conclusion which ensure that $\psi$ doesn’t follow trivially from $\varphi$ and $BA_\varphi$, thus capturing a kind of relevance. The view makes And-to-If fail in a most natural way: the mere fact that $\varphi$ and $\psi$ are true together doesn’t warrant there being a good argument from the former (and, $BA_\varphi$) to the latter.

Inferentialism (of this kind) has not been proposed, as far as we know, as a general account of indicatives. It can hardly be one. Linguists distinguish inferential from content conditionals (Declerck and Reed 2001; Haegeman 2003; Dancygier and Sweetser 2005) expressing non-logical connections between states of affairs: ‘If John passes the exam, we’ll have a party’; ‘She’s such a disappointment if she thinks so highly of him’. As stressed by Douven, the connections between antecedent and consequent in relevant conditionals can be of the most diverse kinds:

[C]onditionals have been said to require for their truth the presence of a ‘connection’ linking their antecedent and consequent. Proposals in this vein immediately raise the question of what the nature of the supposed connection could be. Candidate answers abound: it could be logical, statistical, causal, explanatory, metaphysical, epistemic; or the ‘connector’ could be a second-order functional property, notably, the property that there is some first-order property or other that links antecedent and consequent. (Douven 2016, pp. 35–6)

It’s dubious that all relevant conditionals express the existence of some argument from their antecedent and contextually determined background assumptions to their consequent. It is surely in agreement with the Ramsey test to say that their assessment always involves some form of mental simulation, whereby we assess the consequent under the supposition of the antecedent. To label the process ‘inferential’ in all cases just on this basis, however, would be to stretch the term beyond usefulness: surely any conditional trivially says that its consequent follows, in some sense or other, from its antecedent. A general account of indicatives calls for a general notion of relevance. The criterion of relevance proposed in our account below aims at giving a catch-all condition, covering relevance of any kind, whether inferential or not.

Next, whenever an argument condensed in $\varphi \rightarrow \psi$ is not purely deductive, it may be valid even when $\varphi$ is true and $\psi$ isn’t: good arguments involving inductive or abductive steps may fail to be necessarily truth-preserving. Thus, inferentialism is bound to invalidate Modus Ponens (Krzyżanowska 2015, pp. 70–1). But preserving X forwards (X being truth, or degrees of probability, of acceptability, or whatnot) has often been taken as a minimal requirement for an operator to count as a conditional. Putative exceptions are very controversial, and anyway involve peculiar sentences (paradoxes like the Liar, see Beall (2015)), or contexts like the famous McGee cases—which anyway don’t affect simple conditionals, as they crucially involve right-nested ones. As McGee himself admitted, ‘there is every reason to suppose that, restricted to [simple] conditionals, modus ponens is unexceptionable’ (McGee 1985, p. 468). Additionally, with over 97% endorsement across a range of empirical tests (Oaksford 2005; Oaksford and Chater 2010), Modus Ponens is by far the most popular inference involving conditionals and one of the most popular tout-court (Evans and Over 2004, pp. 46–52). Admittedly (as suggested by an anonymous referee) the inferentialist can make sense of this by claiming that Modus Ponens is highly reliable, to the extent that the relevant non-deductive inferences are, and this is enough to explain both our intuitions about it and the high endorsement rate in various experiments.

The evidential support thesis (EST) championed by Douven (2016) proposes to fix AT by adding to it a relevance condition of evidential support. Evidence is understood probabilistically: $\varphi$ is evidence for $\psi$ by making it more likely.¹¹ The qualitative (non-graded) acceptability conditions for a simple indicative are:

(EST):

$\varphi \rightarrow \psi$ is acceptable iff (i) $\mathrm{p}(\psi | \varphi ) > \theta$ and (ii) $\mathrm{p}(\psi | \varphi ) > \mathrm{p}(\psi )$

(i) is a qualitative variant of AT, saying that the conditional probability passes a threshold (say, $\theta \in [0.5, 1)$). (ii) is the evidential constraint: $\psi$ is more likely conditional on $\varphi$ than it is unconditionally. And-to-If nicely fails: $\varphi \wedge \psi$ can be true and acceptable without $\varphi$ raising one bit the probability of $\psi$. This seems to be what is going on in a number of cases where we don’t accept a conditional with true antecedent and consequent.

One issue with the view is its inferential weakness. Douven defines a notion of logical consequence as acceptability-preservation: when all premises reach a threshold of acceptability $\theta$, the conclusion does, too. An inference is valid for t when it’s acceptability-preserving for $\theta = t$, invalid for t otherwise. An inference is valid (invalid) simpliciter when valid (invalid) for all $t \in [0.5, 1)$ (Douven 2016, p. 130). When ‘$\vDash$’ is such validity, we have the following failures for the EST conditional:¹²

(Modus Ponens):

$\varphi \rightarrow \psi , \varphi \nvDash \psi$

(CC):

$\varphi \rightarrow \psi , \varphi \rightarrow \chi \nvDash \varphi \rightarrow (\psi \wedge \chi )$ (Conjunction in the Consequent)

(CMon):

$\varphi \rightarrow \psi , \varphi \rightarrow \chi \nvDash (\varphi \wedge \psi ) \rightarrow \chi$ (Cautious Monotonicity)

(CT):

$\varphi \rightarrow \psi , (\varphi \wedge \psi ) \rightarrow \chi \nvDash \varphi \rightarrow \chi$ (Cautious Transitivity)¹³

We’ve already highlighted the badness of Modus Ponens failure. Segerberg (1989) claims that CC should hold in any reasonable system of conditional logic.¹⁴ There is wide agreement on CMon and CT, too, being required in a good conditional logic. Both feature in Chellas (1975)’s basic conditional logic. The basic system of non-monotonic entailment C in the seminal Kraus et al. (1990) has CMon and CT, which according to Gabbay (1985), are two minimal inferental schemata any non-monotonic notion of entailment must comply with. The popular non-monotonic logic P of preferential models by Kraus et al. (1990) has them, too. It has been claimed that such principles are both theoretically and empirically desirable (Pfeifer and Kleiter 2010): they are strong enough to do the job of the invalid unrestricted monotonicity (from $\varphi \rightarrow \psi$ to $\varphi \wedge \chi \rightarrow \psi$) and transitivity (from $\varphi \rightarrow \psi$ and $\psi \rightarrow \chi$ to $\varphi \rightarrow \chi$) in most cases, while helping to explain why people sometimes endorse the latter by over-generalizing—as argued, among many, by Adams (1975), Bennett (2003), Pfeifer and Kleiter (2010).

The inferential weakness of EST may be tied to the particular way in which Douven defines his probabilistic logic.¹⁵ But one issue besets the view due to its understanding relevance as probabilistic evidence: EST does not fare well with extreme probabilities. If $\mathrm{p}(\varphi ) = 0$, $\varphi$ can hardly be evidence for anything. If $\mathrm{p}(\psi ) = 1$, nothing can raise the probability of $\psi$. Then any conditional $\varphi \rightarrow \psi$ with 0 antecedent-probability or 1 consequent-probability is unacceptable. Many such conditionals, however (the relevant ones!), sound perfectly acceptable in a number of contexts. Douven (2016, p. 113) discusses one example of relevant conditional whose consequent has probability 1:

• 8. If Obama is president of the United States, his residence is in the White House.

While he finds (8) odd, we can think of a number of contexts in which it would be perfectly acceptable.¹⁶ If this can be done for a conditional like (8), whose antecedent and consequent are both not only true (at the time of Douven’s writing), but also widely shared knowledge, it should’t be too difficult to find such contexts for a number of probability 1 consequents.

The case of 0 probability antecedents, anyway, is more telling. Pace Bennett (2003) and others, one can non-trivially assess, and reason with, indicatives whose antecedent one fully takes to be false. One is pretty sure that Oswald killed Kennedy but has no troubles assessing ‘If Oswald did not kill Kennedy, then someone else did’ (Gillies 2004). As stressed by Joyce (1999), unpretentious thinkers can suppose in the indicative mood that $\varphi$ also when they utterly disbelieve $\varphi$, and assess whether $\psi$ is the case under that supposition:

[I]t is often assumed that any form of probabilistic belief revision that involves ‘raising the dead’ by increasing the probabilities of certainly false propositions must involve counterfactual beliefs. This is not so. It is logically consistent both to be certain that some proposition is false and yet to speculate about what the world is like if one is in fact wrong. To be subjectively certain of something is, after all, not the same as regarding oneself infallible on the matter. (Joyce 1999, p. 203)

This holds even for conditionals whose antecedents are taken as necessarily false:

• 9. If all even numbers are prime and 5 is even, then 5 is prime.

• 10. If all even numbers are prime and 5 is even, then one cannot square the circle.

(9) seems perfectly acceptable although its antecedent is a necessary falsity. Its same-antecedent (10) doesn’t look acceptable – because a relevant connection with the consequent is missing. Douven mentions that these cases could be handled by resorting to a non-standard probabilistic account that doesn’t assign probability 0 to all logical and mathematical falsehoods (Douven 2016, p. 114). The issue with (9), though, is that it seems to be acceptable also for one who is certain that its antecedent is false.

Cases like (9) and (10) give some evidence for a point at times neglected in the literature: conditionals are hyperintensional, at least as far as their acceptability conditions go.¹⁷ We sometimes have different attitudes towards conditionals whose antecedents and, respectively, consequents, are necessarily equivalent, having the same truth value across all possible worlds: we accept the relevant ones, not the irrelevant ones. The account we propose below makes conditionals hyperintensional precisely in this way.¹⁸

The so-called Ratio Formula, which defines a conditional probability $\mathrm{p}(\psi | \varphi )$ as the ratio of two unconditional probabilities $\mathrm{p}(\varphi \wedge \psi ) / \mathrm{p}(\varphi )$, makes a conditional probability undefined for $\mathrm{p}(\varphi ) = 0$. This should be taken as a problem for a treatment of conditionals that resorts to it, rather than for the claim that one can non-trivially reason with, or assess, indicatives with zero antecedent-probability. The use of Popper functions, whereby one doesn’t define conditional probabilities via unconditional ones, is often recommended because they easily handle such cases. Several approaches to conditional belief and belief revision (e.g. Van Fraassen (1995), Arlo-Costa and Parikh (2005), Baltag and Smets (2008)), thus, endorse an extension of classical probability theory using Popper functions. We are doing the same for our account.

3 Topicology

We need a relevance constraint to fix AT: we accept $\varphi \rightarrow \psi$ to the extent that (i) $\mathrm{p}(\psi | \varphi )$ is high, provided (ii) $\varphi$ is relevant for $\psi$. Unlike EST, we understand relevance in (ii) as topic-sensitivity: a relevant conditional is one whose consequent is about the right topic, as contextually determined by its antecedent. We thus need to say what aboutness and topics are.

Aboutness, as Yablo has it, is ‘the relation that meaningful items bear to whatever it is that they are on or of or that they address or concern’ (Yablo 2014, p. 1): this is their topic, or subject matter. Work on aboutness has been burgeoning among philosophers (Putnam 1958; Goodman 1961; Lewis 1988; Plebani and Spolaore 2020), linguists (Roberts 2011), and logicians (Fine 1986; Humberstone 2008; Fine 2017; Berto and Hawke 2018; Berto 2019; Özgün and Berto 2020). Declarative sentences are used to say true things about all kinds of topics. One says: ‘John is a plumber’. One thereby communicates something about John’s profession and, more generally, John. What one says is true just in case John’s profession includes being a plumber. One addresses certain topics and says that things are such-and-so with respect to them.

Topics are naturally linked to questions or issues under discussion in a discourse context (Lewis 1988; Roberts 2012): ‘Our topic today is whether Brexit will cause a recession’ maps to ‘Will Brexit cause a recession?’. Topics needn’t be framed as questions (‘Our topic is the number of stars’), but there will always be a question in the vicinity (‘How many stars are there?’). Thus, Lewis (1988) took topics as partitions of the set of possible worlds: the topic the number of stars is the partition determined by the question, ‘How many stars are there?’. Worlds end up in the same cell when they agree on the answer: all zero-star worlds end up in one cell, all one-star worlds in another, and so on. Others have understood topics as sets or fusions of a sentence’s truthmakers or falsemakers (Fine 2016, 2017; Fine and Jago 2018), taken in their turn as states or situations à la Barwise and Perry (1983), which, unlike possible worlds, can fail to be maximal or consistent.

We don’t need to take a stance on the exact nature of topics, however: for our purposes, we only need them to obey three constraints. These are widely agreed upon in subject matter semantics:

• (1) Logically or necessarily equivalent sentences $\varphi$ and $\psi$ can differ in content when they are about different things. In Yablo (2014)’s version, for instance, the propositional content of a sentence (in context) is not specified just by the set of worlds in which it is true (‘proposition’ in the UCLA sense of Montague–Lewis–Stalnaker-etc.), but also by what it’s about. Subject matter semantics is, thus, hyperintensional, making distinctions more fine-grained than what standard intensional (possible worlds) semantics allows: ‘2 + 2 = 4’ and ‘Either Jupiter is a planet, or not’ differ in content in spite of being true at the same worlds (all of them), for they say different things: only one is about the number 2.

• (2) The space of topics must have a mereological structure (Yablo 2014; Fine 2016): topics can have proper parts; distinct topics may have common parts; and one topic may be included in another in that every part of the former is also a part of the latter. Mathematics includes arithmetic. Mathematics and philosophy overlap, having (certain parts of) logic as a common part. This reflects on notions of same-saying, saying more, saying less for the contents of assertions. Plausibly the topic of $\varphi \wedge \psi$ includes that of $\varphi$ as a (proper) part; so if Mary says ‘Obama is tall and handsome’ and John says ‘Obama is tall’, what John said has already been said by Mary—who also said more: John has addressed a topic, say Obama’s height, which is a (proper) part of the larger topic addressed by Mary, the height and looks of Obama’s. Plausibly, the topic of $\varphi \wedge \psi$ is the same as that of $\psi \wedge \varphi$ when ‘$\wedge$’ represents commutative, order-insensitive Boolean conjunction. So if Mary says ‘Obama is tall and handsome’, and John says ‘Obama is handsome and tall’, they have said the same thing.¹⁹

• (3) A third point of agreement (Perry 1989; Yablo 2014; Fine 2016) is that the Boolean logical operators should add no subject matter of their own: they are ‘topic-transparent’. The topic of $\lnot \varphi$ is the same as that of $\varphi$ (‘Obama is not tall’ is exactly about what ‘Obama is tall’ is about—Obama’s height; it certainly is not about not).²⁰ Conjunction and disjunction merge topics (‘Obama is tall and handsome’ and ‘Obama is tall or handsome’ are both about the same topic: the height and looks of Obama’s). Transparency accommodates the venerable idea that the laws of logic are formal in the sense of being topic-neutral, or subject-matter-independent.

Here’s what we are going to do next. In Sect. 4, we will introduce a propositional formal language including a simple indicative conditional, for which we are giving acceptability conditions in terms of probabilities and topics. In Sect. 5, we’ll then define a notion of logical consequence in terms of preservation of degrees of (un)acceptability from premises to conclusion. We’ll show that our conditional has logical closure properties which are not only intuitively plausible, but also mirror people’s empirical judgments on a number of inferences involving indicatives.

We will focus on simple indicatives and give only graded acceptability conditions for them, not truth conditions, to accommodate non-propositionalist views. We want to be able to conditionalize on 0 probabilities in a non-trivial way. We will therefore use Popper functions, following Hawthorne (1996) and Leitgeb (2012), among others. We interpret the conditional probability measures subjectively-epistemically, not as objective frequencies, following the mainstream on indicatives (Adams 1966, 1975, 1998; McGee 1986; Douven 2016).

4 A topic-sensitive, probabilistic semantics

Here is our core idea: the degree of acceptability of a simple indicative $\varphi \rightarrow \psi$ is given, (i) as per AT, by the corresponding conditional probability, ${\mathcal {P}}(\psi | \varphi )$, provided (ii) the conditional is on-topic—otherwise, $\varphi \rightarrow \psi$ has zero acceptability. A conditional is on-topic when the topic of its consequent is fully included in a topic contextually determined by its antecedent. Arguably, this latter is not just the topic of the antecedent $\varphi$. Rather, it is the topic of the relevant background assumptions $BA_\varphi$ determined by $\varphi$ and context (where, plausibly, $\varphi \in BA_\varphi$). That’s because we sometimes accept $\varphi \rightarrow \psi$ without direct topic-inclusion between $\varphi$ and $\psi$:

• 11. If we keep burning fossil fuels at this pace, the polar ice will melt.

• 12. If Brexit causes a recession, the Tories won’t win the next election.

• 13. If you push the button, the engine will start.

In cases like (11)-(13), the antecedent is relevant for the consequent although it doesn’t, on its own, address an issue with respect to which the consequent is fully on-topic. Rather, the supposition of the antecedent triggers, in context, background assumptions with respect to which the consequent is fully on-topic (e.g., for (11), fossil fuel burning triggers topics such as the emission of CO₂, raising global temperatures, etc.). The topicality is between the background $BA_\varphi$ and $\psi$.²¹ The topic of $BA_\varphi$ is determined, given that of $\varphi$, by a function f obeying plausible constraints.

Let ${\mathcal {L}}_{PL}$ denote the language of classical propositional logic defined on a countable set of propositional variables ${\mathsf {Prop}}=\{p, q, \dots \}$ with connectives $\lnot$ and $\wedge$. The well-formed formulas are the elements of ${\mathsf {Prop}}$, $\lnot \varphi$, and $(\varphi \wedge \psi )$ whenever $\varphi$ and $\psi$ are formulas. We identify ${\mathcal {L}}_{PL}$ with the set of its well-formed formulas and employ the usual abbreviations for propositional connectives $\vee , \supset , \equiv$ as $\varphi \vee \psi :=\lnot (\lnot \varphi \wedge \lnot \psi )$, $\varphi \supset \psi := (\lnot \varphi \vee \psi )$, and $\varphi \equiv \psi := (\varphi \supset \psi ) \wedge (\psi \supset \varphi )$. So, $\supset$ is the material conditional and $\equiv$ is the material biconditional. As for $\top$ and $\bot$, we set $\top :=p\vee \lnot p$ and $\bot :=\lnot \top$. We call the elements of ${\mathcal {L}}_{PL}$ Boolean sentences. For any $\varphi \in {\mathcal {L}}_{PL}$, ${\mathsf {P}}_\varphi$ denotes the set of propositional variables occurring in $\varphi$. We use the symbol $\vDash _{PL}$ for classical logical truth/consequence.

The full language ${\mathcal {L}}$ of simple indicative conditionals extends ${\mathcal {L}}_{PL}$ by an indicative conditional operator $\rightarrow$, which connects only the elements of ${\mathcal {L}}_{PL}$. The well-formed formulas in ${\mathcal {L}}$ are the elements of ${\mathcal {L}}_{PL}$ and $(\varphi \rightarrow \psi )$ whenever $\varphi$ and $\psi$ are in ${\mathcal {L}}_{PL}$. We again identify ${\mathcal {L}}$ with the set of its well-formed formulas.

(i) We resort to Popper functions for the probabilistic component of our acceptability conditions:

Definition 1

(Popper Functions) ${\mathcal {P}}:{\mathcal {L}}_{PL}\times {\mathcal {L}}_{PL}\rightarrow [0, 1]$ is a Popper function on ${\mathcal {L}}_{PL}\times {\mathcal {L}}_{PL}$ iff

• 1. for some $\alpha , \beta \in {\mathcal {L}}_{PL}$, ${\mathcal {P}}(\alpha | \beta )\ne 1$; and for all $\varphi , \psi , \chi , \eta \in {\mathcal {L}}_{PL}$,

• 2. if $\vDash _{PL} \psi \equiv \chi$, then ${\mathcal {P}}(\varphi | \psi )={\mathcal {P}}(\varphi | \chi )$,

• 3. if $\varphi \vDash _{PL} \psi$, then ${\mathcal {P}}(\psi | \varphi )=1$,

• 4. if $\varphi \vDash _{PL} \lnot (\psi \wedge \chi )$, then ${\mathcal {P}}(\psi \vee \chi |\varphi )={\mathcal {P}}(\psi |\varphi )+{\mathcal {P}}(\chi | \varphi )$ (i.e., ${\mathcal {P}}(\cdot |\varphi )$ is a finitely additive probability measure) or ${\mathcal {P}}(\eta | \varphi )=1$;

• 5. ${\mathcal {P}}(\psi \wedge \chi | \varphi )={\mathcal {P}}(\psi |\varphi ){\mathcal {P}}(\chi |\psi \wedge \varphi )$.

One could define Popper functions on ${\mathcal {L}}_{PL}$ without relying on the classical notion of logical truth/consequence (Hawthorne 1996, Definition 3). We work with the above definition, however, because it makes the connection between Popper functions and unconditional probability measures clear. The latter can be recovered from Popper functions by conditionalization on $\top$. If ${\mathcal {P}}(\varphi | \top )>0$, we have

$$\begin{aligned} \frac{{\mathcal {P}}(\varphi \wedge \psi | \top )}{{\mathcal {P}}(\varphi | \top )}={\mathcal {P}}(\psi | \varphi \wedge \top ) = {\mathcal {P}}(\psi |\varphi ). \end{aligned}$$

Popper functions allow for non-trivial conditionalization on 0 probabilities: we can have that ${\mathcal {P}}(\varphi |\top )=0$ but ${\mathcal {P}}(\psi |\varphi )\in (0, 1)$. We call an element $\varphi$ of ${\mathcal {L}}_{PL}$ abnormal with respect to ${\mathcal {P}}$ when ${\mathcal {P}}(\eta | \varphi )=1$ for all $\eta \in {\mathcal {L}}_{PL}$; normal otherwise.

(ii) The second component of our acceptability conditions needs a topicality filter:

Definition 2

(Topic models with operators) A topic model with operators (in short, topic model) $\mathcal {T}$ is a tuple $\langle T, \oplus , t, f \rangle$ where

• 1. T is a non-empty set of possible topics. We use variables $a, b, c \ (a_1, a_2, \dots )$ ranging over possible topics.

• 2. $\oplus : T \times T \rightarrow T$ is a binary idempotent, commutative, associative operation: topic fusion. We assume unrestricted fusion, that is, $\oplus$ is always defined on T: $\forall a, b\in T \ \exists c\in T (c=a\oplus b).$ We define topic parthood, denoted by $\sqsubseteq$, in a standard way as

  $$\forall a, b (a \sqsubseteq b \text{ iff } a \oplus b = b).$$

  Easily, $\sqsubseteq$ is a partial order on T.

• 3. $t: {\mathsf {Prop}}\rightarrow T$ is a topic function assigning a topic to each element in ${\mathsf {Prop}}$. t extends to the whole ${\mathcal {L}}_{PL}$ by taking the topic of a sentence $\varphi$ as the fusion of the elements in ${\mathsf {P}}_\varphi$:

  $$\begin{aligned} t(\varphi )=\oplus {\mathsf {P}}_\varphi = t(p_1)\oplus \dots \oplus t(p_k) \end{aligned}$$

  where ${\mathsf {P}}_\varphi =\{p_1, \dots , p_k\}.$ We abbreviate $t(\varphi )$ as $t_\varphi$.

• 4. $f: T \rightarrow T$ is a function on T that satisfies for all $a, b\in T$:

  • (a) $a \sqsubseteq f(a)$ (Inclusion);

  • (b) $f(a)=f(f(a))$ (Idempotence);

  • (c) $f(a \oplus b)=f(a)\oplus f(b)$ (Additivity);

T provides the topics sentences of our language can be about. Fusion $\oplus$ gives our little mereology of topics, as per Constraint (2) from our topicology above: $a \oplus b$ is the merging of topics a and b (‘Obama is tall and handsome’ and ‘Obama is tall or handsome’ are about Obama’s height and looks, the merging of the topics of ‘Obama is tall’ and of ‘Obama is handsome’); and it makes sense to say that topic a is part of topic b, $a \sqsubseteq b$ (Obama’s height is included in Obama’s height and looks as a part). Topic function t assigns topics recursively, in such a way as to guarantee that the logical connectives in ${\mathcal {L}}_{PL}$ be topic-transparent, as per Constraint (3) of our topicology above: $t_{\lnot \varphi } = t_\varphi$ and $t_{\varphi \wedge \psi } = t_\varphi \oplus t_\psi$.

Finally, f is a Kuratowski closure operator on the poset $(T, \sqsubseteq )$, mapping the topic of a sentence $\varphi$ to the topic of the relevant background assumptions $BA_\varphi$ determined by $\varphi$ and context.

Given this role of f, (4a–4c), the so-called Kuratowski axioms are well-motivated: Inclusion (4a) guarantees that the topic of the relevant background assumptions $BA_\varphi$ possibly expands, but always includes, the topic of the antecedent $\varphi$ that triggers the conditional supposition. This constraint fits with our assumption that $\varphi \in BA_\varphi$ and allows us to account for cases such as (11)–(13). Idempotence (4b) states that the set of background assumptions $BA_\varphi$ determined by $\varphi$ is complete: contemplating on the background assumptions triggered by $\varphi$ does not lead to new background assumptions unless given additional inputs. Finally, Additivity (4c) ensures that the topic of the relevant background assumptions $BA_\varphi$ determined by $\varphi$ is the same as the fusion of the topics of the relevant background assumptions determined by its more primitive components.²²

Given a topic model ${\mathcal {T}}=\langle T, \oplus , t, f \rangle$, we call a conditional of the form $\varphi \rightarrow \psi$ an on-topic conditional with respect to ${\mathcal {T}}$ iff $t_\psi \sqsubseteq f(t_\varphi )$. We call $\varphi \rightarrow \psi$ an on-topic conditional (simpliciter) if it is an on-topic conditional with respect to every topic model. Being on-topic is what makes a conditional relevant: the topic of its consequent is included in that contextually determined by its antecedent, and given via f.

Lemma 1

For any topic model ${\mathcal {T}}=\langle T, \oplus , t, f \rangle$ and $a, b\in T$, if $a\sqsubseteq b$ then $f(a)\sqsubseteq f(b)$.

Proof

Let ${\mathcal {T}}=\langle T, \oplus , t, f \rangle$ be a topic model and $a, b\in T$ such that $a\sqsubseteq b$, i.e., $a\oplus b=b$. Then, since f is well-defined, we have $f(a\oplus b)=f(b)$. Therefore, Definition 2.4c guarantees that $f(a)\oplus f(b)=f(b)$, i.e., $f(a)\sqsubseteq f(b)$. $\square$

We can now define the graded (un)acceptability conditions for the formulas of ${\mathcal {L}}$, and in particular for our indicatives:

Definition 3

(Degrees of (Un)Acceptability) For any Popper function ${\mathcal {P}}$ and topic model ${\mathcal {T}}$ defined on ${\mathcal {L}}_{PL}$, the degree of acceptability ${\mathcal {A}}_{{\mathcal {P}}, {\mathcal {T}}}: {\mathcal {L}}\rightarrow [0, 1]$ of an element in ${\mathcal {L}}$ is defined as:

• 1. for all $\varphi \in {\mathcal {L}}_{PL}$, ${\mathcal {A}}_{{\mathcal {P}}, {\mathcal {T}}}(\varphi )={\mathcal {P}}(\varphi | \top )$; and

• 2. ${\mathcal {A}}_{{\mathcal {P}}, {\mathcal {T}}}(\varphi \rightarrow \psi )={\left\{ \begin{array}{ll} {\mathcal {P}}(\psi | \varphi ), &{} \text{ if } t_\psi \sqsubseteq f(t_\varphi ) \\ 0 &{} \text{ otherwise }. \end{array}\right. }$

For any $\varphi \in {\mathcal {L}}$, the degree of unacceptability ${\mathcal {U}}_{{\mathcal {P}}, {\mathcal {T}}}(\varphi )$ is then given by ${\mathcal {U}}_{{\mathcal {P}}, {\mathcal {T}}}(\varphi )= 1- {\mathcal {A}}_{{\mathcal {P}}, {\mathcal {T}}}(\varphi ).$²³

When it is clear which Popper function and topic model are used, we omit the subscripts and simply write ${\mathcal {A}}$ and ${\mathcal {U}}$.

Definition 3 includes our main claim: the degree of acceptability of $\varphi \rightarrow \psi$ is (i) the probability of $\psi$ conditional on $\varphi$, as per AT, as long as (ii) $\varphi \rightarrow \psi$ is an on-topic indicative; otherwise $\varphi \rightarrow \psi$ is plainly unacceptable.

The degree of acceptability of a Boolean sentence $\psi \in {\mathcal {L}}_{PL}$ goes by ${\mathcal {P}}(\psi | \top )$, that is, ${\mathcal {A}}(\psi )={\mathcal {P}}(\psi | \top )$. Topic models play no role in stating the degree of acceptability of a Boolean sentence.

5 The logic of on-topic indicatives

‘Any complete theory of conditionals requires a theory of conditional inference’ (Evans and Over 2004, p. 168). Thus, we now investigate the logic of our on-topic indicatives. We present the closure principles of interest as premise-conclusion rules of the form ‘$\Gamma \vdash \Delta$’ where $\Gamma , \Delta \subseteq {\mathcal {L}}$ with $\Gamma =\emptyset$ for zero-premise rules. For any $\varphi \in {\mathcal {L}}_{PL}$, ‘$\vdash _{PL}\varphi$’ says that $\varphi$ is theorem of classical propositional logic. Following Adams (1998), we define validity probabilistically in terms of degrees of unacceptability:²⁴

Definition 4

(Validity) A principle of the form $\Gamma \vdash \Delta$ is valid if and only if for any Popper function ${\mathcal {P}}$ and topic model ${\mathcal {T}}$,

$$\sum \limits _{\varphi \in \Gamma } {\mathcal {U}}(\varphi )\ge {\mathcal {U}}(\psi ),$$

for all $\psi \in \Delta$. When $\Gamma =\emptyset$, we say $\vdash \Delta$ is valid if and only if ${\mathcal {U}}(\psi )=0$ for all $\psi \in \Delta$. $\Gamma \vdash \Delta$ is invalid otherwise.

Our notion of validity depends on two relatively independent constraints: (i) probability and (ii) relevance or topicality, as per our two-component account of acceptability. Besides investigating valid closure principles, we want to check that the invalid ones fail for the right reason. So we consider probabilistic validity and topical validity separately, and highlight the distinct sources of invalidity. However, our focus keeps being the notion of validity given in Definition 4. We use the notions of probabilistic and topical validity in order to point out the subtle reasons for invalidity.

We say that $\Gamma \vdash \Delta$ is probabilistically valid (p-valid) iff for any Popper function ${\mathcal {P}}$ and singleton topic model ${\mathcal {T}}$, $\sum \nolimits _{\varphi \in \Gamma } {\mathcal {U}}(\varphi )\ge {\mathcal {U}}(\psi ),$ for all $\psi \in \Delta$. When $\Gamma =\emptyset$, we say $\vdash \Delta$ is p-valid if and only if ${\mathcal {U}}(\psi )=0$ for all $\psi \in \Delta$; and $\Gamma \vdash \Delta$ is p-invalid otherwise.

We say $\Gamma \vdash \Delta$ is topically valid (t-valid) iff for any topic model ${\mathcal {T}}=\langle T, \oplus , t, f \rangle$, if every conditional in $\Gamma$ is an on-topic conditional wrt ${\mathcal {T}}$ then every conditional in $\Delta$ is also an on-topic conditional wrt ${\mathcal {T}}$; and $\Gamma \vdash \Delta$ is t-invalid otherwise.

Our p-validity works similarly to Adams’ p-validity—except that we define it in terms of Popper functions instead of unconditional probability functions—and it bypasses the topicality constraint. t-validity ignores probabilistic constraints and checks whether a closure principle satisfies the required relevance condition. The following lemma relates validity simpliciter to p- and t-validity and vice versa:

Lemma 2

If $\Gamma \vdash \Delta$ is valid then it is p-valid but not necessarily t-valid. If $\Gamma \vdash \Delta$ is both p- and t-valid, then it is valid.

Proof

For the first part, it is easy to see that validity implies p-validity by definition: the latter is a special case of the former obtained by restricting validity to the class of singleton topic models. As an example of an inference which is valid but t-invalid, consider $p\wedge \lnot p \vdash p\rightarrow q$. To show its validity, let ${\mathcal {P}}$ be a Popper function and ${\mathcal {T}}$ be a topic model on ${\mathcal {L}}_{PL}$. By Definitions 1 and 3, we have ${\mathcal {A}}(p\wedge \lnot p)={\mathcal {P}}(p\wedge \lnot p |\top )=0$, thus, ${\mathcal {U}}(p\wedge \lnot p)=1$. As ${\mathcal {U}}(p\rightarrow q)\in [0, 1]$ by the definition of ${\mathcal {U}}$, we obtain that ${\mathcal {U}}(p\wedge \lnot p)\ge {\mathcal {U}}(p\rightarrow q)$. To show its t-invalidity, consider the topic model $\langle \{a, b\}, \oplus , f, t\rangle$ such that $\oplus$ is idempotent and $a\oplus b=a$, thus, $b\sqsubset a$. Moreover, f is a constant function and $t_p=b$ and $t_q=a$. Therefore, $b=t_p=f(t_{p})$ but $a=t_q\not \sqsubseteq f(t_p)=b$ (see Fig. 1).

For the second part, suppose that $\Gamma \vdash \Delta$ is both p- and t-valid. Let ${\mathcal {P}}$ a Popper function and ${\mathcal {T}}$ a topic model. Since $\Gamma \vdash \Delta$ is t-valid, we have two cases:

Case 1: Every conditional in $\Gamma \cup \Delta$ is an on-topic conditional wrt ${\mathcal {T}}$.

Then, it is easy to see that validity and p-validity coincide, thus, $\Gamma \vdash \Delta$ is valid.

Case 2: There is a conditional in $\Gamma$ that is not an on-topic conditional wrt ${\mathcal {T}}$.

Wlog, suppose that $\varphi \in \Gamma$ is not an on-topic conditional wrt ${\mathcal {T}}$. This means that ${\mathcal {U}}_{{\mathcal {P}}, {\mathcal {T}}}(\varphi )=1$ (by the definition of ${\mathcal {U}}_{{\mathcal {P}}, {\mathcal {T}}}$). Recall that ${\mathcal {U}}_{{\mathcal {P}}, {\mathcal {T}}}(\chi )\in [0, 1]$ for all $\chi \in {\mathcal {L}}$. Therefore, we conclude that $\sum \nolimits _{\varphi \in \Gamma } {\mathcal {U}}_{{\mathcal {P}}, {\mathcal {T}}}(\varphi )\ge {\mathcal {U}}_{{\mathcal {P}}, {\mathcal {T}}}(\chi )$ for all $\chi \in \Delta$. $\square$

Fig. 1

Topic model $\langle \{a, b\}, \oplus , t, f\rangle$

We now focus on the closure principles given in Table 1 (we label them, again, following Douven (2016), who sticks to popular names from the literature). The following is our main technical result:

Table 1 Closure principles of interest

Theorem 3

• 1. REF, ANT, CM, CC, CSO, CT, CMon, OR, and Modus Ponens are both p- and t-valid. Therefore, they all are valid.

• 2. MOD, RCE, RCEA, RCEC, RCK, RCM, and And-to-If are p-valid but t-invalid.

• 3. Trans and SA are p-invalid but t-valid.

• 4. Or-to-if, Contraposition, and SDA are both p-invalid and t-invalid.

• 5. MOD, RCE, RCEA, RCEC, RCK, RCM, And-to-If, Trans, SA, Or-to-If, Contraposition, and SDA are invalid.

Proof

See “Appendix”. $\square$

Table 2 Validities ($\checkmark$) and invalidities ($X$): summary of the results in Theorem 3

We comment on some notable validities and invalidities. As for the former, REF (Reflexivity) and ANT appear fairly obvious. CC, CT and CMon have already been discussed above.²⁵ Modus Ponens, we have argued, is desirable. The other validities hold in most conditional logics and theories of non-monotonic entailment (see Nute 1984, for a classic survey).

The invalidities in group 2 are all related to the hyperintensional acceptability conditions of conditionals: they are p-valid, but fail to be valid due to topicality. Look for instance at RCEA and RCEC: that $\varphi$ and $\psi$ are classically-necessarily equivalent doesn’t guarantee their replacement in the antecedent or consequent of a conditional to preserve acceptability. Taking ‘5 is prime’ and ‘One cannot square the circle’ as necessarily equivalent (qua true in all possible worlds), our sample conditionals above, (9) (‘If all even numbers are prime and 5 is even, then 5 is prime’) and (10) (‘If all even numbers are prime and 5 is even, then one cannot square the circle’) are not both acceptable: only the former’s consequent is on-topic with respect to the antecedent. Or, look at RCE: that $\varphi$ classically entails $\psi$ doesn’t make the corresponding conditional acceptable. ‘Obama is tall’ entails ‘Either it is raining in Melbourne or not’ in classical logic, but we don’t assert ‘If Obama is tall, then either it is raining in Melbourne or not’, as the latter is patently off-topic.

One validity in group 1, namely CSO, stands out for comparison with such invalidities, for it limits the hyperintensional anarchy of indicatives. Even if replacement of necessary equivalents fails to preserve acceptability, CSO guarantees that replacement of conditional equivalents does: when both $\varphi \rightarrow \psi$ and the converse $\psi \rightarrow \varphi$ are among the premises ($\varphi$ and $\psi$ are taken as ‘conditional equivalents’ in this sense), the inference from these and $\varphi \rightarrow \chi$ to the conditional obtained by replacing $\varphi$ with $\psi$ in the latter, namely $\psi \rightarrow \chi$, is valid.

Groups 3 and 4 include inferences generally agreed to be invalid for any ceteris paribus conditional in the indicative and even in the subjunctive-counterfactual mood: SA (Strengthening the Antecedent), Contraposition, Transitivity, SDA (Simplification of Disjunctive Antecedents), Or-to-If, fail both in the Adams (1998) probabilistic semantics for indicatives and in the possible worlds semantics for indicatives and/or counterfactuals by Stalnaker (1968) and Lewis (1973).

Finally, And-to-If fails in the most natural way: the inference from $\varphi \wedge \psi$ to $\varphi \rightarrow \psi$ fails to be acceptability-preserving due to the topicality constraint: the latter may be an off-topic conditional like our (5) above (‘If raccoons have no wings, then they cannot breath under water’) although the former is a true and acceptable conjunction like our (4) (‘Raccoons have no wings and they cannot breath under water’). Although the conjuncts plausibly overlap in topic (they are both about raccoons), which makes the conjunction coherently assertable in discourse, the topic of ‘Raccoons cannot breath under water’ is not fully included in that of the background assumptions contextually triggered by ‘Raccoons have no wings’.

Such (in)validities make for a conditional logic that is not only theoretically desirable, but also empirically plausible. As noted e.g. in (Evans and Over 2004, pp. 44–5), the vast majority of experimental results concerning how people reason with conditionals only involve four simple inferences: Modus Ponens, Modus Tollens, and the usual fallacies of Affirming the Consequent and Denying the Antecedent. There are few studies investigating other conditional inferences (we mentioned (Pfeifer and Kleiter 2010) above as one notable exception). However, an initial and tentative assessment of the psychological plausibility of our logic is possible, thanks to a sophisticated experiment reported in (Douven 2016, Ch. 5).

Acknowledging that many inferences considered in the literature on conditional logics, including various among those in our table, are of a kind that people would rarely make in everyday reasoning, Douven went on to test them experimentally in a more roundabout way. Here’s a summary of what he did (the detailed presentation is in pp. 140ff of Douven’s book).

Most inferences involving simple conditionals in conditional logic feature at most three propositions (expressed by sentences) $\varphi , \psi$, and $\chi$. So Douven asked over 1,000 subjects to rate the probabilities of conjunctions of the form $\pm \varphi \wedge \pm \psi \wedge \pm \chi$ (called atoms), with ‘$\pm\$$’ indicating that sentence $\$$ may occur negated or unnegated, and $\varphi , \psi , \chi$ taken from news websites. For each triple of sentences, there are eight mutually exclusive and jointly exhaustive combinations (exactly one of them has to be true), composing an atom matrix. Subjects were instructed that the truth of any element of the matrix would exclude that of all the others, and that one of the elements had to be true, so that the probabilities assigned to the atoms had to add up to 100%. Douven then computed which conditional-involving inferences with $\varphi , \psi , \chi$ end up acceptability-preserving. He checked acceptability-preservation for two thresholds, $\theta = 0.5$ and $\theta = 0.9$. The results summarized in the table of (Douven 2016, p. 144) show that the validities of our logic tested in the experiment correspond to highly popular inferences: CC has percentages of 100/100 endorsement (for 0.5 and 0.9 respectively); CSO has 75/100; CT has 87/94; CMon has 86/100; Modus Ponens has 91/78. Vice versa, some invalidities have low endorsement rates: Or-to-If has 28/9; SDA has 44/56.

An open problem is that the three inferences of Contraposition (70/78), SA (76/97) and Transitivity (78/100) are highly endorsed. However, these are invalid, as we mentioned, in any conditional logic for non-monotonic and ceteris paribus conditionals. Their invalidity, furthermore, is not due specifically to the distinctive element of our semantics for the indicative, namely our topicality constraint: they are invalidated purely probabilistically in semantics à la Adams, and they fail also in similarity-based possible worlds semantics à la Stalnaker-Lewis, due to conditionals being ‘variably strict’ (Lewis 1973, p. 13) in this approach. Unsurprisingly, therefore, authors endorsing some variant of any of these treatments of conditionals have come up with explanations for the popularity of such invalid inferences. In particular, the fact that the three of them are more popular with higher 0.9 threshold than with lower 0.5, may corroborate the story proposed in Adams (1998), Bennett (2003): such inferences fail for non-perfectly-certain propositions, so it is plausible that their endorsement grows as we lift the threshold towards certainty, i.e., probability 1. They tend to be endorsed to the extent that they are mistaken for their limited counterparts, like Cautious Monotonicity (CMon) and Cautious Transitivity (CT).

We have focused on closure principles that are more commonly discussed in the context of conditional logics and non-monotonic reasoning, and empirically tested by Douven (2016). A more exhaustive list can be found, e.g., in (Douven 2016, p. 129) and (Crupi and Iacona 2019, p. 6). How to extend our analysis for those additional principles should be obvious. We can adopt the components of Crupi and Iacona (2019)’s framework concerning the operators necessity ($\Box$), possibility ($\Diamond$), and negation ($\sim$), and evaluate the principles involving them with respect to our topic-sensitive semantics.

6 Conclusion

We have presented a general semantics giving acceptability conditions for simple indicatives. The semantics preserves good features of probabilistic approaches to conditionals while fixing their troubles with relevance: we accept a conditional to the extent that its consequent is likely conditional on the antecedent, provided there’s a relevant connection between antecedent and consequent. We have proposed that relevance be understood as topic-sensitivity, adopting a theory of topics that captures common features of various recently burgeoning subject matter semantics.

We have, then, presented the logic of on-topic conditionals; and we have argued that the closure principles (in)validated by the logic are both theoretically plausible, and in line with empirical results on how people reason with conditionals. In particular, our logic of on-topic indicatives fares better than EST with Douven (2016)’s experimental results as it validates the highly endorsed principles—CC, CSO, CT, CMon, and Modus Ponens—that fail with respect to EST. Our proposal also does a better job than AT in tracking relevance between the antecedent and consequent of an indicative conditional. Invalidities MOD, RCE, RCEA, RCEC, RCK, RCM, and And-to-If are all related to the hyperintensional acceptability conditions of conditionals: they are valid in Adams (1998)’s probabilistic semantics for indicatives, but fail to be valid in our account due to our topicality constraint.

We haven’t conducted new experiments on reasoning with conditionals, but presented a logic that aligns nicely with the existing experimental results. However, we mention the following as a possible direction of further work (thanks to an anonymous referee): one could operationalize the notion of topicality for conditionals, and then carry out experiments specifically designed to test the original component of our logic, topicality, separately from its probabilistic component.

Appendix: Proof of Theorem 3

The following lemma is well known and will be useful in proving Theorem 3.

Lemma 4

For any Popper function ${\mathcal {P}}:{\mathcal {L}}_{PL}\times {\mathcal {L}}_{PL}\rightarrow [0, 1]$ and $\varphi , \psi , \chi \in {\mathcal {L}}_{PL}$, we have

• 1. if $\varphi$ is normal, then ${\mathcal {P}}(\lnot \psi | \varphi )=1- {\mathcal {P}}(\psi | \varphi )$;

• 2. $\vDash _{PL} \varphi \equiv \psi$, then ${\mathcal {P}}(\varphi | \chi )={\mathcal {P}}(\psi | \chi )$;

• 3. if $\varphi \vDash _{PL} \psi$, ${\mathcal {P}}(\psi | \chi )\ge {\mathcal {P}}(\varphi | \chi )$; and

• 4. ${\mathcal {P}}(\varphi \wedge \psi |\chi )={\mathcal {P}}(\varphi |\chi )+{\mathcal {P}}(\psi |\chi )-{\mathcal {P}}(\varphi \vee \psi |\chi )$.

Proof

Let ${\mathcal {P}}$ be a Popper function and $\varphi , \psi , \chi \in {\mathcal {L}}_{PL}$.

• 1. Suppose that $\varphi$ is normal. We know that $\varphi \vDash _{PL} \psi \vee \lnot \psi$ for all $\psi \in {\mathcal {L}}_{PL}$. Then, by Definition 1.3, ${\mathcal {P}}(\psi \vee \lnot \psi | \varphi )=1$. Moreover, $\psi$ and $\lnot \psi$ are obviously logically inconsistent. Then, by Definition 1.4, we have that ${\mathcal {P}}(\lnot \psi | \varphi )=1- {\mathcal {P}}(\psi | \varphi )$.

• 2. We have two cases:

  Case 1: $\chi$ is abnormal

  Then, the result follows by the definition of abnormal sentences. In particular we have ${\mathcal {P}}(\varphi | \chi )={\mathcal {P}}(\psi | \chi )=1$.

  Case 2: $\chi$ is normal

  Suppose $\vDash _{PL} \varphi \equiv \psi$. Then, $\chi \vDash _{PL} \lnot \varphi \vee \psi$ and $\chi \vDash _{PL}\varphi \vee \lnot \psi$. Thus, by Definition 1.3, we have that ${\mathcal {P}}(\lnot \varphi \vee \psi | \chi )=1$ and ${\mathcal {P}}(\varphi \vee \lnot \psi | \chi )=1$. Moreover, we know that $\vDash _{PL}\lnot (\lnot \varphi \wedge \psi )$ and $\vDash _{PL} \lnot (\varphi \wedge \lnot \psi )$. Thus, by Definition 1.4, we obtain that

  $$\begin{aligned}&{\mathcal {P}}(\lnot \varphi \vee \psi | \chi ) ={\mathcal {P}}(\lnot \varphi | \chi ) + {\mathcal {P}}(\psi |\chi ) \ \text{ and } \\&{\mathcal {P}}(\varphi \vee \lnot \psi | \chi ) ={\mathcal {P}}(\varphi | \chi ) + {\mathcal {P}}(\lnot \psi |\chi ). \end{aligned}$$

  As ${\mathcal {P}}(\lnot \varphi \vee \psi | \chi )= {\mathcal {P}}(\varphi \vee \lnot \psi | \chi )=1$, we conclude that ${\mathcal {P}}(\varphi |\chi )={\mathcal {P}}(\psi |\chi )$.

• 3. We have two cases:

  Case 1: $\chi$ is abnormal

  Follows by the definition of abnormal sentences.

  Case 2: $\chi$ is normal

  Suppose that $\varphi \vDash _{PL} \psi$. By classical propositional logic, we have that $\vDash _{PL}\lnot ((\lnot \varphi \wedge \psi )\wedge \varphi )$. Then, by Definition 1.4, we obtain that ${\mathcal {P}}((\lnot \varphi \wedge \psi )\vee \varphi | \chi )={\mathcal {P}}(\lnot \varphi \wedge \psi | \chi ) + {\mathcal {P}}(\varphi | \chi )$. As $\varphi \vDash _{PL} \psi$, we have that $\vDash _{PL} ((\lnot \varphi \wedge \psi )\vee \varphi )\equiv \psi$, thus, by Lemma 4.2, we obtain ${\mathcal {P}}((\lnot \varphi \wedge \psi )\vee \varphi | \chi )={\mathcal {P}}(\psi |\chi )$, i.e., ${\mathcal {P}}(\lnot \varphi \wedge \psi | \chi ) + {\mathcal {P}}(\varphi | \chi )={\mathcal {P}}(\psi |\chi )$. Then, since ${\mathcal {P}}(\lnot \varphi \wedge \psi | \chi )\in [0, 1]$, we obtain that ${\mathcal {P}}(\psi | \chi )\ge {\mathcal {P}}(\varphi | \chi )$.

• 4. We have two cases:

  Case 1: $\chi$ is abnormal

  Then, the result follows by the definition of abnormal sentences.

  Case 2: $\chi$ is normal

  By Definition 1.4 and Lemma 4.2, we have

  • (a) ${\mathcal {P}}(\varphi | \chi ) = {\mathcal {P}}(\varphi \wedge \psi | \chi ) +{\mathcal {P}}(\varphi \wedge \lnot \psi | \chi )$, and

  • (b) ${\mathcal {P}}(\psi | \chi ) = {\mathcal {P}}(\varphi \wedge \psi | \chi ) +{\mathcal {P}}(\lnot \varphi \wedge \psi | \chi )$.

  Thus,

  $$\begin{aligned} {\mathcal {P}}(\varphi | \chi ) + {\mathcal {P}}(\psi | \chi )&= {\mathcal {P}}(\varphi \wedge \psi | \chi )+( {\mathcal {P}}(\varphi \wedge \psi | \chi ) +{\mathcal {P}}(\varphi \wedge \lnot \psi | \chi )+{\mathcal {P}}(\lnot \varphi \wedge \psi | \chi ))\\&= {\mathcal {P}}(\varphi \wedge \psi | \chi ) + {\mathcal {P}}(\varphi \vee \psi | \chi ) \qquad (\text {Defn.}\,1.4\ \text {and Lemma}\,4.\text {2}) \end{aligned}$$

  I.e., ${\mathcal {P}}(\varphi \wedge \psi |\chi ) ={\mathcal {P}}(\varphi |\chi )+{\mathcal {P}}(\psi |\chi )-{\mathcal {P}}(\varphi \vee \psi |\chi )$.

$\square$

1.1 Proof of Theorem 3.1

Let ${\mathcal {P}}$ be a Popper function and ${\mathcal {T}}=\langle T, \oplus , t, f \rangle$ be a topic model. We first show that REF, ANT, CM, CC, CSO, CT, CMon, OR, and Modus Ponens are both p- and t-valid. Therefore, by Lemma 2, they are also valid.

Given a premise-conclusion rule $\Gamma \vdash \Delta$, we only consider the cases where the antecedents of the conditionals in $\Delta$ are normal with respect to the given Popper function since otherwise the degrees of unacceptability of the conclusions equal to 0. And, due to the structure of the rules in Theorem 3.1, we cannot have that the antecedents of all the premises are abnormal but the antecedent of the conclusion is not.

REF: $\vdash \varphi \rightarrow \varphi$

t-valid: By Definition 2.4a, we have that $t_\varphi \sqsubseteq f(t_\varphi )$.

p-valid: By Definition 1.3, we have ${\mathcal {P}}(\varphi |\varphi )=1$. Moreover, we also have that $t_\varphi \sqsubseteq f(t_\varphi )$. Therefore, ${\mathcal {U}}(\varphi \rightarrow \varphi )=1-{\mathcal {P}}(\varphi |\varphi )=0$.

ANT: $\varphi \rightarrow \psi \vdash \varphi \rightarrow (\varphi \wedge \psi )$

t-valid: Suppose that $t_\psi \sqsubseteq f(t_\varphi )$. Then, since $t_\varphi \sqsubseteq f(t_\varphi )$ (Definition 2.4a), we obtain that $t_{\varphi \wedge \psi } =t_\varphi \oplus t_\psi \sqsubseteq f(t_\varphi )$.

p-valid: Now suppose that T is a singleton. Therefore, ${\mathcal {U}}(\varphi \rightarrow \psi )=1- {\mathcal {P}}(\psi |\varphi )$ and ${\mathcal {U}}(\varphi \rightarrow (\varphi \wedge \psi ))=1-{\mathcal {P}}(\varphi \wedge \psi | \varphi )$. Observe that ${\mathcal {P}}(\varphi \wedge \psi | \varphi )={\mathcal {P}}(\varphi | \varphi ) + {\mathcal {P}}( \psi | \varphi )-{\mathcal {P}}(\varphi \vee \psi | \varphi )$ (by Lemma 4.4), where ${\mathcal {P}}(\varphi | \varphi ) =1$ and ${\mathcal {P}}(\varphi \vee \psi | \varphi )=1$ (by Definition 1.3). Therefore, ${\mathcal {U}}(\varphi \rightarrow \psi )={\mathcal {U}}(\varphi \rightarrow (\varphi \wedge \psi ))$.

CM: $\varphi \rightarrow (\psi \wedge \chi )\vdash \varphi \rightarrow \psi , \varphi \rightarrow \chi$

t-valid: Suppose that $t_{\psi \wedge \chi } \sqsubseteq f(t_\varphi )$. Then, since $t_{\psi }, t_\chi \sqsubseteq t_\psi \oplus t_\chi =t_{\psi \wedge \chi } \sqsubseteq f(t_\varphi )$ and $\sqsubseteq$ is transitive, we conclude that $t_{\psi }, t_\chi \sqsubseteq f(t_\varphi )$.

p-valid: Now suppose that T is a singleton. Therefore, ${\mathcal {U}}(\varphi \rightarrow (\psi \wedge \chi ))=1-{\mathcal {P}}(\psi \wedge \chi | \varphi )$, ${\mathcal {U}}(\varphi \rightarrow \psi )=1-{\mathcal {P}}(\psi |\varphi )$, and ${\mathcal {U}}(\varphi \rightarrow \chi )=1-{\mathcal {P}}(\chi |\varphi )$. Since $\psi \wedge \chi \vDash _{PL} \psi$ and $\psi \wedge \chi \vDash _{PL} \chi$, by Lemma 4.3, we know that ${\mathcal {P}}(\psi \wedge \chi | \varphi )\le {\mathcal {P}}(\psi | \varphi )$ and ${\mathcal {P}}(\psi \wedge \chi | \varphi )\le {\mathcal {P}}(\chi | \varphi )$. Therefore, ${\mathcal {U}}(\varphi \rightarrow (\psi \wedge \chi ))\ge {\mathcal {U}}(\varphi \rightarrow \psi )$ and ${\mathcal {U}}(\varphi \rightarrow (\psi \wedge \chi ))\ge {\mathcal {U}}(\varphi \rightarrow \chi )$.

CC: $\varphi \rightarrow \psi , \varphi \rightarrow \chi \vdash \varphi \rightarrow (\psi \wedge \chi )$

t-valid: Suppose that $t_\psi \sqsubseteq f(t_\varphi )$ and $t_\chi \sqsubseteq f(t_\varphi )$. Then, by the properties of $\oplus$, we obtain that $t_{\psi \wedge \chi }\sqsubseteq t_\psi \oplus t_\chi \sqsubseteq f(t_\varphi )$.

p-valid: Now suppose that T is a singleton. We then have

$$\begin{aligned} {\mathcal {U}}(\varphi \rightarrow \psi ) + {\mathcal {U}}(\varphi \rightarrow \chi )&= 1-{\mathcal {P}}(\psi |\varphi ) + 1-{\mathcal {P}}(\chi |\varphi )\\&\ge 1- {\mathcal {P}}(\psi |\varphi ) -{\mathcal {P}}(\chi |\varphi ) + {\mathcal {P}}(\psi \vee \chi | \varphi )\qquad ({\mathcal {P}}(\psi \vee \chi | \varphi ) \le 1) \\&= 1 - {\mathcal {P}}(\psi \wedge \chi | \varphi )\qquad (\text {Lemma}\,4.\text {4})\\&= {\mathcal {U}}(\varphi \rightarrow (\psi \wedge \chi )) \qquad (\text {by the defn. of}\ {\mathcal {U}}) \end{aligned}$$

CSO: $\varphi \rightarrow \psi , \psi \rightarrow \varphi , \varphi \rightarrow \chi \vdash \psi \rightarrow \chi$

t-valid: Suppose that $t_\varphi \sqsubseteq f(t_\psi )$, $t_\psi \sqsubseteq f(t_\varphi )$, and $t_\chi \sqsubseteq f(t_\varphi )$. Then, by the former two, Lemma 1, and Definition 2.4b, we have $f(t_\psi )=f(t_\varphi )$. Therefore, we obtain that $t_\chi \sqsubseteq f(t_\psi )$.

p-valid: Now suppose that T is a singleton. Then, ${\mathcal {U}}(\varphi \rightarrow \psi )=1-{\mathcal {P}}(\psi | \varphi )$, ${\mathcal {U}}( \psi \rightarrow \varphi )= 1-{\mathcal {P}}(\varphi | \psi )$, ${\mathcal {U}}( \varphi \rightarrow \chi ) =1-{\mathcal {P}}(\chi | \varphi )$, and ${\mathcal {U}}( \psi \rightarrow \chi )=1-{\mathcal {P}}(\chi | \psi )$. To simplify notation, we represent the conditional probabilities on $\psi \vee \chi \vee \varphi$ by using the diagram in Figure 2 (similar to Adams (1998)’s diagrams). Each region of the diagram is identified with the set theoretic counterpart of Boolean combinations of $\psi$, $\chi$, and $\varphi$, and each letter represents the probability of its region conditional on $\psi \vee \chi \vee \varphi$. For example, ${\mathcal {P}}(\varphi \wedge \lnot \psi \wedge \lnot \chi | \psi \vee \chi \vee \varphi )=x$, ${\mathcal {P}}(\varphi \wedge \psi \wedge \lnot \chi | \psi \vee \chi \vee \varphi )=y$, and ${\mathcal {P}}(\varphi \wedge \psi \wedge \chi | \psi \vee \chi \vee \varphi )=k$ etc.

Fig. 2

Diagram for the Popper function ${\mathcal {P}}(\cdot | \psi \vee \chi \vee \varphi )$

By Definition 1.2, 1.4 and 1.5, observe that

• 1. ${\mathcal {P}}(\psi | \varphi )={\mathcal {P}}(\psi |\varphi \wedge (\psi \vee \chi \vee \varphi )) =\frac{{\mathcal {P}}(\psi \wedge \varphi |\psi \vee \chi \vee \varphi )}{{\mathcal {P}}(\varphi |\psi \vee \chi \vee \varphi )}=\frac{y+k}{x+y+w+k}$,

• 2. ${\mathcal {P}}(\varphi | \psi )={\mathcal {P}}(\varphi |\psi \wedge (\psi \vee \chi \vee \varphi )) =\frac{{\mathcal {P}}(\psi \wedge \varphi |\psi \vee \chi \vee \varphi )}{{\mathcal {P}}(\psi |\psi \vee \chi \vee \varphi )}=\frac{y+k}{y+z+k+t}$,

• 3. ${\mathcal {P}}(\chi | \varphi )={\mathcal {P}}(\chi |\varphi \wedge (\psi \vee \chi \vee \varphi )) =\frac{{\mathcal {P}}(\chi \wedge \varphi |\psi \vee \chi \vee \varphi )}{{\mathcal {P}}(\varphi |\psi \vee \chi \vee \varphi )}=\frac{w+k}{x+y+w+k}$, and

• 4. ${\mathcal {P}}(\chi | \psi )={\mathcal {P}}(\chi |\psi \wedge (\psi \vee \chi \vee \varphi )) =\frac{{\mathcal {P}}(\chi \wedge \psi |\psi \vee \chi \vee \varphi )}{{\mathcal {P}}(\psi |\psi \vee \chi \vee \varphi )}=\frac{t+k}{y+z+k+t}$.

Note also that $1={\mathcal {P}}(\psi \vee \chi \vee \varphi | \psi \vee \chi \vee \varphi )=x+y+z+w+k+t+r$. Thus, we need to show that

$$\begin{aligned} \frac{w+x}{x+y+w+k} + \frac{z+t}{y+z+k+t} + \frac{x+y}{x+y+w+k}\ge \frac{y+z}{y+z+k+t}. \end{aligned}$$

This can easily be established by tedious but simple algebra.

CT: $\varphi \rightarrow \psi , (\varphi \wedge \psi )\rightarrow \chi \vdash \varphi \rightarrow \chi$

t-valid: Suppose that $t_\psi \sqsubseteq f(t_\varphi )$ and $t_\chi \sqsubseteq f(t_{\varphi \wedge \psi })$. The former, by Lemma 1 and Definition 2.4b, implies that $f(t_\psi ) \sqsubseteq f(t_\varphi )$. Then, by Definition 2.4c, we obtain that $f(t_{\varphi \wedge \psi }) = f(t_\varphi \oplus t_\psi )=f(t_\varphi )\oplus f(t_\psi )=f(t_\varphi )$. Hence, since $t_\chi \sqsubseteq f(t_{\varphi \wedge \psi })$, we have $t_\chi \sqsubseteq f(t_\varphi )$.

p-valid: Now suppose that T is a singleton. Therefore, we have that ${\mathcal {U}}(\varphi \rightarrow \psi )=1-{\mathcal {P}}(\psi | \varphi )$, ${\mathcal {U}}((\varphi \wedge \psi )\rightarrow \chi )= 1-{\mathcal {P}}(\chi | \varphi \wedge \psi )$, and ${\mathcal {U}}(\varphi \rightarrow \chi )=1-{\mathcal {P}}(\chi | \varphi ).$ Observe that, by Definition 1.4 and Lemma 4.2, we have ${\mathcal {P}}(\psi | \varphi ) = {\mathcal {P}}(\psi \wedge \chi | \varphi )+ {\mathcal {P}}(\psi \wedge \lnot \chi | \varphi )$, ${\mathcal {P}}(\chi | \varphi ) = {\mathcal {P}}(\psi \wedge \chi | \varphi ) +{\mathcal {P}}(\lnot \psi \wedge \chi | \varphi )$, and by Definition 1.5, ${\mathcal {P}}(\chi |\psi \wedge \varphi )=\frac{{\mathcal {P}}(\psi \wedge \chi | \varphi )}{{\mathcal {P}}(\psi |\varphi )}$. To ease the notation, let ${\mathcal {P}}(\psi \wedge \chi | \varphi )=x$, ${\mathcal {P}}(\psi \wedge \lnot \chi | \varphi )=y$, ${\mathcal {P}}(\lnot \psi \wedge \chi | \varphi )=z$, and ${\mathcal {P}}(\lnot \psi \wedge \lnot \chi | \varphi )=w$. Obviously, $x+y+z+w = {\mathcal {P}}(\top |\varphi )$ (by Definition 1.4) = 1 (by Definition 1.3). Then, ${\mathcal {U}}(\varphi \rightarrow \psi ) = z+w$, ${\mathcal {U}}(\varphi \rightarrow \chi )=y+w$ and ${\mathcal {U}}( (\varphi \wedge \psi )\rightarrow \chi )=\frac{y}{x+y}$. Since $\frac{y}{x+y}\ge y$, we conclude that $z+w+\frac{y}{x+y} \ge y+w$, that is, ${\mathcal {U}}(\varphi \rightarrow \psi )+{\mathcal {U}}( (\varphi \wedge \psi )\rightarrow \chi )\ge {\mathcal {U}}(\varphi \rightarrow \chi )$.

CMon: $\varphi \rightarrow \psi , \varphi \rightarrow \chi \vdash (\varphi \wedge \psi )\rightarrow \chi$

t-valid: Suppose that $t_\psi \sqsubseteq f(t_\varphi )$ and $t_\chi \sqsubseteq f(t_\varphi )$. The latter, by Definition 2.4, implies that $t_\chi \sqsubseteq f(t_{\varphi \wedge \psi })$.

p-valid: Now suppose that T is a singleton. Then, ${\mathcal {U}}(\varphi \rightarrow \psi )=1-{\mathcal {P}}(\psi | \varphi )$, ${\mathcal {U}}( \varphi \rightarrow \chi )= 1-{\mathcal {P}}(\chi | \varphi )$, and ${\mathcal {U}}((\varphi \wedge \psi ) \rightarrow \chi )=1-{\mathcal {P}}(\chi | \varphi \wedge \psi ).$ Observe that

$$\begin{aligned} {\mathcal {P}}(\chi | \varphi \wedge \psi )&= \frac{{\mathcal {P}}(\psi \wedge \chi | \varphi )}{{\mathcal {P}}(\psi | \varphi )} \qquad (\text {Definition}\,1.\text {5})\\&\ge {\mathcal {P}}(\psi \wedge \chi | \varphi )\qquad (\text {since}\ {\mathcal {P}}(\psi | \varphi )\in [0, 1])\\&= {\mathcal {P}}(\psi | \varphi ) + {\mathcal {P}}( \chi | \varphi ) -{\mathcal {P}}(\psi \vee \chi | \varphi ) \qquad (\text {Lemma}\,4.\text {4})\\&\ge {\mathcal {P}}(\psi | \varphi ) + {\mathcal {P}}( \chi | \varphi ) -1 \qquad ({\mathcal {P}}(\psi \vee \chi | \varphi ) \le 1) \end{aligned}$$

Therefore, ${\mathcal {U}}(\varphi \rightarrow \psi )+{\mathcal {U}}(\varphi \rightarrow \chi ) = 2- {\mathcal {P}}(\psi | \varphi ) - {\mathcal {P}}( \chi | \varphi ) \ge 1- {\mathcal {P}}(\chi | \varphi \wedge \psi ) ={\mathcal {U}}((\varphi \wedge \psi ) \rightarrow \chi )$.

OR: $\varphi \rightarrow \psi , \chi \rightarrow \psi \vdash (\varphi \vee \chi )\rightarrow \psi$

t-valid: Suppose that $t_\psi \sqsubseteq f(t_\varphi )$ and $t_\psi \sqsubseteq f(t_\chi )$. The latter implies that $t_\psi \sqsubseteq f(t_{\varphi \vee \chi })$ (by Lemma 1 and the fact that $t_\chi \sqsubseteq t_{\varphi \vee \chi }$).

p-valid: Now suppose that T is a singleton. Then, ${\mathcal {U}}(\varphi \rightarrow \psi )=1-{\mathcal {P}}(\psi | \varphi )$, ${\mathcal {U}}( \chi \rightarrow \psi )= 1-{\mathcal {P}}(\psi | \chi )$, and ${\mathcal {U}}((\varphi \vee \chi ) \rightarrow \psi )=1-{\mathcal {P}}(\psi | \varphi \vee \chi ).$ By Definition 1.2, 1.4 and 1.5, observe that

• 1. ${\mathcal {P}}(\psi | \varphi )={\mathcal {P}}(\psi |\varphi \wedge (\varphi \vee \chi ))=\frac{{\mathcal {P}}(\varphi \wedge \psi |\varphi \vee \chi )}{{\mathcal {P}}(\varphi |\varphi \vee \chi )}=\frac{{\mathcal {P}}(\varphi \wedge \psi |\varphi \vee \chi )}{{\mathcal {P}}(\varphi \wedge \psi |\varphi \vee \chi ) +{\mathcal {P}}(\varphi \wedge \lnot \psi |\varphi \vee \chi )}$,

• 2. ${\mathcal {P}}(\psi | \chi )={\mathcal {P}}(\psi |\chi \wedge (\varphi \vee \chi ))=\frac{{\mathcal {P}}(\chi \wedge \psi |\varphi \vee \chi )}{{\mathcal {P}}(\chi |\varphi \vee \chi )}=\frac{{\mathcal {P}}(\chi \wedge \psi |\varphi \vee \chi )}{{\mathcal {P}}(\chi \wedge \psi |\varphi \vee \chi ) +{\mathcal {P}}(\chi \wedge \lnot \psi |\varphi \vee \chi )}$, and

• 3. ${\mathcal {P}}(\psi | \varphi \vee \chi )= {\mathcal {P}}(\psi \wedge (\chi \wedge \varphi ) |\varphi \vee \chi ) +{\mathcal {P}}(\psi \wedge (\lnot \chi \wedge \varphi ) |\varphi \vee \chi ) + {\mathcal {P}}(\psi \wedge (\chi \wedge \lnot \varphi ) |\varphi \vee \chi )$.

To simplify the proof, we represent the conditional probabilities on $\varphi \vee \chi$ by using the diagram in Fig. 3, similar to the one in the proof for CSO.

Fig. 3

Diagram for the Popper function ${\mathcal {P}}(\cdot | \varphi \vee \chi )$

Then, by Definition 1.4, we have

• 4. ${\mathcal {P}}(\varphi \wedge \psi |\varphi \vee \chi )=\underbrace{{\mathcal {P}}((\varphi \wedge \psi )\wedge \chi |\varphi \vee \chi )}_{t} + \underbrace{{\mathcal {P}}((\varphi \wedge \psi )\wedge \lnot \chi |\varphi \vee \chi )}_{w},$

• 5. ${\mathcal {P}}(\varphi \wedge \lnot \psi |\varphi \vee \chi )=\underbrace{{\mathcal {P}}((\varphi \wedge \lnot \psi ) \wedge \chi |\varphi \vee \chi )}_{y} + \underbrace{{\mathcal {P}}((\varphi \wedge \lnot \psi )\wedge \lnot \chi |\varphi \vee \chi )}_{x},$

• 6. ${\mathcal {P}}(\chi \wedge \psi |\varphi \vee \chi )=\underbrace{{\mathcal {P}}((\chi \wedge \psi )\wedge \varphi |\varphi \vee \chi )}_{t} + \underbrace{{\mathcal {P}}((\chi \wedge \psi )\wedge \lnot \varphi |\varphi \vee \chi )}_{k},$

• 7. ${\mathcal {P}}(\chi \wedge \lnot \psi |\varphi \vee \chi )=\underbrace{{\mathcal {P}}((\chi \wedge \lnot \psi )\wedge \varphi |\varphi \vee \chi )}_{y} + \underbrace{{\mathcal {P}}((\chi \wedge \lnot \psi )\wedge \lnot \varphi |\varphi \vee \chi )}_{z},$

Again by Definition 1.3 and 1.4, we have that $1={\mathcal {P}}(\varphi \vee \chi | \varphi \vee \chi )=x+y+z+t+k+w$. Then, simple calculations show that ${\mathcal {U}}(\varphi \rightarrow \psi )=\frac{x+y}{x+y+w+t}$, ${\mathcal {U}}( \chi \rightarrow \psi )= \frac{z+y}{t+k+z+y}$, and ${\mathcal {U}}((\varphi \vee \chi ) \rightarrow \psi )=x+y+z.$ Then, since $\frac{x+y}{x+y+w+t}\ge x+y$ and $\frac{z+y}{t+k+z+y}\ge z$, we obtain that $\frac{x+y}{x+y+w+t} +\frac{z+y}{t+k+z+y}\ge x+y+z$. That is, ${\mathcal {U}}(\varphi \rightarrow \psi )+{\mathcal {U}}( (\chi \rightarrow \psi )\ge {\mathcal {U}}((\varphi \vee \chi ) \rightarrow \psi )$.

Modus Ponens: $\varphi , \varphi \rightarrow \psi \vdash \psi$

t-valid: Modus Ponens is vacuously t-valid since the conclusion is not a conditional.

p-valid: Now suppose that T is a singleton.

Case 1: ${\mathcal {P}}(\varphi | \top )=0$:

Then, ${\mathcal {U}}(\varphi |\top )=1$. Therefore, ${\mathcal {U}}(\varphi )+{\mathcal {U}}(\varphi \rightarrow \psi )\ge 1\ge {\mathcal {U}}(\psi )$.

Case 2: ${\mathcal {P}}(\varphi | \top )\ne 0$:

Then, ${\mathcal {P}}(\psi |\varphi )=\frac{{\mathcal {P}}(\varphi \wedge \psi |\top )}{{\mathcal {P}}(\varphi |\top )}=\frac{{\mathcal {P}}(\varphi \wedge \psi |\top )}{{\mathcal {P}}(\varphi \wedge \psi |\top ) + {\mathcal {P}}(\varphi \wedge \lnot \psi |\top )}$. Moreover, by Definition 1.4, we have

• 1. $1={\mathcal {P}}(\top | \top )=\underbrace{{\mathcal {P}}(\varphi \wedge \psi |\top )}_{x} + \underbrace{{\mathcal {P}}(\lnot \varphi \wedge \psi |\top )}_{y} +\underbrace{{\mathcal {P}}(\varphi \wedge \lnot \psi |\top )}_{z} + \underbrace{{\mathcal {P}}(\lnot \varphi \wedge \lnot \psi |\top )}_{w},$

• 2. ${\mathcal {P}}(\varphi | \top )={\mathcal {P}}(\varphi \wedge \psi |\top )+{\mathcal {P}}(\varphi \wedge \lnot \psi |\top )=x+z,$ and

• 3. ${\mathcal {P}}(\psi | \top )={\mathcal {P}}(\varphi \wedge \psi |\top )+{\mathcal {P}}(\lnot \varphi \wedge \psi |\top )=x+y.$

Therefore, ${\mathcal {P}}(\psi |\varphi )=\frac{x}{x+z}$. Then, by simple calculations, we obtain that ${\mathcal {U}}(\varphi )+{\mathcal {U}}(\varphi \rightarrow \psi )=y+w+\frac{z}{x+z}\ge z+w = {\mathcal {U}}(\psi )$ (since $\frac{z}{x+z}\ge z$).

1.2 Proof of Theorem 3.2

MOD: $\lnot \varphi \rightarrow \varphi \vdash \psi \rightarrow \varphi$

p-validity: Let ${\mathcal {P}}$ be a Popper function and ${\mathcal {T}}=\langle T, \oplus , t, f \rangle$ be a singleton topic model on ${\mathcal {L}}_{PL}$. Since ${\mathcal {T}}$ is a singleton topic model, $\psi \rightarrow \varphi$ is an on-topic conditional wrt ${\mathcal {T}}$. We then have two cases:

Case 1: $\lnot \varphi$ is normal

Then, ${\mathcal {P}}(\varphi |\lnot \varphi )=0$. Therefore, ${\mathcal {U}}(\lnot \varphi \rightarrow \varphi )=1-{\mathcal {P}}(\varphi |\lnot \varphi )=1$. Since ${\mathcal {U}}(\psi \rightarrow \varphi )\in [0, 1]$, we obtain the result.

Case 2: $\lnot \varphi$ is abnormal

Then, ${\mathcal {P}}(\varphi |\lnot \varphi )=1$, thus, ${\mathcal {U}}(\lnot \varphi \rightarrow \varphi )=0$. Since ${\mathcal {T}}$ is a singleton model, we have ${\mathcal {U}}(\psi \rightarrow \varphi )=1-{\mathcal {P}}(\varphi |\psi )$. If $\psi$ is abnormal, then ${\mathcal {P}}(\varphi |\psi )=1$, thus, ${\mathcal {U}}(\psi \rightarrow \varphi )=0$. If $\psi$ is normal, then ${\mathcal {U}}(\psi \rightarrow \varphi )={\mathcal {P}}(\lnot \varphi |\psi )$ (by Lemma 4.1). Since $\lnot \varphi$ is abnormal, we have that ${\mathcal {P}}(\lnot \varphi |\psi )=0$, i.e., ${\mathcal {U}}(\psi \rightarrow \varphi )=0$.

t-invalidity: Consider the instance $\lnot p\rightarrow p \vdash q\rightarrow p$ and the topic model $\langle \{a, b\}, \oplus , t, f\rangle$ such that $\oplus$ is idempotent and $a\oplus b=a$, thus, $b\sqsubset a$. Moreover, f is a constant function and $t_q=b$ and $t_p=a$. Therefore, $a=t_p=f(t_{\lnot p})$ but $a=t_p\not \sqsubseteq f(t_q)=b$ (see Fig. 4).

Fig. 4

Topic model $\langle \{a, b\}, \oplus , t, f\rangle$

RCE: If $\varphi \vdash _{PL}\psi$, then $\vdash \varphi \rightarrow \psi$

p-validity: Follows immediately from Definition 1.3

t-invalidity: Consider the counterexample given in Fig. 4 and take $\varphi := q$ and $\psi : p\vee \lnot p$.

RCEA: If $\vdash _{PL}\varphi \equiv \psi$, then $\varphi \rightarrow \chi \dashv \vdash \psi \rightarrow \chi$

p-validity: Follows immediately from Definition 1.2.

t-invalidity: Consider the counterexample given in Fig. 4 and take $\varphi := p\vee \lnot p$, $\psi :=q\vee \lnot q$, $\chi :=r\vee \lnot r$ such that $t_r=a$. We then have that $\vDash _{PL} \varphi \equiv \psi$, $(p\vee \lnot p) \rightarrow (r\vee \lnot r)$ is an on-topic conditional wrt ${\mathcal {T}}$ but $(q\vee \lnot q) \rightarrow (r\vee \lnot r)$ is not.

RCEC: If $\vdash _{PL} \varphi \equiv \psi$, then $\chi \rightarrow \varphi \dashv \vdash \chi \rightarrow \psi$

p-validity: Follows immediately from Lemma 4.2.

t-invalidity: Consider the counterexample above but set $t_p=t_r=b$ and $t_q=a$.

RCK: If $\vdash _{PL}(\varphi _1\wedge \dots \wedge \varphi _n)\supset \psi$, then $\chi \rightarrow \varphi _1, \dots , \chi \rightarrow \varphi _n \vdash \chi \rightarrow \psi$

p-validity: Suppose that ${\mathcal {T}}$ is a singleton topic model and $\vdash _{PL}(\varphi _1\wedge \dots \wedge \varphi _n)\supset \psi$. We want to show that ${\mathcal {U}}(\chi \rightarrow \varphi _1)+\dots +{\mathcal {U}}(\chi \rightarrow \varphi _n)\ge {\mathcal {U}}(\chi \rightarrow \psi )$, i.e., that $1-{\mathcal {P}}(\varphi _1|\chi ) + \dots +1-{\mathcal {P}}(\varphi _n|\chi )\ge 1-{\mathcal {P}}(\psi |\chi )$, i.e., that ${\mathcal {P}}(\psi |\chi )\ge {\mathcal {P}}(\varphi _1|\chi ) + \dots {\mathcal {P}}(\varphi _n|\chi )-n+1$. It is easy to see that

$$\begin{aligned} {\mathcal {P}}(\psi |\chi )&\ge {\mathcal {P}}(\varphi _1\wedge \dots \wedge \varphi _n|\chi ) \qquad (\text {by the assumption and Lemma}\,4.\text {3})\\&\ge {\mathcal {P}}(\varphi _1|\chi ) + \dots {\mathcal {P}}(\varphi _n|\chi )-n+1 \qquad (\text {by repeated applications of Lemma}\,4.\text {4}) \end{aligned}$$

t-invalidity: Same as the proof of RCEC.

RCM: $\vdash _{PL}\varphi \supset \psi$, then $\chi \rightarrow \varphi \vdash \chi \rightarrow \psi$

p-validity: Follows immediately by Lemma 4.3.

t-invalidity: Same as the proof of RCEC.

And-to-If: $\varphi \wedge \psi \vdash \varphi \rightarrow \psi$

p-validity: Let ${\mathcal {P}}$ be a Popper function and ${\mathcal {T}}$ be a singleton topic model. Then, ${\mathcal {U}}(\varphi \wedge \psi )=1-{\mathcal {P}}(\varphi \wedge \psi | \top )$ and ${\mathcal {U}}(\varphi \rightarrow \psi )=1-{\mathcal {P}}(\psi | \varphi )$. If ${\mathcal {P}}(\varphi |\top )=0$, then ${\mathcal {P}}(\varphi \wedge \psi | \top )=0$ (by Lemma 4.3). Therefore, ${\mathcal {U}}(\varphi \wedge \psi )=1 \ge {\mathcal {U}}(\varphi \rightarrow \psi )$. If ${\mathcal {P}}(\varphi |\top )\ne 0$, then ${\mathcal {P}}(\psi | \varphi )=\frac{{\mathcal {P}}(\varphi \wedge \psi | \top )}{{\mathcal {P}}(\varphi |\top )}$. Thus, since ${\mathcal {P}}(\varphi |\top )\in [0, 1]$, we obtain that ${\mathcal {P}}(\psi | \varphi )\ge {\mathcal {P}}(\varphi \wedge \psi | \top )$. Thefore, ${\mathcal {U}}(\varphi \wedge \psi ) \ge {\mathcal {U}}(\varphi \rightarrow \psi )$.

t-invalidity: See the counterexample given in Fig. 4 and take $\varphi := q$ and $\psi :=p$.

1.3 Proof of Theorem 3.3

We prove Theorems 3.3 and 3.4 by showing that every inference $\Gamma \vdash \Delta$ that is invalid with respect to AT and Adams’ notion of probabilistic validity is also p-invalid with respect to our proposal. Let us first recall Adams’ framework and fix notation (Adams 1998). The reader who is familiar with Adams’ probabilistic conditional logic and the connection between Popper and unconditional probability functions should feel free to skip until Corollary 6.

Let $\mathrm{p}:{\mathcal {L}}\rightarrow [0,1]$ be a(n) (unconditional) probability function defined on the language ${\mathcal {L}}$ such that for all $\varphi , \psi \in {\mathcal {L}}_{PL}$, $\mathrm{p}(\varphi )$ and $\mathrm{p}(\psi )$ satisfy the Kolmogorov axioms and

$$\begin{aligned} \mathrm{p}(\varphi \rightarrow \psi )={\left\{ \begin{array}{ll} \frac{\mathrm{p}(\psi \wedge \varphi )}{\mathrm{p}(\varphi )}, &{} \text{ if } \mathrm{p}(\varphi )\ne 0\\ 1 &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

The corresponding uncertainty function $\mathrm{u}_\mathrm{p}:{\mathcal {L}}\rightarrow [0,1]$ is defined as $\mathrm{u}_\mathrm{p}(\varphi )=1-\mathrm{p}(\varphi )$ for all $\varphi \in {\mathcal {L}}$ (see Adams 1998, Chapters 6 & 7). In fact, every unconditional probability measure $\mathrm{p}$ on ${\mathcal {L}}$ leads to a Popper function ${\mathcal {P}}_\mathrm{p}: {\mathcal {L}}_{PL}\times {\mathcal {L}}_{PL}\rightarrow [0,1]$ defined as ${\mathcal {P}}_\mathrm{p}(\psi | \varphi )= \mathrm{p}(\varphi \rightarrow \psi )$, for all $\varphi , \psi \in {\mathcal {L}}_{PL}$. The following lemma proves this result, which will be useful in proving Theorems 3.3 and 3.4.

Lemma 5

Given an unconditional probability function $\mathrm{p}:{\mathcal {L}}\rightarrow [0,1]$, the conditional probability measure ${\mathcal {P}}_\mathrm{p}: {\mathcal {L}}_{PL}\times {\mathcal {L}}_{PL}\rightarrow [0,1]$ defined as ${\mathcal {P}}_\mathrm{p}(\psi | \varphi )= \mathrm{p}(\varphi \rightarrow \psi )$ is a Popper function.

Proof

We need to show that ${\mathcal {P}}_\mathrm{p}$ satisfies the conditions given in Definition 1.

• 1. By the definition of $\mathrm{p}$, we know that $\mathrm{p}(\top )=1$ and $\mathrm{p}(\bot )=0$. Therefore, ${\mathcal {P}}_\mathrm{p}(\bot |\top )=\frac{\mathrm{p}(\bot \wedge \top )}{\mathrm{p}(\top )}=\frac{0}{1}=0\ne 1$.

Let $\varphi , \psi , \chi \in {\mathcal {L}}_{PL}$.

• 2. Suppose that $\vDash _{PL} \psi \equiv \chi$. Then, by classical propositional logic, we know that $\vDash _{PL} (\psi \wedge \varphi ) \equiv (\chi \wedge \varphi )$. By the properties of $\mathrm{p}$, we also have that $\mathrm{p}(\psi )=\mathrm{p}(\chi )$ and $\mathrm{p}(\psi \wedge \varphi )=\mathrm{p}(\chi \wedge \varphi )$. Hence,

  $$\begin{aligned} {\mathcal {P}}_\mathrm{p}(\varphi | \psi )= {\left\{ \begin{array}{ll} \frac{\mathrm{p}(\psi \wedge \varphi )}{\mathrm{p}(\psi )}, &{} \text{ if } \mathrm{p}(\psi )\ne 0\\ 1 &{} \text{ otherwise }\end{array}\right. }={\mathcal {P}}_\mathrm{p}(\varphi | \chi ) = {\left\{ \begin{array}{ll} \frac{\mathrm{p}(\chi \wedge \varphi )}{\mathrm{p}(\chi )}, &{} \text{ if } \mathrm{p}(\chi )\ne 0\\ 1 &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

• 3. Suppose that $\varphi \vDash _{PL} \psi$. Then, by classical propositional logic, we know that $\vDash _{PL} (\varphi \wedge \psi )\equiv \varphi$. Therefore, by the properties of $\mathrm{p}$, we have that $\mathrm{p}(\varphi \wedge \psi )=\mathrm{p}(\varphi )$. Hence, in both cases where $\mathrm{p}(\varphi )\ne 0$ and $\mathrm{p}(\varphi ) =0$, we have ${\mathcal {P}}_\mathrm{p}(\psi | \varphi )=1$.

• 4. Suppose that $\varphi \vDash _{PL} \lnot (\psi \wedge \chi )$. We have two cases:

  Case 1: $\mathrm{p}(\varphi )=0$

  Then, by the definition of ${\mathcal {P}}_\mathrm{p}$, we know that ${\mathcal {P}}(\eta |\varphi )=1$ for all $\eta \in {\mathcal {L}}_{PL}$.

  Case 2: $\mathrm{p}(\varphi )\ne 0$

  Then,

  $$\begin{aligned} {\mathcal {P}}_\mathrm{p}(\psi \vee \chi |\varphi )&=\frac{\mathrm{p}((\psi \vee \chi )\wedge \varphi )}{\mathrm{p}(\varphi )} \qquad (\text {by the defn. of}\ {\mathcal {P}}_\mathrm{p})\\&= \frac{\mathrm{p}((\psi \wedge \varphi ) \vee (\chi \wedge \varphi ))}{\mathrm{p}(\varphi )}\\&\qquad (\text {since}\ \vDash _{PL}((\psi \vee \chi )\wedge \varphi )\equiv ((\psi \wedge \varphi ) \vee (\chi \wedge \varphi )))\\&= \frac{\mathrm{p}(\psi \wedge \varphi ) + \mathrm{p}(\chi \wedge \varphi )}{\mathrm{p}(\varphi )} \qquad (\text {since}\ \vDash _{PL}\lnot ((\psi \wedge \varphi ) \wedge (\chi \wedge \varphi )))\\&= \frac{\mathrm{p}(\psi \wedge \varphi )}{\mathrm{p}(\varphi )} + \frac{\mathrm{p}(\chi \wedge \varphi )}{\mathrm{p}(\varphi )}\\&= {\mathcal {P}}_\mathrm{p}(\psi |\varphi )+ {\mathcal {P}}_\mathrm{p}(\chi |\varphi ) \qquad (\text {by the defn. of}\ {\mathcal {P}}_\mathrm{p}) \end{aligned}$$

• 5. We have two cases:

  Case 1: $\mathrm{p}(\varphi )=0$

  Then, by the properties of $\mathrm{p}$, $\mathrm{p}(\psi \wedge \varphi )=0$. Therefore, $1={\mathcal {P}}_\mathrm{p}(\psi \wedge \chi | \varphi )={\mathcal {P}}_\mathrm{p}(\psi |\varphi ){\mathcal {P}}_\mathrm{p}(\chi |\psi \wedge \varphi )$.

  Case 2: $\mathrm{p}(\varphi )\ne 0$

  Then, ${\mathcal {P}}_\mathrm{p}(\psi \wedge \chi | \varphi )=\frac{\mathrm{p}(\psi \wedge \chi \wedge \varphi )}{\mathrm{p}(\varphi )}$ and ${\mathcal {P}}_\mathrm{p}(\psi | \varphi )=\frac{\mathrm{p}(\psi \wedge \varphi )}{\mathrm{p}(\varphi )}$. Then, if $\mathrm{p}(\psi \wedge \varphi )=0$, we have $0={\mathcal {P}}_\mathrm{p}(\psi \wedge \chi | \varphi )={\mathcal {P}}_\mathrm{p}(\psi |\varphi ){\mathcal {P}}_\mathrm{p}(\chi |\psi \wedge \varphi )$. If $\mathrm{p}(\psi \wedge \varphi )\ne 0$, we obtain that ${\mathcal {P}}_\mathrm{p}(\chi | \psi \wedge \varphi )=\frac{\mathrm{p}(\psi \wedge \chi \wedge \varphi )}{\mathrm{p}( \psi \wedge \varphi )}$. Therefore,

  $$\begin{aligned} {\mathcal {P}}_\mathrm{p}(\psi |\varphi ){\mathcal {P}}_\mathrm{p}(\chi |\psi \wedge \varphi )&= \frac{\mathrm{p}(\psi \wedge \varphi )}{\mathrm{p}(\varphi )} \cdot \frac{\mathrm{p}(\psi \wedge \chi \wedge \varphi )}{\mathrm{p}( \psi \wedge \varphi )}\\&= \frac{\mathrm{p}(\psi \wedge \chi \wedge \varphi )}{\mathrm{p}(\varphi )}\\&={\mathcal {P}}_\mathrm{p}(\psi \wedge \chi | \varphi ). \end{aligned}$$

$\square$

Corollary 6

Given an unconditional probability function $\mathrm{p}:{\mathcal {L}}\rightarrow [0,1]$, a topic model ${\mathcal {T}}=\langle T, \oplus , t, f \rangle$ on ${\mathcal {L}}_{PL}$ with T a singleton, and $\varphi \in {\mathcal {L}}$, we have ${\mathcal {U}}_{{\mathcal {P}}_\mathrm{p}, {\mathcal {T}}}(\varphi )=u_\mathrm{p}(\varphi )$, where ${\mathcal {U}}_{{\mathcal {P}}_\mathrm{p}, {\mathcal {T}}}$ is the degree of unacceptability as given in Definition 3.

Proof

Observe that, since T is singleton, we have $t_\psi =f(t_\varphi )$ for all $\varphi , \psi \in {\mathcal {L}}_{PL}$. Therefore,

$$\begin{aligned} {\mathcal {U}}_{{\mathcal {P}}_\mathrm{p}, {\mathcal {T}}}(\varphi )={\left\{ \begin{array}{ll} 1-{\mathcal {P}}_\mathrm{p}(\chi |\psi ), &{} \text{ if } \varphi := \psi \rightarrow \chi , \\ 1-{\mathcal {P}}_\mathrm{p}(\varphi |\top ) &{} \text{ if } \varphi \in {\mathcal {L}}_{PL}. \end{array}\right. } \end{aligned}$$

Then, by the definition of ${\mathcal {P}}_\mathrm{p}$, we obtain that

$$\begin{aligned} {\mathcal {U}}_{{\mathcal {P}}_\mathrm{p}, {\mathcal {T}}}(\varphi )={\left\{ \begin{array}{ll} 1-\mathrm{p}(\psi \rightarrow \chi ), &{} \text{ if } \varphi := \psi \rightarrow \chi , \\ 1-\mathrm{p}(\top \rightarrow \varphi ) &{} \text{ if } \varphi \in {\mathcal {L}}_{PL}. \end{array}\right. } \end{aligned}$$

It is easy to see that $\mathrm{p}(\top \rightarrow \varphi )=\mathrm{p}(\varphi )$. Therefore, by the definition of $\mathrm{u}_\mathrm{p}$, we conclude that ${\mathcal {U}}_{{\mathcal {P}}_\mathrm{p}, {\mathcal {T}}}(\varphi )=\mathrm{u}_\mathrm{p}(\varphi )$. $\square$

For the sake of the following argument, we call Adams’ probabilistic (in)validity defined in (Adams 1998, p. 151) A-(in)validity.

Corollary 7

Any A-invalid principle $\Gamma \vdash \Delta$ is also p-invalid.

Proof

Let $\Gamma \vdash \Delta$ be an A-invalid inference. This means that there is an unconditional probability measure $\mathrm{p}:{\mathcal {L}}\rightarrow [0,1]$ and a corresponding uncertainty function $\mathrm{u}_\mathrm{p}:{\mathcal {L}}\rightarrow [0,1]$ such that $\sum \limits _{\varphi \in \Gamma } \mathrm{u}_\mathrm{p}(\varphi )< \mathrm{u}_\mathrm{p}(\psi ),$ for some $\psi \in \Delta$. Then, by Corollary 6, we obtain that $\sum \limits _{\varphi \in \Gamma }{\mathcal {U}}_{{\mathcal {P}}_\mathrm{p}, {\mathcal {T}}}(\varphi ) <{\mathcal {U}}_{{\mathcal {P}}_\mathrm{p}, {\mathcal {T}}}(\psi ),$ where ${\mathcal {U}}_{{\mathcal {P}}_\mathrm{p}, {\mathcal {T}}}$ is the degree of unacceptability wrt ${\mathcal {P}}_\mathrm{p}$ and some ${\mathcal {T}}=\langle T, \oplus , t, f \rangle$ with a singleton T. $\square$

Proof of Theorem 3.3

p-invalidity of Trans and SA follow from Corollary 7 since they are also A-invalid, as shown in (Adams 1998, p. 125-126).

t-validity:

Trans: $\varphi \rightarrow \psi , \psi \rightarrow \chi \vdash \varphi \rightarrow \chi$

Suppose that $t_\psi \sqsubseteq f(t_\varphi )$ and $t_\chi \sqsubseteq f(t_\psi )$. The former, by Lemma 1 and Definition 2.4b, implies that $f(t_\psi ) \sqsubseteq f(t_\varphi )$. Since $\sqsubseteq$ is transitive, by the latter, we obtain that $t_\chi \sqsubseteq f(t_\varphi )$.

SA: $\varphi \rightarrow \psi \vdash (\varphi \wedge \chi )\rightarrow \psi$

Suppose that $t_\psi \sqsubseteq f(t_\varphi )$. Then, since $t_\varphi \sqsubseteq t_{\varphi \wedge \chi }$, we obtain that $f(t_\varphi )\sqsubseteq f(t_{\varphi \wedge \chi })$ (by Lemma 1). Since $\sqsubseteq$ is transitive, we conclude that $t_\psi \sqsubseteq f(t_{\varphi \wedge \chi })$. $\square$

1.4 Proof of Theorem 3.4

p-invalidity of Or-to-If, Contraposition, and SDA follow from Corollary 7 since they are also A-invalid. See (Adams 1998, p. 121) for the A-invalidity of Or-to-if and Contraposition and (Adams 1998, p. 331, counterexample-e) for the A-invalidity of SDA.

t-invalidity:

For Or-to-If and Contraposition, consider the topic model given in Fig. 4. This model t-invalidates Or-to-If since $q\vee p$ is not a conditional and $\lnot q \rightarrow p$ is not an on-topic conditional wrt ${\mathcal {T}}$: $a=t_{p}\not \sqsubseteq f(t_{\lnot q})=b$. And, it t-invalidates Contraposition since $p\rightarrow \lnot q$ is an on-topic conditional wrt ${\mathcal {T}}$ (since $b=t_{\lnot q} \sqsubseteq f(t_{p})=a$) but $q\rightarrow \lnot p$ is not (since $a=t_{\lnot p}\not \sqsubseteq f(t_q)=b$). For SDA, consider the topic model ${\mathcal {T}}'=\langle \{a, b, c\}, \oplus ', f', t'\rangle$ where $\oplus '$ is as depicted in Fig. 5, $f'$ is a constant function, and $t'_p=b$, $t'_q=c$, and $t'_r=a$. It is then easy to see that $(p\vee q) \rightarrow r$ is an on-topic conditional wrt ${\mathcal {T}}$, however, neither $p\rightarrow r$ nor $q\rightarrow r$ is.

Fig. 5

Counterexample for the t-invalidity of SDA

1.5 Proof of Theorem 3.5

That Trans, SA, Or-to-If, Contraposition, and SDA are invalid follows from Lemma 2, Theorems 3.3, and 3.4. For RCE, RCEA, RCEC, RCK, and RCM, the counter-topic models given in the proof of Theorem 3.2 together with any arbitrary Popper function constitute counterexamples for their validity, respectively, since in each case the degree of unacceptability of the elements in $\Gamma$ is 0 and the degree of unacceptability of the elements in $\Delta$ is 1 (since the conditionals in $\Delta$ are off-topic conditionals with respect to the corresponding topic models). For And-to-If, consider the instance $q\wedge p \vdash q\rightarrow p$. This is invalidated by the topic model given in Fig. 4 together with any Popper function ${\mathcal {P}}$ such that ${\mathcal {P}}(p\wedge q | \top )\ne 0$. Finally, MOD is invalid only when $\lnot \varphi$ is abnormal. Consider the instance $\lnot (p\vee \lnot p)\rightarrow (p \vee \lnot p)\vdash q\rightarrow (p\vee \lnot p)$. Observe that, for any Popper function ${\mathcal {P}}$, we have (by Definition 1.3), ${\mathcal {P}}(p \vee \lnot p| \lnot (p\vee \lnot p))=1$. Consider also the topic model given in Fig. 4. Then, we have that ${\mathcal {U}}(\lnot (p\vee \lnot p)\rightarrow (p \vee \lnot p))=1-{\mathcal {P}}(p \vee \lnot p| \lnot (p\vee \lnot p))=0$. However, as $t_{p\vee \lnot p}\not \sqsubseteq f(t_q)$, we have ${\mathcal {U}}(q\rightarrow (p\vee \lnot p))=1$. Therefore, ${\mathcal {U}}(\lnot (p\vee \lnot p)\rightarrow (p \vee \lnot p))<{\mathcal {U}}_{{\mathcal {P}}, {\mathcal {T}}}(q\rightarrow (p\vee \lnot p))$.