Skip to main content
SpringerLink
Log in

Spatiotemporal deformation of multi-soliton to (2 + 1)-dimensional KdV equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

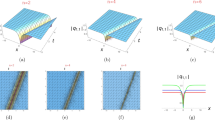
This work proposes a three-wave method with a perturbation parameter to obtain exact multi-soliton solutions of nonlinear evolution equation. The (\(2+1\))-dimensional KdV equation is used as an example to illustrate the effectiveness of the suggested method. Using this method, new multi-soliton solutions are given. Specially, spatiotemporal dynamics of breather two-soliton and multi-soliton including deformation between bright and dark multi-soliton each other, and deflection with different directions and angles are investigated and exhibited to (\(2+1\))D KdV equation. Some new nonlinear phenomena are revealed under the small perturbation of parameter.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Zabusky, N.J., Kruskal, M.D.: Interaction of solitons in a collisionaless plasma and the recurrence of initial states. Phys. Rev. Lett. 15, 240–243 (1965)

    Article  MATH  Google Scholar 

  2. Ablowitz, M.J., Clarkson, P.A.: Solitons, nonlinear evolution equations and inverse scattering, vol. 149. Cambridge University Press, Cambridge (1999)

    MATH  Google Scholar 

  3. Weiss, J., Tabor, M., Carnevale, G.: The Painlevé property for partial differential equation. J. Math. Phys. 24, 522 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  4. Pogrebkov, A.K.: On the formulation of the Painlevé test as a criterion of complete integrability of partial differential equation. Inverse Probl. 5(1), L7–L10 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  5. Weiss, J.: The Painlevé property for partial differential equations, II: Bäcklund transformation, Lax pairs, and the Schwarzian derivative. J. Math. Phys. 24, 1405 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  6. Steeb, W.H., Kloke, M., Spieker, B.M.: Liouville equation, Painlevé property and Bäcklund transformation. Z. Naturforsch. A 38, 1054–1055 (1983)

    MathSciNet  MATH  Google Scholar 

  7. Weiss, J.: The sine-Gordon equations: complete and partial integrability. J. Math. Phys. 25, 2226 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  8. Musette, M., Conte, R.: Algorithmic method for deriving Lax pairs from the invariant Painlevé analysis of nonlinear partial differential equations. J. Math. Phys. 32, 1450–1457 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  9. Lou, S.Y.: Searching for higher dimensional integrable models from lower ones via Painlevé analysis. Phys. Rev. Lett. 80, 5027 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  10. Ma, W.X., Huang, T.W., Zhang, Y.: A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 82, 065003 (2010)

    Article  MATH  Google Scholar 

  11. Ma, W.X., Fan, E.G.: Linear superposition principle applying to Hirota bilinear equations. Comput. Math. Appl. 61, 950–959 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  12. Ma, W.X.: Complexiton solutions to the Korteweg–de Vries equation. Phys. Lett. A 301, 35–44 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Ma, W.X., You, Y.: Solving the Korteweg–de Vries equation by its bilinear form: Wronskian solutions. Trans. Am. Math. Soc. 357, 1753–1778 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  14. Qin, Z.Y.: On periodic wave solution and asymptotic property of KdV–Sawada–Kotera equation. J. Phys. Soc. Jpn. B 76, 124004 (2007)

    Article  Google Scholar 

  15. Tang, X.Y., Lou, S.Y., Zhang, Y.: Localized excitations in (2 + 1)-dimensional systems. Phys. Rev. E 66, 046601 (2002)

    Article  MathSciNet  Google Scholar 

  16. Meng, J.P., Zhang, J.F.: Nonpropagating solitary waves in (2 + 1)-dimensional nonlinear systems. Commun. Theor. Phys. 43, 831–836 (2005)

    Article  MathSciNet  Google Scholar 

  17. Zheng, C.L., Fang, J.P., Chen, L.Q.: New variable separation excitations of (2 + 1)-dimensional dispersive long-water wave system obtained by an extended mapping approach. Chaos Solitons Fractals 23, 1741–1748 (2005)

    MathSciNet  MATH  Google Scholar 

  18. Fu, H.M., Dai, Z.D.: Double exp-function method and application. Int. J. Nonlinear Sci. Numer. Simul. 10(7), 927–934 (2009)

    Article  Google Scholar 

  19. Lou, S.Y.: Symmetries and algebras of the integrable dispersive long wave equations in (2 + 1)-dimensional spaces. J. Phys. A Math. 27, 3235 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  20. Wang, J.W., Li, H.X., Wu, H.N.: Distributed proportional plus second-order spatial derivative control for distributed parameter systems subject to spatiotemporal uncertainties. Nonlinear Dyn. 76(4), 2041–2058 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  21. Jiang, Y., Tian, B., Liu, W.J.: Solitons, Bäcklund transformation and Lax pair for the (2 + 1)-dimensional Boiti–Leon–Pempinelli equation for the water waves. J. Math. Phys. 51(9), 093519–093519-11 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  22. Liu, W.J., Lei, M.: Types of coefficient constraints of coupled nonlinear Schrödinger equations for elastic and inelastic interactions between spatial solitons with symbolic computation. Nonlinear Dyn. 76(4), 1935–1941 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  23. Peng, Y.Z., Krishnan, E.V.: The singular manifold method and exact periodic wave solutions to a restricted BLP dispersive long wave system. Rep. Math. Phys. 56(3), 367–378 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  24. Rosenau, P.: Nonlinear dispersion and compact structures. Phys. Rev. Lett. 73, 1737–1741 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  25. Garagash, T.I.: Modification of the Painlevé test for systems of nonlinear partial differential equations. Theor. Math. Phys. 100, 1075 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  26. Boiti, M., Leon, J.P., Manna, M., Pempinelli, F.: On the spectral transform of a Korteweg–de Vries equation in two spatial dimensions. Inverse Probl. 2, 271–279 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  27. Dorizzi, B., Grammaticos, B., Ramani, A., Winternitz, P.: Are all the equations of the Kadomtsev–Petviashvili hierarchy integrable? J. Math. Phys. 27, 2848 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  28. Tamizhmani, K.M., Punithavathi, P.: The infinite-dimensional lie algebraic structure and the symmetry reduction of a nonlinear higher-dimensional equation. J. Phys. Soc. Jpn. 59, 843–847 (1990)

    Article  MathSciNet  Google Scholar 

  29. Peng, Y.Z.: New Bäcklund transformation and new exact solutions to (2 + 1)-dimensional KdV equation. Commun. Theor. Phys. (Beijing, China) 40, 257–258 (2003)

    Article  MATH  Google Scholar 

  30. Zhang, H., Ma, W.X.: Extended transformed rational function method and applications to complexiton solutions. Appl. Math. Comput. 230, 509–515 (2014)

    Article  MathSciNet  Google Scholar 

  31. Xu, Z., Chen, H., Jiang, M., Dai, Z., Chen, W.: Resonance and deflection of multi-soliton to the (2 + 1)-dimensional Kadomtsev–Petviashvili equation. Nonlinear Dyn. 78(1), 461–466 (2014)

    Article  MathSciNet  Google Scholar 

  32. Mirzazadeh, M., Eslami, M., Biswas, A.: 1-Soliton solution of KdV6 equation. Nonlinear Dyn. 80, 387–396 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  33. Razborova, P., Triki, H., Biswas, A.: Perturbation of dispersive shallow water waves. Ocean Eng. 63, 1–7 (2013)

    Article  Google Scholar 

  34. Razborova, P., Kara, A.H., Biswas, A.: Additional conservation laws for Rosenau–KdV–RLW equation with power law nonlinearity by Lie symmetry. Nonlinear Dyn. 79(1), 743–748 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  35. Biswas, A.: Solitary wave solution for KdV equation with power law nonlinearity and time-dependent coefficients. Nonlinear Dyn. 58, 345–348 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  36. Bhrawy, A.H., Abdelkawy, M.A., Biswas, A.: Cnoidal and snoidal wave solutions to coupled nonlinear wave equations by the extended Jacobi’s elliptic function method. Commun. Nonlinear Sci. Numer. Simul. 18, 915–925 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  37. Bhrawy, A.H., Biswas, A., Javidi, M., Ma, W.X., Pinar, Z., Yildirim, A.: New solutions for (1 + 1)-dimensional Kaup–Kuperschmidt equations. Results Math. 63, 675–686 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  38. Bhrawy, A.H., Abdelkawy, M.A., Kumar, S., Johnson, S., Biswas, A.: Solitons and other solutions to quantum Zakharov–Kuznetsov equation in quantum magneto-plasmas. Indian J. Phys. 87, 455–463 (2013)

    Article  Google Scholar 

  39. Bhrawy, A.H., Abdelkawy, M.A., Kumar, S., Biswas, A.: Solitons and other solutions to Kadomtsev–Petviashvili equation of B-type. Rom. J. Phys. 58, 729–748 (2013)

    MathSciNet  Google Scholar 

  40. Ebadi, G., Fard, N.Y., Bhrawy, A.H., Kumar, S., Triki, H., Yildirim, A., Biswas, A.: Solitons and other solutions to the (3 + 1)-dimensional extended Kadomtsev–Petviashvili equation with power law nonlinearity. Rom. Rep. Phys. 65, 27–62 (2013)

    Google Scholar 

  41. Biswas, A., Bhrawy, A.H., Abdelkawy, M.A., Alshaery, A.A., Hilal, E.M.: Symbolic computation of some nonlinear fractional differential equations. Rom. J. Phys. 59, 433–442 (2014)

    Google Scholar 

  42. Triki, H., Kara, A.H., Bhrawy, A., Biswas, A.: Soliton solution and conservation law of Gear–Grimshaw model for shallow water waves. Acta Phys. Pol. A 125, 1099–1106 (2014)

    Article  Google Scholar 

  43. Triki, H., Mirzazadeh, M., Bhrawy, A.H., Razborova, P., Biswas, A.: Soliton and other solutions to long-wave short wave interaction equation. Rom. J. Phys. 60, 72–86 (2015)

    Google Scholar 

  44. Bhrawy, A.H., Abdelkawy, M.A., Biswas, A.: Topological solitons and cnoidal waves to a few nonlinear wave equations in theoretical physics. Indian J. Phys. 87, 1125–1131 (2013)

    Article  Google Scholar 

Download references

Acknowledgments

The work was supported in part by the State Administration of Foreign Experts Affairs of China, the National Natural Science Foundation of China (No. 10801037, No.11361048), the New Teacher Grant of Ministry of Education of China (No.20080246), the Young Teachers Foundation (No. 1411018) of Fudan university and Qujin Normal University NSF Grant ( No.2010QN018).

Author information

Authors and Affiliations

  1. College of Mathematics and Information Science, Qujing Normal University, Qujing, 655011, People’s Republic of China

    Jun Liu, Gui Mu & Hongying Luo

  2. School of Mathematics and Statistics, Yunnan University, Kunming, 650091, People’s Republic of China

    Zhengde Dai

Authors
  1. Jun Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gui Mu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhengde Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hongying Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhengde Dai.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, J., Mu, G., Dai, Z. et al. Spatiotemporal deformation of multi-soliton to (2 + 1)-dimensional KdV equation. Nonlinear Dyn 83, 355–360 (2016). https://doi.org/10.1007/s11071-015-2332-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2332-6

Keywords

Search

Navigation