Proudman resonance with tides, bathymetry and variable atmospheric forcings

Abstract

Proudman resonance is a primary amplification mechanism for meteotsunamis, which are shallow-water waves generated by atmospheric forcings. The effect of tides, sloping bathymetry and the speed, amplitude and aspect ratio of the atmospheric forcing on Proudman resonant wave growth are investigated using analytical approximations and numerical models. With tides included, maximum wave growth through Proudman resonance occurred when the atmospheric-forcing speed matched the tidal-wave speed. Growth greater than Proudman resonance occurred with a positive tidal elevation together with a tidal current in the opposite direction to wave propagation, due to linear growth combined with further amplification from wave-flux conservation. Near-Proudman resonant growth occurred when the forced-wave speed or free-wave speed varied by either a small amount, or varied rapidly, around a speed appropriate for Proudman resonance. For a forcing moving at Proudman resonant speed, resultant wave growth was proportional to the total, time-integrated forcing amplitude. Finally, Proudman resonant wave growth was lower for forcings with lower aspect ratios (A_P), partly because forced-wave heights are proportional to 1 + A ²_P , but also because free waves could spread in two dimensions. Whilst the assumptions of strict Proudman resonance are never met, near-Proudman resonant growth may occur over hundreds of kilometres if the effective Froude number is near 1 and the resultant wave propagates predominantly in one dimension.

1 Introduction

Meteotsunamis are atmospherically generated, potentially dangerous, shallow-water waves with periods between 2 and 120 min (Monserrat et al. 2006). The wave amplification in meteotsunamis has been commonly attributed to Proudman resonance (e.g. Hibiya and Kajiura 1982; Monserrat et al. 2006), which occurs when the speed of an atmospheric pressure forcing matches the shallow-water wave speed (Proudman 1929). Shallow-water waves that are confined to one dimension x propagate as

$$ c\left( x \right) \approx \sqrt {gH(x)} + u_{c} \left( x \right), $$

(1)

where c(x) is the wave speed, g is the gravitational acceleration (here taken as 9.81 ms⁻²), H(x) is the water depth and u_c(x) is a background current. The net shallow-water wave speed increases with increasing depth and along-propagation currents and decreases with decreasing depth and counter-currents.

The assumptions used to construct strict Proudman resonance mean that the mathematical model is highly simplified compared to reality. Strict Proudman resonance has oceanographic assumptions of a still (u_c = 0), flat-bottomed, one-dimensional basin and atmospheric assumptions of a constant-speed, constant-amplitude, one-dimensional pressure forcing (Proudman 1929). There are also more fundamental physical assumptions: the ocean is frictionless, non-rotating and non-advecting, and the wave has negligible height. For such a modelled ocean, with an atmospheric pressure forcing P, moving at speed U in time t, the sea-level elevation, η, is

$$ \eta (x, t) = {-}\frac{1}{\rho g}\left\{ {\frac{{P\left( {x {-} Ut} \right)}}{{1 {-} \left( {U/c} \right)^{2} }}{-}\frac{{P\left( {x {-} ct} \right)}}{{2 \left( {1 {-} U/c} \right)}}{-}\frac{{P\left( {x + ct} \right)}}{{2 \left( {1 + U/c} \right)}}} \right\}, $$

(2)

where ρ is the water density. Equation 2 describes the sea-level elevation as the sum of a rightward forced wave (speed U), a rightward free wave of opposite sign (speed c), which both grow as U/c → 1, and a smaller leftward free wave (Levin and Nosov 2016). Typically, the Froude number Fr (Fr = U/c) is used to indicate when forced-wave and free-wave speeds match.

As Fr → 1, the physical separation between the rightward forced wave and rightward free wave decreases, until they are at an infinitesimally close superposition (Levin and Nosov 2016). Then, as x increases (whilst the superposition remains infinitesimally close), the sea-level elevation simplifies to

$$ \eta (x, t) \approx {-}\frac{x}{2\rho g}P_{x} , $$

(3)

where P = P(x − Ut) and the subscript x refers to partial differentiation in the along-propagation direction. The approximation in Eq. 3 (found by integrating equation A14 from Churchill et al. (1995), assuming that the initial wave height is negligible) shows three important wave characteristics. First, the resultant Proudman resonant wave grows linearly with distance moved. Second, the wave shape is that of the atmospheric pressure gradient. Third, the wave is scaled by − 1/ρg (inverted barometer effect). As the wave grows, eventually the assumption of negligible wave height is broken and linear wave growth stops (Levin and Nosov 2016).

Despite the rigid assumptions required for strict Proudman resonance, Proudman-like resonance can occur when these assumptions are not met. We consider two types of assumptions: oceanographic and atmospheric. Oceanographic assumptions considered here are the stillness and flat-bottom assumptions. Proudman-like resonance has been previously simulated in two-dimensional oceanographic models with tides and variable bathymetry (e.g. Choi et al. 2014; Williams et al. 2019). Atmospheric assumptions considered here are the constant forcing speed, constant forcing amplitude and one-dimensionality assumptions. Proudman resonance has been inferred (Wertman et al. 2014) and simulated (Anderson et al. 2015) for linear convective systems moving at varying speeds, with varying amplitude with two-dimensional surface pressure fields. A few case studies have attempted to discuss the effect on wave amplification when these multiple assumptions are unmet. Nevertheless, these case studies do not give much insight into underlying wave dynamics.

The purpose of this study is to determine the sensitivity of wave growth when relaxing the assumptions of strict Proudman resonance. Specifically, this study will focus on oceanographic factors (tides and sloping bathymetry) and atmospheric factors (varying forcing speed, varying pressure-forcing amplitude and two-dimensionality of atmospheric pressure forcings). This study presents more general dynamic explanations of wave growth by assuming that forced-wave and free-wave speeds are close and that wave flux is conserved. These dynamic explanations are found by using idealised analytical and numerical models, with mathematically prescribed pressure disturbances that are termed synthetic atmospheric forcings for consistency with the literature (e.g. Ličer et al. 2017).

This work is presented as follows. Section 2 describes the three different models that will be used in this study and the synthetic atmospheric pressure forcing that will be applied. Section 3 presents a baseline simulation of strict Proudman resonance. Section 4 tests the effect of oceanographic factors on this wave amplification, and, similarly, Sect. 5 tests the effect of atmospheric factors. Section 6 summarises these results.

2 Methods

To investigate the effect on wave growth from oceanographic and atmospheric factors, three oceanographic modelling methods (2D finite element, 2D finite difference and 1D finite difference) were used to solve the shallow-water equations. We call these models 2D-FE, 2D-FD and 1D-FD, respectively.

2.1 Hydrodynamic models

For the hydrodynamic models studied here, the non-advecting, frictionless, non-rotating, hydrostatic momentum equation and the continuity equation were solved, given as

$$ u_{t} = - \rho^{{{-}1}} P_{x} - g\eta_{x} , $$

(4)

$$ v_{t} = - \rho^{{{-}1}} P_{y} - g\eta_{y} , $$

(5)

and

$$ - \eta_{t} = \left[ {\left( {H + \eta } \right)u} \right]_{x} + \left[ {\left( {H + \eta } \right)v} \right]_{y} , $$

(6)

where u is the along-propagation current, v is the cross-propagation current and y is the cross-propagation direction. Equations 4–6 are solved in the domain 0 ≤ x ≤ L, 0 ≤ y ≤ W, with radiating boundary conditions at x = 0 and x = L and reflecting boundary conditions at y = 0 and y = W.

The finite-element model Telemac (Hervouet 2000) was used and has been validated for tsunamis and tides (called 2D-FE). For reduced computation time, and to allow multiple rapid simulations, a finite-difference method was also developed in one and two dimensions (called 1D-FD and 2D-FD, respectively). The finite-difference method (2D-FD and 1D-FD) is outlined in supplementary material, which does not include the sea-level elevation term in Eq. 6. This approximation is justified because sea-level elevation was very small compared to water depth (< 1%). Likewise, the differences between 2D-FE, 2D-FD and 1D-FD numerical solutions remained small with sufficiently small grid spacings and time steps. Each model was chosen by balancing computational expedience (e.g. runtime of each model), model simplicity (e.g. solving governing equations with appropriate dimensions) and model capabilities (e.g. time-varying boundaries).

2.2 Synthetic atmospheric forcing

The hydrodynamic model was forced with a synthetic atmospheric pressure field prescribed as two orthogonal cosines (Fig. 1, Eq. 7). This synthetic atmospheric pressure forcing P can be summarised as

$$ P = \left\{ {\begin{array}{*{20}l} {P_{0} \cos \psi \cos \gamma + P_{b} ,} \hfill & {{\text{if}}\; - N\pi \le \psi \le N\pi , y_{0} - \frac{{\lambda_{y} }}{4} \le \gamma \le y_{0} + \frac{{\lambda_{y} }}{4}} \hfill \\ {P_{b} ,} \hfill & {{\text{otherwise}}.} \hfill \\ \end{array} } \right. $$

(7)

Fig. 1

Synthetic atmospheric pressure in the domain 0 ≤ x ≤ L, 0 ≤ y ≤ W at different values of λ_y. Here, the pressure field is shown between −P₀ and +P₀, N = 1.5 and λ_y varied between a m > 0 and b m = 0. Panel a shows the cross-propagation wavelength (λ_y) compared to the total forcing width (W_F = λ_y/2) and along-propagation wavelength (λ_x) compared to the total forcing length (Nλ_x) of the pressure disturbances, with the definition of the aspect ratio A_P = λ_y/λ_x

The cosine arguments prescribed the two-dimensional pressure-forcing position and extent (Eq. 7). The first argument ψ prescribed the along-propagation speed and wavelength of the atmospheric forcing, ψ = kx − ωt. The along-propagation wavenumber was k = 2π/λ_x, where λ_x is the along-propagation wavelength (40 km), and the angular frequency was ω = 2π/τ, where τ is the wave period (28–37 min). The speed of the atmospheric forcing U was ω/k. The bounds of the argument, ± Nπ, ensured that N wavelengths were simulated. Here, N = 1.5 to imitate linear convective systems (e.g. Williams et al. 2019) or a section of an atmospheric gravity wave (e.g. Ličer et al. 2017).

The second argument γ prescribed the cross-propagation forcing extent, explicitly γ = m(y − y₀). The cross-propagation wavenumber was m = 2π/λ_y, where λ_y is the cross-propagation wavelength and y₀ = W/2. The argument bounds ensured that half of the cross-propagation wavelength was prescribed as the forcing width, W_F = λ_y/2 (Fig. 1a). For planar pressure forcings, we set m = 0 (Fig. 1b).

Finally, P₀ prescribed the maximum amplitude of the pressure-forcing disturbance, and the pressure perturbation was added to a background pressure, P_b = 1013 Pa. The parameters chosen here represented observed values for meteotsunami-generating convective systems (e.g. Anderson et al. 2015) and atmospheric gravity waves (e.g. Ličer et al. 2017).

Next, the model simulation results and discussion are divided into three sections: strict Proudman resonance, oceanographic factors and atmospheric factors. First, strict Proudman resonance is simulated in Sect. 3 to give baseline simulations. Second, the effect of oceanographic factors on wave amplification is tested in Sect. 4. This section quantifies the effect of tides and sloping bathymetry on wave amplification through a hierarchy of simulations. This hierarchy progresses from simulating the effects on wave amplification of separate uniform elevations (4.1) and uniform currents (4.2). Then, a combination of uniform elevations and currents are modelled together (4.3). After these simulations, the effect of variable free-wave speed through bathymetric slopes is found (4.4). Finally, in the hierarchy, spatially and temporally co-varying elevations and currents are simulated together (4.5). After oceanographic factors are tested, the effect of atmospheric factors on wave amplification is tested in Sect. 5. These simulations quantify the effect on wave amplitude by varying the average forcing speed (5.1), allowing the forcing speed to vary in time (5.2) and then forcing amplitude to vary in time (5.3), and finally, including the two-dimensionality of forcings (5.4).

3 Strict Proudman resonance simulation results and discussion

First, the strict Proudman resonance simulation is presented, to provide baseline results for the following simulations and to demonstrate consistency with previous simulations from Vilibić (2008). Only the 1D-FD results are presented (Fig. 2), although two-dimensional solutions were made equivalent to one-dimensional solutions by setting reflecting boundary conditions at y = 0 and y = W. All three models were run with λ_x = 40 km, P₀ = 100 Pa, in a H = 50 m, L = 400 km domain. The atmospheric forcing moved 10 wavelengths, corresponding to the distance scales (100 s km) and the timescales (several hours) of mesoscale atmospheric systems that produce waves through Proudman resonance (Monserrat et al. 2006). The atmospheric forcing was also smoothed with a 5-km running average to ensure that the atmospheric-forcing edges gradually returned to background pressure, rather than an unphysical, sharp cut-off.

Fig. 2

Flat-bottom strict Proudman resonance simulation results at four time steps (t₀, t₁, t₂, t₃) for a rightward moving pressure forcing. The x-axis shows the number of wavelengths travelled. The vertical grey dashed lines indicate pressure-forcing extent at each time step. a Normalised pressure disturbance, b amplification (the normalised sea-level response). The red dashed lines show the wave envelope analytic solution for a sinusoidal pressure disturbance, and the blue dashed lines show the same for a piecewise linear pressure disturbance with the same peak amplitude. Normalised pressure disturbances and amplifications magnitudes < 0.001 are not shown

The 1D-FD pressure forcing and resulting sea-level elevation were made dimensionless. The sea-level elevation η was divided by P₀/ρg, giving the dimensionless amplification, η*, and the distance travelled was divided by wavelength λ_x, giving dimensionless wavelengths travelled, x* (Fig. 2).

There are three main features of the one-dimensional solution. First, the wave shape was that of the atmospheric pressure disturbance gradient multiplied by negative 1. The wave shape is explained by the wave shape from free-wave and forced-wave superposition as Fr → 1.

Second, the wave amplification increased linearly for every wavelength moved (Fig. 2b). The maximum wave amplification of this simulation is shown in Table 1. Table 1 is the synthesis of all simulations, showing the simulation number (e.g. 0), model type (e.g. 1D-FD), feature changed within a factor (not applicable here, but an example is tidal elevation), test simulation (e.g. baseline or + 4 m), maximum recorded amplification (e.g. 31.1) and location of maximum recorded amplification (e.g. 9.9). The strict Proudman resonance simulation has simulation number 0 to indicate that it is the baseline model. This simulation has a maximum recorded amplification of 31.1 and location of maximum recorded amplification of 9.9, and the wave grew 3.1454-fold (3.1454 ≈ π + 0.12%) for every wavelength moved. Likewise, in the 2D-FD model the wave grew 3.1265-fold (π − 0.48%) and in the 2D-FE model the wave grew 3.1607-fold (π + 0.61%) for each wavelength moved (see Supplementary Material).

Table 1 Simulation number, model, feature changed, test simulation, maximum recorded amplification and location of maximum recorded amplification across 50 simulations

The maximum modelled amplification and wave growth are understood through the analytic solution of the maxima and minima of amplification. By inputting an infinite and planar sinusoidal pressure forcing into Eq. 3 and taking the solution maxima, the amplification envelope $\eta_{\text{env}}^{*}$ is

$$ \eta_{\text{env}}^{*} = \pm \pi x^{*} , $$

(8)

showing that a wave produced from a resonant sinusoidal pressure forcing will amplify π-fold for every wavelength moved. The numerical model overpredicted analytical growth by 0.12%, partly because of small numerical errors that could not be avoided. The forcing was not precisely specified as a sinusoid that smoothly moved with time, but as a discretised series of points on a line that approximated a sinusoid, and this forcing discretely (rather than smoothly) moved at specific time steps. Despite small discrepancies between numerical and analytical solutions, under strict Proudman resonance, an atmospheric forcing will produce an envelope according to

$$ \eta_{\text{env}}^{*} = \pm \mu x^{*} , $$

(9)

where μ is the growth factor, which is the gradient of the envelope and is dependent on the pressure-forcing shape. A growth factor μ = 2 is well known for a piecewise linear forcing (Hibiya and Kajiura 1982; Vilibić 2008).

Third, simulations showed a smaller leading trough and smaller trailing peak (respectively, LT and TP in Fig. 2b). The leading trough and trailing peak occurred because of the shape of the pressure forcing, but their magnitudes were smaller than $\pi x^{*}$ because the forcing was smoothed at its edges.

4 Oceanographic factors: results and discussion

Once the model had been validated through strict Proudman resonance stimulations, the effect of oceanographic factors on wave growth was quantified. A hierarchy of simulations was used to quantify the effect of tides and sloping bathymetry on Proudman resonant wave growth.

4.1 Uniform elevation change (1D-FD)

First, uniform elevation changes were modelled. To model the effect of tides, and because most tidal ranges are less than 8 m, water depths were changed between − 4 m and + 4 m. For a typically fast-moving atmospheric forcing that generates meteotsunamis, this tidal range was represented here by elevation changing from a baseline depth H₀ of 50 m by a uniform change ΔH.

When changing the water depth (simulations 1–4), the maximum wave amplification was smaller than from strict Proudman resonance. For example, when ΔH = − 2 m (simulation 2) wave amplification was 6.4% smaller than strict Proudman resonance and when ΔH = + 2 m (simulation 3), the maximum wave amplification was 3.8% smaller than strict Proudman resonance. Comparing ΔH = − 2 m (simulation 2) with ΔH = + 2 m (simulation 3) and ΔH = − 4 m (simulation 1) with ΔH = + 4 m (simulation 4), waves were slightly larger when elevation increased than for an equivalent elevation decrease.

These maximum wave amplifications are the maxima of the wave amplification envelopes (see relationship in Fig. 3a, b). These wave amplification envelopes are now explained through changes to shallow-water wave speed affecting Proudman resonance. For similarity with the literature, we define ‘near-Proudman resonance’ to occur when 0.9 ≤ Fr ≤ 1.1 or, equivalently, when the free-wave speed and forced-wave speed are within 10% of each other (e.g. Vilibić 2008; Šepić et al. 2015). In these simulations, the approximate shallow-water wave speed is given by Eq. 1 with water depth H(x) = H₀ + ΔH and u_c = 0. When the atmospheric forcing is near the shallow-water wave speed (i.e. near-Proudman resonance), and assuming an infinite, planar sinusoidal pressure forcing in Eq. 2, the sea-level amplification η* can be approximated as

$$ \eta *(x, t; k, U, c) \approx 2 \bar{A}\left( {\text{Fr}} \right) \cdot \sin \left[ {k\frac{U - c}{U + c}x} \right] \cdot \cos \left[ {k\left( {x - \frac{U + c}{2}t} \right)} \right] = E\left( x \right)W(x - \bar{U}t), $$

(10)

which describes the sea-level elevation as a wave propagating at the mean speed, $\bar{U}$, of the forced and free wave (cosine term). This propagating wave is modulated by a sinusoid with an envelope wavenumber given as the atmospheric-forcing wavenumber k multiplied by a Doppler shift (U − c)/(U + c). The wave amplitude is then multiplied by the mean Proudman resonant amplitude $\bar{A}\left( {\text{Fr}} \right)$, which is the mean of the coefficients of the rightward forced and free waves in Eq. 2. The factor of 2 arises from using the trigonometric identity in the approximation. This approximation, which is only valid when the forced wave and free wave are close, is summarised as the envelope $E(x)$ multiplied by a wave $W(x - \bar{U}t)$. When the forced wave and free wave are far, the amplitude of the waves is given in Eq. 2. Equation 10 has been adapted from Ličer et al. (2017) to include wave amplitude and to make the envelope wavenumber more explicit. Equation 10 is originally used to explain meteotsunami propagation speed, but we use it to explain the envelopes.

Fig. 3

Flat-bottom 1D-FD model results at four time steps (t₀, t₁, t₂, t₃) for a rightward moving pressure forcing at U = 22.15 ms⁻¹ at different elevation changes (ΔH) where a ΔH = − 4 m (simulation 1), b ΔH = + 4 m (simulation 4). The x-axis is the dimensionless wavelength travelled, and the y-axis is the dimensionless amplification. The dashed blue lines show the analytical solution to the wave envelope for a sinusoidal pressure disturbance at resonance, and the dashed red lines show the wave envelope approximations. c Analytical envelope approximations with uniform elevation changes that closely matched maximum amplification from 1D-FD simulations. Dashed black lines are elevation decreases and solid black lines are elevation increases

Envelopes matched the maximum wave amplification within 4.3% across simulations 1–4. Waves were larger when elevation was increased because the change in shallow-water wave speed was smaller when increasing elevation, leading to closer approximations of Proudman resonance. Therefore, these models suggest that it is slightly more important to account for elevation decreases (e.g. low tide) than elevation increases (e.g. high tide) because wave growth deviates more from strict Proudman resonance with elevation decreases than with elevation increases.

Summarising these results, when Proudman resonance was more closely approximated, larger waves were generated. Although simulations 1–4 only covered four combinations, a more general form for the amplification envelope has been developed (Eq. 10) that can be used to describe any combination of atmospheric-forcing speed and water depth change (Fig. 3c). Again, this general amplification envelope is only valid whilst the forced wave and free wave are close. Instead of the wave amplification reducing to 0, as it would seem in the case of 20 m and 80 m water depths, the waves separate with individual wave heights as predicted by Eq. 2. This more general amplification envelope is used later to help explain the effect of other oceanographic assumptions and is appropriately adjusted to include other physical phenomena, for example wave-flux conservation with currents.

4.2 Uniform current (2D-FE)

Once the wave amplification with uniform elevation changes was simulated and explained, uniform currents were modelled. Strict Proudman resonance requires a still ocean, so the suite of simulations in this section allows us to explore the sensitivity of the wave growth to a uniform ocean current. In our simulations 5–12 (Table 1), the model initial conditions and boundary conditions were the along-propagation tidal current speed u_c. The current effects were isolated by excluding friction, meaning that background water depth remained constant. We simulated − 3.0 ms⁻¹ ≤ u_c ≤ + 3.0 ms⁻¹, where positive currents were rightward.

The maximum wave amplitudes were consistently larger as the magnitude of u_c decreased. The maximum wave amplitude was on average 3.8 times larger with 0.5 ms⁻¹ than 3 ms⁻¹ magnitude currents (cf. simulations 8 and 9 with simulations 5 and 12). Wave growth was also different for currents of the same magnitude moving in different directions. When |u_c| = 3 ms⁻¹, the maximum amplification was 4% smaller and occurred 1.1 wavelengths leftwards with counter-currents (simulation 5) compared to along-propagation currents (simulation 12). Similarly, when |u_c| = 2 ms⁻¹, maximum amplification occurred 0.7 wavelengths leftwards with counter-currents (simulation 6) than along-propagation currents (simulation 11), but the maximum amplifications were of similar magnitude. Conversely, when currents were smaller (|u_c| = 0.5 and |u_c| = 1 ms⁻¹), maximum wave amplifications were on average 8% larger with counter-currents (simulations 7–8) compared to along-propagation currents (simulations 9–10). Therefore, smaller currents always produced larger waves, but maximum wave amplification was different for opposite currents of the same magnitude by a few per cent.

The resultant wave amplification for all constant currents can be explained by a near-Proudman resonant envelope approximation (Eq. 10) combined with wave-flux conservation. A small-amplitude wave (as studied here) entering a region with a current will change wave height to conserve wave energy flux according to

$$ \frac{{\eta_{c} }}{{\eta_{0} }} = \frac{1}{{(1 + f_{c} )}}, $$

(11)

where the subscript ‘c’ refers to the variable with a current and subscript ‘0’ refers to the variable without a current. The dimensionless current factor f_c refers to the ratio of current speed to shallow-water wave speed ($u_{c} /\sqrt {gH}$). A current in the same direction as a wave (along-propagation current) will decrease the wave height, and a counter-current will increase the wave height. Finally, wavelength also changes with currents according to

$$ \frac{{\lambda_{c} }}{{\lambda_{0} }} = 1 + f_{\text{c}} , $$

(12)

showing that along-propagation currents increase wavelengths and counter-currents decrease wavelengths (Li and Herbich 1982; Choi et al. 2014).

An additional simulation was performed with an atmospheric-forcing speed U = 15 ms⁻¹ (Fr = 0.68) to confirm the effect of currents on forced waves and free waves (not in Table 1 because the purpose of this simulation is separate to the focus of main study results). Over 4.4 h (16,000 s) of simulation time, forced waves and free waves separated, and the effect of currents was seen on both waves. When currents were included, both the forced-wave and free-wave heights changed according to Eq. 11. The free-wave wavelength also changed according to Eq. 12. However, the forced-wave wavelength did not change, because it was fixed by the forcing wavelength. Therefore, both waves were amplified by currents, but only the free wave changed wavelength.

This information was then used to approximate the envelope wavelength and magnitude with currents (Fig. 4, Supplementary Figure S1). The envelope wavelength was calculated with the average of forced-wave and free-wave wavelengths, and the envelope magnitude was multiplied by the right-hand side of Eq. 11. This envelope approximated maximum wave amplification within 5.2%. The envelopes were different for positive and negative currents for two reasons—wave amplification (Froude number and wave-flux conservation) and free-wave wavelength modification (wave-flux conservation).

Fig. 4

Analytical envelopes with uniform currents that closely matched maximum wave amplification from 2D-FE simulations. Dashed black lines are counter-current, and solid black lines are along-propagation currents

Wave envelopes have so far been described for elevation-only changes (simulations 1–4) and current-only changes (simulations 5–12). In the real world, these simulations may represent how standing-wave tides at different tidal states (e.g. high tide, flooding tide) may affect wave growth. For standing-wave tides, when the tidal elevation is 0 m, the current is flooding (maximum positive current) or ebbing (maximum negative currents). Conversely, slack tide (u_c = 0 ms⁻¹) occurs at high tide and low tide. These envelopes may be used to predict how much tidal elevations and currents individually affect wave growth.

4.3 Uniform elevation and current (2D-FE)

In the real ocean, elevation changes and currents may not be separated. Therefore, uniform elevation and currents were modelled together in simulations 13–20 (Table 1). As before, the bottom elevation was changed from H₀ = 50 m by ΔH, where ΔH was − 4 m, − 2 m, + 2 m and + 4 m. This elevation was combined with a constant current of either − 1 ms⁻¹ or + 1 ms⁻¹.

The resultant waves were dependent on combined elevation and currents. With counter-currents (simulations 13–16), as elevation increased from − 4 to + 4 m, the maximum wave amplifications increased by 174% and moved 3.9 wavelengths rightward. With along-propagation currents (simulations 17–20), as the elevation decreased from + 4 to − 4 m, the maximum wave amplifications increased by 128% and moved 3.4 wavelengths rightward. Each combination of elevation and current produced unique wave amplification envelopes.

The envelope approximations used the combination of both the elevation effect on Proudman resonance and current effect on Proudman resonance and wave-flux conservation (Fig. 5, Supplementary Figure S2). Accounting for both elevation and currents, envelopes approximated maximum wave amplifications to within 4.4%.

Fig. 5

Analytical envelopes with uniform elevation and currents that closely matched maximum wave amplification from 2D-FE simulations. Dashed black lines are counter-currents, solid black lines are along-propagation currents, and elevation changes are annotated

Most combined current and elevation simulations 13–20 produced sub-Proudman resonant wave amplification. However, the wave growth with u_c = − 1 ms⁻¹ and ΔH = + 4 m (simulation 16) produced growth that was 3% larger than Proudman resonance predictions, termed super-resonant wave growth.

This super-resonant growth occurred because the wave speed changes from elevation were compensated by counter-currents and because of wave-flux conservation. This super-resonant growth is not confined to elevation and current changes together. It may also occur with an atmospheric forcing that is moving slower than the depth-dependent wave speed against a counter-current such that the Froude number is near 1.

In the real world, simulations 13–20 may represent Proudman resonance in a progressive tide, with floods at high tide and ebbs at low tide. In progressive tides, currents and tidal elevation are in phase, meaning that, across a tidal cycle, shallow-water wave speed may be more variable than in standing-wave tides. Therefore, meteotsunami generation within progressive-wave tides may be more controlled by tidal state (e.g. high tide, falling tide) than generation within standing-wave tides.

4.4 Bathymetric slope (2D-FE)

Next, we varied the bathymetric slopes. Strict Proudman resonance requires a flat-bottomed ocean, so the suite of simulations 21–24 in this section allows us to explore the sensitivity of wave growth to the magnitude and sign of a bathymetric slope (upward or downward). Previous studies have numerically modelled Proudman resonance with sloping bathymetry (e.g. Vilibić 2008; Ličer et al. 2017; Choi and Seo 2017; Chen and Niu 2018). However, we explicitly design our models to isolate the effect of a linear slope even with an average Froude number of 1, which others have not done.

To understand how a slope may affect wave growth, we refer to the interaction between forced waves and free waves generated by a forcing. Recall from the derivation of Eq. 3, as Fr → 1, the physical separation between the forced wave and free wave decreases and Proudman resonance occurs. However, across variable bathymetry, individual free waves are continuously generated, which combine to form a free-wave superposition (Ličer et al. 2017). Therefore, the separation is dependent on the positions of the forced wave and the free-wave superposition. The position of the forced wave leading edge x_U is given by the forcing speed U multiplied by time t. However, the position of the free-wave superposition is more complex than the forced-wave position because multiple free waves are generated.

To parameterise the position of the free-wave superposition, the leading edge position of the farthest free wave from the forced wave was calculated. This free-wave position x_c was calculated for a basin of length L with depths H(x = 0) = H₀ and H(x = L) = H₁. By first integrating the inverse free-wave speed c⁻¹(x) with respect to x, and then rearranging, we obtained

$$ x_{c} \left( t \right) = \frac{{g(H_{1} - H_{0} )}}{4L}t^{2} + \sqrt {gH_{0} } t, $$

(13)

showing that x_c is quadratic in time, which directly arises from the linearly sloping bottom. Then, the difference between x_U(t) and x_c(t) was calculated, given the separation Δx(t).

The slopes were then set such that Δx = 0 at the start and end of propagation. In other words, the average free-wave speed was made equal to the average forced-wave speed to isolate the slope effect. Four simulations were completed: simulation 21) H₀ = 30 m, H₁ = 75.1 m (steep downslope); simulation 22) H₀ = 40 m, H₁ = 61.1 m (shallow downslope); simulation 23) H₀ = 60 m, H₁ = 40.9 m (shallow upslope); and simulation 24) H₀ = 70 m, H₁ = 33.4 m (steep upslope). These slopes were similar magnitude to realistic bathymetry in shallow shelves, seas and lakes (0.05–0.1 m km⁻¹, Supplementary Figure S3).

With all slopes, the maximum wave amplification was lower than from strict Proudman resonance (cf. simulation 0 with simulations 21–24, Fig. 6). However, maximum wave amplifications were 32% larger with shallow slopes (simulations 22–23) than steep slopes (simulations 21 and 24) and 17% larger with upward slopes (simulations 23–24) than downward slopes (simulations 21–22). These results are illustrated by the smallest wave being generated with the steep downslope (simulation 21) and the largest wave with the shallow upslope (simulation 23).

Fig. 6

Sloping bottom maximum wave amplifications from 2D-FE simulations. Black solid lines are effective Froude number envelopes. Grey dots are simulation maxima for downward slopes, and white dots are simulation maxima for upward slopes. Maxima are joined by grey lines (linear interpolation). Simulation envelopes and envelope approximations are annotated with simulation numbers 21–24

In each sloping bathymetry simulation, but most notably in the steep downslope, the wave envelope amplification was smaller and modulated along the wave propagation direction (Fig. 6). For all other slopes, there was a qualitatively similar, though smaller, envelope modulation. These envelope modulations were related to the magnitude of Δx in time.

We suggest that the wave envelopes may be better approximated by accounting for Δx(t), rather than simply using the average free-wave speed (c = 22.15 ms⁻¹). Nonetheless, directly accounting for Δx(t) is complicated. A simpler way to include the separation effect is to account for the maximum separation:

$$ \Delta x_{\hbox{max} } = \frac{{c_{0} - U}}{4}T. $$

(14)

Equation 14 shows that the maximum separation was directly proportional to both the difference in free-wave and forced-wave speeds and the time taken to cross the basin. The separation was positive for upward slopes and negative for downward slopes.

To account for Δx_max, we introduced a constant, effective free-wave speed c_eff. This effective free-wave speed gave the same maximum separation over the propagation time T of the free wave and forced wave and was calculated as

$$ c_{\text{eff}} = \bar{c} + \frac{{\Delta x_{\hbox{max} } }}{T}, $$

(15)

where $\bar{c}$ is the mean free-wave speed (22.15 ms⁻¹). The effective Froude number, here Fr_eff = U/c_eff, shows that effective Froude number was within ranges of near-Proudman resonance. For example, the effective Froude number was 0.96 for the steep upward slope, compared to an instantaneous Froude number between 0.82 and 1.18. The envelope from an effective Proudman resonance was calculated with Fr_eff in Eq. 10. Fr_eff was nearer 1 for shallower slopes and upward slopes, which may explain why waves were larger for shallow slopes than steep slopes and larger for upward slopes than downward slopes.

The wave heights may also have been larger for upward slopes than downward slopes because of wave-flux conservation. Thus, the wave height increase from shoaling was also accounted for according to Green’s law:

$$ \frac{\eta \left( x \right)}{{\eta_{0} }} = \left[ {\frac{H\left( x \right)}{{H_{0} }}} \right]^{ - 1/4} . $$

(16)

This shoaling contributed to wave height for upward slopes and reduced wave height for downward slopes. The free-wave wavelength also decreased with decreasing depth. Thus, average wavelength changes were included, but their effect seemed negligible.

Our results and explanation complement previous studies of sloping bottoms. It is well known that envelopes along sloping bottoms are complex (e.g. Vilibić 2008; Chen and Niu 2018) and that wave envelopes are larger with shallow slopes than steep slopes (Chen and Niu 2018). However, we show that it may prove useful to consider Δx and Fr_eff to help explain wave growth along sloping bottoms, rather than considering the instantaneous Froude number at several points along a slope (e.g. Choi and Seo 2017; Chen and Niu 2018). The envelopes with effective wave speed and shoaling produced better approximations of wave growth than strict Proudman resonance by parameterising the effect of variable free-wave speeds (Fig. 6). However, the envelopes derived from the effective wave speeds were still not useful indicators of instantaneous wave height. Discussion of the effective Froude number continues in Sect. 5.2.

4.5 M₂ progressive tides (2D-FE)

Finally, in the hierarchy, co-varying depths and currents were modelled with an M₂ tide approximation in simulations 25–28. The M₂ constituent was chosen because it is normally the largest tidal constituent in basins (e.g. Pugh and Woodworth 2014). The model was spun-up over 6 days with a boundary condition at x = 0, prescribing a 12.4-h period sinusoid with 4-m amplitude. For model stability with a time-variable boundary condition, a constant horizontal diffusivity was included (150 m²s⁻¹). An additional simulation without tides and with diffusivity showed that diffusivity reduced maximum wave amplification by < 1%.

Once the tidal simulation was spun-up and stable, the tidal-wave speeds were approximated. Here, the tidal-wave speed was the speed at which the relevant phase of the sinusoid moved across the domain. At four tidal states, the tidal-wave speeds were estimated within one standard deviation. These speed estimates were 20.1 ± 0.6 ms⁻¹ at low tide, 20.5 ± 1.3 ms⁻¹ at rising tide, 23.4 ± 0.9 ms⁻¹ at high tide and 21.7 ± 0.6 ms⁻¹ at falling tide. The tidal-wave speed varied between tidal states primarily because tidal amplitude was about 8% of the total water depth.

The water depths and currents were similar to those previously modelled in Sects. 4.1–4.4. The maximum water level varied between 46 and 54 m, and the current co-varied between − 1.8 and + 1.7 ms⁻¹, within the ranges examined in Sects. 4.1–4.3. During falling and rising tide, the current was between about − 0.5 and + 0.5 ms⁻¹ and the water depth was between about 49 m and 51 m across the full atmospheric-forcing length (Nλ_x) (Fig. 7a), meaning that free-wave speed varied across the forcing length similarly to examined in Sect. 4.4. Therefore, the analyses developed in previous sections were applied to these M₂ tidal simulations.

Fig. 7

Sea-level elevation and amplification from a moving forcing with a dynamic progressive tide with 2D-FE simulations. a Sea-level elevation directly from the falling tide simulation at four time steps (t₀, t₁, t₂, t₃) and b band-passed filtered sea-level elevation converted to amplification. Blue dash-dots are initial estimates of c_p,T (21.7 m s⁻¹) and u_c,T (0 m s⁻¹), and the red solid line is the envelope with improved c_p,T and u_c,T. Black dots are maxima and minima of sea-level amplification at 500-s intervals between 4500 and 15,000 s. Amplification values more than 0.5λ_x ahead of and behind the forcing have been cropped for clarity. c Black dashed lines are the envelope approximations with the lowest error of the maxima recorded amplitude. The grey dots are simulation maxima, joined by grey lines (linear interpolation)

For each simulation, an atmospheric pressure forcing was applied, moving rightward at speed U = 22.15 ms⁻¹. The centre of the atmospheric pressure perturbation (P = P_b + 100 Pa) first coincided with each tidal state at x = 0, but the atmospheric forcing’s tide-relative position slightly drifted along propagation. This drift was because the atmospheric-forcing speed differed from tidal-wave speed. The resulting sea-level elevation from the atmospheric forcing moving over falling tide is shown in Fig. 7a.

To analyse the wave amplification separately from tidal elevation, a fourth-order 2–100 km bandpass Butterworth filter was applied to the sea-level elevation [implemented as the digitised ‘butter’ function from SciPy, which was adopted from Butterworth (1930)]. The wave growth at falling tide was 10% larger than strict Proudman resonant growth and thus super-resonant (Fig. 7b). All other simulations produced near-resonant wave growth (Fig. 7c, Supplementary Figure S4). The maximum wave amplification was also 23% larger at high tide than low tide, and 5.4% larger at falling tide than rising tide. These resultant amplifications are similar to the results from tidal elevation and tidal current simulations in Sect. 4.3.

As the tide is a shallow-water wave, the free-wave speeds were approximated by the tidal-wave speed c_p,T and currents were approximated by the tidal currents at the centre of the wave u_c,T. Single values of the c_p,T and u_c,T were applied in the same way as with sloping bottoms (Sect. 4.4), but errors associated with this simplification were accounted for in the estimations.

The largest errors in the stationary and the wave’s reference frames were accounted for when estimating the tidal-wave speed and current. The stationary reference frame error was from tidal-wave speed approximations (stated within one standard deviation). Two more errors from the wave’s reference frame were also estimated. The first error was from the atmospheric-forcing drifting relative to tidal state, and the second error was from changes in water depth and currents across the full atmospheric-forcing length. The estimates of c_p,T and u_c,T that produced wave envelope approximations that were closest to numerical solutions are shown in Fig. 7c. These simulations reiterated the results from previous simulations 1–24; wave growth may be closely approximated in dynamic tidal regimes by accounting for Proudman resonance and wave-flux conservation using single, representative values of free-wave speed and currents.

So far, we have explained wave growth with changes to uniform water depth (simulations 1–4), uniform currents (simulations 5–12), uniform elevation and currents (simulations 13–20), bathymetric slope (simulations 21–24) and progressive M₂ tides (simulations 25–28). At least for the water depths considered here, when examined individually, currents were more important than elevations within typical tidal ranges. However, elevation changes and currents should be considered together to properly understand the resultant nonlinear changes to maximum wave amplification. Understanding the combination of elevations and currents allowed close approximations of maximum wave growths from progressive tidal simulations. Overall understanding was supplemented by bathymetric slope simulations, which showed that near-Proudman resonant wave growth could occur even when the instantaneous Froude number varied between 0.82 and 1.18, because the effective Froude number was near 1.

5 Atmospheric factors: results and discussion

Next, the atmospheric-forcing assumptions of constant speed, constant amplitude and one-dimensionality were investigated for flat bathymetry without elevation changes or currents.

5.1 Average forcing speed (1D-FD)

Common methods to estimate atmospheric-forcing speed use land-based in situ high-frequency measurements (Orlić 1980; Vilibić et al. 2008; Choi et al. 2014), radar reflectivity (Wertman et al. 2014; Williams et al. 2019) or numerical weather prediction models (Horvath and Vilibić 2014; Anderson et al. 2015). However, it is sometimes difficult to calculate atmospheric-forcing speed within 10% accuracy (Wertman et al. 2014), leading to uncertainty in the maximum wave growth due to Proudman resonance. This uncertainty can occur even with high-fidelity bathymetry and accurate tidal modelling (Williams et al. 2019). To account for uncertainty in average atmospheric-forcing velocity, multiple simulations with different velocities may be required (e.g. Ličer et al. 2017).

To test the wave growth from different atmospheric-forcing speeds, the baseline speed U₀ = 22.15 ms⁻¹ was changed by − 2 ms⁻¹ ≤ ΔU ≤ + 2 ms⁻¹ (simulations 29–32). These simulations were modelled with H = 50 m, λ_x = 40 km and N = 1.5. The resultant wave amplification for constant atmospheric-forcing speeds produced near-Proudman resonance wave growth, giving results that were explained using the same envelope as for water depth changes (Eq. 10), which were accurate within 0.9% (Supplementary Figure S5).

Reasonable uncertainties in the average speed of a fast-moving atmospheric forcing (± 10%, simulations 29–31) produced larger changes in sea-level elevation than reasonable uncertainties due to large tidal elevation (|ΔH| = 4 m, simulations 1 and 4) and weak currents (|u_c| < 1 ms⁻¹, simulations 7–10) alone. The wave growth from changing atmospheric-forcing speeds was similar to large tidal elevation with currents (ΔH = − 4 m, u_c = + 1 ms⁻¹, simulation 17), strong currents alone (|u_c| > 1 ms⁻¹, simulations 5, 6, 11 and 12), steep downward slopes (simulation 21), M₂ low tide (simulation 25) and M₂ high tide (simulation 28).

Therefore, obtaining accurate estimates of average forcing velocity is as important as quantifying the combined effect of tidal elevation and currents. We speculate that, for the purposes of meteotsunami generation, a calculated forcing velocity is more accurate when obtained from measurements over water (e.g. radar) than from measurements over land (e.g. in situ land stations). A lower velocity may be calculated over land, because land is more heterogeneous and has a higher coefficient of friction than the ocean. Therefore, for the purpose of inferring Proudman resonance or using velocity calculations in synthetic models, when it is possible, atmospheric-forcing velocities should be obtained through measurements of the atmospheric system over water.

5.2 Variable forcing speed (1D-FD)

The motion of mesoscale atmospheric systems that generate meteotsunamis, such as convective systems, can be highly variable due to internal processes within the mesoscale systems and external environmental conditions. For example, there is discrete propagation from gust fronts, interactions between convective and stratiform components of storms, and how the storm evolves within the larger-scale environmental conditions such as wind shear or rear inflows (Markowski and Richardson 2011 pp. 245–265) (for which we assume the pressure field is related to the precipitation field observed by radar). However, strict Proudman resonance assumes a constant motion of the forcing. Even for convective systems that form meteotsunamis, the system velocity can be highly variable over time (Wertman et al. 2014) and differ across scales within a convective system (Williams et al. 2019). Thus, we quantify the effect of variable atmospheric-forcing speeds on wave amplification in simulations 33–40.

First, the sensitivity of wave growth with linear forcing speed changes was investigated (simulations 33–36, Supplementary Figure S6). When the forcing speed changed linearly (i.e. constant acceleration), resultant wave growth was qualitatively similar to sloping bottoms (Sect. 4.4). Effective Froude numbers for variable forcing speeds were quantitatively the same as for linearly sloping bathymetry (Eq. 15); the effective Froude number can be used for either free waves or forced waves with variable speed.

Next, a sinusoidal pressure-forcing speed was applied such that the average speed was 22.15 ms⁻¹, the speed at the start and end of the movement was 22.15 ms⁻¹ and the difference between the highest and lowest forcing speed was the speed change ΔU. A weak speed change of 4 ms⁻¹ and a strong speed change of 8 ms⁻¹ were modelled. Also, a slow speed modulation (number of cycles = N_u = 1) and a rapid speed modulation (N_u = 2) were modelled to investigate the effect of the frequency of speed oscillations.

Again, smaller changes in atmospheric-forcing speed meant that the wave growth was more closely approximated by linear growth (Fig. 8, Supplementary Figure S6). However, more rapidly changing atmospheric-forcing speeds also produced wave growth that was more closely approximated by linear growth. Interestingly, the maximum wave amplification from the weak, slow speed modulation was equivalent to the maximum wave amplification from strong, rapid speed modulation (cf. simulations 38 and 39 in Table 1 and Fig. 8).

Fig. 8

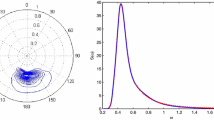
Maximum wave amplification with sinusoidally varying forcing speed, from 1D-FD simulations. Black solid lines are effective Froude number envelopes. Grey dots are simulation maxima for N_u = 1, and white dots are simulation maxima for N_u = 2. Maxima are joined by grey lines (linear interpolation). The values of ΔU/N_u are annotated in metres per second

To explain these results, the relationship between maximum separation, speed change and number of cycles was found. Analysis between forced and free waves with sinusoidally varying atmospheric-forcing speed gave a maximum separation:

$$ \Delta x_{{\text{max}}} = \frac{\Delta U}{{2\pi N_{u} }}T, $$

(17)

where Δx_max is positive for an atmospheric forcing that initially moved faster than the shallow-water wave speed. More rapidly varying atmospheric-forcing speeds (higher N_u) also had smaller maximum separations. Also, Eq. 17 shows that maximum separation was the same for the weak, slow modulation simulation 38 and the strong, rapid modulation simulation 39 because ΔU/N_u = 4 ms⁻¹ for both simulations.

The effect of Δx_max was then applied through the effective Froude number (Fr_eff) calculated with the effective forcing speed and free-wave speed. Fr_eff better approximated the growth of the wave than the average Froude number (Fig. 8). Across simulations 29–40 (except simulation 37), the average Froude number overpredicted maximum amplification by 17% on average, whereas Fr_eff overpredicted maximum amplification by 1.2% on average. Where Fr_eff overpredicted amplitude by 42% in simulation 37, the average Froude number performed even more poorly, overpredicting amplitude by 124%.

Even when the instantaneous Froude number strongly varied from 1 (e.g. simulation 36, 0.82–1.18), if the effective Froude number was near 1 (e.g. 0.96), then near-Proudman resonant wave growth could occur. The effective Froude number was nearer 1 when the mean atmospheric forcing and free-wave speeds were equal, when the variations around the mean forced or free speed were small and when those variations were rapid. Often studies have used instantaneous Froude numbers between 0.9 and 1.1 to indicate Proudman resonant regions (e.g. Šepić et al. 2015). Based on the results of our simulations, we suggest that this range may be increased to between 0.8 and 1.2.

The effective Froude number was not a useful quantity to give predictions of instantaneous amplification along propagation. The effective speed poorly approximated the instantaneous sea-level elevation in all simulations, especially at the maximum separation between forced waves and free waves (Figs. 6, 8). However, the effective Froude number may successfully parameterise the bulk effect of variable forced-wave or free-wave speeds on wave growth.

The usefulness of the effective Froude number may depend on the maximum separation of the waves compared to their wavelength. The maximum separation of the waves is dependent on the total forcing time (T), the rate of the speed change (N_u) and the maximum speed difference (ΔU). When using the effective Froude number to predict envelopes, smaller separations gave smaller errors. For example, when Δx_max = 0.58λ (simulation 37) there was a 42% overprediction and when Δx_max = − 0.45λ (simulation 33) there was a 6.4% underprediction. Further research may reveal under which conditions the effective Froude number is most useful. However, these results indicate that the effective Froude number is a more useful bulk parameter than the average Froude number to indicate Proudman resonant wave growth.

5.3 Time-varying amplitude of atmospheric forcing (1D-FD)

Mesoscale atmospheric processes will vary over the time that the wave is coupled to the forcing (a few hours), and these variations may increase or decrease atmospheric-forcing amplitude. For example, during the life cycle of a convective system, the system will initiate, grow, mature and decay (e.g. Johnson 2001).

Rather than first simulating the sea-level elevation and finding analytical approximations to numerical simulations to help explain the results, in this section, analytical solutions were directly found for variable amplitude forcings. This approach was taken because the analytical solution required only a simple generalisation of the forcing amplitude. Then, numerical simulations 41–43 were completed as supporting evidence (Supplementary Figure S7).

Here, analytical solutions were found for sea-level elevation from a variable amplitude forcing moving at Proudman resonant speed, for a one-dimensional, linear, frictionless, non-rotating ocean. A pressure forcing π was prescribed in a moving reference frame ξ = x − ct as a non-varying component P(ξ) multiplied by a time-varying component α(t) (− 1 ≤ α(t) ≤ 1).

The derivation of Proudman resonance under a constant-amplitude forcing from Churchill et al. (1995) was used as guidance, producing

$$ \eta (\xi , t) \approx - \frac{H}{2c\rho }P_{\xi } \int \alpha {\text{d}}t. $$

(18)

Under Proudman resonant speeds, the sea-level elevation in the moving reference frame is proportional to the time-integrated forcing amplitude. When α(t) = 1 (i.e. dα/dt = 0), Eq. 18 recovers linear wave growth according to strict Proudman resonance (Eq. 3). In the case that dα/dt ≠ 0, Eq. 18 suggests nonlinear wave growth under Proudman resonance. We show this relationship under the simple case of α(t) (1) linearly increasing (growth), (2) linearly decreasing (decay) and (3) as a half-wavelength sinusoid (growth from zero, maturation and decay back to zero).

The linearly changing amplitude forcings (0 ≤ α(t) ≤ 1) gave quadratic growth (Fig. 9a). For the linearly increasing forcing, the amplification quadratically increased at an increasing rate, and for the linearly decreasing forcing, the amplification quadratically increased at a decreasing rate. Simulations 41–42 reiterated these analytical solutions. Analytical solutions show that maximum amplification for both linear increase and linear decrease, η* = 5π at x* = 10, which is half of the maximum amplification from a constant-amplitude forcing.

Fig. 9

Analytical envelopes for a sinusoidal pressure disturbance with: a constant amplitude (blue), linear growth (purple), linear decay (red) and the equivalent envelope with the average growth (grey); b constant amplitude (blue), sinusoidal modulation (red) and the equivalent envelope for a constant-amplitude ramp-like pressure disturbance (grey). The black dashed line is the equivalent maximum growth factor of the sinusoidally modulated, sinusoidal pressure disturbance. Insets show the dimensionless pressure-forcing amplitude as the forcing moves across the basin in numerical simulations

For a sinusoidally modulated atmospheric pressure forcing that grew, matured and decayed over time T, the resultant envelope is shown in Fig. 9b. Analytical solutions show that when a pressure disturbance returns to 0 amplitude at x = L (x* = 10), the simulated wave amplification would be η* = 20, giving a mean growth factor $\bar{\mu } = 2$. This was also reinforced by simulation 43. Interestingly, a sinusoidally modulating, sinusoidal disturbance produces the same amplitude wave at x = L as a constant amplitude, piecewise linear disturbance, the amplitude of which was first derived by Hibiya and Kajiura (1982).

These one-dimensional results suggest that a wave can occur when the amplitude of the atmospheric forcing is 0 at x = L. This idealised model is analogous to the real-world case that a wave could occur with no measurable atmospheric forcing at the coastline. Therefore, there may be no strong relation between meteotsunami wave heights and forcing magnitude at coastlines. Rather, several oceanographic measurements might be necessary to infer correlation between the time-integrated forcing magnitude and the final wave height. For similar reasons, we also speculate that only using in situ land observations as atmospheric-forcing indicators may lead to underpredicting meteotsunami occurrences in climatologies.

5.4 Forcing aspect ratio (2D-FD)

Although strict Proudman resonance assumes one-dimensional forcings (Proudman 1929), observed meteotsunami-generating atmospheric surface forcings are two-dimensional (e.g. Wertman et al. 2014). We investigate the direct effect of two-dimensionality on wave generation through Proudman resonance by varying the pressure-forcing aspect ratio A_P in simulations 44–49. The aspect ratio is defined here as the cross-propagation wavelength divided by along-propagation wavelength, such that A_P = λ_y/λ_x. (See Fig. 1 for visual representation of A_P.)

In this study, we investigate the effect of A_P by changing the cross-propagation wavelength, whilst maintaining along-propagation speeds appropriate for strict Proudman resonance (U = ω/k = c) and a constant along-propagation wavelength. The forcing was applied over a domain L = 100 km, W = 100 km, H = 100 m, with a 200-m horizontal grid spacing and 1-s time step. The forcing had along-propagation wavelength λ_x = 10 km. The cross-propagation wavelength was changed between 10 km ≤ λ_y ≤ 500 km, corresponding to 1 ≤ A_P ≤ 50 (Table 1, Supplementary Figure S8).

Wave amplifications were closely approximated by strict Proudman resonance at the centre of the forcing when A_P ≥ 10 (simulations 48–49, λ_x = 10 km, λ_y ≥ 100 km). As the aspect ratio decreased, the amplitude at the centre of the forcing also decreased (simulations 44–47, Table 1, Fig. 10). When A_P = 1 (simulation 44), the maximum sea-level amplification at the end of the simulation was about five times smaller (x* = 9.6, η* ≈ 6.1) than predicted from strict Proudman resonance (x* = 9.6, η* = 9.6π ≈ 30.2).

Fig. 10

Aspect-ratio simulations summary from 2D-FD simulations across 1 ≤ A_P ≤ 10. Black dots are simulation maxima, joined by black lines (linear interpolation)

One reason that more circular forcings produced smaller waves than more linear forcings is found by analysing the amplitude of the forced wave at resonance. Inputting a forcing specified by Eq. 7 into the two-dimensional wave equation (found by rearranging Eqs. 4–6 and assuming η ≪ H) indicated that when U = ω/k = c, the forced-wave height η_F was proportional to the aspect ratio as

$$ \eta_{F} \propto 1 + A_{\text{P}}^{2} . $$

(19)

Therefore, the forced-wave height is limited for forcings moving at strict Proudman resonant speeds when there is a finite aspect ratio. Furthermore, circular forcings are inefficient at maintaining the one-dimensional velocity convergence required for Proudman resonance. This inefficiency is seen partly as free waves spreading in the cross-propagation direction. Interestingly, our envelopes are similar to the wave envelopes of Niu and Chen (2019), who showed that whilst two-dimensional pressure forcings transfer energy to growing waves, energy is simultaneously removed by spreading free waves. Nonetheless, these numerical simulations suggest that more linear systems preferentially generate meteotsunamis.

The aspect ratio derived from radar reflectivity, A_R, defined as the ratio between the major and minor axes of an ellipse fitted to radar reflectivity, is often used to classify observed mesoscale atmospheric systems (e.g. Fairman et al. 2016, 2017). Typically, more circular systems may be represented with A_R less than about 3 and more linear systems with A_R more than about 3–5 (Liu and Zipser 2013; Fairman et al. 2016, 2017). Note that A_P ≠ A_R but A_P and A_R should be somewhat proportional. For example, radar can be used to indicate locations of high pressure in linear convective systems, as high pressure can occur in convective precipitation due to evaporation (Markowski and Richardson 2011). Nonetheless, the extent of radar reflectivity is not perfectly related to the atmospheric pressure forcing (e.g. Wertman et al. 2014). However, we speculate that radar reflectivity may provide observational evidence as to whether more linear systems preferentially generate meteotsunamis.

6 Conclusions

In this study, we extended the theory of strict Proudman resonance to include tidal elevation, tidal currents, bathymetric slopes, varying forcing speeds and varying forcing amplitudes and showed the effect of forcing two-dimensionality on Proudman resonant wave growth. The numerical model baseline simulations of strict Proudman resonance agreed to within 0.12% of analytical solutions. We explained the strict Proudman resonance sea-level elevations as a wave resulting from a forcing moving at the shallow-water wave speed. This wave grew linearly according to a wave envelope with constant gradient μ ≈ π. For waves that grew near-Proudman resonance, we generalised this explanation as a wave propagating with an average of the forced-wave and free-wave speed $W(x - \bar{U}t)$ multiplied by a wave envelope $E(x)$.

A hierarchy of simulations was used to examine tidal effects on wave growth. First, uniform depth changes were investigated. Wave amplifications decreased with nonzero tidal elevation because water depth changes made the free-wave speed deviate from the forcing speed. These results suggested that wave growth was slightly smaller at low tide than high tide.

Second, uniform currents caused wave amplifications to decrease compared to strict Proudman resonant growth. This amplification decrease was primarily because currents made the free-wave speed deviate from the forcing speed, but wave-flux conservation also slightly changed wave amplitude. Envelopes were different for the same magnitude current whether the wave was moving with or against the current. These differences were because wave-flux conservation changed 1) free and forced-wave amplitudes and 2) the free-wave wavelength.

Third, uniform currents and tidal elevation were modelled together. Counter-currents and increased water depth permitted wave growth greater than Proudman resonance, termed super-resonant growth. This super-resonant growth was because water depth increased free-wave speed and counter-currents almost equivalently decreased the free-wave speed. This wave speed compensation meant that the Froude number was near 1, whilst wave-flux conservation further amplified waves.

Fourth, sloping bathymetry was modelled with simulations that isolated the slope effect. The wave growth was better approximated using an effective free-wave speed rather than the average free-wave speed. This effective free-wave speed was the average free-wave speed plus the speed difference that was calculated to give the correct maximum separation of the forced and free wave. The largest waves were created with gentle upward sloping bathymetry, because the effective Froude was near 1 and waves shoaled to conserve wave flux (Green’s law).

Finally in the oceanographic section, a dynamic M₂ tide was simulated with forcings coinciding with low tide, rising tide, high tide and falling tide. The largest wave was modelled at falling tide, where super-resonant growth occurred that was 10% larger than strict Proudman resonance. This super-resonant growth was because the forcing speed approximated the tidal-wave speed and flux conservation further increased amplification.

Next, atmospheric-forcing factors were investigated. Determining average forcing speed may be the largest uncertainty in determining Proudman resonance. However, variable atmospheric-forcing speeds (with average speeds appropriate for Proudman resonance) may still produce near-Proudman resonant wave growth if the effective Froude number is near 1. We found that for linear bathymetric slopes and linearly varying forcing speeds, the calculation of the effective Froude number was the same. For sinusoidal forcing speeds, the effective forcing speed showed that rapidly changing forcing speeds (high N_u) with small variations (small ΔU) more closely approximated Proudman resonance than slowly changing forcing speeds with large variations. This relationship may explain why atmospheric systems with variable speeds and sloping bottoms can still produce near-Proudman resonant wave growth even though Proudman resonance conditions (0.9 ≤ Fr ≤ 1.1) are relatively rarely met.

Near-Proudman resonant growth occurred when the instantaneous Froude number varied between 0.82 and 1.18 because the effective Froude number was near 1. Commonly, instantaneous Froude numbers between 0.9 and 1.1 are used to indicate Proudman resonant regions in case studies. From these simulations, we speculate that instantaneous Froude numbers between 0.9 and 1.1 may be too conservative, and this range may be expanded to instantaneous Froude numbers of about 0.8–1.2.

By varying the amplitude of forcings that move at Proudman resonant speeds, waves grew according to the time-integrated forcing amplitude. These results suggest that there is no necessary relation between an instantaneous, point-measured forcing amplitude and wave height. Therefore, using only sparse, coastal measurements for atmospheric-forcing verification in climatologies may systematically reduce the number of identified meteotsunamis.

Finally, the simulations presented here suggested that more circular forcings (i.e. aspect-ratio forcings near 1) are less effective at producing Proudman resonant wave growth than more linear forcings (i.e. higher aspect-ratio forcings). A question follows from these simulations: Are meteotsunamis preferentially generated by higher aspect-ratio systems rather than lower aspect-ratio systems? If future observational analyses show that higher aspect-ratio systems preferentially produce meteotsunamis, it is unknown if this relation would occur because of direct alteration to resonance mechanisms (as suggested here) or for other reasons, such as greater system stability increasing coupling time or higher average forcing amplitudes leading to larger waves.

Proudman resonant wave growth is mainly dependent on the forcing speed (i.e. the forced-wave speed) and the free-wave speed matching. For a wave to grow from Proudman resonance, factors that affect the average speed are more important than factors that affect variability around the average speed. The measurable factors investigated here that affect the average wave speeds are of about the same importance, and their total effect on wave speeds and wave-flux conservation should be considered together. However, from these simulations, tidal elevation changes had the smallest effect on Proudman resonance, and from the literature, the most challenging to measure is the average forcing velocity. The aspect ratio is probably less important for wave growth than forcing and free-wave speeds matching, though the aspect ratio may determine whether a wave efficiently grows, or instead spreads. The average forcing amplitude is not important for efficient Proudman resonance. However, larger average forcing amplitudes will produce larger waves. Combined, these results suggest that the average forcing properties whilst over water and the average free-wave speed are most important to understand wave growth through Proudman resonance.