1 Introduction

The year 2021 will mark the 40th anniversary of the first work on contaminant source identification in aquifers: the Ph.D. thesis defended by Steven Gorelick at Stanford University (Gorelick 1981). The subject attracted some attention in the following decade. It flourished during the last decade of the previous century, and has grown exponentially during the current century; unfortunately, this growth has not been accompanied by the breadth of new ideas and approaches that took place between 1991 and 1997. Figure 1 shows a histogram of the number of works published in the field per year and its cumulative version. The figure includes a few papers not precisely about identifying contaminant sources in aquifers but in streamflows, lakes, and water distribution systems, mainly when these papers are based on the findings in aquifer research. As this paper is being written, the total number of works found is 157, but that number most likely will have increased by the time the paper is published.

Fig. 1
figure 1

Histogram and cumulative histogram of the number of papers published on the subject of contaminant source identification. Total number of papers is 157

Full size image

The rate at which papers have been published in the last 3 years is above 10 papers per year, yet very few discuss applications to real problems.

Fig. 2
figure 2

Timeline with the papers that marked a difference in the solution of the contaminant source identification problem. The unlisted years are those without any published work. The reddish years correspond to major breakthroughs and the orangish years to minor ones

Full size image
Fig. 3
figure 3

Time-varying pulse injection used by Skaggs and Kabala (1994) and repeatedly used later as a benchmark problem

Full size image
Fig. 4
figure 4

Histograms of the number of papers classified by the dimensionality of the case studies

Full size image
Fig. 5
figure 5

Name cloud of all last names of authors signing the papers

Full size image
Fig. 6
figure 6

Papers by country of first-author institution

Full size image

This paper revisits how the subject has evolved after the pioneering work by Gorelick (1981), pointing out those papers that, in the authors’ opinion, signified an apparent breakthrough in the subject. The paper ends with a discussion of why, after 40 years, the subject is not mature enough to find routine applications to real cases and is still far from being applied regularly.

2 The Problem

The problem of identifying a contaminant source in an aquifer using concentration measurements observed downgradient from the point of contamination falls within the realm of inverse problems (Tarantola 2005; Zhou et al. 2014). Consider, first, a forward model

$$\begin{aligned} \mathbf {d}=\mathbf {G}(\mathbf {m}), \end{aligned}$$
(1)

where \(\mathbf {d}\) is the outcome of the model providing the state of the system, \(\mathbf {m}\) represents the model parameters at large, including both material parameters and those variables that need to be specified to characterize the system before any prediction is performed, and \(\mathbf {G}\) is the function that maps parameters into system states. For example, in an aquifer where groundwater flow is under study, the state of the system is given by the piezometric heads, the model parameters are the hydraulic conductivities and porosities, but also the infiltration rates, boundary conditions, and pumping rates; and the function \(\mathbf {G}\) is the groundwater flow equation, or better, the numerical model solving the groundwater flow equation on a discretized version of the aquifer.

Consider, now, that several observations of the state of the system are available, \(\mathbf {d}_{\text {obs}}\); one could attempt to guess the values of the model parameters by inverting (1)

$$\begin{aligned} \mathbf {m}=\mathbf {G}^{-1}(\mathbf {d}). \end{aligned}$$
(2)

This inversion is much more challenging to perform than the forward modeling, because seldom is the inverse model \(\mathbf {G}^{-1}\) explicitly known, or the number of necessary observations available. In such case, the solution is to use the forward model to try to determine the parameters by means of an optimization or search procedure. During the search, the objective is to find a set of parameters \(\mathbf {m}\) that produces state values \(\mathbf {G(m)}\) that are as close as possible to the observed ones. Issues that must be considered in solving this problem include taking into account measurement errors—observations \(\mathbf {d}_{\text {obs}}\) may be corrupted estimates of the true state values—and model errors—\(\mathbf {G}\) is only a numerical approximation of a system state equation that may not represent exactly all relevant processes, and therefore, predictions \(\mathbf {d}\) may not be exactly of the system state.

Contaminant source identification is an inverse problem where the target parameters to identify are the number and spacetime locations of the contamination events and their strengths. As discussed next, focusing on identifying the parameters characterizing the source results is an interesting and difficult-to-solve problem. Still, it may remain purely academic if realism is not introduced as part of the solution to the general problem.

3 Milestones Along the Timeline

3.1 Early Work: The Simulation–Optimization Approach

The Ph.D. thesis by Steven Gorelick (1981) centers on groundwater pollution management problems, one of which is determining the location and strength of a contaminant leaking into an aquifer, making this the first work addressing this problem. The work was later published (Gorelick et al. 1983) and, to the best of the authors’ knowledge, is the first paper on the subject.

The problem addressed is identifying the locations and strengths of the leaking portions of a pipe that is in contact with an aquifer where the contaminant disperses. The problem is cast as an optimization problem to minimize an objective function measuring the discrepancy between model-predicted concentrations and those that are observed

$$\begin{aligned} J(\mathbf {m}) = \mathbf {w}\left[ |\mathbf {d}_{\text {obs}}-\mathbf {d}_{\text {cal}}|^p\right] ^\mathrm{T} \end{aligned}$$
(3)

with

$$\begin{aligned} \mathbf {d}_{\text {cal}} = \mathbf {H}\mathbf {d} = \mathbf {H}\mathbf {\mathbf {G}(\mathbf {m})}, \end{aligned}$$
(4)

where \(\mathbf {d}_{\text {obs}}\) is a vector with the observed concentrations, and \(\mathbf {d}_{\text {cal}}\) is a vector with the calculated concentrations at the same locations, which are obtained after applying an observation matrix \(\mathbf {H}\) to the model outcome \(\mathbf {G}(\mathbf {m})\); \(\mathbf {w}\) is a row vector of positive weights, the exponent p is generally 1 or 2, depending on the norm to be minimized, and the upper-script T stands for transpose. In Gorelick’s work, he uses two optimization approaches, a linear programming one, in which the exponent is 1, and a least-squares one, in which the exponent is 2. In both cases, the weights are inversely proportional to the magnitude of the observations.

The vector of parameters \(\mathbf {m}\), on which \(\mathbf {d}\) depends, includes all the parameters needed to run the numerical model \(\mathbf {G}\), such as the material parameters describing the aquifer (conductivity, porosity, etc.), the boundary conditions, the external stresses, and the parameters describing the source. Not all of these parameters are subject to identification, and in most papers, many of them are considered known without uncertainty. For example, in the work by Gorelick, all model parameters are known (and homogeneous) except for the intensities at eight potential pipe leaks. Under these settings, application of the principle of superposition yields \(\mathbf {d}_\text {cal}\) as a linear function of the unknown parameters \(\mathbf {m}\); this allows to write the minimization problem as a linear programming one. Each observed concentration in time and space acts as a linear constraint to be satisfied by the parameters. Gorelick et al. (1983) also analyze the results obtained by multiple regression, which amounts to minimizing (3) with an exponent p equal to 2 using a least-squares approach. This paper sets the scene for the papers to come. Gorelick et al. (1983) had identified a new and interesting inverse problem. He also established a specific way to approach the problem, which is the combination of simulation—to solve the forward model (1)—and optimization—to minimize an objective function like (3). For this reason, the papers using this approach are referred to as simulation–optimization papers.

The Ph.D. thesis by Gorelick (1981) also got the attention of Hwang and Koerner (1983), who looked for an alternative solution to the problem of source identification coupled with a dynamic network design. They use system sensitivity theory (a branch of control theory). Aquifer transport is treated as a dynamic system for which an initial guess of parameters is made, and feedback is obtained after concentrations are observed. The mismatch between predicted and observed concentrations is used to compute a so-called trajectory function that provides a perturbation of the parameters to be added to their last estimate before making the next prediction. The authors demonstrated the method in a two-dimensional synthetic aquifer and announced that a three-dimensional case study would follow, which was never published.

The decade of the 1980s ended with the publication of a research report by Datta et al. (1989), who use the same approach as Gorelick et al. (1983) to solve the problem.

From here on, the text will focus on the papers that, according to the authors, have supposed a significant advancement either in the solution of the core problem or in making the solution closer to its potential application to real cases. These papers are indicated in the timeline shown in Fig. 2. The text will end with a quick discussion and classification of the papers published during these 40 years. Two tables, including all 157 papers, are appended as supplementary material.

3.2 Backward Probability

Bagtzoglou et al. (1991) formulate a probabilistic solution for the problem of source identification based on the stochastic transport theory by Dagan (1982). In a heterogeneous media, solute concentrations resulting from an injection of a contaminant at location \(\mathbf {X}_0\) are proportional to the probability that such a particle may be at location \(\mathbf {X}\) after some time t. Dagan’s theory revolves around trying to find these probability functions. Reversing the concept, one can think of finding the probability that a given particle that has been observed at \(\mathbf {X}\) at time t was at \(\mathbf {X}_0\) at time zero. When the release time is known, running a backward-in-time particle tracking using the current spatial distribution of the concentrations will yield a map of probabilities. The locations with the highest values would correspond with the source locations. As described, this identification is possible only if the velocity field is perfectly known and if all the sources start at the same known time. The paper leaves some unresolved issues but opens a new avenue for the solution of the source identification that will be subsequently explored by several authors.

Bagtzoglou et al. (1992) addressed some of those problems in their next paper, such as not knowing precisely the time of the release or the velocity field, and propose the calculation of location and time probabilities with attached uncertainty.

3.3 Joint Identification of Source and Hydraulic Conductivity

Wagner (1992) is the first author who realizes that assuming that the hydraulic conductivity or the velocity spatial distributions are known is unrealistic and proposes a maximum likelihood parameter estimation following the steps by Carrera (1984) and Carrera and Neuman (1986). The forward problem remains the same, but now the objective function depends not only on the source parameters, but also on other parameters such as hydraulic conductivities, dispersivities, and boundary fluxes, which must be identified as well. The author demonstrates the application of maximum likelihood estimation, which had been utilized successfully for aquifer parameter identification in zoned aquifers, to the simultaneous estimation of material and source parameters. Our main criticism of this work is that the conceptualization of aquifer heterogeneity is very simple. It is limited to two zones with homogeneous flow and transport parameters. It also assumes that the source location is known, with the only source-related unknown being the mass load. In total, there are 10 parameters to estimate.

The objective function to minimize in this work is the negative log-likelihood function, which under the assumption of normally distributed errors has an expression very similar to (3). Observations \(\mathbf {d}\), in this case, were not limited to concentration values but also included piezometric heads (to help in the hydraulic conductivity identification).

The simultaneous estimation of aquifer and source parameters will reappear in several papers published later, but, almost always, with very simplistic representations of aquifer heterogeneity.

3.4 Time-Varying Injection and Tikhonov Regularization

The next major step was to consider the identification of a continuously time-varying solute injection function. Until the work by Skaggs and Kabala (1994), the identification of a contaminant source was either of a constant pulse of finite duration or a series of them. Still, no one had contemplated the possibility of identifying a pulse that was a continuous function of time. In their one-dimensional seminal paper, Skaggs and Kabala proposed identifying the three-peaked release function represented in Fig. 3; the identification was formulated by discretizing the span during which the release occurred into 100 points. They argued that such identification would be bound to fail due to the ill-posedness of the inversion problem and introduced, for the first time, the idea of regularizing the solution. Regularization implies modifying the objective function (3) by adding a term

$$\begin{aligned} J(\mathbf {m}) = \mathbf {w}\left[ |\mathbf {d}_{\text {obs}}-\mathbf {d}_{\text {cal}}|^p\right] ^\mathrm{T} + \alpha ^2 \Vert L(\mathbf {m})\Vert ^2, \end{aligned}$$
(5)

where L is the regularization function and \(\alpha \) is a weighting factor controlling its strength in the objective function. Skaggs and Kabala’s regularization is a function of the 100 parameters discretizing the input function penalizing rapid oscillations in time. The authors focus exclusively on identifying the discretized source function, assuming that all other parameters controlling flow and transport in a homogeneous aquifer are known, including the source location. The observations are concentrations sampled in time and space at selected intervals. Two case studies were analyzed, one with exact observations without observation errors and one with inexact observations with measurement errors of varying magnitude. The authors conclude that Tikhonov regularization could be used to solve an inherently ill-posed inverse problem as long as the observation errors are not too large and the measurements are taken before the plume has dissipated too much.

3.5 Minimum Relative Entropy

The year 1996 saw the publication of two significant contributions to the solution of the source identification problem. One of them is the work by Woodbury and Ulrych (1996), who shifted the focus of the problem from a deterministic one into a stochastic one. The other one is described in the next section.

The parameters \(\mathbf {m}\) to be identified are considered as random variables with unknown probability distribution functions (pdfs), and the optimization approach is aimed at determining these pdfs, from which the expected value or the median could be retrieved as the model parameter estimate. Let p be the parameter prior pdf, which could be as uninformative as a uniform distribution between some lower and upper bounds, and let q be the pdf of the parameters that are consistent with the observation data. By consistent, it is meant that the expected value of the predicted state at observation locations be equal to the observed values, \( E\{\mathbf {H G (m)} \}=\mathbf {d}_\mathrm{obs}\). Pdf q will result from the minimization of the relative entropy

$$\begin{aligned} H(q,p)=\int q(\mathbf {x}) \ln \left[ \frac{q(\mathbf {x})}{p(\mathbf {x})}\right] \mathrm{d}\mathbf {x} \end{aligned}$$
(6)

subject to several linear constraints that result from the consistency requirement described above. The authors describe in detail how the minimization is performed, retrieve \({q}(\mathbf {m})\), and compute its expected value, which is compared with the reference injection curve with satisfactory results. The same injection function used by Skaggs and Kabala (1994) is analyzed, and the impact of observation errors is also studied. The location of the source is not subject to identification.

3.6 Heuristic Approaches

The work by Aral and Guan (1996) is the second of the landmark papers of 1996. It is the first paper that uses a heuristic approach to solve the optimization problem. The problem statement is the same one used by Gorelick et al. (1983), that is, the minimization of (3) subject to linearity constraints (one for each observed concentration). These constraints can be easily derived from the solute transport equation when the aquifer is homogeneous and of known parameters. The authors also add the additional constraint that the parameters to identify (the contaminant fluxes into the aquifer) must be positive. The originality of the solution is in departing from standard optimization algorithms and moving into the, then new, heuristic algorithms, of which a genetic algorithm was chosen. As with all heuristic algorithms, multiple evaluations of the forward model (1) are needed, which makes the method computationally demanding; as a counterpart, these heuristic algorithms are supposed not to get stuck in local minima and are capable of obtaining the global minimum for objective functions with potentially many local extremes. Aral and Guan (1996) demonstrate the application of genetic algorithms to identify the contaminant fluxes from six known locations time-varying stepwise in three known time intervals. The aquifer is synthetic, two-dimensional, and of known parameters. Exact and measurement error-corrupted observations are used. The authors conclude that genetic algorithms are a viable alternative.

3.7 Geostatistical/Bayesian Approaches

Following the path by Woodbury and Ulrych (1996), Snodgrass and Kitanidis (1997) also use a stochastic approach for the solution of the identification problem. The authors focus on the solution of the same problem, estimating a contaminant time-varying release function into an aquifer, assuming that the source location and the rest of the parameters describing the aquifer are known. Following a standard geostatistical approach, the parameters \(\mathbf {m}\) (which, in this case, are the injection strengths discretized in time over the injection period) are modeled as a random function with a stationary but unknown mean value and a stationary but unknown covariance function whose shape is known (for instance, it may be an exponential function). There are no observations of the parameters, but there are observations of the concentrations downgradient from the source, which, for conservative solutes, are linearly related to the source parameters. This linearity permits the computation of the conditional expected value and the conditional covariance of the unknown parameters given the observed concentrations.

The geostatistical approach starts by first estimating the parameters of the multivariate random function, which, in this case, are the unknown mean and the unknown parameters of the covariance function (variance and correlation length for the case of an exponential isotropic covariance). Then, the estimation is carried out, maximizing the likelihood of the observations given the structural parameters. Snodgrass and Kitanidis (1997) argue that simultaneous estimation of both mean and covariance parameters results in biased estimates, and proceed to maximize the likelihood after filtering out the unknown mean by integrating over all possible mean values. Once the parameters have been estimated, the rest is a standard co-kriging estimation to obtain the conditional (also referred to as posterior) estimate of mean and covariance of the parameters describing the injection function.

Since kriging cannot enforce non-negativity, Snodgrass and Kitanidis (1997) describe an iterative approach to the estimation of a nonlinear transform of the input concentrations (what breaks the linearity between parameters to be estimated and observations) that ensures that all concentration estimates are positive. The method is demonstrated using the benchmark injection function by Skaggs and Kabala (1994) in a one-dimensional aquifer with satisfactory results. An interesting discussion in the paper is the indication that Tikhonov regularization or thin-plate spline interpolation would yield the same results as the geostatistical approach for specific shapes of the covariance of the multivariate random function.

Although not explicitly stated in the paper, this is the first one in which a Bayesian approach is used.

3.8 Jumping into Three Dimensions

In 1998, the first paper addressing contaminant source identification in a three-dimensional domain was published. Woodbury et al. (1998) extend their application of minimum relative entropy (MRE) in one dimension to the reconstruction of a three-dimensional plume source. The source is a rectangular patch of known dimensions, and in order to maintain the linearity between observations and source concentrations, the aquifer is considered homogeneous and with known parameters. An analytical solution of the transport equation is used that relates aquifer concentrations and source values. The benchmark input function of Fig. 3 is used, and the capabilities of the MRE in three dimensions are demonstrated. Case studies using observations with and without errors and the interplay between spatial data and temporal data are analyzed.

The method was also applied to a real case to identify the source of a 1,4-dioxane plume observed at the Gloucester landfill in Ontario, Canada. The underlying model of the aquifer had to adhere to the simplifications used for the derivation of the algorithm; that is, it was modeled as homogeneous with known flow and transport parameters. The authors are quite satisfied with the results, since the resulting parameter uncertainty intervals are smaller than previous estimates.

3.9 Artificial Neural Networks

It is not until 2004 that the first paper appears that explores the potential of machine learning to identify a contaminant source. Singh et al. (2004) and Singh and Datta (2004) publish two very similar papers to demonstrate the use of artificial neural networks to estimate the parameters describing a contamination event and the aquifer properties. Focusing on the joint identification problem, the authors consider that aquifer and source can be characterized with 14 parameters: one for the isotropic conductivity, one for porosity, two for dispersivity (longitudinal and transverse), and 10 for the injection strengths over 5 years at two locations (injections remain constant within the year). The aquifer is two-dimensional and homogeneous in its parameters and perfectly known in size and shape; the location of the two sources is also known. Using a numerical code, the authors generate 8,500 sets of values for the 14 parameters, which are used to predict concentrations at 40 time intervals at four observation wells. From these sets, 4,500 are chosen as training sets and 4,000 as testing sets. The authors consider different artificial neural network architectures until they find the one that produces the smallest prediction errors. They follow with a demonstration using data with observation errors and conclude that these models could be used for source identification, with a warning: the artificial neural network would have to be retrained for a different case study or if the aquifer system changes in any way.

3.10 Markov Chain Monte Carlo and Surrogate Models

The work by Zeng et al. (2012) marks a new development that goes beyond an incremental contribution. The problem is cast in a probabilistic framework aimed at computing the posterior probability of the parameters (location and strength source) given the observations (concentration measurements) using a Bayesian framework

$$\begin{aligned} p(\mathbf {m}|\mathbf {d})=\frac{p(\mathbf {m})p(\mathbf {d}|\mathbf {m})}{p(\mathbf {d})}, \end{aligned}$$
(7)

where \(p(\mathbf {m}|\mathbf {d})\) is the posterior pdf, \(p(\mathbf {m})\) is the prior pdf, \(p(\mathbf {d}|\mathbf {m})\) is the likelihood, and \(p(\mathbf {d})\) can be regarded as a normalizing constant. Then, instead of using the geostatistical approach to determine the posterior pdf, the authors propose two novelties: one to use Markov chain Monte Carlo (McMC) to sample the posterior distribution, and the other to use a surrogate model for the forward problem (1) (since McMC requires many evaluations of the likelihood function, which, in turn, requires many runs of the forward model). In particular, the McMC algorithm chosen is delayed rejection combined with an adaptive Metropolis sampler as described by Haario et al. (2006). The surrogate model chosen is a sparse grid-based interpolation using the Smolyak algorithm (Wasilkowski and Wozniakowski 1995), which provides an estimate of the forward model by interpolating the forward model values computed on a sparse grid in parameter space. Let N be the number of parameters in \(\mathbf {m}\); a grid of points is defined within the parameter domain \(\{m_{i_1},m_{i_2},\ldots ,m_{i_n}; i_1=1,\ldots ,Q_1, i_2=1,\ldots ,Q_2,\ldots ,i_N=1,\ldots ,Q_N\}\), where \(\{Q_1, Q_2, \ldots Q_N\}\) are the number of points along each dimension. The forward problem is evaluated at each of these points, and then the forward problem is estimated at any point by interpolating these values using some predefined basis functions

$$\begin{aligned} \mathbf {G}(\mathbf {m}) \approx \sum _{i=1}^Q f_\mathbf {m_i}(\mathbf {m}) \mathbf {G}(\mathbf {m_i}), \end{aligned}$$
(8)

where Q is the number of surrounding points to use in the interpolation, and \(f_\mathbf {m_i}(\mathbf {m})\) are the basis functions. How to select the number of points to use, the grid on which they are defined, and the basis functions is discussed in the paper.

The authors analyze two synthetic two-dimensional case studies, one with five unknown parameters, namely, location coordinates, beginning and ending times, and source strength, and the other one with 10 parameters representing the source strength variability in time. Another difference between the two cases used to test the surrogate model is that the first case uses a homogeneous aquifer and the second a heterogeneous one, although conductivities are not subject to identification and therefore assumed known. Nevertheless, in both cases, the algorithm can retrieve the parameters sought.

3.11 Network Design

Jha and Datta (2014) introduce a component of realism that had only been treated in a very imprecise way by Hwang and Koerner (1983), and mentioned without any demonstration in the review by Amirabdollahian and Datta (2013): that of designing the monitoring network to identify the source at the lowest observation cost possible. Even though the aquifer was still modeled as homogeneous and perfectly known, the authors propose a realistic situation in which there is not a network of observation locations already in place, but rather, a contaminant is observed in a well during a period. Then, a network of observations is deployed, maximizing the chances of correctly detecting the source locations and magnitudes. The method proposed involves two stages. In the first stage, once the contaminant has been monitored during a specific time in the detection well, several potential source locations, which are consistent with the observations, are identified in the aquifer. Then, with this set of potential sources, a dense grid of potential observation locations is designed out of which a small number of points are chosen as the observation network. This network is defined to maximize the possible observed concentrations coming from the potential source locations. Once the network has been defined, concentrations are collected in the newly designed network and used as data to solve the source identification problem. This problem is solved by a simulation–optimization approach in which the objective function (3) is written in terms of a dynamic time warping distance, a distance that coincides with the traditional Euclidean distance when two series of values spanning the same length, with the same number of samples, and without missing data are compared. The authors demonstrate the effectiveness of optimal network design for identifying a time-varying contaminant source in their synthetic aquifer.

3.12 Ensemble Kalman Filter and Joint Identification of Source and Hydraulic Conductivity

The ensemble Kalman filter (EnKF) (Evensen 2003) had been used for parameter identification in petroleum engineering and hydrogeology for some time (Aanonsen et al. 2009; Chen and Zhang 2006; Li et al. 2011a, 2012; Xu et al. 2013a, b), but focusing on static parameters such as hydraulic conductivities. The EnKF is an assimilation technique based on gathering observations in time and updating the parameter estimates after each collection step. Comparison of the forward model predictions and the observations allows the correction of the estimates into a newly updated estimate for the next forward prediction. However, when the parameter to be estimated is the location of a contaminant source, an updated location cannot be incorporated into the model to predict in time unless the forward model is restarted from time zero to account for the updated location. This procedure is known as the restart EnKF (r-EnKF). Xu and Gómez-Hernández (2016) demonstrated that the r-EnKF can be used for source identification and went a step further (Xu and Gómez-Hernández 2018) to prove that a channelized heterogeneous hydraulic conductivity spatial distribution could be jointly identified with the contaminant source parameters (location, release time, and source strength).

At last, after many years, a true leap towards the applicability of contaminant source identification algorithms was achieved, since, for the first time, a complex, realistic spatial distribution of hydraulic conductivity was not assumed known and was subject of identification simultaneously with the source. However, the rest of the parameters defining the aquifer, such as porosity, dispersivity, boundary conditions, and stresses, were known.

3.13 Bayesian Model Selection

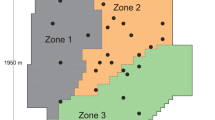
The paper by Cao et al. (2019) is the last paper that proposes a new paradigm to address the problem of contaminant source identification. As most of the papers published before that use synthetic experiments, the reference data were obtained adopting a specific model for the aquifer (whether deterministic or probabilistic). Then the same model was used for the solution of the identification problem. In a real situation, the uncertainties around the aquifer model are significant, and it is virtually impossible to claim that the aquifer system is known. Cao et al. (2019) adopt a probabilistic model to select among a set of potential aquifer models using a Bayesian approach. The feasibility of the approach will depend on the span covered by the alternative models proposed. The authors demonstrate their proposal in two synthetic case studies. One is a two-dimensional aquifer with a zoned spatial distribution for hydraulic conductivity. The other is a three-dimensional experiment in a laboratory column made up of two sands arranged in two continuous blocks of very different shapes and sizes. The different models considered are not so different after all; in both case studies, the models differ only in the size and shape of the zones used to describe the heterogeneity of the hydraulic conductivity, but the paper marks a route for how to incorporate different descriptions of the aquifer system and to identify both the model description and the source parameters that best reproduce the observations.

4 But There Are More Papers

In the previous sections, the papers that marked a change in the line of research towards the solution of contaminant source identification have been discussed. However, there are more: all in all, 157 papers have been encountered, and they deserve a short analysis that will help place the whole research field in perspective. Table 1 in the Supplementary Material lists the papers and highlights their main contributions, while Table 2, also in the Supplementary Material, uses the same paper numbering as Table 1 and includes some characteristic features of the papers of interest. More precisely, Table 2 includes the dimensionality of the problem, the type of source, whether or not the source is time-dependent (it is marked as time-dependent if it is a continuous function of time as in Fig. 3 or a step function that changes according to some stress periods; it is marked as time-independent if it is either a pulse or a continuous injection), the type of solution algorithm used to solve the identification problem, the state equation considered with indication of the code used to solve it when available, the type of case study analyzed (it could be synthetic, laboratory, or field), the parameters describing the source being identified (the most common parameters are the source locations and the release functions; in some occasions, the locations are chosen out of a set of release candidates or the strength of the source changes stepwise according to predefined stress periods), whether other parameters apart from the ones describing the source are identified (some papers also identify flow and transport parameters, although in most of them these parameters are homogeneous or piecewise homogeneous within the domain), and finally, whether hydraulic conductivity was considered as a heterogeneous parameter, and if heterogeneous, whether this heterogeneity was piecewise, that is, variable but homogeneous within well-defined zones, and whether the heterogeneity was known or was subject of identification as well.

Analyzing these attributes for all the papers, we can see an evolution towards applicability that looks more like the upper limb of a logistic curve reaching its asymptote than the exponential rise in the number of papers published.

Next, the different attributes will be discussed, stressing the potential applicability of the results to real problems.

4.1 Dimensionality

While the first papers presented applications in two-dimensional aquifers, a substantial number of papers continue to be published that address the problem in one dimension. Figure 4 shows the histograms of the papers classified by their dimensionality. It is not until 1998, with the paper by Woodbury et al. (1998), that the first three-dimensional analysis is published. The majority of papers are for two-dimensional aquifers, and only in the past few years have applications in three dimensions increased.

From a practical point of view, solutions are needed in two or three dimensions. The scale of the problem will determine the need to use a two-dimensional model (regional flow) or a three-dimensional one (local flow).

4.2 Source

The problems addressed by the different authors can be classified as single or multiple sources and as point, areal, or volumetric sources. Some authors assume that the source locations are known or that the source locations should be chosen out of a set of possible locations. This situation could be plausible in some occasions when the agent originating the contamination in the aquifer is known, but in many instances this is not the case, and the location must be treated as an unknown to be identified. The case of multiple locations where the number and coordinates of the sources have to be jointly identified has not been addressed. When multiple sources are considered, there are some potential source locations to choose from, what transforms a difficult continuous-mixed-integer optimization problem into a not much simpler combinatorial one.

The papers for which the type of source is identified as areal consider the shape of the area to identify as known and only seek the release strength, except for Ala and Domenico (1992), Mahinthakumar and Sayeed (2005), Hosseini et al. (2011), Ayvaz (2016), and Zhou and Tartakovsky (2021) who also attempt to find the shape of the areal source. Only two of these consider an unknown generic shape.

Of the papers addressing a volumetric source, all assume that the shape is known, except for Mahinthakumar and Sayeed (2006), Mirghani et al. (2009), Aghasi et al. (2013), Jin et al. (2014), and Yeh et al. (2016), who also attempt to identify the shape of the source, with most using a simple prismatic parameterization.

From a practical point of view, it does not seem feasible (because of its difficulty) to ask for a solution in which the sources are unknown in number, locations, and shapes, but some degree of lack of knowledge regarding these three attributes will always be present, and methods should aim to address all three in the most general way possible.

4.3 Time Dependency

When the source varies in time, even if it is a single point at a known location, the difficulty of the identification problem increases dramatically, unless the variation is very simple and can be parameterized with a few unknowns (as is the case of a rectangular pulse or a train of pulses that only needs each pulse beginning and end times and the pulse concentrations).

A substantial number of papers consider that the source is either an instantaneous injection or a continuous one of constant intensity, in which case only two parameters are needed to describe it: the (initial) time of the release and its concentration. Adopting this type of release means that there is good knowledge of what happened, as it could be the case of an illegal overnight dump into an abandoned well or continuous leakage out of a deposit. These cases are labeled as not being time-dependent.

Another important number of papers assume that the concentration history varies stepwise in time according to several stress periods. The duration of each stress period is known, and during each period, the concentration remains constant. Unless the stress periods are considered relatively short in time, the number of parameters to describe the time dependency is relatively small; adopting this formulation also implies that there is essential knowledge about the history of the release and the time periods during which the release remained constant. In Table 2, care has been taken to indicate when the case study assumes that the source strengths are identified at specified stress periods.

Finally, another group of papers attempts to identify an unknown continuous-time function that describes the release. This group starts with the one-dimensional case by Skaggs and Kabala (1994) for which the location was known, and continues with papers in higher dimensions and the simultaneous identification of the source location (Todaro et al. 2021).

4.4 Solution Approach

As already noted in the section describing the landmark papers, there are three main approaches to address contaminant source identification: the simulation–optimization approach, the backward probability tracking approach, and the probabilistic approach.

Most of the efforts over these 40 years since the first paper was published have focused on solving the identification problem under the premise that some concentration observations are available (in space and time), and there is a need to determine the parameters that describe the originating contamination, with little consideration of trying to account for other uncertainties inherent to groundwater flow and mass transport. Many refinements have been proposed concerning the initial papers, with the latest papers making use of the most sophisticated techniques regarding optimization by heuristic approaches, machine learning to build surrogate models, and innovative applications of Markov chain Monte Carlo.

It can be concluded that the identification problem is solved provided that there is perfect knowledge of the underlying aquifer in which the contamination has occurred. However, when uncertainties about the parameters describing the aquifer are considered, no approach has been able to get close enough to real conditions to warrant its routine application to field cases.

4.5 State Equation

The state equation information included in Table 2 highlights whether flow and transport were solved, or just transport assuming the flow velocity is known; it makes reference to the codes used to solve the state equation, when known, and in the most recent years, whether surrogate models have been used to speed up the multiple evaluations of the forward problem needed by most of the solution algorithms.

4.6 Case Study

Five papers have used laboratory data, 28 papers used field data, and 113 papers used synthetic data. Although the number of papers using field data has increased in the last few years, the corpus of the subject is mainly based on results using synthetic aquifers.

While synthetic aquifers are necessary to test new algorithms and techniques, the subject should be mature enough to prove the latest development in closer-to-field conditions. Besides, most of the papers using field data do not use the most elaborate techniques at the time, but generally make rather simplistic approximations, weakening the contribution of the field case demonstration.

More research with field data is needed. A task that on most occasions is hindered by the difficulty in having access to data that can be shared publicly. This may explain the relatively low number of field papers, but that does not explain the even lower number of papers using laboratory data.

4.7 Source Parameters Being Identified

It is important to note that not all papers attempt to identify the source location; many assume it is known, and many assume that it could be one of a small set of candidates. The rest of the papers identify the source coordinates, either a point in space or a small set of parameters that identify an areal or volumetric source.

The time distribution of the source strength was already discussed above.

The hardest problem is the simultaneous identification of the number and the locations of multiple sources, and it has not yet been addressed by anyone. Only a very recent paper considers the problem of identifying the location of two sources (the number of sources is therefore known) and the parameters describing them (Zhou and Tartakovsky 2021).

4.8 Other Parameters Being Identified

In practical terms, the aquifer parameters are never known, and therefore they should be subject to identification. Some authors consider that all parameters other than the source ones are known, without entering into any consideration of whether or not this decision is meaningful; some authors argue that they work with previously calibrated aquifer models, not using the additional concentration data to further refine the aquifer model calibration; finally, a few of the authors do perform a simultaneous identification of source and aquifer parameters.

When in Table 2 it is indicated that other parameters are identified, these additional parameters are described in Table 1.

4.9 Hydraulic Conductivity Heterogeneity

Hydraulic conductivity heterogeneity is of paramount importance for the proper prediction of contaminant transport (Capilla et al. 1999; Gómez-Hernández and Wen 1994; Li et al. 2011b). For this reason, it is necessary to include a realistic representation of conductivity if the techniques developed are to be applied in practice. The papers have been classified as not accounting for heterogeneity (N), accounting for heterogeneity using a zonation with constant conductivities within each zone (Z), and accounting for heterogeneous conductivity using a stochastic realization (Y).

However, using a heterogeneous conductivity is not enough to make the analysis realistic. The conductivity field cannot be perfectly known, so an additional set of papers is tagged as accounting for heterogeneity but not fully knowing the hydraulic conductivity spatial distribution (YN). Of these papers, the subset that additionally attempts to identify the unknown conductivity field contains the ones closest to applicability. The number of papers meeting these latter conditions—that is, that assume that conductivity is fully heterogeneous in space, unknown (except for a few sampling points), and subject to identification—is only 11. The techniques described in these papers are closer to being applicable in field conditions.

4.10 Additional Information

Figure 5 shows a word cloud with the last names of all authors signing the papers. While some of the last names of the Chinese authors may correspond to several people, it is clear that some authors have made an imprint in the field, with Datta being the leader and responsible for the fact that India and Australia are in third and fourth positions in the number of papers published by country, respectively.

Figure 6 shows a histogram of the number of papers published by the country of the first author institution. The United States has produced the largest number of papers overall, but if these numbers are broken down by year of publication, it is noticeable that China is the leader in the most recent years.

5 Conclusions

The productivity in terms of the number of papers published in the subject has grown exponentially in the 40 years since the first work. Unfortunately, this exponential growth in number is not paralleled by similar growth in added value. The field seems to be stalled, with only minor incremental advances towards a solution that can be applied with reasonable expectations to field cases.

From a practical point of view, it seems unreasonable to attempt to solve a source contamination identification without any prior knowledge about the source itself. The optimal method should identify all parameters at once: the number of contaminant events, their locations, their extent, and their time history. However, no one has tried to do it, and likely no one will, since it is too complex a problem. Therefore, it must be admitted that some information about the source is available, such as the number of sources, their potential locations, whether or not it is punctual, and if it is not punctual, some idea about the shape or the duration of the contamination event.

At the same time, from a practical point of view, it seems unreasonable to develop new techniques that do not incorporate the inherent uncertainties involved in groundwater flow and mass transport modeling. Thus, whatever technique that wishes to have a chance of being applied in practice has to incorporate the uncertainty on the parameters describing flow and transport and other variables such as infiltration, pumping, or boundary conditions. Also, these techniques should consider proper data acquisition, since many of the papers assume dense networks of observations already existing before detecting the contaminant.

There is still room for improvement, and for new papers on the subject, but they should either propose a radically new approach to solving the problem or recognize the limitations of previous work regarding its applicability and advance towards it.