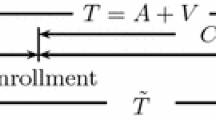Nonparametric and semiparametric estimators of restricted mean survival time under length-biased sampling

Abstract

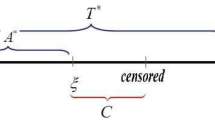
Restricted mean survival time is often of direct interest in epidemiologic studies involving censored survival time. In this article, we propose the nonparametric and semiparametric estimators of the mean restricted to the preassigned interval with censored length-biased data. Based on the peculiarity of length-biased data, the auxiliary information that truncation time and residual time have the same distribution is taken into account for improving estimation efficiency. For two-sample comparison, we construct two tests which are easy to implement. We also derive the asymptotic properties for the proposed estimators and test statistics. In simulation studies, some simulations are conducted to compare the performances of several approaches to estimate restricted mean and to assess the test statistics. In addition, our methods are applied to a real data example and some interesting results are presented.

Appendix

For simplicity, let $N_{i}(t)=\varDelta _{i}I(Y_{i}\le t)$, $R_{i}(t)=\frac{1}{2}\{I(A_{i}\le t \le Y_{i})+\varDelta _{i}I({\tilde{V}}_{i}\le t\le Y_{i}) \}$. K(t) denotes $\frac{1}{2}E\{I(A\le t \le Y)+\varDelta I({\tilde{V}}\le t \le Y)\}$. W(t) denotes $E\{\varDelta I(Y\le t)\}$. We impose the following regularity conditions:

• (a) J(t) and S(t) are absolutely continuous on $[0,\tau ^{*}]$, where $\tau ^{*}=\sup \{t:P(Y\ge t)>0\}$;

• (b) $\int _{0}^{\tau ^{*}}\frac{d W(u)}{K^{2}(u)}<\infty$ and $E\frac{1}{K^{2}(Y)}<\infty$;

• (c) The true regression parameter $\beta _{0}$ lies in a compact set ${\mathcal {B}}$, and X is bounded;

• (d) $\varLambda _{0}(t)$ is absolutely continuous on$[0,\tau ^{*}]$, and $\varLambda (\tau ^{*})<\infty$.

Lemma 1

Under the regularity assumptions (a) and (b) given above, when $n\rightarrow \infty$, the random process $n^{\frac{1}{2}}\{{\hat{\varLambda }}(t)-\varLambda (t)\}$ for $0<t<\tau ^{*}$ converges to a zero-mean Gaussian process with the variance–covariance function $\sigma _{\varLambda }(t_{1},t_{2})=E\{\phi _{1}(t_{1})\phi _{2}(t_{2})\}$.

Proof of Lemma 1

Let

$$\begin{aligned} K(t)= & {} \frac{1}{2}E\{I(A\le t \le Y)+\varDelta I({\tilde{V}}\le t \le Y)\},\\ W(t)= & {} E\{\varDelta I(Y\le t)\}. \end{aligned}$$

Their corresponding empirical processes are

$$\begin{aligned} K_{n}(t)= & {} \frac{1}{2n}\sum _{i=1}^{n}\{I(A_{i}\le t \le Y_{i})+\varDelta _{i}I({\tilde{V}}_{i}\le t \le Y_{i} )\},\\ W_{n}(t)= & {} \frac{1}{n}\sum _{i=1}^{n}\varDelta _{i}I(Y_{i}\le t). \end{aligned}$$

By the proof of Lemma 1 in Wang et al. (2017), the cumulative hazard function of ${\tilde{T}}$ can be derived as

$$\begin{aligned} \varLambda (t)=\int _{0}^{t}\frac{dW(u)}{K(u)}, \end{aligned}$$

and its estimator ${\hat{\varLambda }}(t)$ can be expressed as

$$\begin{aligned} {\hat{\varLambda }}(t)=\int _{0}^{t}\frac{dW_{n}(u)}{K_{n}(u)}. \end{aligned}$$

Note that $n^{1/2}\{W_{n}(t)-W(t)\}$ and $n^{1/2}\{K_{n}(t)-K(t)\}$ are sums of independent, identically distributed processes with mean 0. We can use empirical process theory to prove the weak convergence of them. Since $\frac{1}{2}\{I(A \le t \le Y )+\varDelta I({\tilde{V}}\le t \le Y)\}$ and $\varDelta I(Y\le t)$ belong to Donsker class by the Example 2.6.1 in Van Der Vaart and Wellner (1996), we can conclude the weak convergence of $n^{1/2}\{W_{n}(t)-W(t)\}$ and $n^{1/2}\{K_{n}(t)-K(t)\}$.

Applying the functional delta method (Andersen et al. 2012), we can derive the following asymptotic representation:

$$\begin{aligned}&\sqrt{n}\{{\hat{\varLambda }}(t)-\varLambda (t)\}\\&\quad =\sqrt{n}\int _{0}^{t}\frac{K(u)dW_{n}(u)-K_{n}(u)dW(u)}{K^{2}(u)}+o_{p}(1)\\&\quad =n^{-\frac{1}{2}}\sum _{i=1}^{n}\int _{0}^{t}\frac{dN_{i}(u)}{K(u)}-\int _{0}^{t}\frac{1}{2K^{2}(u)}\{I(A_{i}\le u \le Y_{i})\\&\qquad +\varDelta _{i}I({\tilde{V}}_{i}\le u \le Y_{i})\}d W(u)+o_{p}(1)\\&\quad =n^{-\frac{1}{2}}\sum _{i=1}^{n}\phi _{i}(t)+o_{p}(1) \end{aligned}$$

uniformly $t\in [0,\tau ^{*}]$, where

$$\begin{aligned} \phi _{i}(t)=\int _{0}^{t}\frac{dN_{i}(u)}{K(u)}-\int _{0}^{t}\frac{1}{2K^{2}(u)}\{I(A_{i}\le u \le Y_{i})+\varDelta _{i}I({\tilde{V}}_{i}\le u \le Y_{i})\}d W(u). \end{aligned}$$

$\{\int _{0}^{t}\frac{dN_{i}(u)}{K(u)}, t\in [0,\tau ^*]\}$ are monotone (increase with t) and its envelope function is square integrable by condition (b), thus it belongs to Donsker class with theorem 2.7.5 in Van Der Vaart and Wellner (1996). Similarly, $\{\int _{0}^{t}\frac{1}{2K^{2}(u)}\{I(A_{i}\le u \le Y_{i})+\varDelta _{i}I({\tilde{V}}_{i}\le u \le Y_{i})\}d W(u), t\in [0,\tau ^*]\}$ is a monotone function and bounded with $\int _{0}^{\tau ^{*}}\frac{d W(u)}{K^{2}(u)}$ , thus it is also a Donsker class. Combined with the Lemma 2.6.18 of Van Der Vaart and Wellner (1996), we can prove that $n^{\frac{1}{2}}\{{\hat{\varLambda }}(t)-\varLambda (t)\}$ converges to a zero-mean Gaussian process uniformly in $(0,\tau ^{*}]$. $\square$

The variance–covariance function of the limiting distribution, $\sigma _{\varLambda }(t_{1},t_{2})$, can be consistently estimated by ${\hat{\sigma }}_{\varLambda }(t_{1},t_{2})=n^{-1}\sum _{i=1}^{n}{\hat{\phi }}_{i}(t_{1}){\hat{\phi }}_{i}(t_{2})$, where

$$\begin{aligned} {\hat{\phi }}_{i}(t)=\int _{0}^{t}\frac{dN_{i}(u)}{K_{n}(u)}-\int _{0}^{t}\frac{1}{2K_{n}^{2}(u)}\{I(A_{i}\le u \le Y_{i})+\varDelta _{i}I({\tilde{V}}_{i}\le u \le Y_{i})\}d W_{n}(u). \end{aligned}$$

Lemma 2

Under the regularity assumptions (a) and (b), $\sup \limits _{0<t\le \tau ^{*}} |{\hat{\varLambda }}(t)-\varLambda (t)|$ converges to 0 in probability, when $n\rightarrow \infty$.

Proof of Lemma 2

Since every Donsker class is a Glivenko-Cantelli class with an application of Slutsky’s lemma, we can prove Lemma 2 easily with the result of Lemma 1. $\square$

Proof of Theorem 1

Considering estimation of $\mu _{\tau }$, $\sqrt{n}({\hat{\mu }}_{\tau }-\mu _{\tau })$ can be written as

$$\begin{aligned} \sqrt{n}({\hat{\mu }}_{\tau }-\mu _{\tau })= & {} \sqrt{n}\int _{0}^{\tau }{\hat{S}}(u)-S(u)du\\= & {} \sqrt{n}\int _{0}^{\tau }e^{-{\hat{\varLambda }}(u)}-e^{-\varLambda (u)}du\\= & {} -\sqrt{n}\int _{0}^{\tau }S(u)({\hat{\varLambda }}(u)-\varLambda (u))du+o_{p}(1)\\= & {} n^{-\frac{1}{2}}\sum _{i=1}^{n}\eta _{i}(\tau )+o_{p}(1), \end{aligned}$$

uniformly $\tau \in [0,\tau ^{*}]$, where $\eta _{i}(\tau )=-\int _{0}^{\tau }S(u)\phi _{i}(u)du$.

Combined with Lemmas 1 and 2, the weak convergence of $\sqrt{n}({\hat{\mu }}_{\tau }-\mu _{\tau })$ can be proved with continuous mapping theorem. Since the $\eta _{i}$ variates are independent and identically distributed with mean 0, applying the law of large numbers, ${\hat{\mu }}_{\tau }$ converges to $\mu _{\tau }$ in probability. $n^{1/2}({\hat{\mu }}_{\tau }-\mu _{\tau })$ converges weakly to Gaussian process with mean 0 and covariance $E(\eta _{i}(s)\eta _i(t))$ for $s,t\in (0,\tau ^*)$.

By this theorem, we easily derive that $n^{1/2}({\hat{\mu }}_{\tau }-\mu _{\tau })$ converges to a normal distribution with mean 0 and variance $E(\eta _i(\tau )^2)$ for $\tau \in (0,\tau ^*)$. $\square$

The variance of the limiting distribution, $E(\eta _{i}^{2})$, can be consistently estimated by $n^{-1}\sum _{i=1}^{n}{\hat{\eta }}_{i}^{2}$, where ${\hat{\eta }}_{i}=-\int _{0}^{\tau }{\hat{S}}(u){\hat{\phi }}_{i}(u)du$.

We now provide a set of results pertinent to the asymptotic properties list in Sect. 3.2 for semiparametric model. The assumed model for unbiased death time hazard is given by

$$\begin{aligned} \lambda (t|X)=\lambda _{0}(t)\exp (\beta _{0}^{T}X). \end{aligned}$$

Correspondingly, the cumulative hazard satisfies

$$\begin{aligned} \varLambda (t|X)=\varLambda _{0}(t)\exp (\beta _{0}^{T}X). \end{aligned}$$

We abbreviate $\varLambda (t|X)$ as $\varLambda _{X}(t)$ and its estimator is ${\hat{\varLambda }}_{X}(t)$. The subscript X is used for differentiating semiparametric model given covariates from nonparametric model.

Lemma 3

Under the regularity assumptions (a) (b) (c) and (d) given above, when $n\rightarrow \infty$, for $0<t<\tau ^{*}$, the random process ${\hat{\varLambda }}_{X}(t)-\varLambda _{X}(t)$ converges to a zero-mean Gaussian process with variance–covariance function $\sigma _{\varLambda _{X}}(t_{1},t_{2})=E\{\psi _{1}(t_{1})\psi _{1}(t_{2})\}$.

Proof of Lemma 3

Firstly, we make the following decomposition:

$$\begin{aligned} \sqrt{n}\{{\hat{\varLambda }}_{X}(t)-\varLambda _{X}(t)\}=\sqrt{n}\{{\hat{\varLambda }}_{X}(t,{\hat{\beta }})-{\hat{\varLambda }}_{X}(t,\beta _{0})\} +\sqrt{n}\{{\hat{\varLambda }}_{X}(t,\beta _{0})-\varLambda _{X}(t)\} \end{aligned}$$

Through a Taylor series expansion of ${\hat{\varLambda }}_{X}(t,{\hat{\beta }})$ around $\beta _{0}$, it is straightforward to show that the first item can be derived as

$$\begin{aligned}&\sqrt{n}\{{\hat{\varLambda }}_{X}(t,{\hat{\beta }})-{\hat{\varLambda }}_{X}(t,\beta _{0})\}\nonumber \\&\quad =\int _{0}^{t}\left\{ X-\frac{{\mathcal {S}}^{(1)}(u,\beta _{0})}{{\mathcal {S}}^{(0)}(u,\beta _{0})}\right\} ^{\text {T}}\text {d}\varLambda _{X}(u,\beta _{0}) \sqrt{n}({\hat{\beta }}-\beta _{0})+o_{P}(1), \end{aligned}$$

where ${\mathcal {S}}^{k}(t,\beta )=\frac{1}{n}\sum _{i=1}^{n}X_{i}^{\bigotimes k}\exp (\beta 'X_{i})R_{i}(t)$. And ${\mathcal {S}}^{k}(t,\beta )$ converges to its expectation $s^{k}(t,\beta )$ in probability.

$U(\beta )$ can be reexpressed as

$$\begin{aligned} U(\beta )=\frac{1}{n}\sum _{i=1}^{n}\int _{0}^{\tau ^{*}}\{X_{i}-\frac{S^{(1)}(u,\beta )}{S^{(0)}(u,\beta )}\}dN_{i}(u). \end{aligned}$$

Under the regularity condition (c) and (d), it shows from Huang and Qin (2012) that $\sup _{\beta \in {\mathcal {B}}}|U(\beta )-{\tilde{U}}(\beta )|\rightarrow 0$ almost surely as $n\rightarrow \infty$, with

$$\begin{aligned} {\tilde{U}}(\beta )=E\{X_{1}N_{1}(\tau ^{*})\}-\int _{0}^{\tau ^{*}}\frac{s^{(1)}(u,\beta )}{s^{(0)}(u,\beta )}dW(u). \end{aligned}$$

Define $\varGamma (\beta )=dU(\beta )/d\beta$ and ${\tilde{\varGamma }}(\beta )=d{\tilde{U}}/d\beta$, that is,

$$\begin{aligned} \varGamma (\beta )=\int _{0}^{\tau ^{*}}[-\frac{S^{(2)}(u,\beta )}{S^{(0)}(u,\beta )}+\{\frac{S^{(1)}(u,\beta )}{S^{(0)}(u,\beta )}\}^{\otimes 2}]\{ \frac{1}{n}\sum _{i=1}^{n}dN_{i}(u)\} \end{aligned}$$

and

$$\begin{aligned} {\tilde{\varGamma }}(\beta )=\int _{0}^{\tau ^{*}}[-\frac{s^{(2)}(u,\beta )}{s^{(0)}(u,\beta )}+\{\frac{s^{(1)}(u,\beta )}{s^{(0)}(u,\beta )}\}^{\otimes 2}]dW(u). \end{aligned}$$

Applying the Taylor series expansion, it can be derived as ${\hat{\beta }}-\beta _{0}=\varGamma ^{-1}(\beta ^{*}) (U({\hat{\beta }})-U(\beta _{0}))$, where $\beta ^{*}$ lies between ${\hat{\beta }}$ and $\beta _{0}$. According to Huang and Qin (2012), ${\hat{\beta }}$ converges in probability to $\beta _{0}$ and $\sup _{\beta \in {\mathcal {B}}}|\varGamma (\beta )-{\tilde{\varGamma }}(\beta )|\rightarrow 0$. Thus, ${\hat{\beta }}-\beta _{0}=-{\tilde{\varGamma }}^{-1}(\beta _{0})U(\beta _{0}).$

Define $M_{i}(t,\beta )=N_{i}(t)-\int _{0}^{t}\exp (\beta 'X_{i})R_{i}(u)d\varLambda _{0}(u)$ and applying the functional delta method (Andersen et al. 2012), $U(\beta )$ can be derived as $n^{-1}\sum _{i=1}^{n}\xi _{i}(\beta )+o_{p}(n^{-1/2})$ uniformly on $t\in [0,\tau ^*]$, with

$$\begin{aligned} \xi _{i}(\beta )=\int _{0}^{\tau ^{*}}\{X_{i}-\frac{s^{(1)}(u,\beta )}{s^{(0)}(u,\beta )} \}dM_{i}(u,\beta ). \end{aligned}$$

Then, the second item can be derived as

$$\begin{aligned} \sqrt{n}\{{\hat{\varLambda }}_{X}(t,\beta _{0})-\varLambda _{X}(t)\}&=\exp (\beta _{0}'X)n^{-\frac{1}{2}}\sum _{i=1}^{n}\int _{0}^{t}\frac{\text {d}M_{i}(u,\beta _{0})}{{\mathcal {S}}^{(0)}(u,\beta _{0})}\\&=\exp (\beta _{0}'X)n^{-\frac{1}{2}}\sum _{i=1}^{n}\int _{0}^{t}\frac{\text {d}M_{i}(u,\beta _{0})}{s^{(0)}(u,\beta _{0})}+o_{p}(1) \end{aligned}$$

Finally, it is easy to show that

$$\begin{aligned} {\hat{\varLambda }}_{X}(t)-\varLambda _{X}(t)=n^{-\frac{1}{2}}\sum _{i=1}^{n}\psi _{i}(t)+o_{P}(1), \end{aligned}$$

where

$$\begin{aligned} \psi _{i}(t)= & {} -\int _{0}^{t}\{X-\frac{s^{(1)}(u,\beta _{0})}{s^{(0)}(u,\beta _{0})}\}^{\text {T}}\text {d}\varLambda _{X}(u,\beta _{0}) {\tilde{\varGamma }}^{-1}(\beta _{0})\xi _{i}(\beta _{0})\\&+\exp (\beta _{0}'X)\int _{0}^{t}\frac{\text {d}M_{i}(u,\beta _{0})}{s^{0}(u,\beta _{0})}. \end{aligned}$$

Write

$$\begin{aligned} \kappa _{i}(t)=-\int _{0}^{t}\{X-\frac{s^{(1)}(u,\beta _{0})}{s^{(0)}(u,\beta _{0})}\}^{\text {T}}\text {d}\varLambda _{X}(u,\beta _{0}) {\tilde{\varGamma }}^{-1}(\beta _{0})\xi _{i}(\beta _{0}). \end{aligned}$$

Since $\kappa _{i}(t)$ is a monotone function increasing with t and $E\kappa _{i}(t)=0$, the weak convergence of $n^{-1/2}\sum _{i=1}^{n}\kappa _{i}(t)$ on $(0,\tau ^{*}]$ can be easily shown by using theorem 2.7.5 in Van Der Vaart and Wellner (1996).

Similarly, by the Lemma 2.6.18 of Van Der Vaart and Wellner (1996), $\{\exp (\beta _{0}'X)\int _{0}^{t}\frac{\text {d}M_{i}(u,\beta _{0})}{s^{0}(u,\beta _{0})}, t\in [0, \tau ^{*}], \beta \in {\mathcal {B}}\}$ is a Donsker class, Lemma 3 is easily proved. $\square$

Lemma 4

Under the regularity assumptions (a) (b) (c) and (d), $\sup \limits _{0<t\le \tau ^{*}} |{\hat{\varLambda }}_{X}(t)-\varLambda _{X}(t)|$ converges to 0 in probability, when $n\rightarrow \infty$.

Proof of Lemma 4

Since every Donsker class is a Glivenko-Cantelli class, we can prove Lemma 4 easily with the result of Lemma 3. $\square$

Proof of Theorem  2

Let $S_{X}(t)$ denote the true survival function of ${\tilde{T}}$, conditional on the covariates. Its corresponding estimator proposed in our article is ${\hat{S}}_{X}(t)$. According to the proof of Theorem 1, similarly, $\sqrt{n}({\hat{\mu }}_{\tau |X}-\mu _{\tau |X})$ can be written as

$$\begin{aligned} \sqrt{n}({\hat{\mu }}_{\tau |X}-\mu _{\tau |X})= & {} \sqrt{n}\int _{0}^{\tau }{\hat{S}}_{X}(u)-S_{X}(u)du\\= & {} \sqrt{n}\int _{0}^{\tau }e^{-{\hat{\varLambda }}_{X}(u)}-e^{-\varLambda _{X}(u)}du\\= & {} -\sqrt{n}\int _{0}^{\tau }S_{X}(u)({\hat{\varLambda }}_{X}(u)-\varLambda _{X}(u))du+o_{p}(1)\\= & {} n^{-\frac{1}{2}}\sum _{i=1}^{n}\varphi _{i}(\tau )+o_{p}(1), \end{aligned}$$

uniformly $\tau \in [0,\tau ^{*}]$, where $\varphi _{i}(\tau )=-\int _{0}^{\tau }S_{X}(u)\psi _{i}(u)du$.

Combined with Lemmas 3 and 4, the weak convergence of $n^{1/2}({\hat{\mu }}_{\tau |X}-\mu _{\tau |X})$ can be proved with continuous mapping theorem. Since the $\varphi _{i}$ variates are independent and identically distributed with mean 0, it is easy to get that ${\hat{\mu }}_{\tau |X}$ converges to $\mu _{\tau |X}$ in probability and $n^{1/2}({\hat{\mu }}_{\tau |X}-\mu _{\tau |X})$ converges weakly to a Gaussian process with mean 0 and covariance $E(\varphi _{i}(t)\varphi _{i}(s))$ for $t,s \in (0,\tau ^*)$. $\square$

Proof of Theorem 3

Under the assumption that the two observed samples are independent, it is obvious that $\sqrt{n}\{{\hat{\mu }}_{\tau ,1}-\mu _{\tau ,1}\}$ and $\sqrt{n}\{{\hat{\mu }}_{\tau ,2}-\mu _{\tau ,2}\}$ are independent. Since

$$\begin{aligned} \sqrt{n}({\hat{d}}_{\tau }-d_{\tau })=\sqrt{n}\{{\hat{\mu }}_{\tau ,1}-\mu _{\tau ,1}\}-\sqrt{n}\{{\hat{\mu }}_{\tau ,2}-\mu _{\tau ,2}\}, \end{aligned}$$

the asymptotic normality of $\sqrt{n}({\hat{d}}_{\tau }-d_{\tau })$ can be derived from the asymptotic normality of $\sqrt{n}\{{\hat{\mu }}_{\tau ,1}-\mu _{\tau ,1}\}$ and $\sqrt{n}\{{\hat{\mu }}_{\tau ,2}-\mu _{\tau ,2}\}$ which is apparent under Corollary 1. $\square$

Proof of Theorem 4

Since

$$\begin{aligned}&\sqrt{n}\{{\hat{r}}_{\tau }-r_{\tau }\}=\sqrt{n}\left\{ \frac{{\hat{\mu }}_{\tau ,1}}{{\hat{\mu }}_{\tau ,2}}-\frac{\mu _{\tau ,1}}{\mu _{\tau ,2}}\right\} \\&\quad =\sqrt{n}\left\{ \frac{{\hat{\mu }}_{\tau ,1}}{{\hat{\mu }}_{\tau ,2}}-\frac{\mu _{\tau ,1}}{{\hat{\mu }}_{\tau ,2}}+ \frac{\mu _{\tau ,1}}{{\hat{\mu }}_{\tau ,2}}-\frac{\mu _{\tau ,1}}{\mu _{\tau ,2}}\right\} \\&\quad =\frac{1}{{\hat{\mu }}_{\tau ,2}}\{\sqrt{n}({\hat{\mu }}_{\tau ,1}-\mu _{\tau ,1})-r_{\tau }\sqrt{n}({\hat{\mu }}_{\tau ,2}-\mu _{\tau ,2})\}, \end{aligned}$$

based on Corollary 1, the asymptotic normality of $\sqrt{n}({\hat{r}}_{\tau }-r_{\tau })$ can be derived from the asymptotic normality of $\sqrt{n}\{{\hat{\mu }}_{\tau ,1}-\mu _{\tau ,1}\}$ and $\sqrt{n}\{{\hat{\mu }}_{\tau ,2}-\mu _{\tau ,2}\}$ under Slutsky Theorem. $\square$