Seismometer self-noise estimation using a single reference instrument

Abstract

A new method is presented for the self-noise estimation of a seismometer using a single, side-by-side, reference instrument and taking into consideration the misalignment in the orientation of both seismometers. The self-noise of seismometers is extracted directly from the measurements without using any information relating to the transfer functions. This procedure can be applied if the self-noise of the reference seismometer is well known and defined, or if the self-noise of the reference seismometer is sufficiently below the self-noise of the tested instrument and can be neglected. The latter case applies to this study. An algorithm is also developed where we apply self-noise data in order to determine the orientation misalignment between two seismometers, which is then resolved in three-dimensional space. This new method provides an estimate of the self-noise and can also be used to extract some parameters of the installed seismic system in comparison with the reference seismic system, such as generator constants and seismometer orientation or to eliminate unwanted noise sources, which have their origin in the seismic station’s design. The new technique was applied to the CMG-3ESPC and CMG-40T seismometers, where an STS-2 instrument served as the reference seismometer.

Appendix

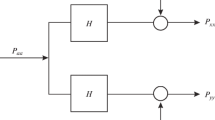
We have two three-component seismological systems, each consisting of a broadband seismometer and an analogue-to-digital converter (or an acquisition unit). The first is marked with the index ‘q’, and the second with the index ‘r’. We assume that the transfer functions for both systems are flat inside of their respective bandwidth, noise-independent, and the instrumental noise of the acquisition units is lower than that of the seismometers. Those axes in both seismological systems are not ideally perpendicular to each other (Fig. 7) and also their gains are not the same. The seismometers are not perfectly aligned with each other in the same direction, even if we try to do our best (Holcomb 2002). Because of misalignment errors the signals between the two seismological systems are not purely coherent (Holcomb 1990). To achieve coherency, the data from system ‘r’ need to be transformed into system ‘q’ to detect the same seismic signal. A matrix A represents such a transformation:

$$ {{\mathbf{x}}^q} = {\mathbf{A}}{{\mathbf{x}}^r} \to \left[ {\begin{array}{*{20}{c}} {x_{{1}}^q} \\ {x_{{2}}^{\text{q}}} \\ {x_{{3}}^{\text{q}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}{c}} {{a_{{11}}}} & {{a_{{12}}}} & {{a_{{13}}}} \\ {{a_{{21}}}} & {{a_{{22}}}} & {{a_{{23}}}} \\ {{a_{{31}}}} & {{a_{{32}}}} & {{a_{{33}}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}{c}} {x_{{1}}^{\text{r}}} \\ {x_{{2}}^{\text{r}}} \\ {x_{{3}}^{\text{r}}} \\ \end{array} } \right]. $$

(16)

Fig. 7

The sensors of the system ‘q’ lie on the axis of a coordinate system. Sensors in the system ‘r’ are not aligned equal to the system ‘q’

Usually, $\left| {\det ({\mathbf{A}})} \right| \ne 1$: the matrix A includes both rotation and a scaling factor (the ratio of the generator constants) of one seismometer with respect to the other. In the procedure where we use two seismic systems close to each other these matrices are not de facto known. To determine the parameters of the matrix A, the self-noise of the seismometers can be used. In a three-dimensional coordinate system the ‘i’-th sensor of system ‘q’ lies on the axis of the ‘i’-th coordinate system, where i = 1,2,3, (Fig. 7). With the direction ‘i’, the sensor ‘i’ of the seismic system ‘q’ detects the seismic signal ‘x _i’ and the instrumental noise ‘n_i’:

$$ y_{\text{i}}^{\text{q}} = {x_{\text{i}}} + n_{\text{i}}^{\text{q}}. $$

(17)

Similarly, the signal of the system ‘r’ in the direction ‘i’ is a linear combination of all three outputs:

$$ {\text{y}}_{\text{i}}^{\text{r}} = \sum\limits_{{{\text{j}} = 1}}^3 {{a_{\text{ij}}}\left( {x_{\text{j}}^{\text{r}} + n_{\text{j}}^{\text{r}}} \right)} = {x_{\text{i}}} + \sum\limits_{{{\text{j}} = 1}}^3 {{a_{\text{ij}}}n_{\text{j}}^{\text{r}}}, $$

(18)

where a _i1, a _i2, and a _i3 are the elements of the transformation matrix A for the component ‘i’ and $n_{\text{j}}^{\text{r}}$; j = 1,2,3 is the instrumental noise of the component ‘j’ of the seismic system ‘r’. The notations of Eqs. 17 and 18 in the frequency domain are:

$$ Y_{\text{i}}^{\text{q}} = {X_i} + N_{\text{i}}^{\text{q}}, $$

(19)

$$ Y_{\text{i}}^{\text{r}} = {X_{\text{i}}} + \sum\limits_{{{\text{j}} = 1}}^3 {{a_{\text{ij}}}N_{\text{j}}^{\text{r}}}, $$

(20)

where $Y_{\text{i}}^{\text{r}}$, $Y_{\text{i}}^{\text{q}}$, $X_{\text{i}}$, $N_{\text{i}}^{\text{r}}$ and $N_{\text{i}}^{\text{q}}$ represent the Fourier transforms of $y_{\text{i}}^{\text{r}}$, $y_{\text{i}}^{\text{q}}$, $x_{\text{i}}$, $n_{\text{i}}^{\text{r}}$ and $n_{\text{i}}^{\text{q}}$. We assume that the instrumental noise between the outputs of the seismic systems is uncorrelated and the self-noise and the input seismic signal x_i are also uncorrelated. Assuming that the system is linear and the outputs from both seismic systems in the direction ‘i’ can be written using the power spectral density:

$$ {{\text{P}}_{{{{\text{q}}_i}{{\text{q}}_i}}}} = Y_{\text{i}}^{\text{q}}Y_{\text{i}}^{{{\text{q*}}}} = {{\text{P}}_{{{x_i}{x_i}}}} + {{\text{N}}_{{{{\text{q}}_i}{{\text{q}}_i}}}}, $$

(21)

$$ {{\text{P}}_{{{{\text{r}}_i}{{\text{r}}_i}}}} = Y_{\text{i}}^{\text{r}}Y_{\text{i}}^{{{\text{r}}*}} = {{\text{P}}_{{{x_i}{x_i}}}} + \sum\limits_{{{\text{j}} = 1}}^3 {a_{\text{jj}}^2{{\text{N}}_{{{{\text{r}}_j}{{\text{r}}_j}}}}}, $$

(22)

where * denotes the complex conjugation. ${{\text{P}}_{{{x_i}{x_i}}}} = {X_i}X_i^{*}$ is the autopower spectrum (Sleeman et al. 2006) of the seismic input signal (ground motion) in the direction ‘i’ and ${{\text{N}}_{{{{\text{q}}_i}{{\text{q}}_i}}}} = N_{\text{i}}^{\text{q}}N_{\text{i}}^{{{\text{q*}}}}$ and ${{\text{N}}_{{{{\text{r}}_i}{{\text{r}}_i}}}} = N_{\text{i}}^{\text{r}}N_{\text{i}}^{{{\text{r}}*}}$ are the autopower spectra of the instrumental noise. The cross-power spectrum ${{\text{P}}_{{{{\text{r}}_i}{{\text{q}}_i}}}}$is simply:

$$ {{\text{P}}_{{{{\text{r}}_i}{{\text{q}}_i}}}} = {{\text{P}}_{{{x_i}{x_i}}}}. $$

(23)

Using Eqs. 21, 22 and 23 we can apply the “average” instrumental noise power spectra ${\overline {\text{N}}_{\text{ii}}}$ (Eq. 13) in the direction ‘i’ as a function of the frequency ‘v _p ’ and the parameters a _i1, a _i2 and a _i3 as:

$$ \begin{gathered} {\overline {\text{N}}_{{ii}}}\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_p}} \right) = \frac{1}2\left({{{{\text{P}}_{{{{\text{r}}_i}{{\text{r}}_i}}}}\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_p}} \right) + {{\text{P}}_{{{{\text{q}}_i}{{\text{q}}_i}}}}\left( {{\nu_p}} \right)}} \right)- \hfill \\ - \sqrt {{{{\text{P}}_{{{{\text{q}}_i}{{\text{r}}_i}}}}({a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_p}){{\text{P}}_{{{{\text{q}}_i}{{\text{r}}_i}}}}{{\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_p}} \right)}^{*}}}} . \hfill \\ \end{gathered} $$

(24)

To find the parameters a _i1, a _i2 and a _i3, by which the contribution of the ground motion ${{\text{P}}_{{{x_i}{x_i}}}}$ in the direction ‘i’ from both seismometers at the right-hand side of Eq. 24 are canceled out, is one of our aims. The values a _i1, a _i2 and a _i3 can be estimated by using non-linear least-squares data fitting and the Gauss–Newton method. Let us define the frequency v _p and the interval 2n around this frequency: [p−n, p + n]. The residual vector (Heath 2002) in the direction ‘i’ at this frequency interval is:

$$ {r_i}\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_{{p + l}}}} \right) = {\overline {\text{N}}_{\text{ii}}}\left( {{a_{{{\text{i}}1}}},{a_{{{\text{i}}2}}},{a_{{{\text{i}}3}}},{\nu_{{p + l}}}} \right) - S\left( {{\nu_{{p + l}}}} \right),\quad l = - n,...,n. $$

(25)

The function S(v) is a synthetic trace and represents the ideal instrumental noise. This function is usually not known. Instead of this, the synthetic trace can be formulated according to the lowest expected self-noise value. If the frequency interval is short enough, and if the self-noise is the lowest in this frequency band, zero values can be used instead. The initial guess for the initial parameters is set in the direction of the ideal orientation and the alignment of the reference seismometer, so the initial parameters are ${a_{{{1}1}}} = {a_{{{22}}}} = {a_{{{33}}}} = 1$ and 0 otherwise. Using the first approximate solution, a new approximate solution is computed based on local linearization around the current point using the Jacobian matrix of the residual vector. This process is repeated until convergence is achieved. When the residual obtains its minimum, the values of the parameters a _i1, a _i2 and a _i3 represent the optimal solution for the transformation matrix. The parameters are in good agreement with available observations. This approach is a power-based method and, theoretically, produces two possible estimates for each component, because the analysis does not retain the information about the phase (Holcomb 2002). But a close inspection of the evaluated results shows that the vast majority of the evaluated parameters are as expected. The reason is that the orientation of the reference seismometer is mostly known, the vertical component of the tested system is usually set similar to the reference system and the initial parameters are set with regard to the vertical component. When the parameters of the matrix A are determined, the seismic signal of the reference seismological system can be transformed into the seismic signal of the tested seismological system, without any a priori knowledge of the gain constant and of the rotation of the tested seismometer. This procedure can also be performed to define the orientation of the borehole seismometer with regard to the surface seismometer.

Figure 8 depicts the evaluated transformation matrices of a CMG-3ESPC seismometer (s/n T34238) and a STS-2 seismometer (s/n 80448) and the evaluated transformation matrices of a CMG-40T seismometer (s/n T4B19) and a STS-2 seismometer (s/n 80448). The seismometers were installed side by side. The calculated self-noises for both seismometers and for both models are depicted in Figs. 9 and 10, where the self-noise was calculated using Eq. 9 without any information about the reference system’s self-noise. The tests were performed at Conrad Laboratory, Austria. In both cases the input is a 12-h finite-length-time seismic-data segment, sampled at 200 samples per second. For the power spectral density estimation, Welch’s method is used, using a Matlab(C) built-in function, with a Hanning window of length 2¹⁶ and with 75% overlapping time-series segments. For both cases the transformation matrix for the 3D model was calculated in the frequency interval from 0.2 to 0.5 Hz.

Fig. 8

Evaluated transformation matrices used in our article for the 3D model, correlating the tested and the reference seismometer

Fig. 9

The estimated self-noise of the vertical component of a CMG-3ESPC seismometer (s/n T34238), using the 1D model (dotted line, marked N _{(1D model)}) and the 3D model (N _{(3D model)})

Fig. 10

The estimated self-noise of the vertical component of a CMG-40T seismometer (s/n T4B19), using the 1D model (N _{(1D model)}) and using the 3D model (N _{(3D model)})