Toward understanding the second universality—A journey inspired by Arthur Stanley Nowick

Abstract

In 1991, Arthur Stanley Nowick and his co-workers discovered a new universality, now known as nearly constant loss (NCL) or second universality. This mini-review, written in honor of A.S. Nowick, reports on the present authors’ more recent endeavors and advances on their way toward understanding the second-universality phenomenon. In pursuit of that goal, new ideas and new data have led us to new questions and new answers. The essence of the new ideas was to consider time-dependent single-particle potentials, caused by Coulomb interactions and experienced by locally mobile ions. The dynamics of such ions were described in terms of a rate equation, and model conductivity spectra showing the NCL effect could be derived from it, with the help of linear response theory. New data corroborated the predictions made by the model. Also, our experimental data suggested a gradual transition, occurring with decreasing temperature, from a slightly activated NCL-type behavior to the non-activated features of the second universality. Two new questions have emerged. (i) Is it possible to quantify the transition mentioned above? (ii) Is there a crossover of the low-temperature, second-universality ionic conductivity from its characteristic linear frequency dependence to a quadratic one at low frequencies? New answers to our two questions can now be given, both of them in the affirmative. In particular, the crossover in the frequency dependence has been identified as an implication of the localization of the non-activated ionic motion.

1 Introduction

It was Arthur Stanley Nowick who inspired all of us to take a journey toward understanding the new universality, also known as nearly constant loss (NCL) or second universality, which he and his co-workers had discovered in 1991 [1]. The present mini-review, written in his honor, is meant to give a brief account of our results obtained on that journey during the past 12 years.

We would like to start this report by recording a memorable visit paid by two of us (K.F. and H.J.) to Arthur S. Nowick in his office at Columbia University, New York, on November 9, 2000. In the late 1990s, the shapes of frequency-dependent conductivities due to the activated hopping motion of mobile ions in disordered solid electrolytes had been carefully reconsidered [2–4]. In particular, it had become evident that those ‘universal’ master curves that were obtained from them by time-temperature superposition [4–7] generally displayed a characteristic deviation from the power-law description suggested earlier by A.K. Jonscher [8, 9]. The ‘universal’ shape observed in a double logarithmic plot of scaled conductivity versus scaled angular frequency, see Fig. 1, was, instead, well described in terms of a non-constant slope which kept increasing, slowly approaching the value of one in the limit of high values of ln(ω/ω₀) [2–4].

Fig. 1

First universality. This scaled representation of experimental conductivities (circles: data from 0.45 LiBr ⋅ 0.56 Li₂O ⋅ B₂O₃ glass [10, 11]) is characteristic of many disordered ion conductors which broadly differ in phase, structure and composition. The solid line is obtained from our model, see below

With this result in mind, K.F. tried to convince A.S. Nowick that his new universality [1], with a slope of one in a representation like Fig. 1, could be regarded as that part of the known ‘universal’ master curve, which is observed at high values of ln(ω/ω₀) and should become visible in the accessible frequency range once the experimental temperatures were sufficiently low.

Arthur Nowick immediately detected the fallacy in the argument. He unerringly emphasized the fact that his new universality, cf. Fig. 2, did not show any measurable temperature dependence even in the cryogenic temperature regime. It must, therefore, be caused by ionic movements which required no thermal activation at all, thus being completely different from the activated hopping processes that caused the ‘universal’ behavior seen at higher temperatures. This was, indeed, totally irrefutable and utterly convincing. It should, however, be mentioned that it took us several years’ time to arrive at a self-consistent view of the non-activated ion dynamics, both experimentally and by modeling.

Fig. 2

Second universality (nearly constant loss). Low-temperature conductivity isotherms displaying a linear frequency dependence and essentially no temperature dependence (data from 0.3 Na₂O ⋅ 0.7 B₂O₃ glass [12, 13]). The term nearly constant loss (NCL) refers to the dielectric loss function, ε ′ ′ ∝ σ(ν)/ν, which is independent or nearly independent of both frequency and temperature

In retrospect, the résumé of our visit is as follows. What we owe to Arthur Nowick is the insight that there are, indeed, two universalities. One of them, now called the first universality, see Fig. 1, is due to activated hopping processes of ions along passageways formed by interconnected sites; at sufficiently high temperatures, this behavior is quite generally observed in disordered solid electrolytes. The other one, now called the second universality, see Fig. 2, is caused by non-activated ionic movements, which must remain strictly localized; it is observed at sufficiently low temperatures and appears to be ubiquitous in disordered ionic materials.

2 Separating the two universalities from each other

While the characteristic features of the first and second universalities, see Figs. 1 and 2, are easily identified at high and low temperatures, respectively, they appear to be superimposed at intermediate temperatures. An example is given in Fig. 3 [13, 14].

Fig. 3

Log-log plot of the frequency-dependent conductivity of 0.3 Na₂O ⋅ 0.7 B₂O₃ glass at different temperatures [13, 14]. The filled symbols mark the transition from the first to the second universality at three different frequencies. For the identification of these points, see Fig. 4

Many conductivity isotherms, taken on 0.3 Na₂O · 0.7 B₂O₃ glass between 0.1 Hz and 1 MHz, are shown in the figure. The limiting cases, corresponding to Figs. 1 and 2, are clearly seen above 325 K and below 125 K, respectively. It appears, however, impossible to define crossover points, from the first universality to the second, merely by inspection. Nevertheless, such points can be determined, cf. the three points highlighted in Fig. 3. This has been achieved with the help of a different representation, which is given in Fig. 4.

Fig. 4

Iso-frequency representation of log σ versus 1/T for 0.3 Na₂O ⋅ 0.7 B₂O₃ glass [13, 15]. The dash-dotted lines indicate the Arrhenius temperature dependence of σ _DC and σ _HF . The filled diamonds represent the crossover from the first to the second universality

Figure 4 is a logarithmic plot of conductivity versus inverse temperature, σ(1/T), again with data from 0.3 Na₂O · 0.7 B₂O₃ glass, but now taken at three fixed frequencies [13, 15]. At large values of 1/T, the conductivity is virtually independent of temperature and directly proportional to frequency, thus displaying the characteristics of the second universality. On the other hand, the first universality dominates at low inverse temperatures, the fixed-frequency conductivity strongly increasing with decreasing 1/T.

While the defining features of the second universality are quite obvious in Fig. 4, a similarly unique identification of the first universality requires a reliable, quantitative representation of its dependence on both temperature and frequency. A suitable model description has been provided by the MIGRATION concept, see below, and the solid lines that reproduce the iso-frequency data of Fig. 4 at high temperatures have been obtained from it. On the basis of these solid lines, as well as the dashed lines representing the second universality, the crossover points have been chosen to be those, where the contributions of the two components are equal. Note that these are the points that have been included in Fig. 3. For further details concerning Fig. 4, see Ref. [13].

The MIGRATION concept is the most recent version of a series of models which describe the dynamics of jump relaxation in terms of coupled rate equations [13, 16–20]. The acronym ‘MIGRATION’, for MIsmatch Generated Relaxation for the Accommodation and Transport of IONs, is meant to express the essence of the model treatment, while the leitmotif of Fig. 5 is meant to serve for an easy visualization of the time-dependent processes involved [13].

Fig. 5

Schematic representation of the leitmotif of the MIGRATION concept [13]. The backward hop of the ion signifies the possible relaxation along the single-particle route, while the shift of the caged potential indicates the possible relaxation along the many-particle route. The effective potential experienced by the ion is sketched by the solid line

As suggested by the acronym, each elementary hop of an ion is supposed to create mismatch with respect to the momentary arrangement of its mobile neighbors. As a consequence, the system will search for ways to reduce this mismatch, which is possible on two competing routes. These are (i) the single-particle route, with the ion hopping backwards, and (ii) the many-particle route, with the surrounding ions rearranging. Relaxation on the many-particle route causes accommodation of the ion at its new site, thus successfully completing an individual step of ionic transport, which contributes to the DC conductivity. On the other hand, relaxation on the single-particle route results in the observed frequency dependence of the conductivity, σ(ω). Typically, the limiting value of σ(ω) at high frequencies, σ _HF , is much larger than the one at low frequencies, σ _DC , indicating that there are many more ‘elementary’ hops than ‘successful’ ones and that, in other words, correlated forward-backward hopping sequences must be considered a typical feature of the ion dynamics.

In the model, the time dependence of the competing processes (i) and (ii) is described by three coupled equations which can be solved for the time-dependent correlation factor, W(t). This function is defined as the time derivative of the mean square displacement of the mobile ions, $\left\langle {r}^2(t)\right\rangle$, normalized by W(0) = 1. The time derivative of W(t) is then proportional to the velocity autocorrelation function, $\left\langle \underset{\bar{\mkern6mu}}{\upsilon }(0)\cdot \underset{\bar{\mkern6mu}}{\upsilon }(t)\right\rangle$, while the frequency-dependent conductivity itself, σ(ω), is in a good approximation proportional to the Fourier transform of $\left\langle \underset{\bar{\mkern6mu}}{\upsilon }(0)\cdot \underset{\bar{\mkern6mu}}{\upsilon }(t)\right\rangle$ [13, 20]. This procedure, which is based on linear response theory [21], thus takes us from W(t) to σ(ω). The proper temperature dependence of σ(ω, T) is obtained, once the rates of ‘elementary’ and ‘successful’ hops (and hence σ _HF and σ _DC ) are both regarded as Arrhenius activated.

As has been documented for many disordered solid electrolytes [11, 13, 20], experimental data of ionic conductivities due to hopping processes, including their dependence on both frequency and temperature, are generally well reproduced by the MIGRATION concept. This includes in particular the master curve presented in Fig. 1, i.e. the solid line that perfectly fits the experimental data. In the context of our present endeavor to gain an understanding of the second universality, the MIGRATION concept is used to identify that part of the conductivity which is due to activated ionic hopping, as in the example of Fig. 4. As a rule, a reliable removal of first-universality contributions from total conductivities is imperative for isolating and investigating the features of the second universality.

3 Second universality: new ideas, new data, new questions

There has always been a broad consensus that the second universality is a fingerprint of a collective phenomenon, with a large number of ions moving locally in a cooperative fashion.

In early interpretations, static distributions of asymmetric double-well potentials (ADWPs) were assumed to exist for the locally mobile ions, providing a wide range of relaxation times. Indeed, the ADWP model has often been used to fit experimental data [22–24]. In order to visualize the collective nature of the underlying ion dynamics, one of us (H.J.) coined the term ‘jellyfish’ effect [24].

A new idea was introduced in 1998, when W. Dieterich et al. used Monte Carlo simulations to study random distributions of reorienting and interacting electric dipoles [25–27]. The conductivity spectra thus obtained displayed a linear, NCL-type regime that was situated between two crossover points, with σ(ω) ∝ ω ² and σ(ω) = const. at lower and higher frequencies, respectively. With decreasing temperature, implying an increasing ratio of Coulomb energy by thermal energy, the NCL regime was found to span an increasing range in frequency, thus approaching the features of the second universality.

The essence of the new idea behind the Monte Carlo simulations was to abandon the static distributions of the ADWP model and to replace them by variations of local potentials in time, caused by Coulomb interactions and experienced by each reorienting dipole or locally mobile ion.

The same idea was used later, when a simple rate equation was formulated, which resulted in exactly the same shape of σ(ω) as obtained by the Monte Carlo simulations, see Fig. 6c [13, 14, 18, 28]. This rate equation was

Fig. 6

a An ion hops between the sites of a symmetric double-well potential. Interactions with other ions are not considered. b As in (a), but with Coulomb interactions included. c The frequency-dependent conductivity, resulting from the situation sketched in (b), is given by the curved line. The straight lines are guides to the eye

$$ -\kern0.4em \frac{d{W}_{LOC}(t)/ dt}{W_{LOC}(t)}={\omega}_1+{\omega}_2\cdot {W}_{LOC}(t). $$

(1)

The two angular frequencies, ω ₁ and ω ₂, were considered fixed at any given temperature, and the time-dependent function, W _LOC (t), denoted the normalized time derivative of the mean square displacement of locally mobile ions that were confined in double-well potentials, as in Fig. 6b. Obviously, such a locally mobile ion is equivalent to a reorienting dipole.

The rate equation (1) may be derived in two steps. In the first, the Coulomb interaction is still neglected, and the double-well potential is taken as symmetrical and time-independent, as in Fig. 6a. If the ion is at the right position at time t = 0 and is allowed to change positions later, then W _LOC (t) will be the time-dependent difference between the probabilities of finding it at the right and at the left [13, 20]. Evidently, this function must decay from W _LOC (0) = 1 to W _LOC (∞) = 0. Introducing a Debye-type rate of the decay, ω ₁, by equating W _LOC (t) = W _Debye (t) = exp(−ω ₁ t), one arrives at

$$ -\kern0.4em \frac{d{W}_{Debye}(t)/ dt}{W_{Debye}(t)}={\omega}_1. $$

(2)

Fourier transforming the time derivative of W _Debye (t) leads to the well-known Debye-type shape of the frequency-dependent conductivity, which is proportional to ω ²/(ω ² + ω ²₁ ) and does, of course, not contain any linear, NCL-type regime at intermediate frequencies.

In a second step, Coulomb interaction is introduced. The potential now becomes time-dependent, implying a time dependence of the hopping rate, as illustrated in Fig. 6b. Imagine that the “central” ion arrives in the potential minimum on the right-hand side at time t = 0. Then the other ions have reacted to the dipole field exerted by the ion while staying on the left. This means that they have arranged accordingly, lowering the potential on the left and increasing it on the right. Once the “central” ion has arrived on the right, it thus experiences a back-hop barrier that is smaller than in the Debye case. Its tendency to hop backwards is now increased, and on the right-hand side of Eq. (2) ω ₁ has to be replaced by some larger value, ω ₁ + ω ₂. However, the advantage for backward hopping will decay with time, while the neighboring ions are readjusting their arrangement. This decay is again governed by the time-dependent function W _LOC (t) [13, 20], leading to ω ₁ + ω ₂ ⋅ W _LOC (t) on the right-hand side of Eq. (2) and, therefore, to Eq. (1). The solution of Eq. (1) is

$$ {W}_{LOC}(t)=\frac{\omega_1}{\left({\omega}_1+{\omega}_2\right)\cdot \exp \left({\omega}_1t\right)-{\omega}_2}. $$

(3)

The resulting frequency-dependent conductivity does, indeed, display the same features as the one obtained by Dieterich et al., with a linear, NCL-type regime between two crossover angular frequencies, which are now identified as ω ₁ and ω ₂, respectively.

On the basis of the above modeling, the width of the NCL-type frequency regime should increase with decreasing temperature, which has meanwhile been verified and will be discussed below. In the case of the ‘pure’ second universality as presented in Fig. 2, both crossover angular frequencies are clearly outside the accessible frequency window. At higher temperatures, however, examples have been found where ω ₂ could be located in the microwave frequency regime, whereas the crossover at ω ₁ was swamped by the first-universality-type conductivity [12, 18, 20, 29].

New insights have been provided by new experimental conductivity data that do, indeed, display both crossover angular frequencies, including their temperature dependences [14]. By chance, all these features have been detected in a disordered ionic material that does not exhibit any measurable DC conductivity, i.e. in nominally pure amorphous boron oxide. Amorphous B₂O₃ inevitably contains traces of water, and the locally mobile charge carriers are supposed to be hydrogen ions, switching from one neighboring oxygen ion to another [14].

Figure 7 is a logarithmic plot of measured conductivities versus temperature, with data taken at three fixed frequencies. On the other hand, Fig. 8 shows the frequency dependence of the 185 K conductivity isotherm as well as its variations with decreasing temperature [13, 14]. A model line obtained on the basis of Eq. (3) is included in Fig. 8. At the crossover points, the change of slope is found to be more gradual in the experimental data than in the model curve. However, in view of the structural and dynamic heterogeneities in the amorphous solid, this is not unexpected.

Fig. 7

Temperature-dependent conductivity data sets of nominally pure amorphous boron oxide at three different frequencies. The maxima shift to higher temperatures as frequency is increased

Fig. 8

Frequency-dependent conductivity of nominally pure amorphous boron oxide at 185 K along with a model curve based on Eq. (3). The arrows indicate changes observed in the spectrum as temperature is decreased. The lengths of the arrows correspond to the respective rates of change. The two dots indicate the crossover points at ν ₁ = ω ₁/2π and ν ₂ = ω ₂/2π, cf. Fig. 6c

In contrast to the conductivities shown in Fig. 2, the iso-frequency data of Fig. 7 display a pronounced temperature dependence. On closer inspection it becomes obvious that the increasing and decreasing flanks of the σ(T) curves result from the temperature dependences of ω ₂ and ω ₁, respectively, as indicated in Fig. 8. In particular, the ‘two-to-one’ crossover point is seen to move rapidly to the lower left as temperature is reduced, the activation energy for ω ₁ being (0.36 ± 0.03) eV. At the same time, the linear, NCL-type part of the spectrum moves toward the lower right, indicating that the temperature dependence of the high-frequency conductivity is more pronounced than that of ω ₂. However, with ω ₁ decreasing much faster than ω ₂, the NCL part of the spectrum is not only seen to move to the lower right, but also to become more and more extended, suggesting that the defining features of the second universality, as in Fig. 2, may be attained at still lower temperatures.

Subsequently, in search of a disordered solid electrolyte that might show a similar transition toward the second universality in a more easily accessible conductivity range, we looked for systems with higher number densities of locally mobile ions. This led us to AgI⋅AgPO₃ glass which, upon cooling, did indeed display the expected development of the characteristics of the second universality [30, 31].

In this silver-ion conducting glass, the broadband non-vibrational conductivity spectrum, measured at 293 K, see Fig. 9, clearly exhibits a linear, NCL-type component at microwave frequencies. This component is superimposed onto the high-frequency part of a first-universality-type spectrum. The weight of the NCL-type feature suggests that the rapid localized motion must be ubiquitous in the glass. While the first crossover, at ν ₁ = ω ₁/2π, is swamped by the MIGRATION-type contribution, the second, at ν ₂ = ω ₂/2π, is visible in the millimeter to sub-millimeter wave regime [30].

Fig. 9

Conductivity spectra of AgI⋅AgPO₃ glass. The spectrum taken at 293 K displays the features of the first universality up to about 10 GHz, while a linear, NCL-type behavior is seen to dominate at higher frequencies. The 30 K and 20 K spectra show the characteristics of the second universality, and the dotted line indicates where its HF plateau is expected to lie

As in nominally pure amorphous boron oxide, the NCL-type, linear part of the spectrum is found to move to the lower right as temperature is reduced. At the same time, the thermally activated first-universality-type component becomes smaller and smaller, eventually falling outside the conductivity range of the figure. Most notably, however, the shifting of the NCL-type line comes to a halt, once the transition to the second universality is completed. Indeed, the linear conductivity, σ(ν) ∝ ν, becomes independent of temperature around and below 30 K, see Fig. 9 [31].

Obviously, the processes that ‘survive’ at low temperatures are those that require no activation, while the thermally activated ones have all ‘died out’.

Processes of either kind are best visualized in terms of the shapes of the time-dependent potentials felt by the locally mobile ions, cf. Fig. 10. Here, the upper panel corresponds to a forward-backward motion over a small barrier, as already discussed in Fig. 6b. On the other hand, a localized forward-backward motion that does not require any activation is sketched in the lower panel. In both cases, the time dependence of the potential bears resemblance to a see-saw [12–14]. The potential seen by the ion itself, while it moves in the course of time, is flat between neighboring positions in the lower panel, while the ion has to surmount a small barrier in the case of the upper one.

Fig. 10

The above “snapshots” of single-particle potentials are meant to represent instants of time at which the locally mobile ion is at its right or left point of return. The lower panel shows the basic low-temperature see-saw-type process of the second universality, in which the ion does not encounter any potential barrier. Activated processes, as shown in the upper panel, also contribute to the NCL-type conductivity at higher temperatures

Two sets of new questions have emerged from the data of Fig. 9.

• (i) How do contributions to the NCL-type conductivity that are due to localized, but slightly activated ionic movements develop with increasing temperature? More specifically, can a distribution of barrier heights, f(δ), be deduced from such data?

• (ii) In the second-universality low-temperature regime, is there a transition from the observed linear σ(ν) ∝ ν behavior to a quadratic σ(ν) ∝ ν ² behavior at lower frequencies? Can such a crossover be detected experimentally? Can arguments be found in favor of its existence?

Answers to these non-trivial questions will be given in the two following sections.

4 Detecting and describing strictly localized, but slightly activated processes

The NCL-type conductivity component observed in AgI⋅AgPO₃ glass at room temperature, above 10 GHz, cf. Fig. 9, is obviously not caused by the translational hopping motion of the mobile ions, but rather by localized and slightly activated ionic movements that are ubiquitous in the glassy network. By contrast, the second-universality effect seen in the same glass at low temperatures and low frequencies must be due to localized ionic movements that are not activated at all. Both effects involve many ions moving in single-particle potentials like those in Fig. 10, their see-saw-type time dependence being created by the Coulomb interaction.

It is tempting to ask whether, as temperature is increased from, say, 30 K upwards, it is possible to observe the gradual appearance of those additional localized processes which are characterized by a slight thermal activation and are, therefore, expected to contribute to the conductivity at elevated temperatures. Will these contributions be discernible before they are swamped by those that are caused by the translational hopping motion of the ions? This conjecture is examined in this section.

In Fig. 2 we have seen that 0.3 Na₂O · 0.7 B₂O₃ glass does not show any deviation from pure second-universality behavior below 75 K. In the temperature range between 100 K and 125 K, however, see Fig. 4, the conductivity data of this glass are found to deviate slightly from this behavior, i.e. from the dashed horizontal lines, particularly so at low frequencies. It is clear from Fig. 4 that this deviation occurs before translational hops are activated, and should, therefore, be a signature of activated, localized motion [13, 15].

In the following metaphosphate glasses, x AgI · (1-x) AgPO₃ (x = 0.05, 0.5), 0.05 AgX · 0.95 AgPO₃ (X = Br, Cl) and YPO₃ (Y = Ag, Na, Li), systematic conductivity measurements have been performed over wide ranges of temperature and frequency, spanning 5 K to 300 K and 10⁻¹ Hz to 10⁶ Hz, respectively [31]. As revealed by our results, localized but slightly activated processes are indeed a prominent feature in all of these glasses. Remarkably, the conductivities of the three YPO₃ glasses at any given frequency are very similar in magnitude and in their temperature dependence up to 150 K, see Fig. 11. The same is true for the three systems 0.05 AgX · 0.95 AgPO₃ (X = I, Br, Cl). In the two glasses x AgI · (1-x) AgPO₃ (x = 0, 0.05), there is virtually no difference in shape and magnitude of the conductivities up to 150 K. Note that the conductivities of our metaphosphate glasses, even at the lowest temperatures, are much higher than the lowest ones in Figs. 2 and 3.¹

Fig. 11

Temperature-dependent ionic conductivities of the metaphosphate glasses AgPO₃, LiPO₃, NaPO₃, measured at 3.4 kHz. The experimental uncertainty is smaller than the size of the symbols

In Fig. 12, we present a semi-log plot of the conductivity of AgPO₃ glass measured at 3.4 kHz as a function of temperature [31]. The figure includes a MIGRATION-type model curve, which reproduces the observed temperature dependence very well above ca. 180 K. Interestingly, the conductivity measured at lower temperatures shows a steadily increasing deviation from the second universality (i.e. from a horizontal line drawn at the value of σ at 0 K) which must be ascribed to NCL-type slightly activated processes.

Fig. 12

Temperature dependence of the ionic conductivity of AgPO₃ glass at 3.4 kHz [31]. For the two contributions to the total conductivity, see main text

Forming the difference between the measured total conductivity and the MIGRATION-type contribution, we obtain the bent line in Fig. 12. Empirically, this bent line is well described as the sum of the logarithm of the second-universality contribution and a second term, which is the logarithm of 1 + cT, where c is a constant. In a non-logarithmic plot of σ(T), this corresponds to a straight line, implying that the sum of all those contributions to the conductivity, which are due to slightly activated processes, increases linearly with temperature.

In short, we first decompose the total conductivity into its MIGRATION and NCL parts, written as σ _tot  = σ _MIG  + σ _NCL , and then regard σ _NCL as the sum of the second-universality component and an activated component, σ _NCL  = σ _2. univ  + σ _act . Moreover, on the basis of the data of Fig. 12, we may conclude that σ _act is approximately proportional to temperature, σ _act  ∝ T. A simple explanation for this will be given below.

Figure 13 shows that the same pattern is observed in AgPO₃ glass at other frequencies as well. The constant c is now found to be the same for each frequency. Again, we arrive at the important conclusion that σ _act and T are proportional to each other. As expected, the conductivity component due to strictly localized ionic movements increases linearly with frequency. Note that the MIGRATION-type component also increases with frequency, reflecting the first-universality-type dispersion, cf. Fig. 1.

Fig. 13

Temperature-dependent conductivities of AgPO₃ glass at the following four frequencies: 0.45 kHz (circles), 3.4 kHz (triangles), 17.3 kHz (diamonds), 87.8 kHz (squares) [31]. The components indicated in the figure correspond to those in Fig. 12

In the group of one of us (H.J.), ionic conductivities of a quaternary glass, 0.61 SiO₂ · 0.35 Li₂O · 0.03 Al₂O₃ · 0.01 P₂O₅, had been studied earlier in the impedance frequency regime, over a wide range of temperatures extending from 4 K to 298 K [32]. In Fig. 14, we present a data set taken at 10 kHz. Obviously, the resulting pattern is the same as in Fig. 12, while further data taken at other frequencies correspond to those of Fig. 13.

Fig. 14

Representation as in Fig. 12, but now for a glass of composition 0.61 SiO₂ ⋅ 0.35 Li₂O ⋅ 0.03 Al₂O₃ ⋅ 0.01 P₂O₅. The total conductivity marked by the dashed line is the calculated sum of σ _MIG and σ _NCL

In summary, the conductivity component due to slightly activated localized processes, σ _act , has been found to be proportional not only to angular frequency, but also to temperature. The latter proportionality can be attributed to a flat distribution of barrier heights, δ, encountered by the locally mobile ions. Then, the activated localized component is described by

$$ {\sigma}_{act}\left(\omega, T\right)\propto \omega \cdot {\displaystyle \underset{0}{\overset{\infty }{\int }} \exp \left(-\delta /{k}_BT\right) d\delta =\omega \cdot {k}_B}T. $$

(4)

Here, the linear dependence of conductivity on temperature results from the fact that there is no probability factor, f(δ), in the integral. In other words, a flat distribution of barriers corresponds to a situation where the probability for an ion to meet a barrier of height δ does not depend on the value of δ.

5 Implications of the localization of non-activated ionic motion

In this section, we address the second set of questions that were mentioned earlier.

In the first place, an experimental example will be given, documenting the very existence of a crossover of the low-temperature ionic conductivity from a linear to a quadratic frequency dependence, observed with decreasing frequency. More importantly, it will then be shown that such a crossover must always exist at low frequencies, being a consequence of the strictly localized motion of ions in voids of finite size.

Before presenting conductivity data displaying the sought-after change of slope from 2 to 1 in a log-log plot of its frequency dependence, we need to report on the detection of an unexpected low-temperature feature in x Na₂O ⋅ (1-x) B₂O₃ glasses, see Fig. 15 [12]. The figure contains three sets of temperature-dependent 87.8 kHz iso-frequency data, taken for glasses with different sodium contents. The maximum observed for x = 0 is the one already shown in Fig. 7 and discussed in the respective section. Clearly, it is not caused by the sodium ions. However, it is still seen to contribute to the conductivities measured on glasses with x = 0.05 and x = 0.1. In these glasses, the first-universality-type motion of the mobile sodium ions gives rise to a rapid increase of the conductivity above some 350 K. For x = 0.1, the figure includes a solid line obtained from the equations of the MIGRATION concept. For the same composition, a horizontal broken line represents the familiar effect of the second universality.

Fig. 15

Ionic conductivity versus temperature for three glasses x Na₂O ⋅ (1-x) B₂O₃ at 87.8 kHz. Experimental data are represented by open symbols. For x = 0.10, the MIGRATION concept has been used to specify the contribution due to hopping (solid line), while a second-universality component is indicated by the broken line

Once the above contributions are removed from the total conductivity of the x = 0.1 glass, a ‘low-temperature component’, σ _LTC (ν = 87.8 kHz, T), is seen to remain. This component displays a pronounced maximum at about 10 K and then decays with increasing temperature. Its decay strongly resembles the one observed for x = 0 above 210 K, which has been identified as indicative of the existence of a ‘two-to-one’ crossover at angular frequency ω ₁.

Exploiting the dependence of σ _LTC on both temperature and frequency, we have constructed the broadband conductivity isotherms presented in Fig. 16 [12] and, indeed, the ‘two-to-one’ crossover is now clearly visible. As in the case of nominally pure B₂O₃, this transition is much broader than expected from our modeling. The inset shows a set of three different isotherms. Evidently, the frequency-squared low-frequency part shifts in an activated fashion, the activation energy being (0.15 ± 0.02) eV.

Fig. 16

Broadband log-log representation of the frequency-dependent low-temperature conductivity component of 0.10 Na₂O ⋅ 0.90 B₂O₃ glass at 55 K. The inset also includes equivalent plots for 35 K and 75 K [12]

An important question has so far remained unanswered. It arises from the fact that no ‘two-to-one’ crossover is seen in Fig. 9 and that the familiar temperature-independent second-universality feature is also present in Fig. 15, see the horizontal broken line. Does one expect to see a behavior as displayed in Fig. 16 in these cases as well, although at lower frequencies?

There is a clear answer to this question. Indeed, the ‘two-to-one’ crossover is inevitably present. This implies in particular that, at sufficiently low frequencies, the horizontal broken line of Fig. 15 must take on a shape which is similar to the one displayed by the σ _LTC component below 100 K. In fact, the reason for this lies in the localization of any non-activated ionic motion and is best explained in terms of the mean square displacement of the locally mobile ions [12, 13].

To construct the time-dependent mean square displacement of the localized motion, 〈r ²(t)〉 _L , we need to integrate W _LOC (t), now called W _L (t), from t ′ = 0 to t ′ = t. In a first step, this will be done for true second-universality behavior, as specified by Fig. 2. This implies that ω ₁ is negligibly small and that ω ₂ is outside the experimental range at all temperatures considered, i.e., large and non-activated. In this limit, the expression of Eq. (3) becomes W _L (t) ≅ 1/(1 + ω ₂ t), and integration yields 〈r ²(t)〉 _L  ∝ ln(1 + ω ₂ t). Moreover, 〈r ²(t)〉 _L has to be proportional to k _B T, since the kinetic energy of the mobile ions and thus the square of their displacements are provided by the thermal energy. This leads us to

$$ {\left\langle {r}^2(t)\right\rangle}_L\propto {k}_BT\cdot \ln \left(1+{\omega}_2t\right). $$

(5)

When the corresponding conductivity is formed according to linear response theory [21], via

$$ {\sigma}_L\left(\omega, T\right)\propto \frac{1}{k_BT}\cdot FT\left\{\frac{d^2}{d{t}^2}{\left\langle {r}^2(t)\right\rangle}_L\right\}, $$

(6)

the term k _B T cancels out and σ _L becomes temperature-independent. At all angular frequencies that are well below ω ₂, the conductivity derived from Eq. (6) is, as expected, found to be of the second-universality type, σ _L (ω) ∝ ω.

Of course, 〈r ²(t)〉 _L tends to zero at very short times, cf. Eq. (5). At times well above 1/ω ₂, however, corresponding to the frequency range where the second universality is observed, 〈r ²(t)〉 _L becomes a linear function of ln(ω ₂ t), the slope being proportional to temperature, see Fig. 17. In view of Eq. 6, it is evident that the linear dependence shown in the plot of Fig. 17 and the second universality phenomenon are, indeed, equivalent [12, 13].

Fig. 17

Normalized mean square displacement as a function of time for an ion in its accessible volume. For details, see main text and Refs. [12, 13]

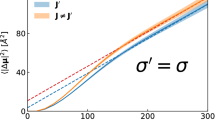
Figure 17 immediately guides us to an essential new insight. As only a finite local volume is accessible for each ion, there must be some limiting maximum value, 〈r ²(∞)〉 _L , which the mean square displacement approaches at long times, see Fig. 17. That crossover may be characterized by a crossover time, to be denoted by t = t ₁ = 1/ω ₁.

In a second step, W _L (t) is now written as in Eq. (3), with ω ₁ = 1/t ₁ inserted into it. By integration, a closed expression is then obtained for 〈r ²(t)〉 _L /〈r ²(∞)〉 _L , in the form of a continuous function of time [12, 13]. The three solid lines in Fig. 17 are plots of this function, pertaining to different temperatures.

Obviously, the crossover of the mean square displacement at t = t ₁ corresponds to a “two to one” crossover of σ _L (ω) at ω = ω ₁ = 1/t ₁, see Figs. 6c and 16. This convincingly answers the question we posed earlier, regarding the existence of such a crossover at sufficiently low frequencies.

The construction of Fig. 17 also provides the key for understanding the temperature dependence of the crossover angular frequency, ω ₁(T). According to the figure, ln(ω ₂ t ₁) = ln(ω ₂/ω ₁) is proportional to 1/T, and this implies

$$ {\omega}_1(T)={\omega}_2\cdot \exp \left(-\frac{E_1}{k_BT}\right), $$

(7)

with an apparent activation energy, E ₁, in agreement with the experimental findings of Fig. 16.

The main results obtained are the following. (i) The finite volume accessible for each ion necessitates the “two to one” crossover at angular frequency ω ₁, including its temperature dependence. (ii) The rate equation, Eq. (1), is reinterpreted without requiring a double minimum potential that is fixed in space. (iii) The lower panel of Fig. 10 still applies in the second-universality temperature regime, with the displacements involved varying with temperature as T ^1/2. (iv) The location at which each ion performs its non-activated forward-backward displacive movements is allowed to shift in space, yielding a logarithmic time dependence of the mean square displacement. (v) This shifting is restricted to the finite size of the accessible volume, provided for the ion by the network structure. (vi) The crossover times and angular frequencies, t ₁ and ω ₁, depend on the size of this volume. As a consequence, movements of ions contained in voids of different sizes may contribute second-universality components with “two to one” transitions located at quite different frequencies.

6 Conclusions

On our journey toward understanding the second universality we have had the pleasure of uncovering several fascinating features.

• (i) Non-vibrational conductivity spectra of disordered solid electrolytes are in general composed of two types of components, one being due to activated hopping processes of the mobile ions, the other being caused by strictly localized ionic movements, the latter displaying no or little temperature dependence.

• (ii) The contributions due to activated hopping can be removed from the spectra, opening up the possibility to study the remaining nearly-constant-loss component and the ionic movements causing it.

• (iii) An explanation of the NCL component does not require the assumption of a fixed distribution of asymmetric double-well potentials (ADWP). Rather, Coulomb interactions between locally mobile ions have been shown to create time-dependent single-particle potentials, thus causing the observed effects.

• (iv) A rate equation has been proposed, yielding the time-dependent mean square displacement of the locally mobile ions. Here, an important ingredient is the see-saw-type variation of the single-particle potentials, caused by the Coulomb interactions. The conductivity spectra thus obtained are in agreement with results from Monte Carlo simulations and also with experimental data. The latter include high-temperature high-frequency data from various crystalline and glassy ion conductors as well as conductivities measured on a system in which hydrogen ions perform slightly activated local movements.

• (v) The temperature dependence of NCL-type effects has been studied in various glasses. This includes the transition toward the second universality, which is the remaining feature at low temperatures and is indicative of the absence of any activation. During the transition, processes requiring thermal activation become less and less probable. The observed temperature dependence suggests a flat distribution of the heights of barriers that are encountered by locally mobile ions.

• (vi) An unexpected low-temperature component has been detected in iso-frequency conductivity data taken on sodium borate glasses such as 0.1 Na₂O ⋅ 0.9 B₂O₃. It corresponds to a crossover from the linear frequency dependence, which is characteristic of the second universality, to a quadratic one at low frequencies. In terms of our modeling, this crossover is equivalent to a crossover of the time-dependent mean square displacement of the locally mobile ions to a limiting maximum value at long times, which is given by the finite size of the accessible volume.