High-frequency stimulation induces axonal conduction block without generating initial action potentials

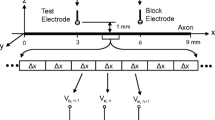
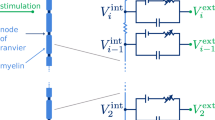
Abstract

The purpose of this modeling study is to develop a novel method to block nerve conduction by high frequency biphasic stimulation (HFBS) without generating initial action potentials. An axonal conduction model including both ion concentrations and membrane ion pumps is used to analyze the axonal response to 1 kHz HFBS. The intensity of HFBS is increased in multiple steps while maintaining the intensity at a sub-threshold level to avoid generating an action potential. Axonal conduction block by HFBS is defined as the failure of action potential propagation at the site of HFBS. The simulation analysis shows that step-increases in sub-threshold intensity during HFBS can successfully block axonal conduction without generating an initial response because the excitation threshold of the axon can be gradually increased by the sub-threshold HFBS. The mechanisms underlying the increase in excitation threshold involve changes in intracellular and extracellular sodium and potassium concentration, change in the resting potential, partial inactivation of the sodium channel and partial activation of the potassium channel by HFBS. When the excitation threshold reaches a sufficient level, an acute block occurs first and after additional sub-threshold HFBS it is followed by a post-stimulation block. This study indicates that step-increases in sub-threshold HFBS intensity induces a gradual increase in axonal excitation threshold that may allow HFBS to block nerve conduction without generating an initial response. If this finding is proven to be true in human, it will significantly impact clinical applications of HFBS to treat chronic pain.

Appendix

The total ionic current ${I}_{i,j}$ at the j^th segment is described as follows:

$${I}_{i,j}={I}_{Na}+{I}_{k}+{I}_{L}+{I}_{Na-p}+{I}_{K-p}$$

${I}_{Na}$ is the sodium (Na⁺) current; ${I}_{K}$ is the potassium (K⁺) current; ${I}_{L}$ is the leak current; ${I}_{Na-p}$ is the Na⁺ pump current. ${I}_{K-p}$ is the K⁺ pump current.

The Na⁺ current at j^th segment is described as:

$${I}_{Na}={G}_{Na}{m}^{3}h\left({V}_{j}-{V}_{Na}\right)$$

$${V}_{j}={E}_{j}-{E}_{rest}$$

$${V}_{Na}={E}_{Na}-{E}_{rest}$$

$${E}_{Na}=\frac{R*T}{F}ln\frac{{Na}_{ps}}{{Na}_{in}}$$

where ${G}_{Na}$ is the maximal Na⁺ conductance (120 ${{k\Omega }^{-1}cm}^{-2}$); m is the activation of Na⁺ channel; h is the inactivation of Na⁺ channel;${V}_{n}$ is the change of the membrane potential relative to the resting membrane potential ${E}_{rest}$; ${V}_{Na}$ is the reduced equilibrium membrane potential of Na⁺ ions after subtracting the resting membrane potential ${E}_{rest}$; ${E}_{Na}$ is the Na⁺ equilibrium potential; $R$ is the gas constant (8.3 $J/(mol*K)$); T is the temperature in Kelvin; F is the Faraday constant (96,485 $C/mol$). ${Na}_{in}$ is the Na⁺ concentration inside the axon with an initial value of 50 $mmol/L$; ${Na}_{ps}$ is the Na⁺ concentration outside the axon in the periaxonal space with an initial value of $440 mmol/L$ that equals to the constant Na⁺ concentration in the large extracellular space (${Na}_{o}$). The periaxonal space consists of a very thin layer of fluid (thickness of $\mathrm{} 1.45\times {10}^{-2} \mu m$) that separates the axonal membrane from the large extracellular space (Frankenhaeuser & Hodgkin, 1952; Scriven, 1981; Whitwam & Kidd, 1975). Ions can diffuse between the periaxonal space and the large extracellular space where the ion concentrations are maintained constant.

The K⁺ current at j^th segment is described as:

$${I}_{K}={G}_{K}{n}^{4}\left({V}_{j}-{V}_{K}\right)$$

$${V}_{K}={E}_{K}-{E}_{rest}$$

$${E}_{K}=\frac{R*T}{F}ln\frac{{K}_{ps}}{{K}_{in}}$$

where ${G}_{K}$ is the maximal K⁺ conductance (36 ${{k\Omega }^{-1}cm}^{-2}$); n is the activation of K⁺ channel; ${V}_{K}$ is reduced equilibrium membrane potential of K⁺ ions after subtracting the resting membrane potential ${E}_{rest}$; ${E}_{K}$ is the K⁺ equilibrium potential; ${K}_{in}$ is the K⁺ concentration inside the axon with an initial value of 400 $mmol/L$; ${K}_{ps}$ is the K⁺ concentration outside the axon in the periaxonal space with an initial value of $20 mmol/L$ that equals the constant K⁺ concentration in the large extracellular space (${K}_{o}$).

At resting membrane potential $({V}_{j}=0 mV)$, the total ionic current across the membrane $({I}_{i,j})$ should be zero. Since at resting membrane potential ${I}_{Kp}={-I}_{K}, {I}_{Nap}={-I}_{Na}$, the leakage current at j^th segment is described as follows:

$${I}_{L}={G}_{L}*{V}_{j}$$

where ${G}_{L}$ is the maximal conductance (0.3 ${{k\Omega }^{-1}cm}^{-2}$) of the leakage current.

The resting membrane potential ${E}_{rest}$ is described by modified Goldman equation as follows (Mullins & Noda, 1963; Scriven, 1981):

$${E}_{rest}=\frac{R*T}{F}ln\frac{ r{K}_{ps}+e{Na}_{ps }}{ r{K}_{in}+e{Na}_{in}}$$

where r is the Na–K pump ratio (Mullins & Brinley, 1969) and e is a constant (0.0566) representing the ratio of Na⁺ and K⁺ permeability.

$$r={c}_{r}N{a}_{in}+{d}_{r}$$

where ${c}_{r}$ and ${d}_{r}$ are constants; In the squid axon ${c}_{r}$ has a value of 0.05 (Mullins & Brinley, 1969) and ${d}_{r}$ has a value of -1 since at initial resting state $r=1.5$ (Thomas, 1972) and $N{a}_{in}=50$.

The currents of Na⁺ and K⁺ pumps are described as (Mullins & Brinley, 1969; Scriven, 1981):

$${I}_{K-p}=-\frac{a}{{\left(1+{b}_{1}/{K}_{ps}\right)}^{2}\left(1+{b}_{2}/{Na}_{in}\right)}$$

$${I}_{Na-p}=-r{I}_{K-p}$$

where $a$ is a constant (0.0954). ${b}_{1}$ is the dissociation constant for ${K}_{ps}$, and ${b}_{2}$ is the dissociation constant for ${Na}_{in}$. The constants ${b}_{1}$ and ${b}_{2}$ are estimated to be 1 $mmol/L$ and 30 $mmol/L$, respectively (Mullins & Brinley, 1969; Rang & Ritchie, 1968).

The evolution equations for $m, h, n$ are described as following (Hodgkin & Huxley, 1952; Scriven, 1981):

$$\frac{dm}{dt}={\alpha }_{m}\left(1-m\right)-{\beta }_{m}m$$

$$\frac{dh}{dt}={\alpha }_{h}\left(1-h\right)-{\beta }_{h}h$$

$$\frac{dn}{dt}={\alpha }_{n}\left(1-n\right)-{\beta }_{n}n$$

$${\alpha }_{m}=\Phi \bullet \frac{2.5-0.1({\mathrm{V}}_{\mathrm{j}}-ms)}{\mathrm{exp}(2.5-0.1{\mathrm{V}}_{\mathrm{j}})-1}$$

$${\beta }_{m}=\Phi \bullet 4\mathrm{exp}\left(-\frac{{\mathrm{V}}_{\mathrm{j}}-ms}{18}\right)$$

$${\alpha }_{h}=\Phi \bullet 0.07\mathrm{exp}\left(-\frac{{\mathrm{V}}_{\mathrm{j}}-hs}{20}\right)$$

$${\beta }_{h}=\Phi \bullet \frac{1}{\mathrm{exp}(3.0-0.1({\mathrm{V}}_{\mathrm{j}}-hs))+1}$$

$${\alpha }_{n}=\Phi \bullet \frac{0.1(1-0.1({\mathrm{V}}_{\mathrm{j}}-ns))}{\mathrm{exp}(1-0.1({\mathrm{V}}_{\mathrm{j}}-ns))-1}$$

$${\beta }_{n}=\Phi \bullet 0.125\mathrm{exp}(-\frac{{\mathrm{V}}_{\mathrm{j}}-ns}{80})$$

$$\Phi ={3}^{\left(T-279.3\right)/10}$$

where $ms, hs, ns$ are constants that equal 7.8, 3.1, 18.5, respectively. The initial values for m, h, n are 0.0204, 0.6988, and 0.1, respectively. $\Phi$ is the coefficient of temperature.

The evolution equations for ${Na}_{in}, {K}_{in}, {Na}_{ps}, {K}_{ps}$ are described as follows (Frankenhaeuser & Hodgkin, 1956; Scriven, 1981):

$$\frac{{dNa}_{in}}{dt}=\frac{-4\times \left({I}_{Na}+{I}_{Na-p}\right)}{F\times d}$$

$$\frac{{dK}_{in}}{dt}=\frac{-4\times ({I}_{K}+{I}_{K-p})}{F\times d}$$

$$\frac{{dNa}_{ps}}{dt}=\frac{{(\mathrm{I}}_{\mathrm{Na}-\mathrm{p}}{+\mathrm{I}}_{\mathrm{Na}})/\mathrm{F}-{\mathrm{D}}_{\mathrm{Na}}({\mathrm{Na}}_{\mathrm{ps}}{-\mathrm{Na}}_{\mathrm{o}})}{\uptheta }$$

$$\frac{{dK}_{ps}}{dt}=\frac{{(\mathrm{I}}_{\mathrm{K}-\mathrm{p}}{+\mathrm{I}}_{\mathrm{K}})/\mathrm{F}-{\mathrm{D}}_{\mathrm{K}}({\mathrm{K}}_{\mathrm{ps}}{-\mathrm{K}}_{\mathrm{o}})}{\uptheta }$$

where D_Na $and$ D_K are diffusion constants for Na⁺ (0.1 $\mu m/s$) and K⁺ (0.1 $\mu m/s$) to diffuse between the periaxonal space and the large extracellular space, respectively. $\uptheta$ ($1.45\times {10}^{-2} \mu m$) is the thickness of the periaxonal space (Frankenhaeuser & Hodgkin, 1956; Scriven, 1981).