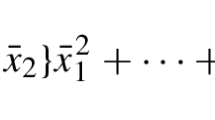The combinatorics of weight systems and characteristic polynomials of isolated quasihomogeneous singularities

Abstract

A paper of the first author and Zilke proposed seven combinatorial problems around formulas for the characteristic polynomial and the exponents of an isolated quasihomogeneous singularity. The most important of them was a conjecture on the characteristic polynomial. Here, the conjecture is proved, and some of the other problems are solved, too. In the cases where also an old conjecture of Orlik on the integral monodromy holds, this has implications on the automorphism group of the Milnor lattice. The combinatorics used in the proof of the conjecture consists of tuples of orders on sets $\{0,1,\ldots ,n\}$ with special properties and may be of independent interest.

1 Introduction

The paper [10] proposed seven combinatorial problems around formulas for the characteristic polynomial and the exponents of an isolated quasihomogeneous singularity. Problem 6 was a conjecture on the characteristic polynomial. It was an amendment to an old conjecture of Orlik on the integral monodromy (which is recalled below). Here the conjecture on the characteristic polynomial is proved, and also some of the other combinatorial problems are solved.

The combinatorics which is used in the proof of the conjecture was found in [9] and was used there for a partial proof of Orlik’s conjecture. It is described in detail in Sect. 2. It may be of independent interest.

In this introduction the conjecture and some background are explained. This contains problem 6 in [10]. Problem 7 in [10] is treated in Sect. 3. Section 4 sets some notations and notions. Section 5 solves problem 1. Section 6 discuss the combinatorics of the weight systems and of the characteristic polynomial of an isolated quasihomogeneous singularity. It solves problem 4 and discusses the problems 2, 3 and 5.

We start with the notion of an Orlik block and a result on its automorphisms. Then, we introduce isolated quasihomogenous singularities. Finally, we give Theorem 1.5, which solves problem 6 in [10], and Orlik’s conjecture.

Definition 1.1

Let $M\subset {\mathbb {N}}=\{1,2,3,\ldots \}$ be a finite nonempty subset. Its Orlik block is a pair $(H_M,h_M)$ with $H_M$ a ${\mathbb {Z}}$-lattice of rank $\sum _{m\in M}\varphi (m)$ and $h_M:H_M\rightarrow H_M$ an automorphism with characteristic polynomial $\prod _{m\in M}\varPhi _m$ ($\varPhi _m$ is the m-th cyclotomic polynomial) and with a cyclic generator $e_1\in M$, i.e.,

$$\begin{aligned} H_M =\bigoplus _{j=1}^{rk M}{\mathbb {Z}}\cdot h_M^{j-1}(e_1). \end{aligned}$$

(1.1)

The pair $(H_M,h_M)$ is unique up to isomorphism. $\mathrm{Aut}_{S^1}(H_M,h_M)$ denotes the group of all automorphisms of $H_M$ which commute with $h_M$ and which have all eigenvalues in $S^1$.

Remark 1.2

Consider an Orlik block $(H_M,h_M)$.

(i) Each endomorphism of $(H_M,h_M)$ (so each endomorphism of $H_M$ which commutes with $h_M)$ is of the form $c(h_M)$ with $c(t)\in {\mathbb {Z}}[t]$ because of the cyclic structure. Consider such an endomorphism $c(h_M)$, and consider an eigenspace in $H_{M,{\mathbb {C}}}:=H_M\otimes _{\mathbb {Z}}{\mathbb {C}}$ of $h_M$ with eigenvalue $\lambda$ with $\mathrm{ord\, }(\lambda )\in M$ (this eigenspace is one-dimensional). $c(h_M)$ acts on it as $c(\lambda )\cdot \mathrm{id}$. If $c(h_M)\in \mathrm{Aut}_{S^1}(H_M,h_M)$, then $c(\lambda )\in {\mathbb {Z}}[\lambda ]\cap S^1=\{\pm \lambda ^k\,|\, k\in {\mathbb {Z}}\}$. Therefore, each element of $\mathrm{Aut}_{S^1}(H_M,h_M)$ is of finite order, and the group $\mathrm{Aut}_{S^1}(H_M,h_M)$ is finite.

(ii) Theorem 1.4 states when $\mathrm{Aut}_{S^1}(H_M,h_M)=\{\pm h_M^k\,|\, k\in {\mathbb {Z}}\}$. In general, this does not hold. Here is one example. Other examples are in [5, Examples 1.4 (iv) and (v)]. Consider $M:=\{3,5\}$. Then, in fact (see e.g., Lemma 6.1 in [5])

$$\begin{aligned} (H_M,h_M)\cong & {} (H_{\{3\}},h_{\{3\}})\oplus (H_{\{5\}},h_{\{5\}})\\ \mathrm{Aut}_{S^1}(H_M,h_M)\cong & {} \mathrm{Aut}_{S^1}(H_{\{3\}},h_{\{3\}}) \times \mathrm{Aut}_{S^1}(H_{\{5\}},h_{\{5\}})\\\cong & {} \{\pm h_{\{3\}}^k\,|\, k\in \{0,1,2\}\}\times \{\pm h_{\{5\}}^k\,|\, k\in \{0,1,2,3,4\}\}\quad (60\text { elements})\\&\supsetneqq&\{\pm h_M^k\,|\, k\in \{0,1,\ldots ,14\}\}\quad (30\text { elements}). \end{aligned}$$

Definition 1.3

A finite set $M\subset {\mathbb {N}}$ is enriched as follows to a directed graph (M, E(M)) with set of vertices M and set of oriented edges $E(M)\subset M\times M$. An edge goes from $m_1\in M$ to $m_2\in M$ if $\frac{m_1}{m_2}$ is a power of a prime number p. Then, it is called a p-edge.

The main result in [5] is as follows.

Theorem 1.4

[5, Theorem 1.2] Let $(H_M,h_M)$ be the Orlik block of a finite nonempty subset $M\subset {\mathbb {N}}$. Then, $\mathrm{Aut}_{S^1}(H_M,h_M)=\{\pm h_M^k\, |\, k\in {\mathbb {Z}}\}$ if and only if condition (I) or condition (II) in Definition 2.8 (c) and (d) are satisfied. They are conditions on the graph (M, E(M)).

The conditions (I) and (II) in Definition 2.8 (c) and (d) are quite technical. After Definition 2.8, it is discussed why they are both not satisfied in the example in Remark 1.2 (ii), and examples where condition (I) is satisfied are given.

A weight system $\mathbf{w}=(w_1,\ldots ,w_n;1)$ with $w_i\in {\mathbb {Q}}_{>0}\cap (0,1)$ equips any monomial $\mathbf{x}^\mathbf{j}=x_1^{j_1}\ldots x_n^{j_n}$ with a weighted degree $\deg _\mathbf{w}{} \mathbf{x}^\mathbf{j}:=\sum _{i=1}^n w_ij_i$. A polynomial $f\in {\mathbb {C}}[x_1,\ldots ,x_n]$ is an isolated quasihomogeneous singularity if for some weight system $\mathbf{w}$ each monomial in f has weighted degree 1 and if the functions $\frac{\partial f}{\partial x_1},\ldots ,\frac{\partial f}{\partial x_n}$ vanish simultaneously only at $0\in {\mathbb {C}}^n$. Then, the Milnor lattice $H_{Mil}:=H_{n-1}(f^{-1}(1),{\mathbb {Z}})$ (resp. the reduced homology in the case $n=1$) is a ${\mathbb {Z}}$-lattice of some rank $\mu \in {\mathbb {N}}$ [14], which is called Milnor number. It comes equipped with a natural automorphism $h_{Mil}:H_{Mil}\rightarrow H_{Mil}$ of finite order, the monodromy. Its characteristic polynomial has the shape

$$\begin{aligned} p_{ch,h_{Mil}}&= \prod \limits _{m\in {\mathbb {N}}}\varPhi _m^{\psi (m)} \end{aligned}$$

for a function $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ with finite support $M_1:=\{n\in {\mathbb {N}}\,|\, \psi (n)\ne 0\}$. Denote $l_\psi :=\max (\psi (m)\, |\, m\in {\mathbb {N}})$ and for $j=1,\ldots ,l_\psi$

$$\begin{aligned} M_j:=\{m\in {\mathbb {N}}\, |\, \psi (m)\ge j\}. \end{aligned}$$

The tuple $(M_1,\ldots ,M_{l_\psi })$ is called standard covering of $\psi$. It satisfies (and is determined by this)

$$\begin{aligned} M_1\supset M_2\supset \cdots \supset M_{l_\psi }\ne \emptyset , \quad \psi (m)=|\{j\in \{1,\ldots ,l_\psi \}\,|\, m\in M_j\}|. \end{aligned}$$

The most important result in this paper is Theorem 1.5.

Theorem 1.5

Consider an isolated quasihomogeneous singularity f as above and the sets $M_1,\ldots ,M_{l_\psi }$ as above.

• (a) Each set $M_j$ satisfies condition (I) in Definition 2.8 (c).

• (b) $\mathrm{Aut}_{S^1}(H_{M_j},h_{M_j})=\{\pm h_{M_j}^k\,|\,k\in {\mathbb {Z}}\}.$

Proof

Part (b) follows from part (a) and Theorem 1.4. Part (a) follows from Lemma 2.10 and Theorem 6.7. Lemma 2.10 says that a finite set $M\subset {\mathbb {N}}$ which is compatible with a tuple of excellent orders (Definition 2.5 (d)) satisfies condition (I). Theorem 6.7 says that in the case of an isolated quasihomogeneous hypersurface singularity each set $M_j$ is compatible with a certain tuple of excellent orders. It was proved in [9]. There it is Theorem 12.1. Its proof uses two classical results on isolated quasihomogeneous singularities, Theorems 6.1 and 6.4 (a). Kouchnirenko’s Theorem 6.1 characterizes combinatorially those weight systems $\mathbf{w}$ for which generic polynomials of weighted degree 1 have an isolated singularity. Theorem 6.4 (a) of Milnor and Orlik gives in this case a formula for the characteristic polynomial $p_{ch,h_{Mil}}$ of the monodromy in terms of the weight system $\mathbf{w}$. More on the proof of Theorem 6.7 is said directly before Theorem 6.7. $\square$

Problem 6 in [10] asked precisely about part (a) of Theorem 1.5. The notion of an excellent order and the notion of compatibility of a finite set $M\subset {\mathbb {N}}$ with a tuple of excellent orders were first used in [9, Sect. 9]. We found them when we searched for a partial proof of Orlik’s conjecture. They are recalled in Sect. 2.

Theorem 1.5 is independent of Orlik’s conjecture. But it is useful only in the cases where Orlik’s conjecture holds. $\square$

Conjecture 1.6

(Orlik’s conjecture, [16, conjecture 3.1]) For any isolated quasihomogeneous singularity, there is an isomorphism

$$\begin{aligned} (H_{Mil},h_{Mil})\cong \bigoplus _{j=1}^{l_\psi } (H_{M_j},h_{M_j}). \end{aligned}$$

A direct sum of Orlik blocks $(H_{M_j},h_{M_j})$ with sets $M_j$ which satisfy $M_1\supset \cdots \supset M_{l_\psi }$ is called a standard decomposition into Orlik blocks [9, Definition 1.1(e)]. Orlik’s conjecture says that the pair $(H_{Mil},h_{Mil})$ of an isolated quasihomogeneous singularity allows a standard decomposition into Orlik blocks.

The papers [8] and [9] give partial positive results. They are cited in Theorem 1.7. They surpass all known cases.

Theorem 1.7

[9, Theorem 1.3] (a) Orlik’s conjecture holds for the chain-type singularities.

(b) (Also [8, Theorem 1.3]) Orlik’s conjecture holds for the cycle-type singularities.

(c) Let $f=f(x_1,\ldots ,x_{n_f})$ and $g=g(x_{n_f+1},\ldots ,x_{n_f+n_g})$ be two isolated quasihomogeneous singularities in different variables, which both satisfy Orlik’s conjecture. Then, also $f+g$ satisfies Orlik’s conjecture.

(d) Orlik’s conjecture holds for all iterated Thom–Sebastiani sums of chain-type singularities and cycle-type singularities.

The notions chain-type singularity and cycle-type singularity are explained for example in [7, ch. 3] [10, ch. 4] [9, ch. 10+11]. The notion Thom–Sebastiani sum is discussed in Sect. 3. The iterated Thom–Sebastiani sums of chain-type singularities and cycle-type singularities form a large and important family of isolated quasihomogeneous singularities, but by far not all.

In those isolated quasihomogeneous singularities, where Orlik’s conjecture holds, $(H_{Mil},h_{Mil})$ decomposes (not uniquely in general) into Orlik blocks $(H_{M_j},h_{M_j})$, and Theorem 1.5 says that the group of automorphisms with eigenvalues in $S^1$ of each of these blocks is the smallest possible, it is $\{\pm h_{M_j}^k\,|\, k\in {\mathbb {Z}}\}$. This is very helpful also in determining the group of all automorphisms of the triple $(H_{Mil},h_{Mil},L_{Mil})$ where $L_{Mil}:H_{Mil}\times H_{Mil}\rightarrow {\mathbb {Z}}$ is the Seifert form. This group is important for period maps and Torelli conjectures for singularities (e.g., [4]).

Problem 7 in [10] is a strengthening of problem 6 and is also solved by Lemma 2.10 and the results in [9, Sect.  9]. This is explained in Sect. 3. The other problems 1–5 in [10] are discussed in Sects. 5 and 6.

Notations 1.8

${\mathbb {N}}=\{1,2,3,..\}$, ${\mathbb {N}}_0=\{0,1,2,..\}$. Always $m\in {\mathbb {N}}$ and $n\in {\mathbb {N}}$. For $I\subset {\mathbb {R}}$, ${\mathbb {Z}}_I:={\mathbb {Z}}\cap I$. The support of a map $\psi :{\mathbb {N}}\rightarrow {\mathbb {Q}}$ is the set $\mathrm{supp\, }(\psi ):=\{m\in {\mathbb {N}}\,|\, \psi (m)\ne 0\}$. We will consider only maps $\psi :{\mathbb {N}}\rightarrow {\mathbb {Q}}$ with finite support. Most often, $\psi$ will be a map $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ with finite support.

The set of all prime numbers is ${{\mathscr {P}}}\subset {\mathbb {N}}$. For $p\in {{\mathscr {P}}}$ and $m\in {\mathbb {N}}$, $v_p(m)\in {\mathbb {N}}_0$ is the unique number with $m=\prod _{q\in {{\mathscr {P}}}}q^{v_q(m)}$. Also the projection

$$\begin{aligned} \pi _p:{\mathbb {N}}\rightarrow \{n\in {\mathbb {N}}\,|\, p\not | n\},\quad m\mapsto m\cdot p^{-v_p(m)}, \end{aligned}$$

will be used.

2 Compatibility of a finite set of natural numbers with a tuple of excellent orders

This section proposes and discusses a condition for a finite set $M\subset {\mathbb {N}}$ of natural numbers and a condition for a map $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ with finite support. They are given in Definition 2.5 (d) and (e). They have a number of good properties, which are given in Lemma 2.6, Lemma 2.10, and Theorems 3.2 and 3.6. This is prepared by several definitions. Definitions 2.1, 2.3 and 2.5, Lemma 2.6, and Theorems 3.2 and 3.6 are recalled from [9, Sect.  9]. Definition 2.8 is recalled from [5]. Lemma 2.10 is new. It connects the condition in Definition 2.5 (d) for a finite set $M\subset {\mathbb {N}}$ with condition (I) (in Theorem 1.4 and Definition 2.8 (c)).

Definition 2.1

[9, 9.1] (a) An excellent order $\succ$ on a set ${\mathbb {Z}}_{[0,s(\succ )]}$ for some bound $s(\succ )\in {\mathbb {N}}_0$ is a strict order (so transitive and for all $a,b\in {\mathbb {Z}}_{[0,s(\succ )]}$ either $a=b$ or $a\succ b$ or $b\succ a$) which is determined by the set

$$\begin{aligned} S(\succ ):= & {} \{k\in {\mathbb {Z}}_{[0,s(\succ )]}\, |\, k\succ 0\} \end{aligned}$$

(2.1)

in the following way:

$$\begin{aligned} \left. \begin{array}{l} \succ \text { equals }>\text { on }S(\succ )\cup \{0\},\\ \succ \text { equals }<\text { on } {\mathbb {Z}}_{[0,s(\succ )]}-S(\succ ).\end{array}\right\} \end{aligned}$$

(2.2)

($S(\succ )=\emptyset$ is allowed.) The maximal element of ${\mathbb {Z}}_{[0,s(\succ )]}$ with respect to $\succ$ is called $s^+(\succ )$, so $s^+(\succ )\succ k$ for any other element $k\in {\mathbb {Z}}_{[0,s(\succ )]}$.

(b) The trivial excellent order is $\succ _0$ with $s(\succ _0):=0$, so it is the empty order on ${\mathbb {Z}}_{[0,s(\succ _0)]}=\{0\}$ (and, of course $S(\succ _0)=\emptyset$).

(c) The tensor product of two excellent orders $\succ _1$ and $\succ _2$ is the excellent order $\succ _1\otimes \succ _2$ with

$$\begin{aligned} s(\succ _1\otimes \succ _2):= & {} \max (s(\succ _1),s(\succ _2)) \quad \text {and} \end{aligned}$$

(2.3)

$$\begin{aligned} S(\succ _1\otimes \succ _2):= & {} (S(\succ _1)\cup S(\succ _2))-(S(\succ _1)\cap S(\succ _2)). \end{aligned}$$

(2.4)

Example 2.2

[9, 9.2] (i) The excellent order $\succ _1$ with $s(\succ _1)=7$ and $S(\succ _1)=\{6,4,1\}$ is given by

$$\begin{aligned} s^+(\succ _1)=6\succ _1 4\succ _1 1\succ _1 0 \succ _1 2 \succ _1 3\succ _1 5\succ _1 7. \end{aligned}$$

(ii) The excellent order $\succ _2$ with $s(\succ _2)=6$ and $S(\succ _2)=\{6,5,2,1\}$ is given by

$$\begin{aligned} s^+(\succ _2)=6\succ _2 5\succ _2 2\succ _2 1 \succ _2 0\succ _2 3\succ _2 4. \end{aligned}$$

(iii) The excellent order $\succ _3:=(\succ _1\otimes \succ _2)$ for $\succ _1$ and $\succ _2$ in (i) and (ii) satisfies $s(\succ _3)=7$, $S(\succ _3)=\{5,4,2\}$ and is given by

$$\begin{aligned} 5\succ _3 4\succ _3 2\succ _3 0 \succ _3 1\succ _3 3\succ _3 6 \succ 7. \end{aligned}$$

(iv) For any excellent order $\succ$, the tensor product with the trivial excellent order is $\succ$ itself, $\succ \otimes \succ _0=\succ$.

Definition 2.3

[9,  9.3] (a) A path in a finite directed graph (V, E) (so V is a finite non-empty set and $E\subset V\times V$) is a tuple $(v_1,\ldots ,v_l)$ for some $l\in {\mathbb {Z}}_{[2,\infty )}$ with $v_j\in V$ and $(v_j,v_{j+1})\in E$ for $j\in {\mathbb {Z}}_{[1,l-1]}$. It is a path from $v_1$ to $v_l$, so with source $v_1$ and target $v_l$.

(b) A finite directed graph (V, E) has a center $v_V\in V$ if it has no path from any vertex to itself and if it has at least one path from $v_V$ to any other vertex $v\in V$. (The center is unique, which justifies the notation $v_V$.)

(c) Consider a tuple $(\succ _p)_{p\in P}$ of excellent orders for a finite set $P\subset {{\mathscr {P}}}$ of prime numbers. It defines a finite directed graph $(V,E_V)$ with center $v_V$ as follows. Its set $V=V((\succ _p)_{p\in P})$ of vertices is the quadrant in ${\mathbb {N}}$

$$\begin{aligned}&V:= \left\{ \prod _{p\in P}p^{k_p}\,|\, k_p\in {\mathbb {Z}}_{[0,s(\succ _p)]}\right\} . \end{aligned}$$

(2.5)

Its set of edges $E_V=E((\succ _p)_{p\in P})$ is the set

$$\begin{aligned} E_V:= & {} \bigcup _{p\in P}E_{V,p}\text { with } \nonumber \\ E_{V,p}:= & {} \{(m_a,m_b)\in V\times V\,|\, \pi _p(m_a)=\pi _p(m_b), v_p(m_a)\succ _p v_p(m_b)\}. \end{aligned}$$

(2.6)

The edges in $E_{V,p}$ are called p-edges. So, the underlying undirected graph coincides with the undirected graph which underlies the directed graph (V, E(V)) in Definition 1.3. But the directions of edges may have changed. The graph $(V,E_V)$ is obviously centered with center

$$\begin{aligned} v_V=\prod _{p\in P}p^{s^+(\succ _p)}. \end{aligned}$$

(2.7)

Example 2.4

Consider the tuple $(\succ _3,\succ _5)$ of excellent orders with $s(\succ _3)=s(\succ _5)=2$ and $S(\succ _3)=\{2\}$, $S(\succ _5)=\{1\}$, so $2\succ _3 0\succ _3 1$ and $1\succ _5 0 \succ _5 2$. Here $P=\{3,5\}$ and $V=\{3^i5^j\,|\, i,j\in \{0,1,2\}\}=\{1,3,9,5,15,45,25,75,225\}$. The graphs (V, E(V)) from Definition 1.3 and $(V,E_V)$ from Definition 2.3 (c) are as follows:

The underlying undirected graphs coincide. The center of $(V,E_V)$ is $v_V=45$.

Definition 2.5

[9, 9.4] (a) Let $\succ$ be an excellent order on the set ${\mathbb {Z}}_{[0,s(\succ )]}$. A set $K\subset {\mathbb {N}}_0$ is subset compatible with $\succ$ if a bound $k_K\in {\mathbb {Z}}_{[0,s(\succ )]}$ with

$$\begin{aligned} K= & {} \{k\in {\mathbb {Z}}_{[0,s(\succ )]}\, |\, k\succ k_K\} \end{aligned}$$

(2.8)

exists or if $K={\mathbb {Z}}_{[0,s(\succ )]}$. (The bound $k_K=s^+(\succ )$ gives $K=\emptyset$, which is allowed.)

(b) For a finite non-empty set $M\subset {\mathbb {N}}$, let

$$\begin{aligned} {{\mathscr {P}}}(M):= & {} \{p\in {{\mathscr {P}}}\,|\, M\ne \pi _p(M)\}\nonumber \\= & {} \{p\in {{\mathscr {P}}}\,|\, \exists \ m\in M with v_p(m)>0\} \end{aligned}$$

(2.9)

be the set of prime numbers which turn up as factors of some numbers in M.

(c) For a finite non-empty set $M\subset {\mathbb {N}}$, a prime number $p\in {{\mathscr {P}}}$, and a number $m_0\in \pi _p(M)$, define the finite set $K_{M,p,m_0}\subset {\mathbb {N}}_0$ by

$$\begin{aligned} (\pi _p|_M)^{-1}(m_0)=\{m_0\cdot p^k\,|\, k\in K_{M,p,m_0}\}. \end{aligned}$$

(2.10)

(d) A finite non-empty set $M\subset {\mathbb {N}}$ is compatible with a tuple $(\succ _p)_{p\in P}$ of excellent orders for a finite set $P\supset {{\mathscr {P}}}(M)$ of prime numbers if

$$\begin{aligned} M\subset & {} V((\succ _p)_{p\in P}) \end{aligned}$$

(2.11)

and if for any prime number $p\in {{\mathscr {P}}}(M)$ and any $m_0\in \pi _p(M)$ the set $K_{M,p,m_0}$ is subset compatible with $\succ _p$. (So, here the excellent orders $\succ _p$ for $p\in {{\mathscr {P}}}-{{\mathscr {P}}}(M)$ are irrelevant. But considering $P\supset {{\mathscr {P}}}(M)$ instead of $P={{\mathscr {P}}}(M)$ will be useful.)

(e) A map $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ with finite support $\mathrm{supp\, }(\psi )\subset {\mathbb {N}}$ is compatible with a tuple $(\succ _p)_{p\in P}$ of excellent orders for a finite set $P\supset {{\mathscr {P}}}(\mathrm{supp\, }(\psi ))$ of prime numbers if

$$\begin{aligned} \mathrm{supp\, }(\psi )\subset & {} V((\succ _p)_{p\in P}) \end{aligned}$$

(2.12)

and if for any edge $(m_a,m_b)\in E_V$

$$\begin{aligned} \psi (m_a)\ge & {} \psi (m_b). \end{aligned}$$

(2.13)

(f) A covering of a map $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ with finite support is a tuple $(M_1,\ldots ,M_l)$ ($l\in {\mathbb {N}}_0$) of finite non-empty sets $M_j\subset {\mathbb {N}}$ with

$$\begin{aligned} \psi (m)= & {} |\{j\in \{1,\ldots ,l\}\,|\, m\in M_j\}| for any m\in {\mathbb {N}}. \end{aligned}$$

(2.14)

Here, obviously $l\ge \max (\psi (m)\,|\, m\in {\mathbb {N}}_0)=:l_\psi$. In the case $\mathrm{supp\, }(\psi )=\emptyset$, we have $l=0$ and an empty tuple. The standard covering of $\psi$ is the tuple $(M_1^{(st)},\ldots ,M_{l_\psi }^{(st)})$ with

$$\begin{aligned} M_j^{(st)}=\{m\in \mathrm{supp\, }(\psi )\,|\, \psi (m)\ge j\} for j\in \{1,\ldots ,l_\psi \}. \end{aligned}$$

(2.15)

It is the unique covering with $M_1\supset \cdots \supset M_l$, and it satisfies $M_1^{(st)}=\mathrm{supp\, }(\psi )$.

(g) Let $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ have finite support, let $P\supset {{\mathscr {P}}}(\mathrm{supp\, }(\psi ))$ be a finite set of prime numbers, and let $(\succ _p)_{p\in P}$ be a tuple of excellent orders with (2.12). A covering $(M_1,\ldots ,M_l)$ of $\psi$ is called compatible with $(\succ _p)_{p\in P}$ if each set $M_j$ is compatible with $(\succ _p)_{p\in P}$.

The following lemma expresses the compatibility conditions in Definition 2.5 (d) and (e) in a different way, and it shows their relationship. The proof is not difficult. It is given in [9].

Lemma 2.6

[9, 9.5] (a) Let $M\subset {\mathbb {N}}$ be a finite non-empty set, let $P\supset {{\mathscr {P}}}(M)$ be a finite set of prime numbers, and let $(\succ )_{p\in P}$ be a tuple of excellent orders with (2.11). (Recall the definition of $(V,E_V,v_V)$ in Definition 2.3 (c).) The following three conditions are equivalent:

• (i) M is compatible with $(\succ )_{p\in P}$.

• (ii) $(M,E_V\cap M\times M)$ is a directed graph with center $v_V$ (so $v_V\in M$), and if M contains the target of a path in $(V,E_V)$, it contains all vertices in this path.

• (iii) If $m_b\in M$ and $(m_a,m_b)\in E_V$, then $m_a\in M$.

(b) Let $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ be a map with finite support, let $P\supset {{\mathscr {P}}}(\mathrm{supp\, }(\psi ))$ be a finite set of prime numbers, and let $(\succ _p)_{p\in P}$ be a tuple of excellent orders with (2.12). The following three conditions are equivalent.

• (i) $\psi$ is compatible with $(\succ _{p})_{p\in P}$.

• (ii) $\psi$ has a covering $(M_1,\ldots ,M_l)$ which is compatible with $(\succ _{p})_{p\in P}$.

• (iii) The standard covering of $\psi$ is compatible with $(\succ _p)_{p\in P}$.

Example 2.7

The graph $(V,E_V)$ in Example 2.4 can also be shown as in the following left picture. The middle picture shows the set V, and the right picture is a graphical description of V. A subset $M\subset V$ is described in a similar way, with bullet points for its elements and small circles for the elements of $V-M$.

The following 19 pictures describe the subsets $M\subset V$ which are compatible with the tuple $(\succ _3,\succ _5)$ of excellent orders. One sees Definition 2.5 (d) and the characterizations in Lemma 2.6 (a).

Lemma 2.6 (a) allows to prove in Lemma 2.10 that any finite non-empty set $M\subset {\mathbb {N}}$ which is compatible with a tuple $(\succ _p)_{p\in P}$ of excellent orders satisfies condition (I) in Definition 2.8 (c) and in Theorem 1.4. Before, we recall some necessary definitions from [5].

Definition 2.8

[5, Definition 1.1 and Theorem 1.2] Let $M\subset {\mathbb {N}}$ be a finite non-empty set. Recall the definition of the graph (M, E(M)) in Definition 1.3.

(a) For any prime number p, the components of the graph $(M,E(M)-E_p(M))$ are called the p-planes of the graph. A p-plane is called a highest p-plane if no p-edge ends at a vertex of the p-plane. A p-edge from $m_1\in M$ to $m_2\in M$ is called a highest p-edge if no p-edge ends at $m_1$.

(b) Two properties $(T_p)$ and $(S_p)$ are defined for any prime number p:

$$\begin{aligned}&(T_p): \text {The graph }(M,E(M))\text { has only one highest }p\text {-plane}. \end{aligned}$$

(2.16)

$$\begin{aligned}&(S_p): \text {The graph }(M,E(M)-\{\text {highest }p\text {-edges}\}) \nonumber \\&\,\qquad \quad \text { has only 1 or 2 components}. \end{aligned}$$

(2.17)

(c) Condition (I) says: The graph (M, E(M)) is connected. It satisfies $(S_2)$. It satisfies $(T_p)$ for any prime number $p\ge 3$.

(d) Condition (II) says: The graph (M, E(M)) has two components $M_1$ and $M_2$. They are 2-planes. They satisfy $(T_p)$ for any prime number $p\ge 3$. Furthermore,

$$\begin{aligned} \gcd (\mathrm{lcm}(M_1),\mathrm{lcm}(M_2))\in & {} \{1,2\},\end{aligned}$$

(2.18)

$$\begin{aligned} v_2(\mathrm{lcm}(M_2))> & {} v_2(\mathrm{lcm}(M_1))\in \{0;1\}. \end{aligned}$$

(2.19)

Lemma 2.10 is new. Part (b) is used in the proof of Theorem 1.5.

Example 2.9

(i) In Remark 1.2 (ii), for $M=\{3,5\}$, it was stated $\mathrm{Aut}_{S^1}(H_M,h_M)\supsetneqq \{\pm h_M^k\,|\, k\in {\mathbb {Z}}\}\}$. By Theorem 1.4, this means that the graph (M, E(M)) satisfies neither condition (I) nor condition (II). This is true, indeed. The graph (M, E(M)) consists of the two vertices 3 and 5 and no edges. Therefore, it is is not connected, so it does not satisfy condition (I). It has the two components $\{3\}$ and $\{5\}$. They satisfy $T_p$ for each prime number $p\ge 3$, and also $\gcd (3,5)=1$. But $v_2(3)=v_2(5)=0$, so the graph (M, E(M)) does not satisfy condition (II).

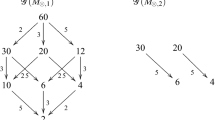
(ii) The following example is related to the isolated quasihomogeneous singularity $f=x_1(x_1^4+x_2^6)$. This will be shown in Example 6.5. Consider $M_1=\{1,3,5,15\}$ and $M_2=\{1,3,15\}\subset M_1$, so $\psi :M_1\rightarrow {\mathbb {N}}_0$ with $\psi (1)=\psi (3)=\psi (15)=2$, $\psi (5)=1$. Here ${{\mathscr {P}}}(M_1)=\{3,5\}$. The tuple $(\succ _3,\succ _5)$ of excellent orders with $s(\succ _3)=s(\succ _5)=1$ and $1\succ _3 0$, $0\succ _5 1$, is compatible with $\psi$, so with $M_1$ and $M_2$. Here are the graphs $(M_1,E_{M_1})$, $(M_2,E_{M_2})$, $(M_1,E(M_1))$ and $(M_2,E(M_2))$:

The graph $(M_1,E(M_1))$ has the highest 3-plane $\{3,15\}$ and the highest 5-plane $\{5,15\}$. The graph $(M_2,E(M_2))$ has the highest 3-plane $\{3,15\}$ and the highest 5-plane $\{15\}$. Both graphs are connected. Both satisfy $T_3$ and $T_5$. Both satisfy trivially $S_2$, because both have no 2-edges and are connected. Therefore, both satisfy condition (I).

Lemma 2.10

Let $M\subset {\mathbb {N}}$ be a finite non-empty set.

(a) $(S_p)\Longrightarrow (T_p)$ for any prime number p if the graph (M, E(M)) is connected.

(b) Let $(\succ _p)_{p\in P}$ be a tuple of excellent orders with which M is compatible. Then, the graph (M, E(M)) is connected. M satisfies $(S_p)$ for any prime number p. M satisfies condition (I).

Proof

(a) Suppose that the graph (M, E(M)) is connected and satisfies $(S_p)$, but has at least two highest p-planes. Any highest p-plane is a component of the graph $(M,E(M)-\{highest p-edges \})$. Therefore, this graph consists of exactly two highest p-planes. But then the graph (M, E(M)) has no p-edges and has the same two components, so it is not connected, a contradiction.

(b) By Lemma 2.6 (a), $(M,E_V\cap M\times M)$ is a directed subgraph of $(V,E_V)$ with center $v_V$. Therefore, it is connected. As the underlying undirected graphs of (V, E(V)) and $(V,E_V)$ coincide, also the graph (M, E(M)) is connected.

Fix a prime number p. We will prove $(S_p)$ in the next three paragraphs. Let $m_1\in M$ be arbitrary. There is a path in $(V,E_V)$ from $\pi _p(v_V)\cdot p^{v_p(m_1)}$ to $m_1$ which consists completely of edges which are not p-edges. Because of Lemma 2.6 (a) (i)$\Rightarrow$(ii), it is a path in $(M,E_V\cap M\times M)$. Therefore, the set $\{m\in M\,|\, v_p(m)=v_p(m_1)\}$ is a single p-plane in the graph (M, E(M)). Furthermore, the set $\{\pi _p(v_V)\cdot p^k\,|\, k\in K_{M,p,\pi _p(v_V)}\}$ intersects each p-plane in one element.

In particular, there is only one highest p-plane, and it intersects the set above in $\widetilde{v}_V:=\pi _p(v_V)\cdot p^{k^{(max)}}$ where $k^{(max)}:=\max (v_p(m)\,|\, m\in M)$. This highest p-plane is one component of the graph $(M,E(M)-\{highest p-edges \})$.

The edges in E(M) with both vertices in the set $\{\pi _p(v_V)\cdot p^k\,|\, k\in K_{M,p,\pi _p(v_V)}-\{k^{(max)}\}\}$ are all p-edges, but not highest p-edges. Therefore, the second component (if M does not consist only of one p-plane) is the union of all other p-planes. The property $(S_p)$ holds.

Because (M, E(M)) is connected and because of part (a), (M, E(M)) satisfies condition (I). $\square$

3 Tensor product and Thom–Sebastiani sum

The following is a reformulation of Problem 7 in [10]:

(a) Find a natural condition for a map $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ with finite support which implies that each set $M_j^{st}\subset {\mathbb {N}}$ in the standard covering of $\psi$ satisfies condition (I) and which is stable under tensor product.

(b) Prove that in the case of an isolated quasihomogeneous singularity the map $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ satisfies this condition, where $p_{ch,h_{Mil}}=\prod _{m\in {\mathbb {N}}}\varPhi _m^{\psi (m)}$ is the characteristic polynomial of the monodromy.

Problem 7 is motivated by the facts (which are discussed in [10]) that condition (I) is not stable under tensor product and that it is too difficult to prove Theorem 1.5 directly.

Here, we propose as solution the natural condition that a tuple of excellent orders exists, with which $\psi$ is compatible (Definition 2.5 (e)). The first half of part (a) is true because of Lemmas 2.10 (b) and 2.6 (b). Part (b) is true because of Theorem 6.7, which is [9, Theorem 12.1]. The second half of part (a) is also true. It follows from Theorem 3.2, which is a main result of [9]. Before, Definition 3.1 explains what is meant here by tensor product.

Definition 3.1

(a) Let $f(t)=\prod _{i=1}^n(t-\kappa _i)\in {\mathbb {C}}[t]$ and $g(t)=\prod _{j=1}^m(t-\lambda _j)\in {\mathbb {C}}[t]$ be unitary polynomials of degrees $n,m\ge 1$. Their tensor product is the unitary polynomial

$$\begin{aligned} (f\otimes g)(t):= & {} \prod _{i=1}^n\prod _{j=1}^m (t-\kappa _i\lambda _j)\in {\mathbb {C}}[t] \end{aligned}$$

(3.1)

of degree nm.

(b) Let $\psi _1:{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ and $\psi _2:{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ be two maps with finite supports $M=\mathrm{supp\, }(\psi _1)$ and $N=\mathrm{supp\, }(\psi _2)$. Their tensor product is the map $\psi _1\otimes \psi _2:{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ with

$$\begin{aligned} \Biggl (\prod _{m\in M}\varPhi _m^{\psi _1(m)}\Biggr ) \otimes \Biggl (\prod _{n\in N}\varPhi _n^{\psi _2(n)}\Biggr ) = \prod _{l\in {\mathbb {N}}}\varPhi _l^{(\psi _1\otimes \psi _2)(l)}. \end{aligned}$$

(3.2)

It has also finite support.

The beginning of Sect. 7 in [9] (namely Definition 7.1, Lemma 7.2 and Definition 7.3) gives more information on $\psi _1\otimes \psi _2$. Theorem 3.2 is a main result of [9]. The long and difficult proof is built up from several intermediate results in Sects. 7–9 in [9]. Its part (a) solves the second half of part (a) of Problem 7.

Theorem 3.2

[9, Theorem 9.10] Let $\psi _1:{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ and $\psi _2:{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ be two maps with finite supports $M=\mathrm{supp\, }(\psi _1)$ and $N=\mathrm{supp\, }(\psi _2)$. Write $\psi _3:=\psi _1\otimes \psi _2$. Denote $L:=\mathrm{supp\, }(\psi _3)$. It satisfies ${{\mathscr {P}}}(L)\subset {{\mathscr {P}}}(M)\cup {{\mathscr {P}}}(N)$.

Let $P\supset {{\mathscr {P}}}(M)\cup {{\mathscr {P}}}(N)$ be a finite set of prime numbers. Let $(\succ _p^M)_{p\in P}$ and $(\succ _p^N)_{p\in P}$ be two tuples of excellent orders such that $\psi _1$ is compatible with $(\succ _p^M)_{p\in P}$ and $\psi _2$ is compatible with $(\succ _p^N)_{p\in P}$. Write $\succ _p^L:=(\succ _p^M\otimes \succ _p^N)$ for any $p\in P$.

(a) $\psi _3$ is compatible with the tuple $(\succ _p^L)_{p\in P}$ of excellent orders.

(b) Let $(M_1^{(st)},\ldots ,M_{l_{\psi _1}}^{(st)})$, $(N_1^{(st)},\ldots ,N_{l_{\psi _2}}^{(st)})$ and $(L_1^{(st)},\ldots ,L_{l_{\psi _3}}^{(st)})$ be the standard coverings of $\psi _1$, $\psi _2$ and $\psi _3$. Then,

$$\begin{aligned} \Biggl (\bigoplus _{i=1}^{l_{\psi _1}}\mathrm{Or}(M_i^{(st)})\Biggr ) \otimes \Biggl (\bigoplus _{j=1}^{l_{\psi _2}}\mathrm{Or}(N_j^{(st)})\Biggr ) \cong \bigoplus _{k=1}^{l_{\psi _3}}\mathrm{Or}(L_k^{(st)}), \end{aligned}$$

(3.3)

so the tensor product of the sums of Orlik blocks on the left hand side admits a standard decomposition into Orlik blocks.

Example 3.3

Here, two examples are given, where the hypotheses and the conclusions in Theorem 3.2 are not satisfied. In the examples, we write $H_M$ instead of the pair $(H_M,h_M)$.

(i) Consider $M=\{3\}$ and $N=\{2,3\}$. Then, the following is shown in [9, Example 7.7. (iii)].

$$\begin{aligned} H_{\{3\}}\otimes H_{\{2,3\}}\cong H_{\{3,1\}}\oplus H_{\{6,1\}}\not \cong H_{\{6,3,1\}}\oplus H_{\{1\}}. \end{aligned}$$

(3.4)

So, here the tensor product $H_{\{3\}}\otimes H_{\{2,3\}}$ is isomorphic to a direct sum of Orlik blocks, but not to a standard decomposition into Orlik blocks. The set $M=\{3\}$ is compatible with the excellent order $\succ ^M_3$ on the set $\{0,1\}$ with $1\succ ^M_30$. But there is no tuple $(\succ ^N_2,\succ ^N_3)$ of excellent orders on $\{0,1\}$ which is compatible with the set $N=\{2,3\}$: Else by Lemma 2.10, the graph (N, E(N)) would be connected which it is not.

(ii) Similarly to the example in (iii), one can show

$$\begin{aligned} H_{\{4\}}\otimes (H_{\{4,1\}}\oplus H_{\{1\}}) \cong H_{\{4,2,1\}}\oplus H_{\{2,1\}}\oplus H_{\{4\}} \not \cong H_{\{4,2,1\}}\oplus H_{\{4,2,1\}}. \end{aligned}$$

(3.5)

So, also here the tensor product is isomorphic to a direct sum of Orlik blocks, but not to a standard decomposition into Orlik blocks. Here,

$$\begin{aligned} M= & {} \{4\},\ \psi _1(4)=1,\quad N=\{1,4\},\ \psi _2(1)=2,\ \psi _2(4)=1, \nonumber \\ L= & {} \{1,2,4\},\ \psi _3(1)=\psi _3(2)=\psi _3(4)=2. \end{aligned}$$

(3.6)

The set $M=\{4\}$ is compatible with the excellent order $\succ _2^M$ on the set $\{0,1,2\}$ with $2\succ _2^M 1\succ _2^M 0$. But the map $\psi _2$ is not compatible with any excellent order $\succ _2^N$ on the set $\{0,1,2\}$: Because the set $N=\{1,4\}$ and the set $\{1\}$ must be compatible with $\succ _2^N$, we must have $0\succ _2^N 2$. Now the compatibility of N with $\succ _2^N$ requires $0\succ _2^N 2\succ _2^N 1$. But this is not an excellent order on $\{0,1,2\}$.

Thom and Sebastiani proved a result which specializes to the case of isolated quasihomogeneous singularities as follows.

Theorem 3.4

[21] Let $f=f(x_1,\ldots ,x_{n_f})$ and $g=g(x_{n_f+1},\ldots ,x_{n_f+n_g})$ be two isolated quasihomogeneous singularities in different variables. Then, their Thom–Sebastiani sum $f+g$ is an isolated quasihomogeneous singularity, and there is a canonical isomorphism

$$\begin{aligned} (H_{Mil},h_{Mil})(f+g)\cong (H_{Mil},h_{Mil})(f)\otimes (H_{Mil},h_{Mil})(g). \end{aligned}$$

(3.7)

This theorem, Theorem 6.7 and part (b) of Theorem 3.2, implies part (c) of Theorem 1.7. This is the way how Theorem 1.7 (c) is proved in [9].

Remark 3.5

The search for Theorem 3.2 led us in the following way to the excellent orders and the compatibility of a finite set $M\subset {\mathbb {N}}$ with a tuple of excellent orders. We found a condition sdiOb-sufficient [9, Definition 7.3 (d)] (short for standard decomposition into Orlik blocks) for a pair (M, N) of finite subsets $M,N\subset {\mathbb {N}}$ which implies (and probably is equivalent to) the property that the tensor product $(H_M,h_M)\otimes (H_N,h_N)$ of two Orlik blocks allows a standard decomposition into Orlik blocks [9, Theorem 7.4]. Lemma 9.12 in [9] says especially that the following conditions (i) and (ii) are equivalent. Here, $M\subset {\mathbb {N}}$ is a finite non-empty set.

• (i) For any $n_N\in {\mathbb {N}}$, the pair $(M,\{n\in {\mathbb {N}}\,|\, n|n_N\})$ is sdiOb-sufficient.

• (ii) A tuple $(\succ _p)_{p\in {{\mathscr {P}}}(M)}$ of excellent orders exists such that M is compatible with it.

Another interesting result from [9] which complements Theorem 3.2 (and which, in fact, is used in its proof) is the following.

Theorem 3.6

[9, Theorem 9.6] Let $(\succ _p)_{p\in P}$ be at tuple of excellent orders for a finite set P of prime numbers, and let $\psi :{\mathbb {N}}\rightarrow {\mathbb {N}}_0$ be a map with finite support which is compatible with $(\succ _p)_{p\in P}$. Let $(M_1^{(1)},\ldots ,M_{l_1}^{(1)}))$ and $(M_1^{(2)},\ldots , M_{l_2}^{(2)})$ be two coverings of $\psi$ which are both compatible with $(\succ _p)_{p\in P}$. Then, the corresponding sums of Orlik blocks are isomorphic,

$$\begin{aligned} \bigoplus _{i=1}^{l_1}\mathrm{Or}(M_i^{(1)})\cong & {} \bigoplus _{j=1}^{l_2}\mathrm{Or}(M_j^{(2)}), \end{aligned}$$

(3.8)

and $l_1=l_2=l_\psi (:=\max (\psi (m)\,|\, m\in {\mathbb {N}}))$.

4 Maps on the group ring generated by unit roots

This section collects notations and classical formulas which will be needed in the later sections.

Notations 4.1

(a)Denote by $\mu ({\mathbb {C}})\subset S^1$ the group of all unit roots. Denote by ${\mathbb {Q}}[\mu ({\mathbb {C}})]$ and ${\mathbb {Z}}[\mu ({\mathbb {C}})]$ the group rings of elements $\sum _{j=1}^lb_j[\zeta _j]$ where $\zeta _j\in \mu ({\mathbb {C}})$ and where $b_j\in {\mathbb {Q}}$ respectively ${\mathbb {Z}}$, with multiplication $[\zeta _1][\zeta _2]=[\zeta _1\zeta _2]$. The unit element is [1]. The trace and the degree of an element $b=\sum _{j=1}^lb_j[\zeta _j]\in {\mathbb {Q}}[\mu ({\mathbb {C}})]$ are

$$\begin{aligned} \mathrm{tr}(b):=\sum _{j=1}^lb_j\zeta _j\in {\mathbb {C}},\quad \deg (b):=\sum _{j=1}^lb_j\in {\mathbb {Q}}. \end{aligned}$$

The trace map $\mathrm{tr}:{\mathbb {Q}}[\mu ({\mathbb {C}})]\rightarrow {\mathbb {C}}$ and the degree map $\deg :{\mathbb {Q}}[\mu ({\mathbb {C}})]\rightarrow {\mathbb {Q}}$ are ring homomorphisms. For $k\in {\mathbb {N}}_0$, the k-th Lefschetz number $L_k(b)$ of an element $b=\sum _{j=1}^lb_j[\zeta _j]$ is

$$\begin{aligned} L_k(b):=\sum _{j=1}^lb_j\zeta _j^k =\mathrm{tr}\left( \sum _{j=1}b_j[\zeta _j^k]\right) \in {\mathbb {C}}. \end{aligned}$$

(4.1)

(b) The divisor of a unitary polynomial $f=\prod _{i=1}^n(t-\kappa _i)$ with $\kappa _i\in \mu ({\mathbb {C}})$ is

$$\begin{aligned} \mathrm{div\, }f:=\sum _{i=1}^n[\kappa _i]\in {\mathbb {Z}}[\mu ({\mathbb {C}})]. \end{aligned}$$

The divisor of the constant polynomial 1 is $\mathrm{div\, }1=0$.

(c) The order $\mathrm{ord\, }(\zeta )\in {\mathbb {N}}$ of a unit root $\zeta \in \mu ({\mathbb {C}})$ is the minimal number $m\in {\mathbb {N}}$ with $\zeta ^m=1$. For $m\in {\mathbb {N}}$, the m-th cyclotomic polynomial is

$$\begin{aligned} \varPhi _m:=\prod _{\zeta :\,\mathrm{ord\, }(\zeta )=m}(t-\zeta ). \end{aligned}$$

Define

$$\begin{aligned} \varLambda _m:=\mathrm{div\, }(t^m-1),\quad \varPsi _m:=\mathrm{div\, }\varPhi _m. \end{aligned}$$

(4.2)

Then, $\lambda _1=\varPsi _1=[1]$. The Möbius function $\mu _{Moeb}$ is [1]

$$\begin{aligned} \mu _{Moeb}:{\mathbb {N}}\rightarrow & {} \{0,1,-1\},\\ m\mapsto & {} \left\{ \begin{array}{ll} (-1)^r &{} \quad if m=p_1\cdot \ldots \cdot p_r with p_1,\ldots ,p_r\\ &{}\quad different prime numbers ,\\ 0&{}\quad else \end{array}\right. \end{aligned}$$

(here $r=0$ is allowed, so $\mu _{Moeb}(1)=1$).

The next lemma collects well-known facts.

Lemma 4.2

(a) Let $f=\prod _{i=1}^n(t-\kappa _i)$ and $g=\prod _{j=1}^m(t-\lambda _j)$ be unitary polynomials with $\kappa _i$ and $\lambda _j\in \mu ({\mathbb {C}})$. The tensor product $(f\otimes g)(t)=\prod _{i=1}^n\prod _{j=1}^m (t-\kappa _i\lambda _j)$ in (3.1) satisfies

$$\begin{aligned} \mathrm{div\, }(f\otimes g) =(\mathrm{div\, }f)\cdot (\mathrm{div\, }g). \end{aligned}$$

(b) The cyclotomic polynomial $\varPhi _m$ is in ${\mathbb {Z}}[t]$, it has degree $\varphi (m)$, and it is irreducible in ${\mathbb {Z}}[t]$ and ${\mathbb {Q}}[t]$.

$$\begin{aligned} t^n-1= & {} \prod _{m|n}\varPhi _m(t),\qquad \varLambda _n=\sum _{m|n}\varPsi _m, \end{aligned}$$

(4.3)

$$\begin{aligned} \varPhi _m= & {} \prod _{m|n}(t^n-1)^{\mu _{Moeb}\left( \frac{m}{n}\right) },\quad \varPsi _m=\sum _{n|m}\mu _{Moeb}\left( \frac{m}{n}\right) \cdot \varLambda _n. \end{aligned}$$

(4.4)

The traces of $\varLambda _m$ and $\varPsi _m$ are

$$\begin{aligned} \mathrm{tr}\varLambda _m= & {} \left\{ \begin{array}{ll} 1&{}\quad if m=1\\ 0&{}\quad if m\ge 2,\end{array}\right. \end{aligned}$$

(4.5)

$$\begin{aligned} \mathrm{tr}\varPsi _m= & {} \mu _{Moeb}(m). \end{aligned}$$

(4.6)

The product $\varLambda _m\varLambda _n$ is

$$\begin{aligned} \varLambda _m \varLambda _n= & {} \gcd (m,n)\cdot \varLambda _{\mathrm{lcm}(m,n)}. \end{aligned}$$

(4.7)

For the product $\varPsi _m\varPsi _n$, see [10, (2.19)–(2.21)] or [9, Lemma 7.2].

(c) Let $\psi :{\mathbb {N}}\rightarrow {\mathbb {Q}}$ be a map with finite support, and consider the element

$$\begin{aligned} b:=\sum _{m\in {\mathbb {N}}}\psi (m)\cdot \varPsi _m\in {\mathbb {Q}}[\mu ({\mathbb {C}})]. \end{aligned}$$

(4.8)

There is a unique map $\chi :{\mathbb {N}}\rightarrow {\mathbb {Q}}$ with finite support and

$$\begin{aligned} b=\sum _{n\in {\mathbb {N}}}\chi (n)\cdot \varLambda _n. \end{aligned}$$

(4.9)

The four data $\psi$, b, $\chi$ and $(L_k(b))_{k\in {\mathbb {N}}_0}$ determine one another, by (4.8)–(4.9) and

$$\begin{aligned} \psi (m)=\sum _{n:\, m|n}\chi (n),\quad \chi (n)=\sum _{m:\, n|m}\psi (m)\cdot \mu _{Moeb} \left( \frac{m}{n}\right) , \end{aligned}$$

(4.10)

$$\begin{aligned} L_k(b)= \sum _{n:\, n|k}n\chi (n),\quad n\chi (n)=\sum _{k|n}L_k(b)\cdot \mu _{Moeb}\left( \frac{n}{k}\right) . \end{aligned}$$

(4.11)

Denote $d_\chi :=\mathrm{lcm}(n\,|\, n\in \mathrm{supp\, }(\chi ))$. The Lefschetz numbers $L_k(b)$ are rational. They are determined by the values $L_k(b)$ for $k\in {\mathbb {N}}$ with $k| d_\chi$, because of the (extended) periodicity property

$$\begin{aligned} L_k(b)=L_{\gcd (k,d_\chi )}(b)\qquad for any k\in {\mathbb {N}}. \end{aligned}$$

(4.12)

Proof

(a) Trivial. (b) The statements on $\varPhi _m$ are classical. The formulas (4.4) follow from the formulas (4.3) by Moebius inversion [1]. The trace of $\varLambda _m$ is obvious, the trace of $\varPsi _m$ follows with (4.4). The product $\varLambda _m\varLambda _n$ is obvious.

(c) Formula (4.10) is a consequence of (4.3) and (4.4). The first formula in (4.11) can be seen as follows:

$$\begin{aligned} L_k(\varLambda _n)= & {} \mathrm{tr}\left( \sum _{a=0}^{n-1}[e^{2\pi i ak/n}]\right) \\= & {} \mathrm{tr}\left( \gcd (k,n)\varLambda _{n/\gcd (k,n)}\right) =\left\{ \begin{array}{ll} n&{}\quad if n|k,\\ 0&{}\quad if n\not | k,\end{array} \right. \\ L_k(b)= & {} \sum _{n\in {\mathbb {N}}}\chi (n)\cdot L_k(\varLambda _n) =\sum _{n:\, n|k}n\chi (n). \end{aligned}$$

The first formula in (4.11) gives the second formula in (4.11) by Moebius inversion [1]. It also implies $L_k(b)\in {\mathbb {Q}}$ and the periodicity property (4.12). $\square$

5 Basic properties of weight systems and induced objects

In this section, problem 1 in [10] will be solved as part of Lemma 5.4. It is elementary. Before, notations from [10,  Sect. 3] are recalled. In this section, we fix a number $n\in {\mathbb {N}}$ and denote $N:=\{1,2,\ldots ,n\}$.

Definition 5.1

(a) A weight system is a tuple $(v_1,\ldots ,v_n;d)\in ({\mathbb {Q}}_{>0})^{n+1}$ with $v_i<d$. Another weight system is equivalent, if the second one has the form $q\cdot (v_1,\ldots ,v_n;d)$ for some $q\in {\mathbb {Q}}_{>0}$. A weight system is integer if $(v_1,\ldots ,v_n;d)\in {\mathbb {N}}^{n+1}$. It is reduced if it is integer and $\gcd (v_1,\ldots ,v_n,d)=1$. It is normalized if $d=1$.

Any equivalence class contains a unique reduced weight system and a unique normalized weight system. From now on, the letters $(v_1,\ldots ,v_n;d)$ will be reserved for an integer weight system, and the letters $(w_1,\ldots ,w_n;1)$ will be the equivalent normalized weight system, i.e., $w_i=v_i/d$.

(b) Let $(v_1,\ldots ,v_n;d)$ be an integer weight system (not necessarily reduced). For $J\subset N$ and $k\in {\mathbb {N}}_0$ define

$$\begin{aligned} ({\mathbb {Z}}^J)_k:= & {} \left\{ \alpha \in {\mathbb {Z}}^n\,|\, \alpha _i=0\text { for } i\notin J,\ \sum _{i\in J}\alpha _i=k\right\} ,\nonumber \\ ({\mathbb {N}}_0^J)_k:= & {} {\mathbb {N}}_0^n\cap ({\mathbb {Z}}^J)_k. \end{aligned}$$

(5.1)

(c) Two conditions for an integer weight system $(v_1,\ldots ,v_n;d)$ (or, equivalently, for the equivalent normalized weight system $(\frac{v_1}{d},\ldots , \frac{v_n}{d};1)$) are defined as follows:

$$\begin{aligned} \overline{(C2)}:&\forall \ J\subset N\text { with }J\ne \emptyset \quad \exists \ K\subset N \text { with }|K|=|J|\\&\,\, \text {and such that } \forall \ k\in K\text { we have }({\mathbb {Z}}^J)_{d-v_k}\ne \emptyset .\\ (C2):&\forall \ J\subset N\text { with }J\ne \emptyset \quad \exists \ K\subset N \text { with }|K|=|J|\\&\,\, \text {and such that } \forall \ k\in K\text { we have }({\mathbb {N}}_0^J)_{d-v_k}\ne \emptyset . \end{aligned}$$

Remark 5.2

(i) Often for a given set J, the set $\{k\in N\,|\, ({\mathbb {N}}_0^J)_{d-v_k}\ne \emptyset \}$ has more elements than J. Then, the set K in (C2) is not unique. If for at least one J, this set has less elements than J, then (C2) does not hold. The same is true for condition $\overline{(C2)}$.

(ii) Of course (C2) implies $\overline{(C2)}$. Lemma 2.1 in [7] gives four conditions (C1), $(C1)'$, $(C2)'$ and (C3) which are equivalent to (C2). They all have versions $\overline{(C1)}$, $\overline{(C1)'}$, $\overline{(C2)'}$ and $\overline{(C3)}$, which are equivalent to $\overline{(C2)}$. Theorem 6.1 shows the relevance of (C2).

(iii) Let $(v_1,\ldots ,v_n;d)$ be an integer weight system. For $J\subset N$ with $J\ne \emptyset$ define the semigroup

$$\begin{aligned} SG(J):= & {} \sum _{j\in J}{\mathbb {N}}_0\cdot v_j\subset {\mathbb {N}}_0, \end{aligned}$$

and observe $\sum _{j\in J}{\mathbb {Z}}\cdot v_j={\mathbb {Z}}\cdot \gcd (v_j\,|\, j\in J)$. Therefore,

$$\begin{aligned} ({\mathbb {N}}_0^J)_k\ne \emptyset\iff & {} k\in SG(J), \end{aligned}$$

(5.2)

$$\begin{aligned} ({\mathbb {Z}}^J)_k\ne \emptyset\iff & {} \gcd (v_j\,|\, j\in J)|k. \end{aligned}$$

(5.3)

$\overline{(C2)}$ is equivalent to the condition

$$\begin{aligned} (GCD)&\forall \ J\subset N\ \gcd (v_j\,|\, j\in J) \text { divides at least }|J|\\&\text {of the numbers }d-v_k\text { for }k\in N. \end{aligned}$$

Definition 5.3

Let $(\mathbf{v},d)=(v_1,\ldots ,v_n,d)\in {\mathbb {N}}^{n+1}$ be an integer weight system.

(a) Define unique numbers $s_1,\ldots ,s_n,t_1,\ldots ,t_n\in {\mathbb {N}}$ by

$$\begin{aligned}&\frac{v_i}{d}=\frac{s_i}{t_i}\quad \text {and}\quad \gcd (s_i,t_i)=1. \end{aligned}$$

(5.4)

They depend only on the normalized weight system $\mathbf{w}=(w_1,\ldots w_n)=(\frac{v_1}{d},\ldots ,\frac{v_n}{d})$. Define

$$\begin{aligned}&d_\mathbf{w}:=\mathrm{lcm}(t_j\, |\, j\in N). \end{aligned}$$

(5.5)

Of course $d_\mathbf{w}|d$. If $(\mathbf{v},d)$ is reduced and $\gcd (v_1,\ldots ,v_n)|d$ (which holds for example if $\overline{(C2)}$ holds), then $\gcd (v_1,\ldots ,v_n)=1$ and then $d_\mathbf{w}=d$.

(b) For $k\in {\mathbb {N}}$ define

$$\begin{aligned} M(k):= & {} \{j\in N\, |\, t_j|k\}, \end{aligned}$$

(5.6)

$$\begin{aligned} \text {and }\mu (k):= & {} \prod _{j\in M(k)}\left( \frac{1}{w_j}-1\right) =\prod _{j\in M(k)}\frac{d-v_j}{v_j}\in {\mathbb {Q}}_{>0} \end{aligned}$$

(5.7)

(By definition, the empty product has value 1).

(c) Define a quotient of polynomials

$$\begin{aligned} \rho _{(\mathbf{v},d)}(t):= & {} t^{v_1+\cdots +v_n}\cdot \prod _{j=1}^n \frac{t^{d-v_j}-1}{t^{v_j}-1} \in {\mathbb {Q}}(t) \end{aligned}$$

(5.8)

and an element of ${\mathbb {Q}}[\mu ({\mathbb {C}})]$

$$\begin{aligned} D_\mathbf{w}:= & {} \prod _{j=1}^n \left( \frac{1}{s_j}\varLambda _{t_j}-\varLambda _1\right) \in {\mathbb {Q}}[\mu ({\mathbb {C}})]. \end{aligned}$$

(5.9)

Lemma 5.4

([10, Lemma 3.7] for (a)–(c)) Let $(\mathbf{v};d)=(v_1,\ldots ,v_n;d)\in {\mathbb {N}}^{n+1}$ be an integer weight system.

(a) Then, $M(k)=M(\gcd (k,d_\mathbf{w}))$ and $\mu (k)=\mu (\gcd (k,d_\mathbf{w}))$.

(b) The Lefschetz numbers $L_k(D_\mathbf{w})$ are

$$\begin{aligned} L_k(D_\mathbf{w})= & {} (-1)^{n-|M(k)|}\mu (k) \end{aligned}$$

(5.10)

$$\begin{aligned}= & {} L_{\gcd (k,d_\mathbf{w})}(D_\mathbf{w}). \end{aligned}$$

(5.11)

(c) $(\mathbf{v};d)$ satisfies $\overline{(C2)}\iff \rho _{(\mathbf{v};d)}\in {\mathbb {Z}}[t]$.

(d) Suppose that $(\mathbf{v};d)$ satisfies $\overline{(C2)}$. Write

$$\begin{aligned} \rho _{(\mathbf{v};d)}=\sum _{\alpha \in d^{-1}{\mathbb {N}}_0} \sigma (\alpha )\cdot t^{d\cdot \alpha } \end{aligned}$$

with a unique map $\sigma :d^{-1}{\mathbb {N}}_0\rightarrow {\mathbb {Z}}$ with finite support. Then,

$$\begin{aligned} D_\mathbf{w}= & {} \sum _{\alpha \in d^{-1}{\mathbb {N}}_0} \sigma (\alpha )\cdot [e^{2\pi i \alpha }]. \end{aligned}$$

(5.12)

and $\mu (k)\in {\mathbb {N}}$.

Proof

(a) All $t_j$ divide $d_\mathbf{w}$. Therefore, $t_j|k\iff t_j|\gcd (k,d_\mathbf{w})$.

(b) For completeness sake, the calculation in [10] is copied.

$$\begin{aligned} L_k(D_\mathbf{w})= & {} \mathrm{tr}\left( \prod _{j=1}^n \left( \frac{\gcd (k,t_j)}{s_j} \varLambda _{t_j/\gcd (k,t_j)}-\varLambda _1\right) \right) \\= & {} \prod _{j=1}^n \left( \frac{\gcd (k,t_j)}{s_j}\cdot \mathrm{tr}\left( \varLambda _{t_j/\gcd (k,t_j)}\right) -1\right) \\= & {} \prod _{j\in M(k)}\left( \frac{t_j}{s_j}-1\right) \cdot \prod _{j\notin M(k)}(-1)\\= & {} (-1)^{n-|M(k)|}\cdot \mu (k). \end{aligned}$$

Formula (5.11) follows from part (a).

(c) The conditions $\overline{(C2)}$ and (GCD) in Remark 5.2 (iii) are equivalent. Condition (GCD) says that any cyclotomic polynomial in the denominator of $\rho _{(\mathbf{v};d)}$ turns up with at least the same multiplicity in the numerator. Therefore, (GCD) is equivalent to $\rho _{(\mathbf{v};d)}\in {\mathbb {Z}}[t]$.

(d) The formulas (5.10) and (5.12) imply $\mu (k)\in {\mathbb {N}}$. For (5.12), it is because of Lemma 4.2 (c) sufficient to show

$$\begin{aligned} L_k(D_\mathbf{w})= & {} L_k\left( \sum _{\alpha \in d^{-1}{\mathbb {N}}_0} \sigma (\alpha )\cdot [e^{2\pi i\alpha }]\right) \quad for all k\in {\mathbb {N}}_0. \end{aligned}$$

(5.13)

The right-hand side of (5.13) is

$$\begin{aligned}&\mathrm{tr}\left( \sum _{\alpha \in d^{-1}{\mathbb {N}}_0} \sigma (\alpha )\cdot [e^{2\pi ik\alpha }]\right) = \sum _{\alpha \in d^{-1}{\mathbb {N}}_0} \sigma (\alpha )\cdot e^{2\pi ik\alpha } = \rho _{(\mathbf{v};d)}(e^{2\pi i k/d})\\&\quad = \lim _{t\mapsto e^{2\pi i k/d}} \left( \prod _{j\in M(k)}\frac{t^d-t^{v_j}}{t^{v_j}-1} \cdot \prod _{j\notin M(k)}\frac{t^d-t^{v_j}}{t^{v_j}-1} \right) \\&\quad = \left( \prod _{j\in M(k)}\frac{d-v_j}{v_j}\right) \cdot (-1)^{n-|M(k)|} =(-1)^{n-|M(k)|}\mu (k) =L_k(D_\mathbf{w}). \end{aligned}$$

Here, we used $j\notin M(k)\iff \frac{k}{d}v_j\notin {\mathbb {Z}}\iff (e^{2\pi i k/d})^{v_j}\ne 1$. $\square$

Remark 5.5

Problem 1 in [10] asked whether (5.12) holds. In [10], the first author had missed the calculation in the proof of part (d).

6 Isolated quasihomogeneous singularities

Finally, we come to the discussion of weight systems which allow isolated quasihomogeneous singularities and of associated objects. The following Theorems 6.1 and 6.4 are crucial. As in Sect. 5, $n\in {\mathbb {N}}$ and $N=\{1,\ldots ,n\}$ are fixed.

Theorem 6.1

(Kouchnirenko [11,  Remarque 1.13 (ii)]) Let $(\mathbf{v};d)=(v_1,\ldots ,v_n;d)$ be an integer weight system. The following conditions are equivalent.

• (IS3): There exists a quasihomogeneous polynomial f with weight system $(\mathbf{v};d)$ and an isolated singularity at 0.

• (IS3)’: A generic quasihomogeneous polynomial with weight system $(\mathbf{v};d)$ has an isolated singularity at 0.

• (C2): The weight system $(\mathbf{v};d)$ satisfies condition (C2).

Remark 6.2

(i) The reference [11,  Remarque 1.13 (ii)] does not give a detailed proof, but the reference [12] (in russian) does. The theorem was rediscovered and reproved several times, in [13, 17] and [3]. More general results are given in [22] (without proof) and [25] (with proof). The paper [7] discussed the history of Theorem 6.1, but it missed the reference [3].

(ii) Lemma 2.1 in [7] shows combinatorially the equivalence of (C2) with several other conditions (C1), (C1)’, (C2)’ and (C3). Some of the references above prove the equivalence of (IS3) with some other of these conditions.

(iii) The implication (IS3)$\Rightarrow$(C1) is already shown in [18].

Remark 6.3

The paper [7] made good use of the part of condition (C2) which concerns subsets $J\subset N$ with $|J|=1$. Problem 3 in [10] asked about making good use of the conditions in (C2) for sets $J\subset N$ with $|J|\ge 2$. Of course, the proofs of Theorem 6.1 in the references in Remark 6.2 (i) make such good use, as they need the full condition (C2). We do not have other solutions of problem 3 in [10].

Theorem 6.4

Let $(\mathbf{v};d)=(v_1,\ldots ,v_n;d)$ be an integer weight system which satisfies condition (C2), and let $\mathbf{w}=(\frac{v_1}{d},\ldots ,\frac{v_n}{d};1)$ be the equivalent normalized weight system.

(a) (Milnor and Orlik [15]) $D_\mathbf{w}$ is the divisor of the characteristic polynomial of the monodromy on the Milnor lattice of an isolated quasihomogeneous singularity with weight system $(\mathbf{v};d)$. In particular, $D_\mathbf{w}\in {\mathbb {N}}_0[\mu ({\mathbb {C}})]$.

(b) (Many people, e.g., [2]) $t^{-v_1-\ldots -v_n}\rho _{(\mathbf{v};d)}$ is the generating function of the weighted degrees of the Jacobi algebra

$$\begin{aligned} {\mathbb {C}}[x_1,\ldots ,x_n]/\Bigl (\frac{\partial f}{\partial x_1},\ldots , \frac{\partial f}{\partial x_n}\Bigr ) \end{aligned}$$

of an isolated quasihomogeneous singularity f with weight system $(\mathbf{v};d)$. Especially $\rho _{(\mathbf{v};d)}\in {\mathbb {N}}_0[t]$.

Example 6.5

The polynomial $f(x_1,x_0)=x_1(x_1^4+x_2^6)$ is an isolated quasihomogeneous singularity with normalized weight system $\mathbf{w}=(w_1,w_2;1)=(\frac{1}{5},\frac{2}{15};1)$. In particular, $(s_1,t_1,s_2,t_2)=(1,5,2,15)$. The divisor of the characteristic polynomial of its monodromy is

$$\begin{aligned} D_\mathbf{w}= & {} \bigl (\varLambda _5-\varLambda _1\bigr ) \bigl (\frac{1}{2}\varLambda _{15}-\varLambda _1\bigr )\\= & {} 2\varLambda _{15}-\varLambda _5+\varLambda _1 =2\varPsi _{15}+\varPsi _5+2\varPsi _3+2\varPsi _1, \end{aligned}$$

so here $p_{ch,Mil}=\prod _{m\in M_1}\varPhi _m^{\psi (m)}$ with $M_1=\{1,3,5,15\}$ and $\psi (15)=\psi (3)=\psi (1)=2$, $\psi (5)=1$. The standard covering (Definition 2.5 (f)) of $\psi$ consists of $M_1$ and $M_2=\{1,3,15\}\subset M_1$. Theorem 6.7 shows here that $\psi$ and $M_1$ and $M_2$ are compatible with the tuple $(\succ _3^\mathbf{w},\succ _5^\mathbf{w})$, where $s(\succ _3^\mathbf{w})=1=s(\succ _5^\mathbf{w})$ and $1\succ _3^\mathbf{w}0$, $0\succ _5^\mathbf{w}1$. We had observed this already in Example 2.9.

Remark 6.6

(i) By Lemma 5.4 (d), $\rho _{(\mathbf{v};d)}$ and $D_\mathbf{w}$ are related by

$$\begin{aligned} \rho _{(\mathbf{v};d)}=\sum _{\alpha \in d^{-1}{\mathbb {N}}_0}\sigma (\alpha ) \cdot t^{d\cdot \alpha },\qquad D_\mathbf{w}=\sum _{\alpha \in d^{-1}{\mathbb {N}}_0}\sigma (\alpha )\cdot [e^{2\pi i \alpha }], \end{aligned}$$

(6.1)

where $\sigma :d^{-1}{\mathbb {N}}_0\rightarrow {\mathbb {N}}_0$ has finite support.

(ii) If we write $\rho _{(\mathbf{v};d)}=\sum _{i=1}^\mu t^{d\cdot \alpha _i}$ for suitable $\alpha _i\in {\mathbb {Q}}$, then these numbers $(\alpha _1,\ldots ,\alpha _\mu )$ are the exponents of the singularity, and $e^{2\pi i\alpha _1},\ldots ,e^{2\pi i\alpha _\mu }$ are the eigenvalues of the monodromy.

(iii) Problem 2 in [10] asked for a combinatorial proof of the fact $\rho _{(\mathbf{v};d)}\in {\mathbb {N}}_0[t]$ for a weight system $(\mathbf{v};d)$ with condition (C2). (The other two parts of Problem 2 in [10] would follow from this and from Lemma 5.4 (d).) Theorem 6.4 (b), which was rediscovered by many people, contains this statement. The classical proof uses that the tuple of partial derivatives $(\frac{\partial f}{\partial x_1},\ldots ,\frac{\partial f}{\partial x_n})$ is a regular sequence. We do not know a proof which does not use the Jacobi algebra and this regular sequence. So we do not have a solution of problem 2 in [10].

The following theorem is proved in [9]. It is one ingredient of the proof in [9] of Theorem 1.7 (c). It is also an ingredient in the proof of Theorem 1.5. Its proof in [9] uses Theorems 6.1 and 6.4 (a) and especially that certain subsystems $\mathbf{w}^{(p)}$ of $\mathbf{w}$ (for certain prime numbers p) also satisfy condition (C2) and thus that $D_{\mathbf{w}^{(p)}}\in {\mathbb {N}}_0[\mu ({\mathbb {C}})]$ holds.

Theorem 6.7

Consider a normalized weight system $\mathbf{w}=(w_1,\ldots ,w_n;1)$ which satisfies condition (C2), and consider the numbers $s_i,t_i\in {\mathbb {N}}$ with $w_i=\frac{s_i}{t_i}$ and $\gcd (s_i,t_i)=1$. Write $D_\mathbf{w}=\sum _{m\in M_\mathbf{w}} \psi _\mathbf{w}(m)\cdot \varPsi _m$ where the map $\psi _\mathbf{w}:M_\mathbf{w}\rightarrow {\mathbb {N}}_0$ has finite support $M_\mathbf{w}\subset {\mathbb {N}}$. The map $\psi _\mathbf{w}$ is compatible with the tuple $(\succ _p^\mathbf{w})_{p\in {{\mathscr {P}}}(M_\mathbf{w})}$ of excellent orders which is defined as follows:

$$\begin{aligned} s(\succ _p^\mathbf{w}):= & {} \max (v_p(m)\,|\, m\in M_\mathbf{w}), \end{aligned}$$

(6.2)

$$\begin{aligned} S(\succ _p^\mathbf{w}):= & {} \{k\in {\mathbb {Z}}_{[1,s(\succ _p)]}\,|\, |\{j\in N\,|\, p^k|t_j\}|\text { is odd.}\} \end{aligned}$$

(6.3)

Finally, we solve problem 4 in [10] in Remark 6.9 and discuss problem 5 in [10] in Remark 6.10.

Remark 6.8

An isolated quasihomogeneous singularity $f\in {\mathbb {C}}[x_1,\ldots ,x_n]$ has multiplicity $\ge 3$ if all monomials in it have degree $\ge 3$ (the standard degree, not the weighted degree). A result in [18] says first that the weight system $\mathbf{w}$ of any isolated quasihomogeneous singularity with multiplicity $\ge 3$ is unique and satisfies $w_i\in (0,\frac{1}{2})$ for all i, and second that any quasihomogeneous singularity can be transformed by a coordinate change to a Thom–Sebastiani sum $f(x_1,\ldots ,x_k)+x_{k+1}^2+\cdots +x_n^2$ of an isolated quasihomogeneous singularity f of multiplicity $\ge 3$ and the $A_1$-singularity $x_{k+1}^2+\cdots +x_n^2$. Because of Theorem 3.4, one can often restrict to (isolated quasihomogeneous) singularities of multiplicity $\ge 3$.

Remark 6.9

Let f be an isolated quasihomogeneous singularity of multiplicity $\ge 3$ with weight system $\mathbf{w}=(w_1,\ldots ,w_n;1)$. If $n\le 3$, $(C2)\iff \overline{(C2)}$. This was first proved in [19, Theorem 3]. A short combinatorial proof is given in [7, Lemma 2.5]. For $n\ge 4$, (C2) is stronger than $\overline{(C2)}$. Though only one weight system $\mathbf{w}$ with $n=4$ which satisfies $\overline{(C2)}$, but not (C2), is published, the weight system (58, 33, 24, 1; 265). It is due to Ivlev [2]. It is also discussed in [10, Example 5.1]. There problem 4 is posed. It asks for other weight systems $\mathbf{w}$ with $n=4$ which satisfy $\overline{(C2)}$, but not (C2).

We used the software PARI/GP [23] in order to check all reduced integer weight systems $(\mathbf{v};d)=(v_1,v_2,v_3,v_4;d)$ with $\frac{d}{2}>v_1\ge v_2\ge v_3\ge v_4$ and $d\le 360$ (reduced means $\gcd (v_1,v_2,v_3,v_4,d)=1$). We found 654077 such weight systems which satisfy $\overline{(C2)}$. Only 103 of them do not satisfy (C2). Up to $d=200$, there are 185,013 weight systems as above with $\overline{(C2)}$, and only 23 of them do not satisfy (C2). Table 1 lists these 23 weight systems $(v_1,v_2,v_3,v_4;d)$ in the lexicographic ordering with respect to $(d,v_1,v_2,v_3,v_4)$. It also gives the Milnor number $\mu$, the number L of the weight system in the lexicographic ordering with respect to $(d,v_1,v_2,v_3,v_4)$ of all weight systems as above which satisfy $\overline{(C2)}$, and a tuple $[a_1,a_2,a_3,a_4,a_5,a_6]\in \{0,1,2,3,4\}^6$ which says the following. Write

$$\begin{aligned} (J_1,J_2,J_3,J_4,J_5,J_6)=(\{1,2\},\{1,3\},\{1,4\}, \{2,3\},\{2,4\},\{3,4\}). \end{aligned}$$

Then, $a_i=|\{k\in N\,|\, ({\mathbb {N}}_0^{J_i})_{d-v_k}\ne \emptyset \}|$. That (C2) is not satisfied implies that for at least one $i\in \{1,2,3,4,5,6\}$ the number $a_i$ is $\le 1$.

Table 1 All reduced weight systems $(v_1,v_2,v_3,v_4;d)$ with $d\le 200$, $\frac{d}{2}>v_1\ge v_2\ge v_3\ge v_4$, and condition $\overline{(C2)}$, but not condition (C2)

The table does not contain Ivlev’s example (58, 33, 24, 1; 265) because $265>200$. Ivlev’s example has Milnor number 66516. All examples in Table 1 have smaller Milnor numbers. We checked also with PARI/GP for all 103 reduced weight systems with $d\le 360$ and $\overline{(C2)}$, but not (C2), that $\rho _{(\mathbf{v};d)}\in {\mathbb {N}}_0[t]$ holds. It is not clear whether there are weight systems with larger d which satisfy $\overline{(C2)}$ and $\rho _{(\mathbf{v};d)}\in {\mathbb {Z}}[t]-{\mathbb {N}}_0[t]$.

Arnold [2] associated with each reduced weight system $(v_1,\ldots ,v_n;d)$ which satisfies $\overline{(C2)}$ one type or several types in the following way. A type is a conjugacy class with respect to the symmetric group $S_n$ of a (not necessarily bijective) map $\sigma :N\rightarrow N$. Here, $\sigma$ is a map which satisfies $v_j|(d-v_{\sigma (j)})$ for $j\in N$. For each $j\in N$ such a $\sigma (j)$ exists because of condition $\overline{(C2)}$ for sets $J\subset N$ with $|J|=1$. The number of types is 3 for $n=2$, 7 for $n=3$ [2], 19 for $n=4$ [24], 47 for $n=5$ and 128 for $n=6$ [7, Examples 3.2]. In [24], the types for $n=4$ are numbered $I,II,\ldots ,XIX$. (This is reproduced in [7, Example 3.2 (iii)].) At most 9 of the 19 types allow weight systems which satisfy $\overline{(C2)}$, but not (C2), the weight systems V, VIII, XI, XII, XIII, XV, XVI, XVII and XIX. The other ten types allow only weight systems of Thom–Sebastiani sums of cycle-type singularities and chain-type singularities. The 23 weight systems in Table 1 realize seven of the nine types, and they do not realize XIII and XIX.

Remark 6.10

(i) K. Saito conjectured [20, (3.13) and (4.2)] that the weight system $\mathbf{w}=(w_1,\ldots ,w_n;1)$ of an isolated quasihomogeneous singularity with multiplicity $\ge 3$ satisfies $\psi _\mathbf{w}(d_\mathbf{w})>0$. Here, $d=d_\mathbf{w}$ for the equivalent reduced integer weight system $(v_1,\ldots ,v_n;d)$, because condition (C2) for the set $J=N$ implies $v_j|d$ for any j. Counter-examples with $n=4$ to this conjecture are given in [10, Examples 5.5]. The tables in [6] show that for $n=4$ and $\mu \le 500$, the only counter-examples are those in [10, Examples 5.5]. Problem 5 (b) asked for an answer to the question whether in the case $n=4$ and $\mu \ge 501$, the only counter-examples are those in [10, Examples 5.5]. We did not settle this.

(ii) With the software PARI/GP [23], we checked that for $n=5$ and $d\le 200$, only ten counter-examples to the conjecture in part (i) exist. They are all obvious generalizations of the examples in [10, Examples 5.5]. They are given in the following table. They are Thom–Sebastiani sums of singularities of type $A_k$, $D_k$ (with odd k), and/or a chain-type singularity with one of the three normalized weight systems

$$\begin{aligned} K_1:\ \Bigl (\frac{1}{4},\frac{3}{20},\frac{17}{40};1\Bigr ),\quad K_2:\ \Bigl (\frac{1}{4},\frac{3}{20},\frac{25}{56};1\Bigr ),\quad K_3:\ \Bigl (\frac{1}{6},\frac{5}{18},\frac{13}{36};1\Bigr ). \end{aligned}$$

(See [10, ch. 4 and 5] for formulas around the singularities $A_k$, $D_k$ and the chain-type singularities.) The number L has the same meaning as in Remark 6.9. We calculated with PARI/GP also the number of all reduced weight systems $(v_1,v_2,v_3,v_4,v_5;d)$ with $\overline{(C2)}$ and $d\le 200$ and $\frac{d}{2}>v_1\ge \cdots \ge v_5$. It is 1176435.

Table 2 All reduced weight systems $(v_1,v_2,v_3,v_4,v_5;d)$ with $d\le 200$, $\frac{d}{2}>v_1\ge \cdots \ge v_5$, condition $\overline{(C2)}$, and $\psi _\mathbf{w}(d_\mathbf{w})=0$

(iii) K. Saito posed also the weaker conjecture [20, (3.13) and (4.2)] that the weight system $\mathbf{w}$ of any isolated quasihomogeneous singularity satisfies $\psi _\mathbf{w}(d_\mathbf{w})>0$ or $\psi _\mathbf{w}(d_\mathbf{w}/2)>0$. Problem 5 (a) in [10] rephrases this conjecture. If the only counter-examples to the stronger conjecture in part (i) are the obvious generalizations of the examples 5.5 in [10], the weaker conjecture is true. But this is not clear.