Statistics on quasi-Stirling permutations of multisets

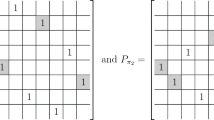
Abstract

A permutation $\pi$ of a multiset is said to be a quasi-Stirling permutation if there do not exist four indices $i<j<k<\ell$ such that $\pi _i=\pi _k$, $\pi _j=\pi _{\ell }$ and $\pi _i\ne \pi _j$. Define

$$\begin{aligned} \overline{Q}_{\mathcal {M}}(t,u,v)=\sum _{\pi \in \overline{\mathcal {Q}}_{\mathcal {M}}}t^{\mathrm{des}(\pi )}u^{\mathrm{asc}(\pi )}v^{\mathrm{plat}(\pi )}, \end{aligned}$$

where $\overline{\mathcal {Q}}_{\mathcal {M}}$ denotes the set of quasi-Stirling permutations of the multiset $\mathcal {M}$, and $\mathrm{asc}(\pi )$ (resp. $\mathrm{des}(\pi )$, $\mathrm{plat}(\pi )$) denotes the number of ascents (resp. descents, plateaux) of $\pi$. Denote by $\mathcal {M}^{\sigma }$ the multiset $\{1^{\sigma _1}, 2^{\sigma _2}, \ldots , n^{\sigma _n}\}$, where $\sigma =(\sigma _1, \sigma _2, \ldots , \sigma _n)$ is an n-composition of K for positive integers K and n. In this paper, we show that $\overline{Q}_{\mathcal {M}^{\sigma }}(t,u,v)=\overline{Q}_{\mathcal {M}^{\tau }}(t,u,v)$ for any two n-compositions $\sigma$ and $\tau$ of K. This is accomplished by establishing an $(\mathrm{asc}, \mathrm{des}, \mathrm{plat})$-preserving bijection between $\overline{\mathcal {Q}}_{\mathcal {M}^{\sigma }}$ and $\overline{\mathcal {Q}}_{\mathcal {M}^{\tau }}$. As applications, we obtain generalizations of several results for quasi-Stirling permutations on $\mathcal {M}=\{1^k,2^k, \ldots , n^k\}$ obtained by Elizalde and solve an open problem posed by Elizalde.