Abstract
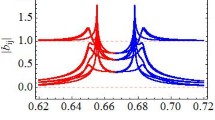
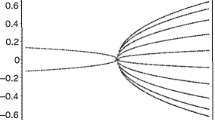
We propose an analysis technique for the exceptional points (EPs) occurring in the discrete spectrum of open quantum systems (OQS), using a semi-infinite chain coupled to an endpoint impurity as a prototype. We outline our method to locate the EPs in OQS, further obtaining an eigenvalue expansion in the vicinity of the EPs that gives rise to characteristic exponents. We also report the precise number of EPs occurring in an OQS with a continuum described by a quadratic dispersion curve. In particular, the number of EPs occurring in a bare discrete Hamiltonian of dimension n D is given by n D(n D−1); if this discrete Hamiltonian is then coupled to continuum (or continua) to form an OQS, the interaction with the continuum generally produces an enlarged discrete solution space that includes a greater number of EPs, specifically \(2^{n_{\mathrm{C}}} (n_{\mathrm{C}} + n_{\mathrm{D}} ) [ 2^{n_{\mathrm{C}}} (n_{\mathrm{C}} + n_{\mathrm{D}} ) - 1] \), in which n C is the number of (non-degenerate) continua to which the discrete sector is attached. Finally, we offer a heuristic quantum phase transition analogy for the emergence of the resonance (giving rise to irreversibility via exponential decay) in which the decay width plays the role of the order parameter; the associated critical exponent is then determined by the above eigenvalue expansion.



Similar content being viewed by others
Notes
For an example of a multi-channel model, consider the two-chain model in [16], in which it is straight-forward to derive the effective Hamiltonian H eff of dimension 3, giving rise to 12 solutions.
References
Heiss, W.D.: Phases of wave functions and level repulsion. Eur. Phys. J. D 7, 1 (1999)
Dembowski, C., Gräf, H.-D., Harney, H.L., Heine, A., Heiss, W.D., Rehfeld, H., Richter, A.: Experimental observation of the topological structure of exceptional points. Phys. Rev. Lett. 86, 787 (2001)
Dembowski, C., Dietz, B., Gräf, H.-D., Harney, H.L., Heine, A., Heiss, W.D., Richter, A.: Observation of a chiral state in a microwave cavity. Phys. Rev. Lett. 90, 034101 (2003)
Lee, S.-B., Yang, J., Moon, S., Lee, S.-Y., Shim, J.-B., Kim, S.W., Lee, J.-H., An, K.: Observation of an exceptional point in a chaotic optical microcavity. Phys. Rev. Lett. 103, 134101 (2009)
Rotter, I.: A non-Hermitian Hamilton operator and the physics of open quantum systems. J. Phys. A, Math. Theor. 42, 153001 (2009)
Rubinstein, J., Sternberg, P., Ma, Q.: Bifurcation diagram and pattern formation of phase slip centers in superconducting wires driven with electric currents. Phys. Rev. Lett. 99, 167003 (2007)
Moiseyev, N., Friedland, S.: Association of resonance states with the incomplete spectrum of finite complex-scaled Hamiltonian matrices. Phys. Rev. A 22, 618 (1980)
Lefebvre, R., Atabek, O., Šindelka, M., Moiseyev, N.: Resonance coalescence in molecular photodissociation. Phys. Rev. Lett. 103, 123003 (2009)
Cartarius, H., Main, J., Wunner, G.: Exceptional points in atomic spectra. Phys. Rev. Lett. 99, 173003 (2007)
Hernández, E., Jáuegui, A., Mondragón, A.: Non-Hermitian degeneracy of two unbound states. J. Phys. A, Math. Gen. 39, 10087 (2006)
Zirnbauer, M.R., Verbaarschot, J.J.M., Weidenmüller, H.A.: Destruction of order in nuclear spectra by a residual GOE interaction. Nucl. Phys. A 411, 161 (1983)
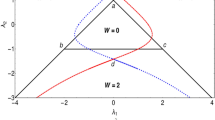
Cejnar, P., Heinze, S., Macek, M.: Coulomb analogy for non-Hermitian degeneracies near quantum phase transitions. Phys. Rev. Lett. 99, 100601 (2007)
Kato, T.: Perturbation Theory for Linear Operators, pp. 62–66. Springer, Berlin (1980)
Petrosky, T., Ting, C.-O., Garmon, S.: Strongly coupled matter field and nonanalytic decay rate of dipole molecules in a waveguide. Phys. Rev. Lett. 94, 043601 (2005)
Longhi, S.: Spectral singularities in a non-Hermitian Friedrichs-Fano-Anderson model. Phys. Rev. B 80, 165125 (2009)
Garmon, S., Nakamura, H., Hatano, N., Petrosky, T.: Two-channel quantum wire with an adatom impurity: role of the van Hove singularity in the quasibound state in continuum, decay rate amplification, and the Fano effect. Phys. Rev. B 80, 115318 (2009)
Bustos-Marún, R.A., Coronado, E.A., Pastawski, H.M.: Buffering plasmons in nanoparticle waveguides at the virtual-localized transition. Phys. Rev. B 82, 035434 (2010)
Bulgakov, E.N., Rotter, I., Sadreev, A.F.: Phase rigidity and avoided level crossings in the complex energy plane. Phys. Rev. E 74, 056204 (2006)
Jung, C., Müller, M., Rotter, I.: Phase transitions in open quantum systems. Phys. Rev. E 60, 114 (1999)
Longhi, S.: Nonexponential decay via tunneling in tight-binding lattices and the optical Zeno effect. Phys. Rev. Lett. 97, 110402 (2006)
Longhi, S.: Bound states in the continuum in a single-level Fano-Anderson model. Eur. Phys. J. B 57, 45 (2007)
Tanaka, S., Garmon, S., Ordonez, G., Petrosky, T.: Electron trapping in a one-dimensional semiconductor quantum wire with multiple impurities. Phys. Rev. B 76, 153308 (2007)
Hatano, N., Sasada, K., Nakamura, H., Petrosky, T.: Some properties of the resonant state in quantum mechanics and its computation. Prog. Theor. Phys. 119, 187 (2008)
Sasada, K., Hatano, N., Ordonez, G.: Resonant spectrum analysis of the conductance of an open quantum system and three types of Fano parameter. J. Phys. Soc. Jpn. 80, 104707 (2011)
Hatano, N.: Equivalence of the effective Hamiltonian approach and the Siegert boundary condition for resonant states. Fortschr. Phys. (2012). doi:10.1002/prop.201200064
Jarlebring, E., Kvaal, S., Michiels, W.: Computing all pairs (λ,μ) such that λ is a double eigenvalue of A+μB. KU Leuven, TW559 (2010)
Lefebvre, R., Moiseyev, N.: Localization of exceptional points with Padé approximants. J. Phys. B, At. Mol. Opt. Phys. 43, 095401 (2010)
Uzdin, R., Lefebvre, R.: Finding and pinpointing exceptional points of an open quantum system. J. Phys. B, At. Mol. Opt. Phys. 43, 235004 (2010)
Garmon, S., Petrosky, T., Nikulina, Y., Segal, D.: Amplification of non-Markovian decay due to bound state absorption into continuum. Fortschr. Physik (2012). arXiv:1204.6141
Fuchs, B.A., Levin, V.I.: Functions of a Complex Variable, vol. II. Pergamon Press, New York (1961)
Economou, E.N.: Green’s Functions in Quantum Physics, 2nd edn. Springer, Berlin (1983)
Chiu, C.B., Misra, B., Sudarshan, E.C.G.: The evolution of unstable states and a resolution of Zeno’s paradox. Phys. Rev. D 16, 520 (1977)
Fonda, L., Ghirardi, G.C., Rimini, A.: Decay theory of unstable quantum systems. Rep. Prog. Phys. 41, 587 (1978)
Martorell, J., Muga, J.G., Spring, D.W.L.: Quantum Post-Exponential Decay. In: Lect. Notes Phys., vol. 789, p. 239. Springer, Berlin (2009)
Dente, A.D., Bustos-Marún, R.A., Pastawski, H.M.: Dynamical regimes of a quantum SWAP gate beyond the Fermi golden rule. Phys. Rev. A 78, 062116 (2008)
Mostafazadeh, A.: Spectral singularities of complex scattering potentials and infinite reflection and transmission coefficients at real energies. Phys. Rev. Lett. 102, 220402 (2009)
Knopp, K.: Theory of Functions, Pt. 2, pp. 126–129. Dover, New York
Sachdev, S.: Quantum Phase Transitions. Cambridge University Press, Cambridge (2001)
Schindler, J., Li, A., Zheng, M.C., Ellis, F.M., Kottos, T.: Experimental study of active LRC circuits with \(\mathcal {PT}\)-symmetries. Phys. Rev. A 84, 040101(R) (2011)
Bender, C.M., Boettcher, S.: Real spectra in non-Hermitian Hamiltonians having \(\mathcal {PT}\)-symmetry. Phys. Rev. Lett. 80, 5243 (1998)
Acknowledgements
We would like to thank E.C.G. Sudarshan, G. Ordonez, J. Pixley and S. Kirchner for stimulating discussion on the QPT analogy and T. Petrosky for helpful comments on an earlier draft. The research of S.G. was supported by CQIQC, the Sloan research fellowship of D.S. and MPI-PKS. The research of N.H. was supported by Grant-in-Aid for Scientific Research No. 17340115 from the Ministry of Education, Culture, Sports, Science and Technology of Japan.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Derivation of the Effective Hamiltonian H eff for the Prototype Model
In order to keep our presentation reasonably self-contained, we briefly outline the method from Ref. [25] to obtain the effective Hamiltonian reported in Eq. (13) from the full Hamiltonian for our prototype model given in Eq. (8). We start by writing the wavefunction along the chain in generic form as
with C an undetermined normalization constant. To solve the model from this point we find it useful to close the Schrödinger equation on the right with an arbitrary bra 〈x| to obtain
in which H is the full Hamiltonian from Eq. (8), while x might represent the impurity site or any site along the chain x∈{d,1,2,…}. If we specify any site x>2 and plug Eq. (8) into Eq. (27) then, after applying the usual commutation relations, we find
Then plugging in Eq. (26) for the wave function we immediately find ϵ k =−cosk for the dispersion along the chain. Next we solve for the normalization constant C by choosing x=2 in Eq. (27), which yields
After applying ϵ k =−cosk here we re-arrange to find C=〈1|ψ〉e −ik.
Finally, evaluating Eq. (27) for the cases x=1 and x=d we obtain the matrix equation
in which ϵ=z is the discrete eigenvalue associated with the impurity sector. Applying the transformation k=cos−1(−z) in the 2×2 matrix on the LHS of this equation we find \(- e^{i k} = z - \sqrt{z^{2} - 1} = \varSigma(z)\), hence we obtain the effective Hamiltonian H eff reported in Eq. (13) in the main text. We now obtain the characteristic equation by solving det(z−H eff(z))=0, as reported in Eq. (10).
Appendix B: Comment on the Number of Discrete Solutions Resulting from a General Effective Hamiltonian H eff
In this Appendix we briefly comment on the number of solutions emerging from the characteristic equation under the effective Hamiltonian treatment (the reader should also consult Appendices D and H of [24] for similar discussions). Let us consider a slightly more general form for H eff of dimension two as
(compare this with H eff from Eq. (30) for the semi-infinite chain model with an endpoint impurity). Note that we may just as well solve the characteristic equation in terms of k rather than z by writing det(z(k)−H eff(k))=0, which gives
after applying the transformation z(k)=−cosk=(e ik+e −ik)/2 for a tight-binding chain. Making the replacement w=e ik here and multiplying through by w 2 immediately yields a fourth order polynomial equation for w, hence a general effective Hamiltonian of dimension two should be expected to yield four discrete eigenvalues. From this point it is not difficult to convince oneself that adding a single discrete impurity site increases the dimension of H eff by one and simultaneously introduces two new solutions to the characteristic equation (it is in this sense we say that ϵ k =−cosk represents a quadratic dispersion in the leads). Meanwhile, adding a new channel also increases the dimension of H eff by one but also requires us to solve a second polynomial equation, hence doubling the total number of solutions after the increase in the dimension of the effective Hamiltonian has already been taken into account.
However, our semi-infinite chain model with an endpoint impurity happens to have the special value F=1/2, which we note is the only value for F under which the order of the polynomial Eq. (32) is reduced from four to two. Hence our present model represents a special case with regard to the number of discrete solutions (and therefore the number of EPs as well).
Rights and permissions
About this article
Cite this article
Garmon, S., Rotter, I., Hatano, N. et al. Analysis Technique for Exceptional Points in Open Quantum Systems and QPT Analogy for the Appearance of Irreversibility. Int J Theor Phys 51, 3536–3550 (2012). https://doi.org/10.1007/s10773-012-1240-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-012-1240-5