Predicting rapid progression phases in glaucoma using a soft voting ensemble classifier exploiting Kalman filtering

Abstract

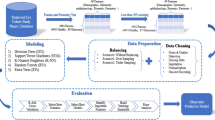
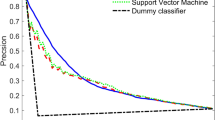
In managing patients with chronic diseases, such as open angle glaucoma (OAG), the case treated in this paper, medical tests capture the disease phase (e.g. regression, stability, progression, etc.) the patient is currently in. When medical tests have low residual variability (e.g. empirical difference between the patient’s true and recorded value is small) they can effectively, without the use of sophisticated methods, identify the patient’s current disease phase; however, when medical tests have moderate to high residual variability this may not be the case. This paper presents a framework for handling the latter case. The framework presented integrates the outputs of interacting multiple model Kalman filtering with supervised learning classification. The purpose of this integration is to estimate the true values of patients’ disease metrics by allowing for rapid and non-rapid phases; and dynamically adapting to changes in these values over time. We apply our framework to classifying whether a patient with OAG will experience rapid progression over the next two or three years from the time of classification. The performance (AUC) of our model increased by approximately 7% (increased from 0.752 to 0.819) when the Kalman filtering results were incorporated as additional features in the supervised learning model. These results suggest the combination of filters and statistical learning methods in clinical health has significant benefits. Although this paper applies our methodology to OAG, the methodology developed is applicable to other chronic conditions.

Appendices

Appendix A: Detailed description of case study model inputs

Featured measured	Feature engineering	Description	Data used
	function
Progression	Expanding window	Using an expanding window measure progression	MD, KF MD
		from periods 3 to T, engineer the features OLSR
		slope, OLSR slope p-value, and a binary indicator
		indicating if the slope is statistically significant at
		the level of 0.05
		Calculate summary statistics of mean, standard
		deviation, quantiles at various levels, min, and
		max for each covariate described in the above row.
	Moving window	Calculate a moving window of 3 most recent
		periods from periods 3 to T for OLSR slope, and
		OLSR p-value.
Patient Test	Expanding window	Using an expanding window calculate summary	MD, PSD, IOP,
Results		statistics mean, standard deviation, various	KF MD
		quantiles, min, and max from periods 0 to T.
	Moving window	Using a moving window of 3 & 4 periods,
		calculate summary statistics (e.g., mean, standard
		deviation, quantiles, min, and max).
	Shifted/ Time-lag	Time lag features in addition to time T: T-3,
	features	T-2, T-1.
Demographics	N/A	Unchanging covariates based on patient’s
		demographic information.
	Age, Sex, Race
Patient Appointment	N/A	Follow-up period.	Visit Period (6-month
Information			interval)

Appendix B: IMM initial filter model parameters

The bank of Kalman Filters was iteratively tuned using a grid search procedure. The objective of this procedure was to determine the best parameters for the Kalman filter models. The initial estimates for M and μ₀ were obtained using the data. M was estimated using the number of transitions between RP and RP; RP and Non-RP; Non-RP and RP; and Non-RP and Non-RP. μ₀ was estimated using the normalized frequency of RP instances and Non-RP instances. The estimated values for M and μ₀ are found in Tables 8 and 9 respectively.

Table 8 IMM initial transition probability matrix, M

Table 9 IMM Initial mode probability matrix, μ

The elements of the F matrix are shown in Table 10. The F matrix captures the system transition of Kalman Filter. The F matrix was built using the linear vector difference equation model for the following physics equations:

$$ \begin{array}{@{}rcl@{}} MD_{predicted} &=& MD + (MD_{velocity}\cdot{\Delta} t)\\ &+& \left( MD_{acceleration}\cdot \frac{{{\Delta} t}^{2}}{2}\right) \end{array} $$

(19)

$$ MD_{predicted velocity} = MD_{velocity} + MD_{acceleration} \cdot {\Delta} t $$

(20)

$$ \begin{array}{@{}rcl@{}} MD_{predicted acceleration} = MD_{acceleration}, \end{array} $$

(21)

where Δt = 6 months, and state variables x = 〈MD MD_velocity MD_acceleration〉.

Table 10 Transition matrix, F

The Q (process) noise covariance matrices are shown in Tables 11 and 12. The Q matrix captures the noise introduced into our system due to external factors we do not directly model for. The Q matrix captures this noise using a random process centered at 0. In our model we assumed the Q matrices have a piecewise white noise model, where the noise follows a discrete time Wiener process. This noise model assumes the noise for the highest order term (e.g. acceleration) is constant for the duration of each time period, but differs for each time period, and each of these is uncorrelated between time periods [21].

Table 11 Non-RP process noise covariance matrix, Q₁

Table 12 RP process noise covariance matrix, Q₂

The initial estimates for the MD, MD velocity, and MD acceleration variances are high, so as to model the uncertainty associated with these three measurements when you see a new patient (Table 13).

Table 13 Initial covariance matrix, P

As a clinician with a new patient there is no current information to suggest an appropriate MD rate of change. There is only a single MD baseline value. As such the initial state estimate for each patient is

$$ x = \begin{pmatrix} MD_{baseline} \\ 0\\ 0 \end{pmatrix} $$

(22)

Last, the measurement function, H, and measurement noise, R are defined respectively as,

$$ H = \begin{pmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} $$

(23)

$$ R = \begin{pmatrix} \sigma_{1} & 0 & 0 \\ 0 & \sigma^{2} & 0 \\ 0 & 0 & \sigma_{3} \end{pmatrix}. $$

(24)

Appendix C: Illustration of the IMM Kalman filtered MD results compared to the patient’s MD results and the MD “true state” estimated by OLSR

Fig. 4

Illustration of the IMM Kalman filtered MD results compared to the patient’s MD results and the MD “true state” estimated by OLSR