Designing schedule configuration of a hybrid appointment system for a two-stage outpatient clinic with multiple servers

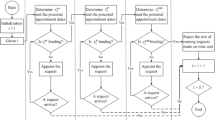
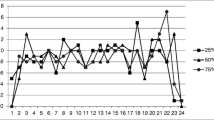
Abstract

Even though several clinics serve patients in more than one stage (e.g., visit nurse and then visit doctor) and employ multiple providers in each stage, most of the previous work on appointment system design considers a simplified single-stage single-server clinic. Motivated by a real-life clinic setting, this paper aims to determine the schedule configuration of a hybrid appointment system (i.e., the number of pre-booking and same-day time slots reserved for a physician along with their positions in the schedule) for a two-stage multi-server clinic. A stochastic optimization model is developed to obtain a schedule configuration that minimizes the expected total cost - a weighted sum of excessive patient waiting time, resource idle time, resource overtime, and denied appointment requests. Owing to its computational complexity, we estimate the expected total cost using the sample average approximation method. The proposed model is verified and validated using small test instances and subject matter experts. A case study of a family medicine clinic in Pennsylvania is used to illustrate the proposed approach. The schedule generated by the proposed model results in a significantly lower expected cost compared to the approximated single-stage system’s best schedule configuration and clinic’s existing configuration. Further, sensitivity analysis is conducted to assess the impacts of no-show rate, service time variation, and cost ratios on the schedule configuration. Our findings demonstrate that the schedule configuration is sensitive to changes in the average no-show rate and cost ratios but is not significantly impacted by service time variation. Several managerial insights are also drawn from our analysis. Finally, we provide directions for future research that also highlights the potential to use the revenue management approach to address the problem under study.

Appendices

Appendix A: linearization techniques

In this section, three different linearization techniques are proposed to transform the non-linear constraints to equivalent linear constraints. These linearization techniques are used to avoid non-linearity and formulate stochastic MILP model for designing the hybrid appointment system.

1.1 A.1 Linearization technique - 1

To illustrate Linearization Technique - 1, let us consider the non-negative continuous decision variables, y and x_j, where j = 1, 2..., n. In addition, let us consider the following binary decision variables, ${{\Delta }_{i}^{j}}$ where j = 1, 2,..., n and i = 1, 2,..., I_j. If the optimization model seeks to minimizey and if y is equal to the maximum of n non-linear terms, where each non-linear term is the product of one continuous variable and one or more binary decision variables as shown in constraint (37), then the non-linear constraint can be linearized by introducing a binary variable 𝜃^j for each x_j as shown in Eqs. 38–44

$$ \begin{array}{@{}rcl@{}} \text{Non-Linear Constraint:} \displaystyle y = \max\Big(x_{1} \times \prod\limits_{i=1}^{I_{1}} {{\Delta}_{i}^{1}}, x_{2} \times \prod\limits_{i=1}^{I_{2}} {{\Delta}_{i}^{2}}, ..., x_{n} \times \prod\limits_{i=1}^{I_{n}} {{\Delta}_{i}^{n}} \Big) \end{array} $$

(37)

$$ \begin{array}{@{}rcl@{}} \text{Equivalent Linear Constraints:}&& \displaystyle y \geq x_{1} - M (I_{1} - \sum\limits_{i=1}^{I_{1}} {{\Delta}_{i}^{1}}) \end{array} $$

(38)

$$ \begin{array}{@{}rcl@{}} &&\displaystyle y \geq x_{2} - M (I_{2} - \sum\limits_{i=1}^{I_{2}} {{\Delta}_{i}^{2}}) \end{array} $$

(39)

$$ \begin{array}{@{}rcl@{}} && \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ & & \displaystyle y \geq x_{n} - M (I_{n} - \sum\limits_{i=1}^{I_{n}} {{\Delta}_{i}^{n}}) \end{array} $$

(40)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq x_{1} + M (1 - \theta^{1}) \end{array} $$

(41)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq x_{2} + M (1 - \theta^{2}) \end{array} $$

(42)

$$ \begin{array}{@{}rcl@{}} & & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ & & \displaystyle y \leq x_{n} + M (1 - \theta^{n}) \end{array} $$

(43)

$$ \begin{array}{@{}rcl@{}} & & \displaystyle \sum\limits_{j=1}^{n} \theta^{j} = 1 \end{array} $$

(44)

Constraints (38)–(40) becomes active if all the binary variable associated with that constraint is 1 and becomes inactive even if one of the binary variable is 0. For example, if all the ${{\Delta }_{i}^{1}}$’s are 1, then Constraint (38) becomes y ≥ x₁. Even if one of the ${{\Delta }_{i}^{1}}$’s is equal to 0 then Constraint (38) becomes y ≥ x₁ − M. Since M is a large positive number, the constraint is equivalent to y ≥−M and hence inactive. Constraint (44), forces exactly one of the 𝜃^j, j = 1, 2,..., n to be active, which in turn forces one of the Constraints (41)–(43) to be active. To ensure feasibility, the 𝜃^j, j = 1, 2,..., n corresponding to the maximum value of x_jj = 1, 2..., n becomes 1, and ensures that y takes the maximum value of x_j. This technique is used to linearize Eqs. (8), (11), (14), and (15).

1.2 A.2 Linearization technique - 2

To illustrate Linearization Technique - 2, let us consider two non-negative continuous decision variables, x and y and I binary decision variables, Δ_i, where i = 1, 2,..., I. If y is exactly equal to a non-linear term that is characterized by the product of x and Δ_i, where i = 1, 2,..., I as shown in Eq. 45, then it can be linearized using Eqs. 46–48. The condition represented by this constraint is that the variable y = x, if all the Δ_i’s are equal to one and y = 0 even if one of the Δ_i is zero.

$$ \begin{array}{@{}rcl@{}} && \text{Non-Linear Constraint:} \displaystyle y = x \times \prod\limits_{i=1}^{I} {\Delta}_{i} \end{array} $$

(45)

$$ \begin{array}{@{}rcl@{}} && \text{Equivalent Linear Constraints:} \displaystyle y \geq x - M (I- \sum\limits_{i=1}^{I} {\Delta}_{i}) \end{array} $$

(46)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq x + M (I- \sum\limits_{i=1}^{I} {\Delta}_{i}) \end{array} $$

(47)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq M ({\Delta}_{i} )\qquad\qquad\forall i \end{array} $$

(48)

If all the Δ_i’s are equal to one, then Constraints (46) and (47) will force y to be exactly equal to x and Constraint (48) becomes inactive. However, even if one of the Δ_i’s is equal to 1, then Constraints (46) and (47) will become inactive and Constraint (48) will force y to be equal to 0. This technique is used to linearize Constraints (10), (72)–(74).

In Eq. 45, if we have greater than or equal to (i.e., i.e., $y \geq x \times \prod \limits _{i=1}^{I} {\Delta }_{i}$) instead of strict equality, then the non-linear constraint can be linearized just by using Constraint (46).

1.3 A.3 Linearization technique - 3

To illustrate Linearization Technique - 3, let us consider non-negative continuous decision variables, y and x_i, where i = 1, 2..., I. If the objective function seeks to maximizey and if y is the maximum of x_i, as shown in Eq. 49, then it can be linearized using Eqs. 49–52. To linearize, we introduce a binary variable, δ_i, where i = 1, 2,..., I.

$$ \begin{array}{@{}rcl@{}} && \text{Non-Linear Constraint:} \displaystyle y = \max (x_{i} : i = 1,2,...,I) \end{array} $$

(49)

$$ \begin{array}{@{}rcl@{}} && \text{Equivalent Linear Constraints:} \displaystyle y \geq x_{i}\qquad\qquad\qquad\forall i \end{array} $$

(50)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq x_{i} + M(1-\delta_{i}) \qquad \qquad\forall i \end{array} $$

(51)

$$ \begin{array}{@{}rcl@{}} & & \displaystyle \sum\limits_{i=1}^{I} \delta_{i} = 1 \end{array} $$

(52)

Constraint (50) ensures that y is greater than or equal to the all the x_i’s. In other words, y must be greater than or equal to maximum of x_i, where i = 1, 2,..., I. Further, Constraint (51) is active (i.e., y ≤ x_i) only when the binary variable, δ_i, is 1 and Constraint (52) forces exactly one of the binary variables (δ_i’s) to take a value 1. Therefore, to ensure feasibility of Constraints (50) and (52), Constraint (51) will be active only for the maximum of x_i. Thus, Constraints (50) and (51) will force y to be exactly equal to the maximum of x_i’s. In this research, we use this procedure to linearize Constraints (18) and (19)

Appendix B: Linearization of the stochastic model

In this section, we present the equivalent linear equations for the non-linear constraints in the stochastic MILP model discussed in Section 5. To linearize Constraints (18) and (19), we introduce two binary variables, namely, δ_sn and Δ_sd. The variable δ_sn takes the value 1 if $L_{s-1,n}^{N}(\omega ) > b_{sn}^{N}$ and is 0 otherwise. Similarly, Δ_sd is 1 if $L_{s-1,d}^{D}(\omega ) > b_{sd}^{D}$ and 0 otherwise. In addition, we also introduce the binary variables $\theta ^{1}_{ptsn}(\omega )$, $\theta ^{2}_{ptsn}(\omega )$, $\theta ^{3}_{ptsn}(\omega )$, $\theta ^{4}_{ptsn}(\omega )$, ${\Theta }^{1}_{ptsd}(\omega )$, ${\Theta }^{2}_{ptsd}(\omega )$, ${\Theta }^{3}_{ptsd}(\omega )$, ${\Theta }^{4}_{ptsd}(\omega )$, α_ptsn(ω), and β_ptsd(ω) to determine the exact maximum for start time and latest completion times of the resources.

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \geq C_{p't^{\prime},s-1,n}^{N}(\omega) - M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t,t^{\prime} \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s\in \mathcal{S} \ni s>1, n \in \mathcal{N} \end{array} $$

(53)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \geq C_{p'tsn}^{N}(\omega) - M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad \forall t \in \mathcal{T}, p, p^{\prime} \in \mathcal{P}_{t}(\omega), p^{\prime} = 1,2,..,p-1, s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(54)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \geq b_{sn}^{N} - M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(55)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \leq C_{p't^{\prime},s-1,n}^{N}(\omega) + M\big(1 - \theta^{1}_{ptsn}(\omega)\big)\qquad\qquad\qquad\forall t,t^{\prime} \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s\in \mathcal{S} \ni s>1, n \in \mathcal{N} \end{array} $$

(56)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \leq C_{p'tsn}^{N}(\omega) + M\big(1 - \theta^{2}_{ptsn}(\omega)\big)\qquad\qquad \forall t \in \mathcal{T}, p, p^{\prime} \in \mathcal{P}_{t}(\omega), p^{\prime} = 1,2,..,p-1, s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(57)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \leq b_{sn}^{N} + M\big(1 - \theta^{3}_{ptsn}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(58)

$$ \begin{array}{@{}rcl@{}} \displaystyle \theta^{1}_{ptsd}(\omega)+\theta^{2}_{ptsd}(\omega)+\theta^{3}_{ptsd}(\omega)+\theta^{4}_{ptsn}(\omega) = \sum\limits_{n \in \mathcal{D}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(59)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsn}^{N}(\omega) \leq S_{ptsn}^{N}(\omega) + \eta_{pt}(\omega) \times (1 - \sigma_{pt}(\omega)) + M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big) \qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(60)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsn}^{N}(\omega) \geq S_{ptsn}^{N}(\omega) + \eta_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) - M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big) \qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(61)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsn}^{N}(\omega) \leq M\sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(62)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \geq C_{p't^{\prime},s-1,d}^{D}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t,t^{\prime}\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s \in \mathcal{S} \ni s > 1, d \in \mathcal{D} \end{array} $$

(63)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \geq C_{p'tsd}^{D}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} = 1,2,..,p-1, s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(64)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \geq \sum\limits_{n \in \mathcal{N}}^{} C_{ptsn}^{N}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(65)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \geq PAT_{sd}^{B} - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(66)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq C_{p't^{\prime},s-1,d}^{D}(\omega) + M\big(1 - {\Theta}^{1}_{ptsd}(\omega)\big)\qquad\qquad\qquad\forall t,t^{\prime}\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s \in \mathcal{S} \ni s > 1, d \in \mathcal{D} \end{array} $$

(67)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq C_{p'tsd}^{D}(\omega) + M\big(1 - {\Theta}^{2}_{ptsd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} = 1,2,..,p-1, s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(68)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq \sum\limits_{n \in \mathcal{N}}^{} C_{ptsn}^{N}(\omega) + M\big(1 - {\Theta}^{3}_{ptsd}(\omega)\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(69)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq PAT_{sd}^{B} + M\big(1 - {\Theta}^{4}_{ptsd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(70)

$$ \begin{array}{@{}rcl@{}} \displaystyle {\Theta}^{1}_{ptsd}(\omega)+{\Theta}^{2}_{ptsd}(\omega)+{\Theta}^{3}_{ptsd}(\omega)+{\Theta}^{4}_{ptsd}(\omega) = \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(71)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsd}^{D}(\omega) \leq S_{ptsd}^{D}(\omega) + \rho_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) + M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big) \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(72)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsd}^{D}(\omega) \geq S_{ptsd}^{D}(\omega) + \rho_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{}X_{ptsnd}(\omega)\big) \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(73)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsd}^{D}(\omega) \leq M\sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(74)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sn}^{N}(\omega) \geq C_{ptsn}^{N}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(75)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sn}^{N}(\omega) \leq C_{ptsn}^{N}(\omega) + M\big(1 - \alpha_{ptsn}\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(76)

$$ \begin{array}{@{}rcl@{}} \displaystyle \sum\limits_{p\in\mathcal{P}_{t}(\omega)}\alpha_{ptsn} = 1\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N}\end{array} $$

(77)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sd}^{D}(\omega) \geq C_{ptsd}^{D}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(78)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sd}^{D}(\omega) \leq C_{ptsd}^{D}(\omega) + M\big(1 - \beta_{ptsn}\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(79)

$$ \begin{array}{@{}rcl@{}} \displaystyle \sum\limits_{p\in\mathcal{P}}\beta_{ptsn} = 1\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(80)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{s-1,n}^{N}(\omega) \leq b_{sn}^{N} + M(1- \delta_{sn}) \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, n \in \mathcal{N} \end{array} $$

(81)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{s-1,n}^{N}(\omega) \geq b_{sn}^{N} - M\delta_{sn} \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, n \in \mathcal{N} \end{array} $$

(82)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sn}^{N}(\omega) \leq b_{sn}^{N} + M(1-\delta_{sn}) \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, n \in \mathcal{N} \end{array} $$

(83)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sn}^{N}(\omega) \leq L_{s-1,n}^{N}(\omega) + M\delta_{sn}\qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, n \in \mathcal{N} \end{array} $$

(84)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{s-1,d}^{D}(\omega)\leq b_{sd}^{D} + M(1- {\Delta}_{sd}) \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, d \in \mathcal{D} \end{array} $$

(85)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{s-1,d}^{D}(\omega) \geq b_{sd}^{D} - M{\Delta}_{sd} \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, d \in \mathcal{D} \end{array} $$

(86)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) \leq b_{sd}^{D} + M(1-{\Delta}_{sd}) \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, d \in \mathcal{D} \end{array} $$

(87)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) \leq L_{s-1,d}^{D}(\omega) + M{\Delta}_{sd} \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, d \in \mathcal{D} \end{array} $$

(88)

Appendix C: Stochastic programming model for a single stage system

In this section, we present the stochastic program model to determine the best schedule configuration of an outpatient clinic with only one stage (doctor). The mathematical model presented in Section 5 can be easily adapted for a single-stage system by eliminating the variables and constraints involving the nurse stage. Therefore, to ensure consistency, we will use the notations presented in Section 5 but without the indices and sets representing the nurse stage. Thus, for the single stage system, the key decision variable is X_ptsd(ω) instead of X_ptsnd(ω). The objective function (89) is subject to Constraints (90)–(107).

$$ \begin{array}{@{}rcl@{}} &&\text{Minimize}, Z = \displaystyle\sum\limits_{\omega \in {\Omega}} \Bigg(p(\omega) \times \displaystyle{ c^{WT} \Big[ \sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega) }W_{pt}(\omega) \Big] + c^{DIT} \Big [ \sum\limits_{s \in \mathcal{S}} \sum\limits_{d \in \mathcal{D}} \Big(I_{sd}^{DB}(\omega) + I_{sd}^{DA}(\omega)\Big) \Big ] +} \\&&{ c^{DOT} \Big [ \sum\limits_{s \in \mathcal{S}} \sum\limits_{d \in \mathcal{D}} O_{sd}^{D}(\omega) \Big ]+ c^{OC} \Big[\sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega)}\Big(1- \sum\limits_{s \in \mathcal{S}}^{}\sum\limits_{d \in \mathcal{D}}^{}X_{ptsd}(\omega)\Big) \Big]} \Bigg ) \end{array} $$

(89)

$$ \begin{array}{@{}rcl@{}} \displaystyle\sum\limits_{d \in \mathcal{D}}^{}\sum\limits_{s \in \mathcal{S}}^{}X_{ptsd}(\omega) \leq 1\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), \omega \in {\Omega} \end{array} $$

(90)

$$ \begin{array}{@{}rcl@{}} \displaystyle X_{ptsd}(\omega) + X_{p't'sd}(\omega) \leq 1\qquad\qquad\qquad\forall t = {A}, t^{\prime} = {O}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(91)

$$ \begin{array}{@{}rcl@{}} \displaystyle \sum\limits_{t \in {T}} \sum\limits_{p \in \mathcal{P}_{t}(\omega) } X_{ptsd}(\omega) \leq \tau\qquad\qquad \forall d \in \mathcal{D}, s \in {S}, \omega \in {\Omega} \end{array} $$

(92)

$$ \begin{array}{@{}rcl@{}} \displaystyle R_{s}(\omega) = \sum\limits_{d \in \mathcal{D}}^{}\sum\limits_{p \in \mathcal{P}_{t}(\omega)}^{}X_{ptsd}(\omega) \qquad\qquad\forall t = \{A\}, s \in \mathcal{S}, \omega \in {\Omega} \end{array} $$

(93)

$$ \begin{array}{@{}rcl@{}} \displaystyle &&S_{ptsd}^{D}(\omega) = \max \Bigg\{ \Big(\sum\limits_{s \in \mathcal{S}}b_{sd}^{D} \times \sum\limits_{s \in \mathcal{S}}\sum\limits_{n \in \mathcal{N}} X_{ptsd}(\omega)\Big), \\ \ &&\Big(L_{s-1,d}^{D}(\omega) \times \sum\limits_{n \in \mathcal{N}} X_{ptsd}(\omega) : s\in \mathcal{S} \ni s>1 \Big), \\ &&\Big(C_{p'tsd}^{D}(\omega) \times X_{ptsd}(\omega): p^{\prime} \in \mathcal{P}_{t}(\omega) \ni p^{\prime} \leq p-1, s \in \mathcal{S}\Big) \Bigg\} \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(94)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq M X_{ptsd}(\omega)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(95)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsd}^{D}(\omega) = \Big(S_{ptsd}^{D}(\omega) + \rho_{pt}(\omega) \times (1 - \sigma_{pt}(\omega))\Big) \times X_{ptsd}(\omega) \qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(96)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sd}^{D}(\omega) = \max \Big(C_{ptsd}^{D}(\omega) \times X_{ptsd}(\omega) : t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega)\Big) \qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(97)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) = b_{sd}^{D} \qquad\qquad\qquad\forall s \in \mathcal{S} \ni s = 1, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(98)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) = \max \Big(b_{sd}^{D}, L_{s-1,d}^{D}(\omega)\Big)\qquad\qquad\qquad\forall s \in \mathcal{S} \ni s > 1, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(99)

$$ \begin{array}{@{}rcl@{}} \displaystyle I_{sd}^{DB}(\omega) \geq L_{sd}^{D}(\omega) - E_{sd}^{D}(\omega) - \sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega)}\rho_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) \times X_{ptsd}(\omega)\qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(100)

$$ \begin{array}{@{}rcl@{}} \displaystyle I_{sd}^{DA}(\omega) - O_{sd}^{D}(\omega) \geq f_{sd}^{D} - L_{sd}^{D}(\omega)\qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(101)

$$ \begin{array}{@{}rcl@{}} \displaystyle {O_{d}^{D}}(\omega) = L_{sd}^{D}(\omega) - f_{sd}^{D}\qquad\qquad\qquad\forall s \in \mathcal{S}\ni s = |\mathcal{S}|, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(102)

$$ \begin{array}{@{}rcl@{}} \displaystyle W_{pt}(\omega) = (1-\sigma_{pt}(\omega))\times\Bigg(\sum\limits_{s \in \mathcal{S}}^{}\sum\limits_{d \in \mathcal{D}}^{}\Big(S_{ptsd}^{D}(\omega) - b_{sd}^{D} \times X_{ptsd}(\omega)\Big)\Bigg) \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), \omega \in {\Omega} \end{array} $$

(103)

$$ \begin{array}{@{}rcl@{}} \displaystyle \hat{W}_{pt}(\omega) \geq W_{pt}(\omega) - \kappa\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), \omega \in {\Omega} \end{array} $$

(104)

$$ \begin{array}{@{}rcl@{}} \displaystyle R_{s}(\omega) - R_{s} = 0\qquad\qquad\qquad\forall s \in \mathcal{S}, \omega \in {\Omega} \end{array} $$

(105)

$$ \begin{array}{@{}rcl@{}} &&S_{ptsd}^{D}(\omega),C_{ptsd}^{D}(\omega), L_{sd}^{D}(\omega),DIT_{sd}^{\omega}, \\ &&I_{sd}^{DB}(\omega) , I_{sd}^{DA}(\omega), O_{sd}^{D}(\omega),W_{pt}^{}(\omega) \geq 0\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(106)

$$ \begin{array}{@{}rcl@{}} &&X_{ptsd}(\omega) \in \{0, 1\}\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(107)