Abstract
In this paper, the dynamic correlation of Japanese stock returns is estimated by using the dynamic conditional correlation (DCC–GARCH) model to study their correlation dynamics empirically. It is difficult to fit the model to the whole stock market jointly at the same time; therefore, a network-based clustering is applied for the dimensionality reduction of the sample data. Two types correlation structures are estimated: homogeneous groups of stocks in a balanced size are created by clustering to observe within-group correlation, while a single portfolio that comprises group portfolio returns is also created to observe between-group correlation. The estimation result reveals dynamic changes in correlation intensity represented by the largest eigenvalue of the estimated correlation matrix. A higher level of correlation intensity and volatility are observed during the crisis periods, namely after both the Lehman collapse and the Great East Japan Earthquake, for the between- and within-group correlations. It is also confirmed that the pattern of correlation change is significantly different between the groups. The proposed method is useful for monitoring dynamic correlation of asset returns efficiently in a large scale of portfolio.






Similar content being viewed by others
Notes
The degrees \(\left( {p_{1}},\ {q_{1}}\right) \) can take different values for every stock return, while the values and diagonal elements of \(\varvec{A}_{i}\) and \(\varvec{B}_{i}\) are determined empirically.
The degrees \(\left( p_{2},\ q_{2}\right) \) can take different values for every stock return, while the values and diagonal elements of \(\varvec{S}_{i}\) and \(\varvec{T}_{i}\) are determined empirically.
\(\frac{1}{\sqrt{h_{i{\cdot }t}}}\) in Eq. (12) is the Jacobian of the variable transformation between \(r_{t}\) and \(z_{t}\).
We use the skew t-distribution defined by Fernández and Steel (1998). The density function of the skew t distribution \(f\left( x|\xi ,\eta \right) \) is defined as
$$\begin{aligned} {\left\{ \begin{array}{ll} f\left( x|\xi ,\eta \right) =\frac{2}{\xi +\frac{1}{\xi }}\,f\left( \xi x|\eta \right) &{} for\;\;x<0\\ f\left( x|\xi ,\eta \right) =\frac{2}{\xi +\frac{1}{\xi }}\,f\left( \frac{x}{\xi }|\eta \right) &{} for\;\;x\ge 0 \end{array}\right. } \end{aligned}$$(13)where \(\xi \in \left( 0,\,\infty \right) \) is a skewness parameter; \(f\left( x|\eta \right) \) is the desity function of the Student t distribution with the degree of freedom \(\eta \in \left( 0,\,\infty \right) \).
The Student t-copula is defined as
$$\begin{aligned} C^{S_t}\left( \varvec{u}|\eta ,\varvec{R}\right) =\varvec{t}_{\eta {\cdot }\varvec{R}}\left( t_{\eta }^{-1}\left( u_{1}\right) ,\ldots ,\ t_{\eta }^{-1}\left( u_{N}\right) \right) \end{aligned}$$(14)where \(\varvec{R}\) is a correlation matrix, \(\eta \in \left( 0,\,\infty \right) \) is the degree of freedom, \(t_{\eta }\left( \ \right) \) is the cdf of the univariate Student t-distribution, and \(\varvec{t}_{\eta {\cdot }\varvec{R}}\) is the cdf of the multivariate Student t-distribution. The density function of the Student t-copula is defined as
$$\begin{aligned} c^{S_t}\left( \varvec{u}|\eta ,\varvec{R}\right) =\frac{\mathrm {\Gamma }\left( \frac{\eta +N}{2}\right) \left( \mathrm {\Gamma }\left( \frac{\eta }{2}\right) \right) ^{N}\left( 1+\eta ^{-1}\varvec{u'}\varvec{R}^{-1}\varvec{u}\right) ^{-\left( \eta +N\right) /2}}{\sqrt{|\varvec{R}|}\left( \mathrm {\Gamma }\left( \frac{\eta +N}{2}\right) \right) ^{N}\mathrm {\Gamma }\left( \frac{\eta }{2}\right) \prod _{i=1}^{N}\left( 1+\frac{u_{i}^{2}}{\eta }\right) ^{-\left( \eta +1\right) /2}}. \end{aligned}$$(15)For more details on the Student t-copula, see Demarta and McNeil (2005).
More specifically, the log-likelihood function \(LL_{V}\left( \cdot \right) \) in Eq. (16) is described as
$$\begin{aligned} LL_{V}\left( \varvec{\theta }^{D},\ \varvec{\theta }^{AG}\right)= & {} \sum _{t=1}^{T} \left( \sum _{i=1}^{N} log\left( \frac{1}{\sqrt{h_{i{\cdot }t}}}f_{i{\cdot }t}\left( \theta _{i}^{D},\ \theta _{i}^{AG} \ |\ z_{i{\cdot }t}\right) \right) \right) \nonumber \\&=\sum _{i=1}^{N} \left( \sum _{t=1}^{T} log\left( \frac{1}{\sqrt{h_{i{\cdot }t}}}f_{i{\cdot }t}\left( \theta _{i}^{D},\ \theta _{i}^{AG} \ |\ z_{i{\cdot }t}\right) \right) \right) \nonumber \\&=\sum _{i=1}^{N} LL_{V_{i}}\left( \theta _{i}^{D},\ \theta _{i}^{AG}\ | \ \varvec{z}_{i} \right) \end{aligned}$$(17)where \(f\left( \cdot \right) \) is the density function of \(z_{i}\) (one of normal, Student t, and skew t). Likewise, the log-likelihood function \(LL_{R}\left( \cdot \right) \) is described as
$$\begin{aligned} LL_{R}\left( \varvec{R}_{t},\ \eta \right)= & {} \sum _{t=1}^{T} log\left( c^{S_t}\left( \varvec{R}_{t},\ \eta \ | \ u_{1{\cdot }t}, \ldots , u_{N{\cdot }t}\right) \right) \nonumber \\&=\sum _{t=1}^{T} log\left( c^{S_t}\left( \mathrm {diag}\left( \varvec{M}_{t}\right) ^{-\frac{1}{2}}\varvec{M}_{t}\mathrm {diag}\left( \varvec{M}_{t}\right) ^{-\frac{1}{2}},\ \eta \ | \ u_{1{\cdot }t}, \ldots , u_{N{\cdot }t}\right) \right) \end{aligned}$$(18)where \(u_{i{\cdot }t}=F_{i}\left( r_{i{\cdot }t}\right) \) as described in Sect. 2.3; \(\varvec{M}_{t}\) depends on two types of parameters \(\left( \varvec{a},\ \varvec{b}\right) \) as defined in Eq. (6).
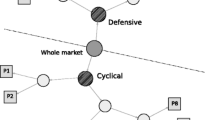
The dataset was updated from the one used in Isogai (2014); the grouping result is almost the same as the previous one.
The Perron–Frobenius theorem ensures that the eigenvector centrality measure takes a positive number. This theorem ensures that there is a unique eigenvector of matrix \(\varvec{A}\) with the largest positive eigenvalue; further, the eigenvector is positive and any non-negative eigenvector of \(\varvec{A}\) is a positive multiple of the vector, on condition that \(\varvec{A}\) is a non-negative regular matrix.
The 20 largest values were used by balancing the coverage of stocks in the universe and the complexity of the parameter estimation.
Engle (2001) discussed the technical difficulties associated with testing the null of constant correlation against an alternative of dynamic correlation. More recently, McCloud and Hong (2011) proposed a specification test for the constant and dynamic structures of conditional correlations, which is based on a generalized spectrum approach.
The model selection and parameter estimation results as well as goodness of fit test results are available as a supplementary note.
We used the R (http://cran.r-project.org/) package “rmgarch” (Ghalanos 2014) for the parameter estimation.
The values of \(a_{1}+b_{1}+b_{2}\) are all below 1, which indicates that the condition of Eq. (8) is satisfied.
The length of the corresponding eigenvector is normalized to one for all eigenvalues, since a symmetrical and positive definite matrix \(\varvec{R}_{t}\) has orthonormal eigenvectors.
The value of \(\beta \) depends on the assumption of the correlation matrix structure: \(\beta =1\) for the Gaussian orthogonal ensemble, \(\beta =2\) for the Gaussian unitary ensemble, and \(\beta =4\) for the Gaussian symplectic ensemble.
For more exact and complete definitions, see Tracy and Widom (1996).
We use R package “RMTstat” to calculate the density and quantiles of the Tracy–Widom and Mar\(\breve{c}\)enko–Pastur distributions.
EV2 is only meaningful in \(\mathrm {G_{L}}\) (one of the defensive groups), including Electric Power and Gas. \(\mathrm {G_{G}}\) (one of the defensive groups), including Banks, has the largest largest of EV1, which implies very strong correlations in regional banks.
The stock prices of some construction companies in \(\mathrm {G_{F}}\) showed an unusual pattern after the Great Earthquake; sharp increases were partially observed, which seemingly contributed to the lower correlation intensity at that time.
Note that because the sharp rise in volatility was slightly delayed after the Lehman collapse, whereas it occurred immediately after the Great Earthquake, this lag might overemphasize the changes after the latter event.
References
Aielli, G. P., & Caporin, M. (2013). Fast clustering of GARCH processes via Gaussian mixture models. Mathematics and Computers in Simulation, 94, 205–222.
Billio, M., Caporin, M., & Gobbo, M. (2006). Flexible dynamic conditional correlation multivariate GARCH models for asset allocation. Applied Financial Economics Letters, 2(02), 123–130.
Bollerslev, T. (1990). Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model. The Review of Economics and Statistics, 72(3), 498–505.
Demarta, S., & McNeil, A. J. (2005). The t copula and related copulas. International Statistical Review, 73(1), 111–129.
Engle, R. (2002). Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics, 20(3), 339–350.
Engle, R., & Kelly, B. (2012). Dynamic equicorrelation. Journal of Business & Economic Statistics, 30(2), 212–228.
Engle, R., & Sheppard, K. (2001). Theoretical and empirical properties of dynamic conditional correlation multivariate GARCH. National Bureau of Economic Research w8554.
Fernández, C., & Steel, M. F. J. (1998). On bayesian modeling of fat tails and skewness. Journal of the American Statistical Association, 93(441), 359–371.
Fortunato, S., & Barthélemy, M. (2007). Resolution limit in community detection. Proceedings of the National Academy of Sciences of the United States of America, 104(1), 36–41.
Ghalanos, A. (2014). rmgarch: Multivariate GARCH Models. R package version 1.2-8. http://cran.r-project.org/web/packages/rmgarch/index.html.
Girvan, M., & Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences of the United States of America, 99(12), 7821–6.
Isogai, T. (2014). Clustering of Japanese stock returns by recursive modularity optimization for efficient portfolio diversification. Journal of Complex Networks, 2(4), 557–584
Joe, H. (2005). Asymptotic efficiency of the two-stage estimation method for copula-based models. Journal of Multivariate Analysis, 94(2), 401–419.
Johnstone, I. M. (2001). On the distribution of the largest eigenvalue in principal components analysis. Annals of Statistics, 29(2), 295–327.
Jondeau, E., & Rockinger, M. (2006). The copula-GARCH model of conditional dependencies: An international stock market application. Journal of International Money and Finance, 25(5), 827–853.
Ledoit, O., & Wolf, M. (2003). Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. Journal of Empirical Finance, 10(5), 603–621.
Lee, T. H., & Long, X. (2009). Copula-based multivariate GARCH model with uncorrelated dependent errors. Journal of Econometrics, 150(2), 207–218.
Marčenko, V. A., & Pastur, L. A. (1967). Distribution of eigenvalues for some sets of random matrices. Sbornik: Mathematics, 1(4), 457–483.
McCloud, N., & Hong, Y. (2011). Testing the structure of conditional correlations in multivariate garch models: A generalized cross-spectrum approach. International Economic Review, 52(4), 991–1037.
Newman, M., & Girvan, M. (2004). Finding and evaluating community structure in networks. Physical Review E, 69(2), 026113.
Newman, M. E. (2004). Analysis of weighted networks. Physical Review E, 70(5), 056131.
Newman, M. E. J. (2006). Modularity and community structure in networks. Proceedings of the National Academy of Sciences of the United States of America, 103(23), 8577–82.
Newman, M. E. J. (2008). Mathematics of networks. In S. N. Durlauf & L. E. Blume (Eds.), The new Palgrave Encyclopedia of economics (2nd ed.). Basingstoke: Palgrave Macmillan.
Patton, A. J. (2006). Modelling asymmetric exchange rate dependence. International Economic Review, 47(2), 527–556.
Sklar, M. (1959). Fonctions de répartition à n dimensions et leurs marges. In Publ. Inst. Stat. 8, Université Paris, Paris (pp. 229–231).
Tracy, C. A., & Widom, H. (1994). Level-spacing distributions and the airy kernel. Communications in Mathematical Physics, 159(1), 151–174.
Tracy, C. A., & Widom, H. (1996). On orthogonal and symplectic matrix ensembles. Communications in Mathematical Physics, 177(3), 727–754.
Tracy, C. A., & Widom, H. (2009). The distributions of random matrix theory and their applications. In V. Sidoravicius (Ed.), New trends in mathematical physics (pp. 753–765). Dordrecht: Springer.
Author information
Authors and Affiliations
Corresponding author
Additional information
The views expressed here are solely those of the author and do not necessarily reflect those of the Bank of Japan.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Isogai, T. Analysis of Dynamic Correlation of Japanese Stock Returns with Network Clustering. Asia-Pac Financ Markets 24, 193–220 (2017). https://doi.org/10.1007/s10690-017-9230-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10690-017-9230-5