Abstract
Isomorphism and homomorphism are topics central to abstract algebra, but research on mathematicians’ views of these topics, especially with respect to sameness, remains limited. This study examines open response survey data from 197 mathematicians on how sameness could be helpful or harmful when studying isomorphism and homomorphism. Using thematic analysis, we examined whether sameness was viewed as helpful or harmful for isomorphism and homomorphism before examining rationales for those views. Making use of values of the mathematical community, we note that mathematicians saw conceptual and pedagogical benefits to connecting isomorphism and sameness, which connects to leveraging intuition and valuing ways of increasing understanding. Mathematicians’ concerns around using sameness largely revolved around the violation of the mathematical community’s idealized value of expressing a priori truth via a-contextual justifications. However, these concerns can be addressed through only targeted usage of sameness and explicit discussions around the utility and relevance of sameness. Implications include the importance of considering how interventions proposed by mathematics educators align with or provoke tension between values held by the mathematical community in order to mitigate or lean into those tensions and encourage fruitful dialogue between the mathematics and mathematics education communities.
Similar content being viewed by others
Data availability
n/a.
Code availability
n/a.
Notes
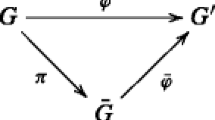
For reference: “An isomorphism \(\phi\) from a group \(G\) to a group \(\overline{G }\) is a one-to-one mapping (or function) from \(G\) onto \(\overline{G }\) that preserves the group operation. That is, \(\phi \left(ab\right)= \phi (a)\phi (b)\) for all \(a,b\) in \(G\). If there is an isomorphism from \(G\) onto \(\overline{G }\), we say that \(G\) and \(\overline{G }\) are isomorphic and write \(G\approx \overline{G }\)” (Gallian, 2009). A group homomorphism is a group isomorphism without the requirement of bijectivity.
References
Alibali, M. W., Knuth, E. J., Hattikudur, S., McNeil, N. M., & Stephens, A. C. (2007). A longitudinal examination of middle school students’ understanding of the equal sign and equivalent equations. Mathematical Thinking and Learning, 9(3), 221–247. https://doi.org/10.1080/10986060701360902
Anfara, V. A., Brown, K. A., & Mangione, T. L. (2002). Qualitative analysis on stage: Making the research process more public. Educational Researcher, 31(7), 28–38. https://doi.org/10.3102/0013189X031007028
Asghari, A. (2019). Equivalence: An attempt at a history of the idea. Synthese, 196, 4657–4677.
Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3(2), 77–101.
Dawkins, P. C., & Weber, K. (2017). Values and norms of proof for mathematicians and students. Educational Studies in Mathematics, 95, 123–142. https://doi.org/10.1007/s10649-016-9740-5
Dubinsky, E., Dautermann, J., Leron, U., & Zazkis, R. (1994). On learning fundamental concepts of group theory. Educational Studies in Mathematics, 27(3), 267–305.
Edwards, B., & Ward, M. (2008). The role of mathematical definitions in mathematics and in undergraduate mathematics courses. In M. Carlson & C. Rasmussen (Eds.), Making the connection: Research and teaching in undergraduate mathematics (pp. 221–230). Mathematical Association of America.
Gallian, J. (2009). Contemporary Abstract Algebra. Cengage Learning.
Hales, T. (2003). The Flyspeck Project Fact Sheet. Retrieved December 8, 2021 from https://code.google.com/archive/p/flyspeck/wikis/FlyspeckFactSheet.wiki
Hausberger, T. (2017). The (homo)morphism concept: Didactic transposition, meta-discourse, and thematisation. International Journal of Research in Undergraduate Mathematics Education, 3(3), 417–443. https://doi.org/10.1007/s40753-017-0052-7
Jett, C. (2013). Culturally responsive collegiate mathematics education: Implications for African American students. Interdisciplinary Journal of Teaching and Learning, 3(2), 102–116.
Jones, I., Inglis, M., Gilmore, C., & Dowens, M. (2012). Substitution and sameness: Two components of a relational conception of the equals sign. Journal of Experimental Child Psychology, 113, 166–176. https://doi.org/10.1016/j.jecp.2012.05.003
Knuth, E. J., Stephens, A. C., McNeil, N. M., & Alibali, M. W. (2006). Does understanding the equal sign matter? Evidence from solving equations. Journal for Research in Mathematics Education, 37(4), 297–312.
Lakoff, G., & Núñez, R. (1997). The metaphorical structure of mathematics: Sketching out cognitive foundations for a mind-based mathematics. In L. D. English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 21–89). Erlbaum.
Leron, U., Hazzan, O., & Zazkis, R. (1995). Learning group isomorphism: A crossroads of many concepts. Educational Studies in Mathematics, 29(2), 153–174.
Lew, K., Fukawa-Connelly, T. P., Mejía-Ramos, J. P., & Weber, K. (2016). Lectures in advanced mathematics: Why students might not understand what the mathematics professor is trying to convey. Journal for Research in Mathematics Education, 47(2), 162–198.
Mazur, B. (2008). When is one thing equal to some other thing? In B. Gold & R. A. Simons (Eds.), Proof and Other Dilemmas, MAA Spectrum, (pp. 221–241). Mathematical Association of America.
Melhuish, K. (2015). Determining what to assess: A methodology for concept domain analysis as applied to group theory. In T. Fukawa-Connelly, N. Infante, K. Keene, & M. Zandieh (Eds.), Proceedings of the 18th Annual Conference on Research in Undergraduate Mathematics Education (pp. 736–744). SIGMAA on RUME.
Melhuish, K., & Czocher, J. A. (2020). Division is pretty much just multiplication. For the Learning of Mathematics, 40(2), 38–43.
Melhuish, K., Lew, K., Hicks, M. D., & Kandasamy, S. S. (2020). Abstract algebra students’ evoked concept images for functions and homomorphisms. Journal of Mathematical Behavior, 60, 100806. https://doi.org/10.1016/j.jmathb.2020.100806
Mirin, A. (2018). Representational sameness and derivative. In Hodges, T. E., Roy, G. J., & Tyminski, A. M. (Eds.), Proceedings of the 40th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, (pp. 556–563). University of South Carolina & Clemson University.
Mirin, A., & Rupnow, R. (in press). Isomorphism and homomorphism in abstract algebra textbooks. Proceedings of the 24th Annual Conference on Research in Undergraduate Mathematics Education.
National Governors Association Center for Best Practices, Council of Chief State School Officers (2010). Common Core State Standards-Mathematics. National Governors Association Center for Best Practices, Council of Chief State School Officers.
Olsen, J., Lew, K., & Weber, K. (2020). Metaphors for learning and doing mathematics in advanced mathematics lectures. Educational Studies in Mathematics, 105, 1–17. https://doi.org/10.1007/s10649-020-09968-x
Rahim, M. H., & Olson, A. (1998). Qualitative patterns in plane geometry. Journal of Mathematical Behavior, 17(3), 373–389. https://doi.org/10.1016/S0364-0213(99)80069-X
Ronan, M. A. (2012). Modern algebra. Encyclopedia Britannica. Retrieved December 8, 2021 from https://www.britannica.com/science/modern-algebra
Rupnow, R. (2017). Students’ conceptions of mappings in abstract algebra. In A. Weinberg, C. Rasmussen, J. Rabin, M. Wawro, and S. Brown (Eds.), Proceedings of the 20th Annual Conference on Research in Undergraduate Mathematics Education Conference on Research in Undergraduate Mathematics Education, (pp. 259–273).
Rupnow, R. (2021). Conceptual metaphors for isomorphism and homomorphism: Instructors’ descriptions for themselves and when teaching. Journal of Mathematical Behavior, 62(2), 100867. https://doi.org/10.1016/j.jmathb.2021.100867
Saldaña, J. (2016). The coding manual for qualitative researchers. SAGE Publications Inc.
Turner, P., & Turner, S. (2009). Triangulation in practice. Virtual Reality, 13(3), 171–181. https://doi.org/10.1007/s10055-009-0117-2
Weber, K. (2004). Traditional instruction in advanced mathematics courses: A case study of one professor’s lectures and proofs in an introductory real analysis course. Journal of Mathematical Behavior, 23(2), 115–133.
Weber, K., & Alcock, L. (2004). Semantic and syntactic proof productions. Educational Studies in Mathematics, 56(2–3), 209–234.
Woods, C., & Weber, K. (2020). The relationship between mathematicians’ pedagogical goals, orientations, and common teaching practices in advanced mathematics. Journal of Mathematical Behavior, 59, 100792. https://doi.org/10.1016/j.jmathb.2020.100792
Zandieh, M., Ellis, J., & Rasmussen, C. (2016). A characterization of a unified notion of mathematical function: The case of high school function and linear transformation. Educational Studies in Mathematics, 95(1), 21–38. https://doi.org/10.1007/s10649-016-9737-0
Zazkis, R., & Leron, U. (1991). Capturing congruence with a turtle. Educational Studies in Mathematics, 22(3), 285–295.
Acknowledgements
This research was funded by a Northern Illinois University Research and Artistry Grant to Rachel Rupnow, grant number RA20-130. We also thank the editor and reviewers for their helpful comments on earlier drafts of the manuscript.
Funding
This project was funded by the Northern Illinois University Division of Research and Innovation Partnerships through a Research and Artistry grant, grant number RA20-130.
Author information
Authors and Affiliations
Contributions
The study conception, funding acquisition, and data collection were performed by Rachel Rupnow. The analysis was performed by Rachel Rupnow and Peter Sassman. The first draft of the manuscript was written by Rachel Rupnow and Peter Sassman. Both authors contributed to reviewing and editing the manuscript and read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval
This study has been approved by the Northern Illinois University Institutional Review Board, HS20-0306.
Consent to participate
n/a.
Consent for publication
n/a.
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Rupnow, R., Sassman, P. Sameness in algebra: views of isomorphism and homomorphism. Educ Stud Math 111, 109–126 (2022). https://doi.org/10.1007/s10649-022-10162-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10649-022-10162-4