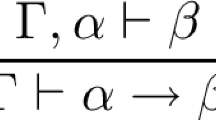Abstract
A non-classical subsystem of orthomodular quantum logic is proposed. This system employs two basic operations: the Sasaki hook as implication and the and-then operation as conjunction. These operations successfully satisfy modus ponens and the deduction theorem. In other words, they form an adjunction in terms of category theory. Two types of semantics are presented for this logic: one algebraic and one physical. The algebraic semantics deals with orthomodular lattices, as in traditional quantum logic. The physical semantics is given as a procedure for deriving a final segment of a series of yes-no experiments.
Similar content being viewed by others
Notes
Some symbols and names used here have been changed from Nishimura’s original ones.
For a sequent with an empty left-hand side, let \(\alpha \) be \(\bot \rightarrow \bot \), and for a sequent with an empty right-hand side, let \(\beta \) be \(\bot \).
The term counterfactual may possibly cause unnecessary confusion to the reader. As is well known, quantum theory is understood to be context-dependent due to the Kochen-Specker theorem, so it is problematic to make naive arguments based on counterfactual definiteness, such as “What would the result be if we measured momentum instead of position?” In the present paper, the counterfactual proposition Y/X is actually a simple rephrasing of the following situation, as can be seen from the deduction theorem: “Whenever X outputs yes, Y also outputs yes.”
The concept of distance between states is introduced by the norm determined by the inner product of \({\mathcal {H}}\).
Some technical conditions are not mentioned here.
The steps to introduce and eliminate double negation using \(\lnot \lnot \)-1, \(\lnot \lnot \) -2 and Cut rules are omitted here to avoid complexity.
References
Birkhoff G, von Neumann J (1936) The logic of quantum mechanics. Ann Math 37(4):823–843
Dalla Chiara ML, Giuntini R (2002) Quantum logics. In: Gabbay DM, Guenthner F (eds) Handbook of Philosophical Logic, vol 6. Springer, Dordrecht
Finch P (1969) On the structure of quantum logic. J Symb Logic 34(2):275–282
Finch P (1970) Quantum logic as an implication algebra. Bull Aust Math Soc 2(1):101–106
Hardegree G (1974) The conditional in quantum logic. Synthese 29(1/4):63–80
Herman L, Marsden EL, Piziak R (1975) Implication connectives in orthomodular lattices. Notre Dame J Formal Logic 16(3):305–328
Heunen C, Jacobs B (2011) Quantum logic in dagger kernel categories. Electron Notes Theor Comp Sci 270(2):79–103
Jammer M (1974) The philosophy of quantum mechanics, the interpretations of quantum mechanics in historical perspective. Wiley, New York
Jauch JM (1968) Foundations of quantum mechanics. Addison-Wesley, NY
Lehmann D, Engesser K, Gabbay DM (2006) Algebras of measurements: the logical structure of quantum mechanics. Int J Theor Phys 45(4):698–723
Lehmann D (2008) A presentation of quantum logic based on an and then connective. J Logic Comput 18(1):59–76
Nishimura H (1980) Sequential method in quantum logic. J Symb Logic 45(2):339–352
Román L, Rumbos B (1991) Quantum logic revisited. Found Phys 21(6):727–734
Shimony A (1971) Filters with infinitely many components. Found Phys 1:325–328
Tokuo K (2019) Feasible computation based on quantum logic. SN Appl Sci 1:1255
Ying M (2015) A theory of computation based on quantum logic (I). Theor Comp Sci 344(2–3):134–207
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The author has no conflicts of interest to declare that are relevant to the content of this article
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
We provide a proof of Theorem 1.
Proof
Formulas of the proposed system which contain \(\bot \), \(\rightarrow \), or & will be identified with the formulas of GOM as follows:
-
\(\bot \equiv \lnot \alpha \wedge \alpha \).
-
\(\alpha \rightarrow \beta \equiv \lnot (\alpha \wedge \lnot (\alpha \wedge \beta ))\).
-
\( \alpha \& \beta \equiv \lnot (\lnot \alpha \wedge \beta )\wedge \beta \).
It should be pointed out in advance that modus ponens in a single sequent form, i.e. \((\alpha \rightarrow \beta )\wedge \alpha \vdash \beta \), holds in GOM, as shown in the following diagram:Footnote 6

From this and the following identities, we can immediately see that modus ponens also holds for the combination of \(\rightarrow \) and & in GOM: \( (\alpha \rightarrow \beta ) \& \alpha = \lnot (\alpha \wedge \lnot (\alpha \wedge \beta )) \& \alpha =\lnot ((\alpha \wedge \lnot (\alpha \wedge \beta ))\wedge \alpha )\wedge \alpha =\lnot (\alpha \wedge \lnot (\alpha \wedge \beta ))\wedge \alpha =(\alpha \rightarrow \beta )\wedge \alpha \).
Axioms
-
Axiom-1. For each formula \(\alpha \), \(\alpha \vdash \alpha \) is an axiom of GOM.
-
Axiom-2.

Rules
-
Weakening-1, Weakening-2 and Cut . We can simply apply Weakening and Cut rules of GOM.
-
\(\rightarrow \) -1. Using modus ponens and&-2 rule, we have:

-
\(\rightarrow \) -2. Using modus ponens and&-1 rule , we have:

-
&-1. We can simply apply \(\wedge \) -1R rule of GOM.
-
&-2. Using &-1 rule, we have:

Identities
-
&-idempotency. Since we can prove \( \alpha \& \alpha \vdash \alpha \) and \( \alpha \vdash \alpha \& \alpha \) in GOM, we are justified in regarding \( \alpha \& \alpha \) and \(\alpha \) as identical.
-
Double Negation. Since we can prove \(\alpha \rightarrow \bot \vdash \lnot \alpha \) and \(\lnot \alpha \vdash \alpha \rightarrow \bot \) in GOM, we are justified in regarding \(\alpha \rightarrow \bot \) and \(\lnot \alpha \) as identical. Then, by using \(\lnot \lnot \)-1 and \(\lnot \lnot \) -2 rules of GOM, we are justified in regarding \((\alpha \rightarrow \bot )\rightarrow \bot \) and \(\alpha \) as identical. \(\square \)
Rights and permissions
About this article
Cite this article
Tokuo, K. Implicational quantum logic. Axiomathes 32 (Suppl 2), 473–483 (2022). https://doi.org/10.1007/s10516-021-09614-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10516-021-09614-y