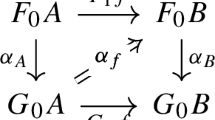Descent for internal multicategory functors

Abstract

We give sufficient conditions for effective descent in categories of (generalized) internal multicategories. Two approaches to study effective descent morphisms are pursued. The first one relies on establishing the category of internal multicategories as an equalizer of categories of diagrams. The second approach extends the techniques developed by Ivan Le Creurer in his study of descent for internal essentially algebraic structures.

1 Introduction

Let ${\mathcal {B}}$ be a category and $p :x \rightarrow y$ a morphism in ${\mathcal {B}}$ such that pullbacks along p exist. We say that p is an effective descent (descent) morphism whenever the change-of-base functor

$$\begin{aligned} p^*:{\mathcal {B}} \downarrow y \rightarrow {\mathcal {B}} \downarrow x \end{aligned}$$

is monadic (premonadic). The main subject of this note, the study of effective descent morphisms, is at the core of Grothendieck Descent Theory (see e.g. [12, 13]) and its applications (see, for instance, [2]).

Except for the case of locally cartesian closed categories, the full characterization of effective descent morphisms is far from trivial in general. The topological descent case is the main example of such a challenging problem (see the characterization in [18] and the reformulation in [5]).

The notion of $(T,{\mathcal {V}})$-categories, introduced in [10], generalizes both enriched categories and various notions of spaces. By studying effective descent morphisms in categories of $(T,{\mathcal {V}})$-categories, Clementino and Hofmann were able to give further descent results and understanding in various contexts, including, for instance, the reinterpretation of the topological results mentioned above and many other interesting connections (see, for instance, [6,7,8,9]).

On one hand, since they were mainly concerned with topological results, their study focused on the case where ${\mathcal {V}}$ is a quantale, and there is no obvious way to generalize their approach to more general monoidal categories ${\mathcal {V}}$. On the other hand, their work, together with the characterization of effective descent morphisms for the category of internal categories (see [12, Section 6] and [15]), have raised interest in further studying effective descent morphisms in categories of generalized categorical structures.

With this in mind, [17, Lemma 9.10] showed that we can embed the category of ${\mathcal {V}}$-enriched categories (with ${\mathcal {V}}$ lextensive) in the category of internal categories in ${\mathcal {V}}$. From this embedding, [17, Theorem 1.6] provides sufficient conditions for effective descent morphisms in ${\mathcal {V}}$-categories. However, the literature still lacks results for $(T,{\mathcal {V}})$-categories for a non-trivial T and an extensive ${\mathcal {V}}$.

The present note is part of a project which aims to study descent and Janelidze-Galois theory within the realm of generalized multicategories and other categorical structures. The first aim of this project consists of studying effective descent morphisms in categories of generalized multicategories.

While the definition of $(T,{\mathcal {V}})$-categories generalizes that of enriched categories, the definitions of internal T-multicategories in ${\mathcal {B}}$, for T a (cartesian) monad and ${\mathcal {B}}$ with pullbacks, introduced in [3, p. 8] and [11, Definition 4.2], generalize the notion of internal categories. Following this viewpoint and the approach of [17, Theorem 1.6], in order to study effective descent morphisms between more general $(T,{\mathcal {V}})$-categories, the first step is to study effective descent morphisms of categories of internal T-multicategories, which is the aim of the present paper.

The main contributions of our present work consist of two approaches to the problem of finding effective descent morphisms between internal multicategories. We explain, below, the key ideas of our first approach, which is the main subject of Section 4.

As a special case of [17, Theorem 9.2] (see Proposition 4.1), given a pseudo-equalizer (iso-inserter)

of categories with pullbacks and pullback preserving functors, p is of effective descent whenever FIp is of descent and Ip is of effective descent. Therefore, whenever (effective) descent morphisms in ${\mathcal {C}}$ and ${\mathcal {D}}$ are well-understood, we find tractable, sufficient conditions for effective descent in ${{\,\mathrm{{\textsf{PsEq}}}\,}}(F,G)$.

We establish the category ${\textsf{Cat}}(T, {\mathcal {B}})$ of internal T-multicategories in ${\mathcal {B}}$ as an equalizer consisting of a category of models of a finite limit sketch and categories of diagrams (Lemma 3.1), which is fully embedded in the corresponding pseudo-equalizer (Theorem 3.3). Since descent in categories of models of a finite limit sketch were studied in [15, Section 3.2], and categories of diagrams are well-understood, we obtain sufficient conditions for effective descent in the pseudo-equalizer by the result mentioned above (Lemma 4.3).

Finally, we find that the embedding of ${\textsf{Cat}}(T, {\mathcal {B}})$ into the pseudo-equalizer reflects effective descent morphisms (Lemma 4.4), getting, then, our first result. Namely, a functor p of internal T-multicategories is effective for descent whenever

• $Tp_1$ is an effective descent morphism in ${\mathcal {B}}$,

• $Tp_2$ is a descent morphism in ${\mathcal {B}}$,

• $p_3$ is an almost descent morphism in ${\mathcal {B}}$,

where $p_i$ is the component of p between the objects of i-tuples of composable morphisms (Theorem 4.5).

Our second approach to the problem is presented in Section 5, which extends the work of [15] on effective descent morphisms between internal structures. We observe that the same techniques employed in Le Creurer’s work can be applied to the “sketch” of internal T-multicategories. With these techniques, we were able to refine our result on effective descent morphisms. We prove that functors p such that

• $p_1$ is an effecive descent morphism in ${\mathcal {B}}$,

• $p_2$ is a descent morphism in ${\mathcal {B}}$,

• $p_3$ is an almost descent morphism in ${\mathcal {B}}$,

are effective descent morphisms in ${\textsf{Cat}}(T,{\mathcal {B}})$.

The techniques exploited in Section 5 proved to be more suitable to our context of internal structures. However, the approach given there cannot be trivially applied to other generalized (enriched) categorical structures. Thus, Section 4 has expository value and its techniques are especially relevant to our future work in descent theory of generalized (enriched) categorical structures.

After fixing some notation on Section 1, we recall some basic aspects on effective descent morphisms in Section 2. Then, we study the equalizer that gives the category of internal T-multicategories and its corresponding pseudo-equalizer in Section 3. Afterwards, we discuss each approach to our main problem in the two subsequent sections. We end the paper with a discussion of examples of cartesian monads and internal multicategories.

2 Preliminaries

Let $J :{\mathcal {B}} \rightarrow {\mathcal {C}}$ be a diagram with a limit $(\lim J, \lambda )$. For any cone $\gamma _b :x \rightarrow Jb$, there exists a unique morphism $f :x \rightarrow \lim J$ such that $\gamma _b = \lambda _b \circ f$ for all b in ${\mathcal {B}}$. We denote f as $(\gamma _b)_{b \in {{\,\mathrm{{\textsf{ob}}}\,}}\, {\mathcal {B}}}$. As an example, let ${\mathcal {B}}$ be a category with pullbacks, and ${\mathscr {C}}$ an internal category. The object of pairs of composable morphisms is given by the pullback:

Thus, if we have morphisms $g :X \rightarrow {\mathscr {C}}_1$ and $f :X \rightarrow {\mathscr {C}}_1$ with $d_1 \circ g = d_0 \circ f$, we write $(g,\, f)$ for the uniquely determined morphism $X \rightarrow {\mathscr {C}}_2$. Furthermore, we denote the internal composition by $g \bullet f = d_1 \circ (g,\, f)$, where $d_1 :{\mathscr {C}}_2 \rightarrow {\mathscr {C}}_1$ is the composition morphism. Likewise, we can talk about tuples of composable morphisms, an idea we apply to T-multicategories.

Another remark on notation: in a category ${\mathcal {B}}$ with a choice of pullbacks, we write

for the chosen pullback of f along p. It is clear that the change-of-base $p^* :{\mathcal {B}} \downarrow y \rightarrow {\mathcal {B}} \downarrow x$ defines a functor right adjoint to $p_! :{\mathcal {B}} \downarrow x \rightarrow {\mathcal {B}} \downarrow y$ with counit $\epsilon$. For a morphism $h :f \rightarrow g$ in ${\mathcal {B}} \downarrow y$ (that is, $f = g \circ h$), write $p^*_h$ for the unique morphism $p^*f \rightarrow p^*g$ such that $\epsilon _g \circ p^*_h = h \circ \epsilon _f$.

3 Effective descent morphisms

We recall some known facts about effective descent morphisms. In a category ${\mathcal {B}}$ with chosen pullbacks along p, the category ${\textsf{Desc}}(p)$ of descent data for a morphism $p :x \rightarrow y$ in ${\mathcal {B}}$ is defined as the category of algebras for the monad $p^*p_!$. Explicitly, objects are pairs of morphisms $(a:w \rightarrow x, \gamma :v \rightarrow w)$ satisfying

• $p^*(p\circ a) = a \circ \gamma$, that is, $\gamma$ is a morphism $p^*(p\circ a) \rightarrow a$ in ${\mathcal {B}} \downarrow x$,

• $\gamma \circ p^*_{\epsilon _{p \circ a}} = \gamma \circ p^*_\gamma$, the multiplication law (note that $p \circ a \circ \gamma = p \circ p^*(p \circ a)$, so that we may apply $p^*$),

• $\gamma \circ (a,{\textsf {id}}) = {\textsf {id}}$, the unit law, where $(a,{\textsf {id}})$ is the unique morphism such that $a = p^*(p\circ a) \circ (a,{\textsf {id}})$ and ${\textsf {id}}= \epsilon _{p \circ a} \circ (a,{\textsf {id}})$.

A morphism $(a,\gamma ) \rightarrow (b,\theta )$ of descent data is a morphism f with $a = b \circ f$ such that $f \circ \gamma = \theta \circ p^*_f$.

Further recall the Eilenberg-Moore factorization of $p^*$:

Here, ${\mathcal {U}}^p$ is the forgetful functor, and ${\mathcal {K}}^p$ is commonly denoted the comparison functor. We say a morphism p is

• an almost descent morphism if ${\mathcal {K}}^p$ is faithful,

• a descent morphism if ${\mathcal {K}}^p$ is fully faithful,

• an effective descent morphism if ${\mathcal {K}}^p$ is an equivalence.

By the Bénabou-Roubaud theorem (originally proven in [1], see, for instance, [13, p. 258] or [17, Theorem 7.4 and Theorem 8.5] for generalizations), this is equivalent to the classical formulation of the descent category w.r.t. the basic (bi)fibration.

As a consequece of Beck’s monadicity theorem, we may characterize (almost) descent morphisms (also check [15, Corollary 0.3.4] and [12, Theorem 3.4]):

Proposition 2.1

In a category ${\mathcal {B}}$ with finite limits, pullback-stable epimorphisms are exactly the almost descent morphisms, and pullback-stable regular epimorphisms are exactly the descent morphisms.

Proof

Let $p :x \rightarrow y$ be a morphism in ${\mathcal {B}}$. ${\mathcal {K}}^p$ is (fully) faithful if and only if $\epsilon$ is a pointwise (regular) epimorphism (in ${\mathcal {B}} \downarrow y$), which happens if and only if p is a universal (regular) epimorphism in ${\mathcal {B}} \downarrow y$, as $\epsilon$ is given pointwise by pullback of p.

Since ${\mathcal {B}}$ has a terminal object, the forgetful functor ${\mathcal {B}}/y \rightarrow {\mathcal {B}}$ has a right adjoint, hence it preserves colimits. $\square$

Thus, once we have a pullback-stable regular epimorphism p, it is natural to take an interest in studying the image of ${\mathcal {K}}^p$. To do so, we make the following elementary observation. Since we have defined descent data as algebras, we restrict our attention to this context. It should be noted, however, that the result holds in much more general contexts, and hence its applicability in descent arguments does not depend on the Bénabou-Roubaud theorem.

Lemma 2.2

Let $( L\dashv U, \epsilon , \eta ) :{\mathcal {A}} \rightarrow {\mathcal {B}}$ be an adjunction and let T be the induced monad. An algebra $(a, \gamma )$ is in the image of the Eilenberg-Moore comparison ${\mathcal {K}}^T :{\mathcal {A}} \rightarrow T \text {-}{{\textsf{Alg}} }$ if, and only if, a is in the image of U and

$$\begin{aligned} \epsilon _w \circ L\gamma = \epsilon _w \circ \epsilon _{LUw}. \end{aligned}$$

(1)

where w is an object such that $a = Uw$.

Proof

The algebra ${\mathcal {K}}^Tw$ satisfies (1) by naturality. Conversely, if an algebra $(Uw, \gamma )$ satisfies (1), then

$$\begin{aligned} \gamma = U\epsilon _w \circ \eta _{Uw} \circ \gamma = U\epsilon _w \circ UL\gamma \circ \eta _{ULUw} = U\epsilon _w \circ U\epsilon _{LUw} \circ \eta _{ULUw} = U\epsilon _w \end{aligned}$$

Hence $(Uw, \gamma ) = {\mathcal {K}}^Tw$. $\square$

As a corollary, we get a fairly commonly used result in proofs about effective descent morphisms. It has been, sometimes, implicitly assumed in the literature. The instance of Le Creurer’s argument in Proposition 3.2.4, where he implicitly uses this result, is of particular interest for our work.

Corollary 2.3

${\mathcal {K}}^p$ is essentially surjective if and only if, for all descent data $(a,\gamma )$, there is f such that $p^*f \cong a$ and $\epsilon _f \circ \gamma = \epsilon _f \circ \epsilon _{p\circ a}$.

We finish this section recalling the following classical descent result (see [13, 2.7], [12, 3.9]):

Proposition 2.4

Let $U :{\mathcal {C}} \rightarrow {\mathcal {D}}$ be a fully faithful, pullback-preserving functor, and let p be a morphism in ${\mathcal {C}}$ such that Up is effective for descent. Then p is effective for descent if and only if for all pullback diagrams of the form

there exists an isomorphism $Uy \cong z$ for y an object of $\mathcal C$.

The following consequence is of particular interest:

Corollary 2.5

Let $U :{\mathcal {C}} \rightarrow {\mathcal {D}}$ be a fully faithful, pullback-preserving functor. If there exists $z \cong Uy$ whenever there is an effective descent morphism $g :Ux \rightarrow z$, then U reflects effective descent morphisms.

Proof

Suppose (2) is a pullback square. If Up is an effective descent morphism, then so is $f^*(Up) :Ux \rightarrow z$ by pullback-stability. By hypothesis, we have $z \cong Uy$, whence we conclude that p is effective for descent by Proposition 2.4. $\square$

4 Multicategories and pseudo-equalizers

Recall that a monad $T = (T,m,e)$ is cartesian if T preserves pullbacks and the naturality squares of m and e are pullbacks.

As defined in [11], for T a cartesian monad on a category $\mathcal B$ with pullbacks, a T-multicategory internal to ${\mathcal {B}}$ is a monad in the bicategory ${\textsf{Span}}_T({\mathcal {B}})$, and a functor between two such T-multicategories is a monad morphism considering the usual proarrow equipment ${\mathcal {B}}\rightarrow {\textsf{Span}}_T({\mathcal {B}})$; these define the category ${\textsf{Cat}}(T, {\mathcal {B}})$. Explicitly, a T-multicategory is given by an object $x_0$ of ${\mathcal {B}}$, together with a span

and two morphisms, given by dashed arrows below

which make the triangles commute, where

is a pullback diagram. Moreover, this data is required to satisfy certain identity and associativity conditions, which we will proceed to specify.

Following the terminology of Section 1, we say that a pair $g :a \rightarrow x_1$, $f :a \rightarrow Tx_1$ is composable if $d_1g = (Td_0)f$, we write $(g,f) :a \rightarrow x_2$ for the uniquely defined morphism, and we let $g \bullet f = d_1(g,f)$. Likewise, define $k \bullet _T h = (Td_1)(k,h)$ for $k :a \rightarrow Tx_1$ and $h :a \rightarrow TTx_1$ such that $(Td_1)k = (TTd_0)h$ (T-composable).

The identity properties of the monad guarantee that $1_{d_0f} \bullet (e \circ f) = f = f \bullet 1_{d_1f}$, and the associativity property guarantees that $h \bullet (g \bullet _T f) = (h \bullet g) \bullet (m \circ f)$, where we are implicitly given the following pullback diagram

for $h :a \rightarrow x_1$, $g :a \rightarrow Tx_1$ and $f :a \rightarrow TTx_1$ such that $h,\,g$ are composable and $g,\,f$ are T-composable. Moreover, a functor $p :x \rightarrow y$ between internal T-multicategories is given by a pair of morphisms $p_0 :x_0 \rightarrow y_0$ and $p_1 :x_1 \rightarrow y_1$ such that $d_i \circ p_1 = (T^ip_0) \circ d_i$ for $i=0,1$, $1_{p_0} = p_1 1$ and $p_1g \bullet p_1f = p_1(g\bullet f)$.

Going back to an internal description, we may denote

• $s_0 = ({\textsf {id}},\, Ts_0 \circ d_1) :x_1 \rightarrow x_2$,

• $s_1 = (s_0 \circ d_0,\, e) :x_1 \rightarrow x_2$,

• $d_1 = (d_0 \circ d_0,\, Td_1 \circ d_3)$,

• $d_2 = (d_1 \circ d_0,\, m \circ Td_2 \circ d_3)$,

so the above data can be organized in the following diagram

which is similar to [3, Figure 1]. In fact, one may define T-multicategory as a diagram satisfying certain relations, a description particularly suitable for our techniques in Section 4. First, we let ${\mathcal {S}}$ be the (finite limit) sketch given by the following graph

with relations resembling cosimplicial identities

• $s_1 \circ s_0 = s_0 \circ s_0 :x_0 \rightarrow x_2$,

• $d_{1+i} \circ s_i = e_i :x_i \rightarrow x'_i$,

• $d_i \circ s_j = {\textsf {id}}:x_i \rightarrow x_i$,

• $d_2 \circ s_0 = s_0' \circ d_1 :x_1 \rightarrow x'_1$,

• $d_0 \circ s_1 = s_0 \circ d_0 :x_1 \rightarrow x_1$,

• $d'_0 \circ s'_0 = {\textsf {id}}:x'_0 \rightarrow x'_0$,

• $d_{1+i} \circ d_{1+i} = m_i \circ d'_{1+i} \circ d_{2+i} :x_{2+i} \rightarrow x'_i$,

• $d_{1+i} \circ d_0 = d_0' \circ d_{2+i} :x_{2+i} \rightarrow x_i$,

• $d'_j \circ d_{2+i} = d_{1+i} \circ d_j :x_{2+i} \rightarrow x'_i$,

• $d_0 \circ d_1 = d_0 \circ d_0 :x_2 \rightarrow x_0$,

• $d_j \circ d_{1+i} = d_i \circ d_j :x_3 \rightarrow x_1$,

• $d'_1 \circ d_0' = d_0'' \circ d_2' :x_2' \rightarrow x_0''$,

• $d'_0 \circ d'_1 = d'_0 \circ d'_0 :x'_2 \rightarrow x_0'$,

and limit cones

with $i=0,1$ and $j \le i$. Abusing notation, we also denote by ${\mathcal {S}}$ the category generated by the graph (3) and the given relations. Writing ${\textsf{Mod}}({\mathcal {S}}, {\mathcal {B}})$ for the category of ${\mathcal {B}}$-models of ${\mathcal {S}}$, we have:

Lemma 3.1

For a cartesian monad (T, m, e) on a category ${\mathcal {B}}$ with pullbacks, ${{\textsf{Cat}} }(T,B)$ is given as the equalizer of the following composite of pullback-preserving functors:

Moreover, ${{\textsf{Cat}} }(T, {\mathcal {B}})$ has pullbacks and the canonical functor ${{\textsf{Cat}} }(T,{\mathcal {B}}) \rightarrow {{\textsf{Mod}} }({\mathcal {S}}, {\mathcal {B}})$ preserves them.

Remark 3.2

It might seem superfluous to require the right diagram of (4) to be a pullback, as the equalizer condition will force $x'_i = Tx_i$ and $x''_i = TTx_i$, and since T preserves pullbacks, the pullback condition for the aforementioned diagram is already guaranteed.

Moreover, omitting this apparently redundant diagram, an analogous version of Lemma 3.1 would describe Burroni’s notion of T-multicategories (check [3], where this extra pullback condition is not required), even when T is not cartesian, or even pullback-preserving.

In spite of the above reasons, this requirement is justified by the sharper results we obtain about effective descent in ${\textsf{Mod}}({\mathcal {S}}, {\mathcal {B}})$ (see Proposition 4.2), and consequently, in ${\textsf{Cat}}(T, {\mathcal {B}})$ as well (see Theorem 4.5).

Note that the inclusion ${\textsf{Mod}}({\mathcal {S}}, {\mathcal {B}}) \rightarrow [{\mathcal {S}}, {\mathcal {B}}]$ is an iso-inserter of categories of diagrams, thus it creates limits.

The categories ${\mathcal {S}}_I$, ${\mathcal {S}}_T$, ${\mathcal {S}}_{m_i}$, and $\mathcal S_{e_i}$ for $i=0,1$ are subcategories of ${\mathcal {S}}$, respectively given by

and write $S^*_I$, $S^*_T$, $S^*_{m_i}$, $S^*_{e_i}$, for the restriction functors. Also write $x_0^*$ and $x_1^* :[\mathcal S,{\mathcal {B}}] \rightarrow {\mathcal {B}}$ for the projections. With these, $S^*_-$, and $\Phi$ are the uniquely determined functors given by the following

where $T_*$, ${\hat{m}}$ and ${\hat{e}}$ are the functors induced by the monad T. Note that these preserve pullbacks exactly when T is cartesian.

Note that, in general, the equalizer is a full subcategory of the pseudo-equalizer: for functors $F, G :{\mathcal {C}} \rightarrow {\mathcal {D}}$, the category ${{\,\mathrm{{\textsf{PsEq}}}\,}}(F,G)$ is the category whose objects are pairs $(c,\phi )$ where c is an object of ${\mathcal {C}}$ and $\iota :Fy \rightarrow Gy$ is an isomorphism, and morphisms $(c,\phi ) \rightarrow (d,\psi )$ are morphisms $f :c \rightarrow d$ such that $Gf \circ \phi = \psi \circ Ff$. Thus, the full embedding may be given on objects by $x \mapsto (x,{\textsf {id}})$.

Henceforth, we denote

$$\begin{aligned} {\mathcal {P}} = {{\,\mathrm{{\textsf{PsEq}}}\,}}(S^*_- \circ I, \Phi \circ I). \end{aligned}$$

(6)

Lemma 3.3

The inclusion ${{\textsf{Cat}} }(T,{\mathcal {B}}) \rightarrow {\mathcal {P}}$ is full and preserves pullbacks.

Proof

The inclusion ${\textsf{Cat}}(T,{\mathcal {B}}) \rightarrow {\textsf{Mod}}({\mathcal {S}}, {\mathcal {B}})$ preserves pullbacks, which are then created by ${\mathcal {P}} \rightarrow {\textsf{Mod}}({\mathcal {S}}, {\mathcal {B}})$. $\square$

Given an object $(y,\iota )$ of ${\mathcal {P}}$, $\iota$ can be explicitly described as a family of isomorphisms making the appropriate squares commute:

Lemma 3.4

An object $(y,\iota )$ of ${\mathcal {P}}$ is isomorphic to a T-multicategory if and only if the following coherence conditions hold:

• (i) $\iota ^{m_i}_1 = \iota ^{e_i}_1 = \iota ^T_i$ for $i=0,1$,

• (ii) $T\iota ^T_i \circ \iota ^T_{3+i} = \iota ^{m_i}_0$, for $i=0,1$,

• (iii) $\iota _0^{e_i} = {\textsf {id}}$ for $i=0,1$,

Such an object $(y,\iota )$ satisfying these conditions is said to be coherent.

Proof

Given a coherent $(y,\iota )$, we define a T-multicategory ${\hat{y}}$ such that ${\hat{y}}_0 = y_0$, ${\hat{y}}_1 = y_1$, and we consider the span

so that we have ${\hat{d}}_1 = \iota ^T_0 \circ d_1$, ${\hat{d}}_0 = d_0$, and we let ${\hat{d}}_1 = d_1 :x_2 \rightarrow x_1$ and ${\hat{s}}_0 = s_0 :x_0 \rightarrow x_1$.

Consider the diagram for $i=0,1$:

The right square is a pullback because $\iota ^T_j$ is an isomorphism for $j=0,1,2$, and the left square is a pullback by definition, therefore the outer rectangle is a pullback as well.

Let ${\hat{d}}_0 = d_0 :y_{2+i} \rightarrow y_{1+i}$ and ${\hat{d}}_{2+i} = \iota ^T_{1+i} \circ d_{2+i} :y_{2+i} \rightarrow y_{1+i}$ for $i = 0,1$. We claim that every triangle commutes:

Of course, both right triangles commute by definition. Moreover, we have that the diagram

commutes by the naturality of $\iota$ and coherence of $(y,\iota )$.

Since $M \circ d'_1 \circ d_2 = d_1 \circ d_1$ by definition, the left triangle of (7) commutes. The left triangle of (8) also commutes, for we have $e = \iota ^{e_0}_1 \circ e_0$, $\iota ^{e_0}_1 = \iota ^T_0$ and $e_0 = d_1 \circ s_0$.

We claim it is possible to define

• ${\hat{s}}_0 = ({\textsf {id}}, Ts_0 \circ {\hat{d}}_1)$

• ${\hat{s}}_1 = (s_0 \circ d_0, e)$

• ${\hat{d}}_2 = (d_1 \circ d_0, m \circ T{\hat{d}}_2 \circ {\hat{d}}_3)$

• ${\hat{d}}_1 = (d_0 \circ d_0, Td_1 \circ {\hat{d}}_3)$

and in order to verify our claim, we must show that

• ${\hat{d}}_1 = Td_0 \circ Ts_0 \circ {\hat{d}}_1$,

• ${\hat{d}}_1 \circ s_0 \circ d_0 = Td_0 \circ e$,

• ${\hat{d}}_1 \circ d_1 \circ d_0 = Td_0 \circ m \circ T{\hat{d}}_2 \circ {\hat{d}}_3$,

• ${\hat{d}}_1 \circ d_0 \circ d_0 = Td_0 \circ Td_1 \circ {\hat{d}}_3$,

Since $d_0 \circ s_0$ is the identity, the first equation is satisfied. We have

$$\begin{aligned} \iota ^T_0 \circ d_1 \circ s_0 \circ d_0 = \iota ^{e_0}_1 \circ e_0 \circ d_0 = e \circ d_0 = Td_0 \circ e, \end{aligned}$$

which verifies the second. For the third and fourth, we have

$$\begin{aligned} \iota ^T_0 \circ d_1 \circ d_0 \circ d_0&= \iota ^T_0 \circ d'_0 \circ d_2 \circ d_0 \\&= Td_0 \circ \iota ^T_1 \circ d'_0 \circ d_3 \\&= Td_0 \circ Td_0 \circ \iota ^T_2 \circ d_3 \\&= Td_0 \circ Td_1 \circ {\hat{d}}_3, \\ Td_0 \circ m \circ T\iota ^T_1 \circ Td_2 \circ \iota ^T_2 \circ d_3&= m \circ TTd_0 \circ T\iota ^T_1 \circ Td_2 \circ \iota ^T_2 \circ d_3\\&= m \circ T\iota ^T_0 \circ Td'_0 \circ Td_2 \circ \iota ^T_2 \circ d_3\\&= m \circ T\iota ^T_0 \circ Td_1 \circ Td_0 \circ \iota ^T_2 \circ d_3\\&= m \circ T\iota ^T_0 \circ Td_1 \circ \iota ^T_1 \circ d'_0 \circ d_3\\&= m \circ T\iota ^T_0 \circ \iota ^T_3 \circ d'_1 \circ d_2 \circ d_0\\&= m \circ \iota ^{m_0}_0 \circ d'_1 \circ d_2 \circ d_0 \\&= \iota ^{m_0}_1 \circ m_0 \circ d'_1 \circ d_2 \circ d_0 \\&= \iota ^{m_0}_1 \circ d_1 \circ d_1 \circ d_0, \end{aligned}$$

as desired.

Recalling that the left square in (9) is a pullback for $i=0, 1$, it follows that $s_0, s_1 :x_1 \rightarrow x_2$ and $d_1, d_2 :x_3 \rightarrow x_2$ are given by $({\textsf {id}}, s'_0 \circ d_1)$, $(s_0 \circ d_0, e_1)$, $(d_1 \circ d_0, m_1 \circ d'_2 \circ d_3)$ and $(d_0 \circ d_0, d'_1 \circ d_3)$, respectively. But these are just ${\hat{s}}_0, {\hat{s}}_1, {\hat{d}}_1, {\hat{d}}_2$, respectively.

The converse is implied by the result that follows. $\square$

Theorem 3.5

If $f :(x,{\textsf {id}} ) \rightarrow (y,\iota )$ is a pointwise epimorphism in ${\mathcal {P}}$, then $(y,\iota )$ is coherent. Hence, $(y, \iota )$ is isomorphic to a T-multicategory.

Proof

A morphism $f :(x,{\textsf {id}}) \rightarrow (y,\iota )$ is a morphism $f :x \rightarrow y$ such that $Gf = \iota \circ Ff$, which translates to the following equations:

$$\begin{aligned} f_0&= \iota ^{e_0}_0 \circ f_0 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f'_0 = \iota ^T_0 \circ Tf_0 = \iota ^{m_0}_1 \circ Tf_0 = \iota ^{e_0}_1 \circ Tf_0 \\ f_1&= \iota ^{e_1}_0 \circ f_1 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f'_1 = \iota ^T_1 \circ Tf_1 = \iota ^{m_1}_1 \circ Tf_1 = \iota ^{e_1}_1 \circ Tf_1 \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f'_2 = \iota ^T_2 \circ Tf_2&\\ f''_0&= \iota ^T_3 \circ Tf'_0 = \iota ^{m_0}_0 \circ TTf_0&\\ f''_1&= \iota ^T_4 \circ Tf'_1 = \iota ^{m_1}_0 \circ TTf_1&\end{aligned}$$

and noting that $f_i, f'_i, f''_i$ all are epimorphisms for all i we recover the coherences; just note that $Tf_i$ and $TTf_i$ are epimorphisms as well, and that $Tf'_i = T\iota ^T_i \circ TTf_i$. $\square$

5 Descent via bilimits

Recall the pseudo-equalizer ${\mathcal {P}}$ defined in (6) from the previous section. We understand the effective descent morphisms of $\mathcal P$ via the effective descent morphisms of ${\textsf{Mod}}({\mathcal {S}}, {\mathcal {B}})$ by the following instance of [17, Theorem 9.2].

Proposition 4.1

Suppose that we have a pseudo-equalizer of categories and pullback-preserving functors

and let f be a morphism in the pseudo-equalizer. Then f is effective for descent whenever If is effective for descent and $FIf \cong GIf$ is a pullback-stable regular epimorphism.

Furthermore, by the work of [15], we are able to provide sufficient conditions for effective descent in ${\textsf{Mod}}({\mathcal {S}}, {\mathcal {B}})$ for ${\mathcal {B}}$ with finite limits:

Proposition 4.2

If a morphism p in ${{\textsf{Mod}} }({\mathcal {S}}, {\mathcal {B}})$ is such that

• $p_0, p_1, p'_0, p'_1, p''_0, p''_1$ are effective descent morphisms in ${\mathcal {B}}$,

• $p_2, p'_2$ are descent morphisms in ${\mathcal {B}}$,

• $p_3$ is an almost descent morphism in ${\mathcal {B}}$,

then p is an effective descent morphism in ${{\textsf{Mod}} }({\mathcal {S}}, {\mathcal {B}})$.

Proof

We refer the reader to Section 3.2 ibid if they wish to fill in the details. The sketch ${\mathcal {S}}$ may be given as an essentially algebraic theory with sorts $x_0$, $x_1$, $x_0'$, $x_1'$, $x_0''$, $x_1''$, partially defined operations $d_1 :x_1 \times x_1' \rightarrow x_1$, $d_1' :x'_1 \times x''_1 \rightarrow x'_1$, and equation $(d_1 \circ ({\textsf {id}},d_1), d_1 \circ (d_1,{\textsf {id}})) :x_1 \times x'_1 \times x''_1 \rightarrow x_1$, among other data and equations. Then apply Proposition 3.2.4 ibid. $\square$

With T cartesian, diagram (5) is a pseudo-equalizer, so we are under the hypothesis of Proposition 4.1. Therefore:

Lemma 4.3

A morphism p in ${\mathcal {P}}$ is effective for descent whenever p is effective for descent in ${{\textsf{Mod}} }({\mathcal {S}}, {\mathcal {B}})$ and $S^*_Xp$ is a descent morphism for each $X = T, m_0, m_1, e_0, e_1$.

In particular, if p satisfies the conditions in Proposition 4.2, then p is effective for descent in the pseudo-equalizer.

Proof

We observe that a morphism in a product of categories is of descent if and only if each component is a descent morphism. Moreover, pointwise (effective) descent in $[{\mathcal {S}}, {\mathcal {B}}]$ implies pointwise descent in $[{\mathcal {S}}_X, {\mathcal {B}}]$ for every X. Therefore, the result follows by Proposition 4.1. $\square$

By Lemma 3.3, we may apply the previous proposition to $U :{\textsf{Cat}}(T, {\mathcal {B}}) \rightarrow {\mathcal {P}}$. Consequently, we can show that:

Lemma 4.4

U reflects effective descent morphisms.

Proof

Since every effective descent morphism is an epimorphism, the result follows by Theorem 3.5 and Corollary 2.5. $\square$

Combining Lemmas 4.3 and 4.4 , we get our main result:

Theorem 4.5

For ${\mathcal {B}}$ with finite limits, let $p :x \rightarrow z$ be a T-multicategory functor internal to ${\mathcal {B}}$. If $Tp_1$ is an effective descent morphism, $Tp_2$ is a descent morphism and $p_3$ is an almost descent morphism in ${\mathcal {B}}$, then p is an effective descent morphism in ${{\textsf{Cat}} }(T,{\mathcal {V}})$.

Proof

By the results in Appendix A (observe that $Tp_1$ is a T-graph morphism), we guarantee that p is an effective descent morphism in ${\textsf{Mod}}({\mathcal {S}}, {\mathcal {B}})$. Now apply Theorem 4.4. $\square$

6 Descent via sketches

In this section, we extend the techniques of [15, Chapter 3] to give refined sufficient conditions for (effective) descent morphisms in ${\textsf{Cat}}(T,{\mathcal {B}})$ in the broader sense of Burroni; that is, without requiring T to be cartesian (though we require T to preserve kernel pairs for Theorem 5.3), while keeping the definition of T-multicategory intact. We highlight that given a functor $p :x \rightarrow y$ of internal multicategories, if $p_1$ is a pullback-stable (regular) epimorphism, or of effective descent, then so is $p_0$ by Lemma A.3.

Lemma 5.1

Let $p :x \rightarrow y$ be a functor of internal T-multicategories. If $p_1$ is an (pullback-stable) epimorphism in ${\mathcal {B}}$, then so is p in ${{\textsf{Cat}} }(T,{\mathcal {B}})$.

Proof

Given functors q, r such that $q \circ p = r \circ p$, we have $q_i \circ p_i = r_i \circ p_i$, and therefore $q_i = r_i$ for $i = 0,\, 1$, hence $q = r$, thus p is an epimorphism. Since pullbacks are calculated pointwise, p must be pullback-stable whenever $p_1$ is. $\square$

Lemma 5.2

Let p be a functor of internal T-multicategories. If

• $p_1$ is a (pullback-stable) regular epimorphism in ${\mathcal {B}}$,

• $p_2$ is an (pullback-stable) epimorphism in ${\mathcal {B}}$,

then p is a (pullback-stable) regular epimorphism in ${{\textsf{Cat}} }(T,{\mathcal {B}})$.

Proof

Consider the kernel pair r, s of p, and let $q :x \rightarrow z$ be a functor such that $q \circ r = q \circ s$. Then there exist unique morphisms $k_0$, $k_1$ such that $k_i \circ p_i = q_i$ for $i = 0,\, 1$. We claim these morphisms define a functor $y \rightarrow z$. We have

$$\begin{aligned} d_1 \circ k_1 \circ p_1&= d_1 \circ q_1 = Tq_0 \circ d_1 = Tk_0 \circ Tp_0 \circ d_1 = Tk_0 \circ d_1 \circ p_1 \\ d_0 \circ k_1 \circ p_1&= d_0 \circ q_1 = q_0 \circ d_0 = k_0 \circ p_0 \circ d_0 = k_0 \circ d_0 \circ p_1 \\ k_1 \circ d_1 \circ p_2&= k_1 \circ p_1 \circ d_1 = q_1 \circ d_1 = d_1 \circ q_2 = d_1 \circ k_2 \circ p_2, \end{aligned}$$

and since $p_1,p_2$ are epimorphisms, cancellation allows us to conclude that k is a functor (we note that $k_2$ is defined as $k_2(g,f) = (k_1g,k_1f)$, and hence $q_2 = k_2 \circ p_2$).

Again, pointwise calculation of pullbacks guarantees pullback stability. $\square$

Theorem 5.3

Let p be a functor of internal T-multicategories, and assume T preserves kernel pairs. If

• $p_1$ is an effective descent morphism in ${\mathcal {B}}$,

• $p_2$ is a descent morphism in ${\mathcal {B}}$,

• $p_3$ is an almost descent morphism in ${\mathcal {B}}$,

then p is effective for descent in ${{\textsf{Cat}} }(T,{\mathcal {B}})$.

Proof

By the previous lemma, and Proposition 2.1, the comparison functor ${\mathcal {K}}^p$ is fully faithful. Hence, we aim to prove that ${\mathcal {K}}^p$ is also essentially surjective under our hypotheses, thereby concluding that p is effective for descent.

Suppose we are given a $p^*p_!$-algebra $(a,\gamma )$, where $a :v \rightarrow x$ is a functor and $\gamma :u \rightarrow v$ is the algebra structure. We have equivalences ${\mathcal {K}}_i :{\mathcal {B}} \downarrow y_i \rightarrow {\textsf{Desc}}(p_i)$, for $i=0,\,1$, and $(a,\gamma )$ then determines algebras $(a_i,\gamma _i)$ for $i=0,1$. Hence, there exist $f_i :w_i \rightarrow y_i$ and $h_i :v_i \rightarrow w_i$ such that the following diagram

is a pullback square, and moreover, we have $h_i\circ \gamma _i = h_i \circ \epsilon _{p_i \circ a_i}$. We claim that

• $h_0, h_1$ determine a functor $h :v \rightarrow w$,

• $f_0, f_1$ determine a functor $f :w \rightarrow y$,

so that the above lifts to a pullback diagram of T-multicategories.

The hypothesis that $p_1, p_2$ are pullback-stable regular epimorphisms implies that $h_1, h_2$ are regular epimorphisms. Taking kernel pairs and noting that T preserves them, we get

therefore there exist unique morphisms making every right hand side square commute. We note that we define $h_2(g,f) = (h_1g, (Th_1)f)$. Assuming that w is in fact a T-multicategory, we may already conclude that h is a functor. The hypothesis that $p_1,p_2,p_3$ are pullback-stable epimorphisms implies that $h_1,h_2,h_3$ are epimorphisms. We have equations

$$\begin{aligned} d_1s_0h_0&= (Th_0)d_is_0 = (Th_0)e = eh_0 \\ d_0s_0h_0&= h_0d_0s_0 = h_0 \\ d_1d_1h_2&= (Th_0)d_1d_1 = (Th_0)m(Td_1)d_2 = m(Td_1)d_hk_2 \\ d_0d_1h_2&= h_0d_0d_1 = h_0d_0d_0 = d_0d_0h_2 \\ d_1s_ih_1&= h_1d_1s_i = h_1s_0d_0 = s_0d_0h_1 \\ d_1d_2h_3&= h_1d_1d_2 = h_1d_1d_1 = d_1d_1h_3 \end{aligned}$$

and by cancellation, we conclude w is a T-multicategory (proving our assumption) and, similarly, we can show that f is a functor, by following the same strategy as in the previous lemma. This confirms that $p^*$ is essentially surjective.

Finally, it is immediate that $h \circ \gamma = h \circ \epsilon _{p\circ a}$, since $h_i \circ \gamma _i = h_i \circ \epsilon _{p_i \circ a_i}$ for $i = 0,1$ and pullbacks are calculated pointwise. The result now follows by Corollary 2.3. $\square$

7 Epilogue

There are sparse examples of cartesian monads, and therefore sparse examples of categories of internal multicategories over a monad. For ${\mathcal {B}}$ finitely extensive with finite limits and pullback-stable nested countable unions, as in [16, Appendix D], the free category monad on graphs internal to ${\mathcal {B}}$ is cartesian, and therefore so is the free monoid monad ${{\,\mathrm{{\textsf{W}}}\,}}$ on ${\mathcal {B}}$. In fact, Leinster’s construction is iterable, and most known examples fit into the above conditions.

A class of examples outside of the previous setting is given by free monoid monads on extensive categories with finite limits (thus, trading off the requirement of the aforementioned unions by infinitary extensivity). These are also cartesian; the idea is that the coproduct functor ${\textsf{Fam}}({\mathcal {B}}) \rightarrow {\mathcal {B}}$ preserves finite limits, so we may construct the required limit diagrams in ${\textsf{Fam}}({\mathcal {B}})$, allowing us to conclude that such monads preserve pullbacks and that the required naturality squares are pullbacks.

Given a cartesian monad on a category ${\mathcal {B}}$ with pullbacks and ${\mathscr {C}}$ an internal T-multicategory, we can construct a cartesian monad $T_{{\mathscr {C}}}$ on ${\mathcal {B}} \downarrow {\mathscr {C}}_0$; see Corollary 6.2.5 ibid. This yields an equivalence of categories

$$\begin{aligned} {\textsf{Cat}}(T_{{\mathscr {C}}}, {\mathcal {B}} \downarrow {\mathscr {C}}_0) \cong {\textsf{Cat}}(T,{\mathcal {B}}) \downarrow {\mathscr {C}}, \end{aligned}$$

(10)

and since pullback-stable (regular) epimorphisms and effective descent remain unchanged on slice categories (more precisely, ${\mathcal {C}}/x \rightarrow {\mathcal {C}}$ creates each of the three types of morphism), we can deduce facts about effective descent of complicated internal multicategories in terms of simpler ones.

For the remainder of this section, we will discuss some simple examples of interest, compare our work with other literature, then mention some open problems.

$(M\times -)$-multicategories. Given a monoid M, we can define a cartesian monad $M \times -$ on ${\textsf{Set}}$. An $(M\times -)$-multicategory ${\mathscr {C}}$ is, intuitively, a category with weighted morphisms. $(M\times -)$-morphisms are of the form $f :x \xrightarrow {m} y$ for objects x, y and an element $m\in M$, and if $g :y \xrightarrow {n} z$, then $g \circ f :x \xrightarrow {n \cdot m} z$. Identities are given by ${\textsf {id}}:x \xrightarrow {1} x$, and these are to satisfy associativity and identity laws.

Despite being a more complicated structure than a category, $(M\times -)$-functors of effective descent are not harder to come by compared to ordinary functors. A well-known result (which can be deduced from (10)) is that ${\textsf{Cat}}(M\times -,{\textsf{Set}}) \cong {\textsf{Cat}}\downarrow M$, where we view M as a one object category. Hence, an $(M\times -)$-functor is an effective descent morphism whenever it has the respective property as a functor. In fact, since [15] characterizes effective descent functors, we have also characterized effective descent $(M\times -)$-functors. The arguments remain unchanged when we replace ${\textsf{Set}}$ by a lextensive category ${\mathcal {B}}$ (with regular epi-mono factorizations for the complete characterization).

Ordinary and operadic multicategories. A multicategory ${\mathscr {C}}$ consists of sets ${\mathscr {C}}_0$ and ${\mathscr {C}}_1$ of objects and multimorphisms, respectively, together with domain and codomain functions $d_1 :{\mathscr {C}}_1 \rightarrow {{\,\mathrm{{\textsf{W}}}\,}}{\mathscr {C}}_0$, $d_0 :{\mathscr {C}}_1 \rightarrow {\mathscr {C}}_0$, together with composition and unit operations $d_1 :\mathscr {C}_2 \rightarrow {\mathscr {C}}_1$ and $s_0 :{\mathscr {C}}_0 \rightarrow \mathscr {C}_1$ satisfying associativity and identity properties. Here, ${\mathscr {C}}_2$ is the set of multicomposable pairs given by the pullback of $d_1$ and $Td_0$. Likewise, ${\mathscr {C}}_n$ is the set of multicomposable n-tuples.

A multicategory functor $F :{\mathscr {C}} \rightarrow {\mathscr {D}}$ is given by a pair of functions on objects and multimorphisms which preserve domain, codomain, unit and composition. Our main result states that F is effective for descent whenever it is surjective on multimorphisms, multicomposable pairs, and multicomposable triples.

To extend this result using (10), suppose we have an operad $\mathcal O$ (a multicategory with one object). The induced monad ${{\,\mathrm{{\textsf{W}}}\,}}_{\mathcal O}$ is said to be an operadic monad, which is cartesian. These are related to strongly regular theories; we refer the reader to [16] and [4] for details. One could denote the category ${\textsf{Cat}}({{\,\mathrm{{\textsf{W}}}\,}}_{{\mathcal {O}}}, {\textsf{Set}})$ as the category of operadic multicategories and functors between them. These functors come with an underlying multicategory functor, and is effective for descent in ${\textsf{Cat}}({{\,\mathrm{{\textsf{W}}}\,}}_{\mathcal O},{\textsf{Set}})$ if and only if it is effective for descent in ${\textsf{Cat}}({{\,\mathrm{{\textsf{W}}}\,}},{\textsf{Set}})$. As in the previous case, the same arguments work for ${\mathcal {B}}$ lextensive.

State of the art. Our results have shown that three levels of “surjectivity” (of singles, pairs and triples of multimorphisms) are sufficient to determine effective descent in generalized multicategories. This is consistent with the findings of [12, 6.2 Proposition] for ${\textsf{Cat}}$, and in [15, Theorem 6.2.9] for ${\textsf{Cat}}({\mathcal {C}})$ where ${\mathcal {C}}$ has finite limits and a (regular epi, mono)-factorization, where these three levels are also necessary.

This is also the case for ${\mathcal {V}}$-categories, with ${\mathcal {V}}$ cartesian, as verified by [17, Theorem 9.11] (with suitable ${\mathcal {V}}$ lextensive), and [6, Theorem 5.4] (with ${\mathcal {V}}$ a complete Heyting lattice). In the latter case, since ${\mathcal {V}}$ is thin, surjectivity on triples of morphisms is no longer required.

In the enriched multicategory case, for T the ultrafilter monad and ${\mathcal {V}} = 2$ (so that $(T,{\mathcal {V}})\text {-}{\textsf{Cat}}= {\textsf{Top}}$), we have the result of [5, Theorem 5.2], which requires only two levels of surjectivity as well.

Further work. We also take the opportunity to state some open problems. One might be interested in verifying whether the converses to Theorems 4.5 or 5.3 hold. As mentioned in the introduction, LeCreurer gave an affirmative answer for $T={\textsf {id}}$ and further requiring a (regular epi, mono)-factorization on ${\mathcal {B}}$. One might also wonder if this extra condition is necessary.

Another interesting problem is to check whether LeCreurer’s tools are also amenable to fully characterize effective descent morphisms of enriched categories internal to ${\mathcal {B}}$.

Appendix A. T-stability of pullback-stable classes

The purpose of this appendix is to establish a couple of auxiliary lemmas about preservation of pullback-stable classes. Let $T = (T,e,m)$ be a cartesian monad on ${\mathcal {B}}$.

Lemma A.1

T creates any pullback-stable property of morphisms in its essential image.

Proof

If Tf satisfies a property P, stable under pullback, then the unit and multiplication naturality squares guarantee that f and TTf also satisfy P. $\square$

Corollary A.2

If Tf is a pullback-stable (regular) epimorphism, effective for descent, then f and TTf also have the respective property.

Lemma A.3

Let $f :x \rightarrow y$ be a T-graph morphism, and let ${\mathcal {E}}$ be a class of epimorphisms, containing all retractions, closed under composition and cancellation. If $f_1$ is in ${\mathcal {E}}$, then so is $f_0$.

Proof

Since $d_0 :y_1 \rightarrow y_0$ is a retraction, $d_0 \circ f_1 = f_0 \circ d_0$ is in ${\mathcal {E}}$, therefore so is $f_0$ by cancellation. $\square$

We are interested in the cases when ${\mathcal {E}}$ is the class of pullback-stable epimorphisms, of descent morphisms and of effective descent morphisms.