1 Introduction

COVID-19 is a contagious respiratory and vascular disease that has resulted in more than 498 million cases and 6 million deaths worldwide as of February 2022 (https://covid19.who.int/). It is caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) (https://www.who.int/health-topics/coronavirus#tab=tab_1).

Mathematical modeling of infectious diseases has become a highly researched area today. Mathematical epidemiology has contributed to a better understanding of the dynamic behavior of infectious diseases, their impact, and possible future predictions of their spread. Various compartmental models for understanding the dynamic behavior of COVID-19 can be found in Samui et al. (2020), Ndaïrou et al. (2020), Zeb et al. (2019), Leontitsis et al. (2021), Wang et al. (2020), Dashtbali and Mirzaie (2021), Zhao et al. (2020), Chen et al. (2020), Biswas et al. (2020), Sarkar et al. (2020), Chhetri et al. (2021). In Chhetri et al. (2021) a basic within-host model is developed to determine the crucial inflammatory mediators and the role of combined drug therapy in the treatment of COVID-19. A SAIU (Susceptible-Asymptomatic-Symptomatic Infectious-Unreported Symptomatic Infectious) compartmental mathematical model that explains the transmission dynamics of COVID-19 is developed in Samui et al. (2020). Some of the control policies, such as treatment, quarantine, isolation and screening, are also studied to control the spread of infectious diseases (Djidjou-Demasse et al. 2020; Libotte et al. 2020; Aronna et al. 2020). Some of the important mathematical modeling studies that deal with transmission and spread of COVID-19 at the population level can be found in Chen et al. (2020), Kucharski et al. (2020), Lin et al. (2019), Yang and Wang (2020). In the recent work (Hernandez-Vargas and Velasco-Hernandez 2020), an in-host modeling study deals with the qualitative characteristics and estimation of standard parameters of corona viral infections. In papers such as Kirschner and Webb (1997), Yang et al. (2020), within-host mathematical models have been used to simulate combination chemotherapy with reverse transcriptase inhibitors and protease inhibitors in HIV infection. These studies have shown that survival is proportional to the amount of CD4+ cells. Today, the combination of these interventions is the mainstay of treatment for HIV infection, and survival outcomes depend on CD4+ cell counts.

A detailed within-host study involving crucial inflammatory mediators and the host immune response has been developed and discussed at length by the authors in Chhetri et al. (2021). The work in Chhetri et al. (2021) dealt with the natural history and course of infection of COVID-19. The authors also briefly discussed about the optimality and effectiveness of combined therapy involving one or more antiviral and one or more immuno-modulating drugs when administered together.

The present work is an extension of the previous work (Chhetri et al. 2021), and deals with optimal drug regimen and the efficacy of combined therapy in treatment of the COVID-19. The drug interventions considered include Arbidol, Remdesivir, Interferon and Lopinavir/Ritonavir. Four scenarios involving administration of a single drug, two drugs, three drugs and all four drugs have been discussed. In all these scenarios the optimal drug regimen is proposed based on two methods. The first method is the optimal control problem setting, and the second method is a comparative effectiveness study.

2 Initial Model

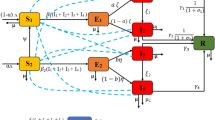
The following within-host model is developed based on the pathogenesis of the COVID-19 disease. The details about the formulation of the model are discussed in Chhetri et al. (2021) (Tables 1 and 2).

$$\begin{aligned} \frac{dS}{dt} &= {} \omega \ - \beta SV - \mu S , \end{aligned}$$
(2.1)
$$\begin{aligned} \frac{dI}{dt} &= {} \beta SV \ - { \bigg (d_{1} + d_{2} + d_{3} + d_{4} + d_{5}+ d_{6}\bigg )I } \ - \mu I , \end{aligned}$$
(2.2)
$$\begin{aligned} \frac{dV}{dt} &= {} \alpha I \ - \bigg ( b_{1} + b_{2} + b_{3} + b_{4}+ b_{5} + b_{6}\bigg )V \ - \mu _{1} V. \end{aligned}$$
(2.3)
Table 1 Variables/Parameters and their biological meaning
Full size table

2.1 Well-Posedness of the Model

The existence, positivity and the boundedness of the solutions of the proposed model \((2.1){\text{--}}(2.3)\) need to be proved to ensure that the model has a mathematical and biological meaning.

The positivity and boundedness of the solution of the system \((2.1){\text{--}}(2.3)\) is discussed by the authors in details in Chhetri et al. (2021).

The biologically feasible region of the system \((2.1){\text{--}}(2.3)\) as discussed in Chhetri et al. (2021) is defined by the set \(\Omega\),

$$\begin{aligned} \Omega = \bigg \{\bigg (S(t), I(t), V(t)\bigg ) \in {\mathbb {R}}^{3}_{+} : S(t) + I(t) + V(t) \le \frac{\omega }{\mu }, \ t \ge 0 \bigg \}. \end{aligned}$$

2.1.1 Existence and Uniqueness of Solution

In similar lines to Sowole et al. (2019), in this section we discuss the existence and uniqueness of a solution of the system \((2.1){\text{--}}(2.3)\).

For the general first order ODE of the form

$$\begin{aligned} \dot{x}=f(t,x), \quad x(t_0)=x_0, \end{aligned}$$
(2.4)

with f : R x \(R^{n} \rightarrow R^n\) sufficiently many times differentiable, one would have interest in knowing the answers to the following questions:

  1. (i)

    Under which conditions does a solution exist for (2.4)?

  2. (ii)

    Under which conditions does a unique solution exist for (2.4)?

We use the following theorem discussed in Sowole et al. (2019) to establish the existence and uniqueness of a solution for our SIV model \((2.1){\text{--}}(2.3)\).

Theorem 2.1

Let D denote the domain:

$$\begin{aligned} |t-t_0| \le a, ||x-x_0|| \le b, x=(x_1, x_2,..., x_n), x_0=(x_{10},..,x_{n0}), \end{aligned}$$

and suppose that f(t, x) satisfies the Lipschitz condition:

$$\begin{aligned} ||f(t,x_2)-f(t, x_1)|| \le k ||x_2-x_1|| \end{aligned}$$
(2.5)

whenever the pairs \((t,x_1)\) and \((t, x_2)\) belong to the domain D, where k is a positive constant. Then, there exists a constant \(\delta > 0\) such that a unique (exactly one) continuous vector solution x(t) exists for the system (2.4) in the interval \(|t-t_0|\le \delta\).

It is important to note that condition (2.5) is satisfied by the requirement that:

$$\begin{aligned} \frac{\partial f_i}{\partial x_j}, i,j=1,2,.., n, \end{aligned}$$

be continuous and bounded in the domain D.

Theorem 2.2

Existence of Solution Let D be the domain defined above such that (2.5) holds. Then, there exists a unique solution of the system (2.1)–(2.3), which is bounded in the domain D.

Proof

Let

$$\begin{aligned} f_1 &= {} \omega \ - \beta S(t)V(t) - \mu S(t) , \end{aligned}$$
(2.6)
$$\begin{aligned} f_2 &= {} \beta S(t)V(t) \ - (p+\mu )I(t) , \end{aligned}$$
(2.7)
$$\begin{aligned} f_3 &= {} \alpha I(t)-(q+\mu _1)V(t), \end{aligned}$$
(2.8)

where

$$\begin{aligned} p =d_{1}+d_{2}+d_{3}+d_{4}+d_{5}+d_{6}, \\ q=b_{1}+b_{2}+b_{3}+b_{4}+b_{5}+b_{6}. \end{aligned}$$

We will show that

$$\begin{aligned} \frac{\partial f_i}{\partial x_j}, i,j=1,2,.., n, \end{aligned}$$

is continuous and bounded in the domain D.

From Eq. (2.6) we have

$$\begin{aligned} \frac{\partial f_1}{\partial S} &= {} -\beta V-\mu , \bigg |\frac{\partial f_1}{\partial S}\bigg |=|-\beta V -\mu |< \infty ,\\ \frac{\partial f_1}{\partial I} &= {} 0, \bigg |\frac{\partial f_1}{\partial I}\bigg |< \infty ,\\ \frac{\partial f_1}{\partial V} &= {} -\beta S, \bigg |\frac{\partial f_1}{\partial V}\bigg |=|-\beta S| < \infty . \end{aligned}$$

Similarly, from Eq. (2.7) we have

$$\begin{aligned} \frac{\partial f_2}{\partial S} &= {} \beta V, \bigg |\frac{\partial f_2}{\partial S}\bigg |=|\beta V|< \infty ,\\ \frac{\partial f_2}{\partial I}= & {} -\mu -p, \bigg |\frac{\partial f_2}{\partial I}\bigg | = |-(\mu +p)|< \infty ,\\ \frac{\partial f_2}{\partial V}= & {} \beta S, \bigg |\frac{\partial f_2}{\partial V}\bigg |=|\beta S| < \infty . \end{aligned}$$

Finally, from (2.8) we have

$$\begin{aligned} \frac{\partial f_3}{\partial S} &= {} 0, \bigg |\frac{\partial f_3}{\partial S}\bigg |< \infty ,\\ \frac{\partial f_3}{\partial I} &= {} \alpha , \bigg |\frac{\partial f_3}{\partial I}\bigg | = |\alpha |< \infty ,\\ \frac{\partial f_3}{\partial V} &= {} -(\mu _1 + q), \bigg |\frac{\partial f_3}{\partial V}\bigg |=|-(\mu _1 + q)| < \infty . \end{aligned}$$

Hence we have shown that all the partial derivatives are continuous and bounded. Therefore, Lipschitz condition (2.5) is satisfied. Hence, by Theorem 2.1 there exists a unique solution of system (2.1)–(2.3) in the region D. \(\square\)

The existence of equilibrium points of the system (2.1)–(2.3) and their stability is discussed in details in Chhetri et al. (2021). The system is shown to undergo a forward (transcritical) bifurcation at \(R_0=1\).

The following are the major objectives of the present study.


Objectives of the study

  1. 1.

    To investigate the role of pharmaceutical interventions such as Arbidol, Remdesivir, Interferon and Lopinavir/Ritonavir by incorporating them as controls at specific compartments in the model \((2.1){\text{--}}(2.3)\) depending on their functionality.

  2. 2.

    To study and compare the dynamics of susceptible and infected cells and the viral load with and without these control interventions, by studying them as optimal control problems.

  3. 3.

    To propose the optimal drug regimen in four scenarios involving administration of a single drug, two drugs, three drugs and all four drugs based on the average susceptible and infected cell counts, the average viral load, and the basic reproduction number.

  4. 4.

    To propose the optimal drug regimen using a comparative effectiveness study.

3 Optimal Control Studies

3.1 Optimal Control Problem Formulation

Drugs such as Remdesivir inhibit RNA-dependent RNA polymerase, and drugs Lopinavir/Ritonavir inhibit the viral protease by reducing viral replication (Tu et al. 2020). Interferons are broad spectrum antivirals, exhibiting both direct inhibitory effect on viral replication and supporting an immune response to clear virus infection (Wang and Fish 2019). On the other hand drugs such as Arbidol not only inhibit the viral replication but also block the virus replication by inhibiting the fusion of lipid membranes with host cells (Yang et al. 2020).

Motivated by the above clinical findings in similar lines to the control problem in Chhetri et al. (2021), we consider a control problem with the drug interventions Arbidol, Remdesivir, Lopinavir/Ritonavir and Interferon as controls. The dynamic model based on the pathogenesis described above with control variables is described by the following system of nonlinear differential equations:

$$\begin{aligned} \frac{dS}{dt} &= {} \omega \ - \beta SV -\mu _{1A}(t)S -\mu S , \end{aligned}$$
(3.1)
$$\begin{aligned} \frac{dI}{dt} &= {} \beta SV \ - { \bigg (d_{1} + d_{2} + d_3 + d_{4} + d_{5}+ d_{6}\bigg )I} \nonumber \\&-\bigg (\mu _{2Rem}(t)+\mu _{2INF}(t)+\mu _{2A}(t)+\mu _{2Lop/Rit}(t)\bigg )I-\mu I, \end{aligned}$$
(3.2)
$$\begin{aligned} \frac{dV}{dt} &= {} \bigg ( \alpha -(\mu _{3Rem}(t)+\mu _{3INF}(t)+\mu _{3A}(t)+\mu _{3Lop/Rit}(t))\bigg ) I, \nonumber \\&- \bigg ( b_{1} + b_{2} + b_3 + b_{4}+ b_{5} + b_{6}\bigg )V \mu _{1} V . \end{aligned}$$
(3.3)
Table 2 Biological meaning of control variables
Full size table

For simplicity, we define \(U_1, U_2, U_3\) and \(U_4\) as follows,

$$\begin{aligned} U_1 &= {} (\mu _{1A}, \mu _{2A}, \ \mu _{3A}), \ U_2 = (\mu _{2Rem}, \mu _{3Rem}), \\ U_3 &= {} (\mu _{2INF}, \mu _{3INF}), \ U_4 = (\mu _{2Lop/Rit}, \mu _{3Lop/Rit}). \end{aligned}$$

With this notation, the set of all admissible controls is given by

$$\begin{aligned} \begin{aligned} U&= \{(U_1(t), U_2(t), U_3(t), U_4(t)) : U_1(t) \in [0,U_{1} max],\\&\quad U_{2}(t) \in [0,U_{2} max], U_3(t) \in [0,U_{3} max], \\&\quad U_{4}(t) \in [0,U_{4} max], t \in [0,T] \}. \end{aligned} \end{aligned}$$

Here, all the control variables are measurable and bounded functions, and T is the final time of the applied control interventions. The upper bounds of control variables are based on the resource limitation and the limit to which these drugs would be prescribed to the patients. Our main objective of this study is to investigate such optimal control functions that maximizes the benefits of each of the drug interventions and minimize the cumulative count of infected cells and viral load.

Based on the above, we consider the following objective function that we wish to maximize.

$$\begin{aligned} \begin{aligned} J(U_1, U_2, U_3, U_4 )&= \int _{0}^{T} \bigg [A_1 \bigg (\mu _{1A}^2(t)+\mu _{2A}^2(t)+\mu _{3A}^2(t)\bigg ) + A_2 \bigg (\mu _{2Rem}^2(t)+\mu _{3Rem}^2(t)\bigg )\\&\quad + A_3 \bigg (\mu _{2INF}^2(t)+\mu _{3INF}^2(t)\bigg ) \\&\quad + A_4\bigg (\mu _{2Lop/Rit}^2(t)+\mu _{3Lop/Rit}^2(t)\bigg ) -I(t) - V(t) \bigg ] dt. \end{aligned} \end{aligned}$$
(3.4)

subject to the system

$$\begin{aligned} \frac{dS}{dt} &= {} \omega \ - \beta SV -\mu _{1A}(t)S -\mu S , \end{aligned}$$
(3.5)
$$\begin{aligned} \frac{dI}{dt} &= {} \beta SV \ - { \bigg (d_{1} + d_{2} + d_3 + d_{4} + d_{5}+ d_{6}\bigg )I} \nonumber \\& \quad -\bigg (\mu _{2Rem}(t)+\mu _{2INF}(t)+\mu _{2A}(t)+\mu _{2Lop/Rit}(t)\bigg )I-\mu I, \end{aligned}$$
(3.6)
$$\begin{aligned} \frac{dV}{dt} &= {} \bigg ( \alpha -(\mu _{3Rem}(t)+\mu _{3INF}(t)+\mu _{3A}(t)+\mu _{3Lop/Rit}(t))\bigg ) I \nonumber \\& \quad - \bigg ( b_{1} + b_{2}+b_3 + b_{4}+ b_{5} + b_{6}\bigg )V \mu _{1} V. \end{aligned}$$
(3.7)

with initial conditions \(S(0)>0\), \(I(0) \ge 0\) and \(V(0)\ge 0\).

The antiviral drugs and immunomodulators when administered can have multiple effects, this justifies the quadratic terms in the definition of the objective function (Joshi 2002). Also, when the objective function is defined as a linear combination of the quadratic terms of control variables the complexity of the problem reduces. Some of the studies in which an objective function is considered as a linear combination of the quadratic terms of control variables can be found in Madubueze et al. (2020), Kamyad et al. (2014). Higher orders of control variables in objective functions sometimes may lead to complications (Lee et al. 2010; Khatua et al. 2020).

The integrand of the cost functional (3.4), given by

$$\begin{aligned} \begin{aligned} L(U_1, U_2, U_3, U_4,I, V )&= A_1 \bigg (\mu _{1A}^2(t)+\mu _{2A}^2(t)+\mu _{3A}^2(t)\bigg ) \\&\quad + A_2 \bigg (\mu _{2Rem}^2(t)+\mu _{3Rem}^2(t)\bigg ) \\&\quad + A_3 \bigg (\mu _{2INF}^2(t)+\mu _{3INF}^2(t)\bigg )\\&\quad + A_4\bigg (\mu _{2Lop/Rit}^2(t)+\mu _{3Lop/Rit}^2(t)\bigg ) -I(t) - V(t) \end{aligned} \end{aligned}$$

is called the Lagrangian of the running cost.

Here the cost functional (3.4) represents the benefits of each of the interventions and the number of infected cells and viral load throughout the observation period. Our goal is to maximize the benefits of each of the interventions and minimize the infected cell and virus population. The coefficients \(A_{i}\), for \(i = 1, 2, 3, 4,\) are the positive weight constants related to the benefits of each of the drug interventions.

The admissible solution set for the optimal control problem \((3.4){\text{--}}(3.7)\) is given by

$$\begin{aligned} \Omega = \left\{ (S, I, V, U_1, U_2, U_3, U_4)\; | \; S, I \ and \ V \text { satisfy} \ (3.5)-(3.7), \ \forall \ U_i \in U \right\} . \end{aligned}$$

All the control variables considered here are measurable and bounded functions. The upper limits of the control variables depends on the resource constraint.

4 Existence of Optimal Controls

Before trying to find an optimal control solutions, the first fundamental question is to know whether an optimal solution even exists. An existence theorem certifies that the problem has a solution before attempting to compute an optimal control. In order to prove the existence of optimal control functions that maximize the objective function within a finite time span [0, T], we will show that the conditions stated in Theorem 4.1 of Fleming and Rishel (2012) is satisfied.

Theorem 4.1

There exists a 9-tuple of optimal controls

$$\begin{aligned}&\bigg (\mu _{1A}^{*}(t), \mu _{2A}^{*}(t), \mu _{3A}^{*}(t), \mu _{2Rem}^{*}(t), \mu _{3Rem}^{*}(t), \mu _{2INF}^{*}(t), \mu _{3INF}^{*}(t),\\&\quad \mu _{2Lop/Rit}^{*}(t), \mu _{3Lop/Rit}^{*}(t)\bigg ) \end{aligned}$$

in the set of admissible controls U such that the cost functional \(J(U_1,U_2,U_3,U_4)\) is maximized corresponding to the optimal control problem \((3.4){\text{--}}(3.7)\).

Proof

In order to show the existence of optimal control functions, we will show that the following conditions are satisfied :

  1. 1.

    The solution set for the system \((3.5){\text{--}}(3.7)\) along with bounded controls must be non-empty, i.e., \(\Omega \ne \phi\).

  2. 2.

    Control set U is closed and convex, and the system should be expressed linearly in terms of the control variables with coefficients that are functions of time and state variables.

  3. 3.

    The integrand of the objective function is concave on U.

  4. 4.

    There exists constants \(c_1>0, c_2>0, c_3 >0\) and \(s>1\) such that the integrand of the objective functional satisfies

    $$\begin{aligned} \begin{aligned} L(U_1, U_2, U_3, U_4,I, V )&\le c_1\bigg [ \bigg (\mu _{1A}^2(t)+\mu _{2A}^2(t)+\mu _{3A}^2(t)\bigg ) + \bigg (\mu _{2Rem}^2(t)+\mu _{3Rem}^2(t)\bigg ) \\&+ \bigg (\mu _{2INF}^2(t)+\mu _{3INF}^2(t)\bigg ) + \bigg (\mu _{2Lop/Rit}^2(t)+\mu _{3Lop/Rit}^2(t)\bigg ) \bigg ]^{\frac{s}{2}}\\&-c_2-c_3. \end{aligned} \end{aligned}$$

Now we will show that each of the conditions are satisfied:

  1. 1.

    From the positivity and boundedness of the solutions of the system \((3.5){\text{--}}(3.7)\) established in Chhetri et al. (2021), all solutions remain positive and bounded for each control variable in U. Also, the right hand side of the system \((3.5){\text{--}}(3.7)\) satisfies a Lipschitz condition with respect to state variables. Hence, using the positivity and boundedness condition and the existence of a solution from the Picard-Lindelof Theorem (Makarov and Spitters 2013), we have satisfied condition 1.

  2. 2.

    U is closed and convex by definition. Also, the system \((3.5){\text{--}}(3.7)\) is clearly linear with respect to the controls, such that the coefficients are only state variables or functions dependent on time. Hence condition 2 is satisfied.

  3. 3.

    We know that a differentiable function is concave if and only if its derivative is non-increasing (decreasing). From the definition, we see that \(L(U_1, U_2, U_3, U_4,I, V )\) has a non-increasing slope. Therefore, L is concave on U.

  4. 4.

    From the definition of the Lagrangian we see that,

$$\begin{aligned} \begin{aligned} L(U_1, U_2, U_3, U_4,I, V )&\le c_1\bigg [ \bigg (\mu _{1A}^2(t)+\mu _{2A}^2(t)+\mu _{3A}^2(t)\bigg ) \\&\quad + \bigg (\mu _{2Rem}^2(t)+\mu _{3Rem}^2(t)\bigg ) \\&\quad + \bigg (\mu _{2INF}^2(t)+\mu _{3INF}^2(t)\bigg ) \\&\quad + \bigg (\mu _{2Lop/Rit}^2(t)+\mu _{3Lop/Rit}^2(t)\bigg ) \bigg ]\\&\quad -c_2-c_3, \end{aligned} \end{aligned}$$

where \(c_1=\max \{A_1,A_2,A_3,A_4\}\) and \(c_2\) and \(c_3\) are lower bounds on I(t) and V(t).

Hence there exist optimal controls that maximize the cost functional (3.4).

The proof of the existence theorem done here is in similar lines to the proof done in Joshi (2002). \(\square\)

5 Characteriztion of Optimal Controls

We now obtain the necessary conditions for optimal control functions using the Pontryagin’s Maximum Principle (Liberzon 2011), and also obtain the characteristics of the optimal controls.

The Hamiltonian for this problem is given by

$$\begin{aligned}&H(S, I , V, \mu _{1A}, \mu _{2A}, \mu _{3A}, \mu _{2Rem}, \mu _{3Rem}, \mu _{2INF}, \mu _{3INF}, \mu _{2Lop/Rit}, \mu _{3Lop/Rit},\lambda ) \\&= L( I, V, \mu _{1A}, \mu _{2A}, \mu _{3A}, \mu _{2Rem}, \mu _{3Rem}, \mu _{2INF}, \mu _{3INF}, \mu _{2Lop/Rit}, \mu _{3Lop/Rit}) \\&+ \lambda _{1} \frac{\mathrm {d} S}{\mathrm {d} t} \\&+\lambda _{2}\frac{\mathrm {d} I}{\mathrm {d} t}+ \lambda _{3} \frac{\mathrm {d} V}{\mathrm {d} t}. \end{aligned}$$

here \(\lambda\) = (\(\lambda _{1}\),\(\lambda _{2}\),\(\lambda _{3}\)) is called the co-state vector or the adjoint vector and \(\lambda _{1} (T) = 0, \ \lambda _{2} (T) = 0, \ \lambda _{3} (T) = 0.\)

Now the canonical equations that relate the state variables to the co-state variables are given by

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d} \lambda _{1}}{\mathrm {d} t}&= -\frac{\partial H}{\partial S},\\ \frac{\mathrm {d} \lambda _{2}}{\mathrm {d} t}&= -\frac{\partial H}{\partial I},\\ \frac{\mathrm {d} \lambda _{3}}{\mathrm {d} t}&= -\frac{\partial H}{\partial V}. \end{aligned} \end{aligned}$$
(5.1)

Substituting the Hamiltonian value gives the canonical system

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d} \lambda _{1}}{\mathrm {d} t}&= \lambda _{1}(\beta V+\mu +\mu _{1A})-\lambda _{2} \beta V,\\ \frac{\mathrm {d} \lambda _{2}}{\mathrm {d} t}&= 1+\lambda _{2}\bigg (x+(\mu _{2A}+\mu _{2Rem}+\mu _{2INF}+\mu _{2Lop/Rit}+\mu )\bigg )\\ {}&- \lambda _{3} \bigg (\alpha -(\mu _{3A}+\mu _{3Rem}+\mu _{3INF}+\mu _{3Lop/Rit})\bigg ),\\ \frac{\mathrm {d} \lambda _{3}}{\mathrm {d} t}&= 1+\lambda _{1}\beta S-\lambda _{2}\beta S+\lambda _{3}(y+\mu _{1}). \end{aligned} \end{aligned}$$
(5.2)

where \(x=d_{1}+d_{2}+d_3 + d_{4}+d_{5}+d_{6}\) and \(y=b_{1}+b_{2}+b_3 + b_{4}+b_{5}+b_{6}\), along with the transversality conditions \(\lambda _1(T) = 0, \lambda _2(T) = 0, \lambda _3(T) = 0\). Now, to obtain the optimal controls, we use the Hamiltonian minimization condition \(\frac{\partial H}{\partial u} = 0\), for each \(u \in U\) at \(u^{*}.\)

Differentiating the Hamiltonian and solving the equations, we obtain the optimal controls as

$$\begin{aligned} \mu _{1A}^{*}= & {} \min \bigg \{ \max \bigg \{\frac{\lambda _{1}S}{2A_{1}},0 \bigg \}, \mu _{1A}max\bigg \},\\ \mu _{2A}^{*}= & {} \min \bigg \{ \max \bigg \{\frac{\lambda _{2}I}{2A_{1}},0 \bigg \}, \mu _{2A}max\bigg \},\\ \mu _{3A}^{*}= & {} \min \bigg \{ \max \bigg \{\frac{\lambda _{3}I}{2A_{1}},0 \bigg \}, \mu _{3A}max\bigg \},\\ \mu _{2Rem}^{*}= & {} \min \bigg \{ \max \bigg \{\frac{\lambda _{2}I}{2A_{2}},0 \bigg \}, \mu _{2Rem}max\bigg \},\\ \mu _{3Rem}^{*}= & {} \min \bigg \{ \max \bigg \{\frac{\lambda _{3}I}{2A_{2}},0 \bigg \}, \mu _{3Rem}max\bigg \},\\ \mu _{2INF}^{*}= & {} \min \bigg \{ \max \bigg \{\frac{\lambda _{2}I}{2A_{3}},0 \bigg \}, \mu _{2INF}max\bigg \},\\ \mu _{3INF}^{*}= & {} \min \bigg \{ \max \bigg \{\frac{\lambda _{3}I}{2A_{3}},0 \bigg \}, \mu _{3INF}max\bigg \},\\ \mu _{2Lop/Rit}^{*}= & {} \min \bigg \{ \max \bigg \{\frac{\lambda _{2}I}{2A_{4}},0 \bigg \}, \mu _{2Lop/Rit}max\bigg \},\\ \mu _{3Lop/Rit}^{*}= & {} \min \bigg \{ \max \bigg \{\frac{\lambda _{3}I}{2A_{4}},0 \bigg \}, \mu _{3Lop/Rit}max\bigg \}. \end{aligned}$$

6 Optimal Drug Regimen

In this section we perform numerical simulations to understand the efficacy of single and multiple drug interventions and propose the optimal drug regimen in these scenarios. This is done by studying the effect of the corresponding controls on the dynamics of the system \((3.5){\text{--}}(3.7).\)

The efficacy of various combinations of controls considered are:

  1. 1.

    Single drug/intervention administration.

  2. 2.

    Two drugs/interventions administration.

  3. 3.

    Three drugs/interventions administration.

  4. 4.

    All the four drugs/interventions administration.

For our simulations, we have taken the total number of days as \(T =30\). All the parameter values used for simulation are taken from Chhetri et al. (2021) and are listed below. Some of these parameter values are estimated minimizing the root mean square difference between the model predictive output and the experimental data and some are taken from the existing literature. The details and the motivation for the same can be found in Chhetri et al. (2021).

We first solve the state system numerically using the fourth order Runge-Kutta method in MATLAB. We take the initial values of state variables to be \(S(0) = 3.5 \times 10^5, I(0) = 0, V(0) = 5\), and the initial values of the control parameters as zeros. Since the incubation period of SARS-COV-2 is approximately 4-5 days (Chhetri et al. 2021), initially we allow the system to grow for 5 days without considering any controls. The population of susceptible cells, infected cells and viral load after 5 days were calculated to be \(3.4971 \times 10^5, 176, 25\) respectively. Considering these as initial values we simulate the system with controls and explore the roles of individual drugs and combination therapy in reducing the infected cells and viral load.

To simulate the system with controls, we use the method Forward-Backward Sweep, starting with the initial values of the controls at zero and solving the state system forward in time. We then solve the adjoint state system backwards in time due to the transversality constraints, using the optimal state variables and the initial values of the optimal controls, which are zero.

The values of the adjoint state variables are now used to update the values of the optimal controls, and this process is run again with these updated control variables. We continue this process until the convergence criterion is satisfied (Liberzon 2011).

In survival analysis, the hazard ratio (HR) plays a crucial role in determining the rate at which the people treated by drugs may suffer a certain complication per unit time as compared to a population treated without drugs. The larger the hazard ratio, the more harmful the drugs to be administered. We use this concept in assigning weights to our objective function in our model. In the following Table 3 we enlist the the hazard ratios for the four drugs considered in this work.

Table 3 Hazard Ratios (HR) for drugs considered
Full size table

From Table 3 we see that the hazard ratio of Remdesivir is 44.5 percent more than that of Arbidol, therefore we take the value of the weight constant associated with Remdesivir (A2) to be 44.5 percent less than that of Arbidol. The hazard ratio of INF is 12 percent more than that of Remdesivir, therefore the value of weight associated with INF(A3) will be chosen 12 percent less than that of Remdesivir. Similarly the value of weight constant A4 will be obtained.

Based on the above we choose \(A_{1}\) = 500, \(A_{2}\) = 277.5, \(A_{3}\) = 244.2, \(A_{4}\) = 228.9375, where the value of \(A_1\) was fixed at 500 as baseline. Since our objective is to maximize the benefits of each of the interventions and to minimize the infected cell and virus population, we have taken a higher value of the coefficient associated with the drug intervention with least hazard ratio. \(A_{1}\) is chosen high compared to the other coefficients because it has the least hazard ratio.

6.1 Without Any Drugs/Interventions

In this section we simulate the behavior of susceptible and infected cells and viral load in the absence of drug intervention over a time period of 30 days. As can be seen from Fig. 1 the susceptible cells reduce and the infected cells increase exponentially due to the increase in viral load over a period of time.

Fig. 1
figure 1

Figure depicting the S(t), I(t), V(t) populations without control interventions over time. The exponential growth of the infected cells and viral load can be observed

Full size image

6.2 Single Drug/Intervention

In this section we study the dynamics of susceptible and infected cells and viral load when each of the four drugs is administered individually. Figures 2, 3 and 4 depict the susceptible and infected population and viral load. We recall here that the symbols \(U_1, U_2, U_3\), and \(U_4\) denote the administration of drugs Arbidol, Remdesivir, Inteferon, and Lopinavir/Ritonavir respectively.

Table 4 Table depicting the average values of the susceptible cells, infected cells and the viral load with respect to each of the drug interventions administered individually at a time
Full size table
Fig. 2
figure 2

Figure depicting S(t) under each of the single optimal controls \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image
Fig. 3
figure 3

Figure depicting I(t) under each of the single optimal controls \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image
Fig. 4
figure 4

Figure depicting V(t) under each of the single optimal controls \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image

In Table 4 the average values of the susceptible cells and infected cells and the viral load with respect to each of these drug interventions when administered individually are listed. Here the average is taken over the time period of 30 days. From this Table 4 it can be seen that the drug Lopinavir/Ritonavir (\(U_4 = U_4^*\)) reduces the infected cells and viral load the best compared to other drugs when administered individually, followed by drug INF (\(U_3 = U_3^*\)). On the other hand drug Arbidol (\(U_1 = U_1^*\)) does the best job in reducing the susceptible cells.

6.3 Two Drugs/Interventions

In this section we study the dynamics of susceptible and infected cells and the viral load when two control interventions are administered at a time. Figures 5, 6 and 7 depict the susceptible, infected population and viral load.

Table 5 Table depicting the average values of the susceptible cells and infected cells and the viral load with respect to two control interventions administered at a time
Full size table

In Table 5 the average values of the susceptible cells and infected cells and the viral load with respect to two control interventions administered at a time are listed. From this Table 5 it can be seen that the combination of INF and Lopinavir/Ritonavir (\(U_3 = U_3^*, U_4 = U_4^*\)) reduces the infected cells and viral load the best compared to other combinations of two drugs when administered, followed by drug combination Remdesivir and INF (\(U_2 = U_2^*, U_3 = U_3^*\)). On the other hand, the drug combination of Arbidol and Remdesivir \((U_1 = {{U_1}^*}, U_2 = {U_2}^*)\) does the best job in reducing the susceptible cells.

Fig. 5
figure 5

Figure depicting S(t) under each combination of two different controls taken from \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image
Fig. 6
figure 6

Figure depicting I(t) under each combination of two different controls taken from \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image
Fig. 7
figure 7

Figure depicting V(t) under each combination of two different controls taken from \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image

6.4 Three Drugs/Interventions

In this section we study the dynamics of susceptible and infected cells and viral load when three control interventions are administered at a time. Figures 8, 9 and 10 depict the susceptible and infected population and viral load.

Table 6 Table depicting the average values of the susceptible cells and infected cells and the viral load with respect to three control interventions administered at a time
Full size table

In Table 6 the average values of the susceptible cells and infected cells and the viral load with respect to three control interventions administered at a time are listed. From this Table 6 it can be seen that the combination of Arbidol, INF and Lopinavir/Ritonavir (\(U_1 = U_1^*, U_3 = U_3^*, U_4 = U_4^*\)) reduces the infected cells and viral load the best compared to other combinations of drugs when administered, followed by drug combination Arbidol, Remdesivir and Lopinavir/Ritonavir (\(U_1 = U_1^*, U_2 = U_2^*, U_4 = U_4^*\)). On the other hand, surprisingly the average number of the susceptible cells are less in the no control intervention case compared to any other case having three control interventions.

Fig. 8
figure 8

Figure depicting S(t) under each combination of three different controls taken from \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image
Fig. 9
figure 9

Figure depicting I(t) under each combination of three different controls taken from \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image
Fig. 10
figure 10

Figure depicting V(t) under each combination of three different controls taken from \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image

6.5 Four Drugs/Interventions

In this section we study the dynamics of susceptible and infected cells and viral load when all the four control interventions are administered at a time. Figures 11, 12, 13 and 14 depict the susceptible and infected population and viral load.

Table 7 Table depicting the average values of the susceptible cells and infected cells and the viral load with respect to four control interventions administered at a time
Full size table

In Table 7 the average values of the susceptible cells and infected cells and the viral load with respect to all four control interventions administered at a time are listed. From this Table 7 it can be seen that the combination of all four drug interventions reduces the infected cells and viral load compared to the no intervention case. As in the three drug control intervention case here also the average number of the susceptible cells are less in the no control case compared to all the four control case. Comparing the infected cells and viral load for all the possible combinations of controls as described we observe that implementation of all the four drugs together at a time gives the best result in terms of minimizing the infection and the viral load.

Fig. 11
figure 11

Figure depicting S(t) under combination of all four controls \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image
Fig. 12
figure 12

Figure depicting I(t) under combination of all four controls \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image
Fig. 13
figure 13

Figure depicting V(t) under combination of all four controls \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image

In Fig. 14 we increase the time period to 100 days and plot the infected cell population and viral load under combination of all four controls \(U_1^*, U_2^*, U_3^*, U_4^*\). With all four controls together we see that the infected cell count and the viral load is less compared to the different combinations discussed above for the entire time period considered. The infected cell population is found to increase for the initial period and is found to remain almost constant after 30 days whereas the viral load is found to decrease and remain at very low level after a certain period of time causing no new infections and thereby producing no new infected cells. This proves that combined drug therapy can be effective in keeping the viral load low.

Fig. 14
figure 14

Figure depicting I(t) and V(t) under combination of all four controls \(U_1^*, U_2^*, U_3^*, U_4^*\)

Full size image

7 Comparative Effectiveness Study

In this section we perform the comparative effectiveness study for the system

$$\begin{aligned} \frac{dS}{dt} &= {} \omega \ - \beta SV -\mu S , \end{aligned}$$
(7.1)
$$\begin{aligned} \frac{dI}{dt} &= {} \beta SV \ - { \bigg (d_{1} + d_{2} +d_3 + d_{4} + d_{5}+ d_{6}\bigg )I} -\mu I , \end{aligned}$$
(7.2)
$$\begin{aligned} \frac{dV}{dt} &= {} \alpha I -\bigg ( b_{1} + b_{2}+ b_3 + b_{4}+ b_{5} + b_{6}\bigg )V \ - \mu _{1} V. \end{aligned}$$
(7.3)

The basic reproductive number for the system (7.1)–(7.3) as obtained in Kirschner and Webb (1997) is given by

$$\begin{aligned} {\mathcal {R}}_{0} = \frac{ \beta \alpha \omega }{\mu (b_{1}+b_{2}+ b_3+b_{4}+b_{5}+b_{6}+\mu _1)(d_{1}+d_{2}+ d_3 + d_{4}+d_{5}+d_{6}+\mu )}. \end{aligned}$$
(7.4)

The disease-free equilibrium for the system can be seen to be

$$\begin{aligned} E^{0} = \left( S^{0} , I^{0} , V^{0} \right) = \left( \frac{\omega }{\mu }, 0, 0 \right) , \end{aligned}$$
(7.5)

and the endemic equilibrium to be

$$\begin{aligned} {\overline{S}}&= \frac{\left( b_{1}+b_{2}+b_3+b_{4}+b_{5}+b_{6}+\mu _1\right) \left( d_{1}+d_{2}+d_3+d_{4}+d_{5}+d_{6}+\mu \right) }{\alpha \beta },\\ {\overline{I}}&= \frac{\alpha \beta \omega - \mu \left( b_{1}+b_{2}+b_3+b_{4}+b_{5}+b_{6}+\mu _1\right) \left( d_{1}+d_{2}+d_3+d_{4}+d_{5}+d_{6}+\mu \right) }{\alpha \beta \left( d_{1}+d_{2}+d_3+d_{4}+d_{5}+d_{6}+\mu \right) },\\ {\overline{V}}&= \frac{\alpha \beta \omega - \mu \left( b_{1}+b_{2}+b_3+b_{4}+b_{5}+b_{6}+\mu _1\right) \left( d_{1}+d_{2}+d_3+d_{4}+d_{5}+d_{6}+\mu \right) }{\beta \left( b_{1}+b_{2}+b_3+b_{4}+b_{5}+b_{6}+\mu _1\right) \left( d_{1}+d_{2}+d_3+d_{4}+d_{5}+d_{6}+\mu \right) }. \end{aligned}$$

Broadly we consider two kinds of interventions for this comparative effectiveness study.

  1. 1.

    Drugs that inhibit viral replication: Each of the four interventions Arbidol, Remdesivir, Interferon, Lopinavir/Ritonavir does this job. So we now choose \(\alpha\) to be \(\alpha (1-\epsilon _1)(1-\epsilon _2)(1-\epsilon _3)(1-\epsilon _4)\), where, \(\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4\) are chosen based on the efficacy of the drugs Arbidol, Remdesivir, Interferon and Lopinavir/Ritonavir, respectively.

  2. 2.

    Drugs that block virus binding to susceptible cells : Arbidol does this job. So we now choose \(\beta\) to be \(\beta (1-\gamma )\), where \(\gamma\) is the efficacy of the drug Arbidol in blocking virus binding to susceptible cells.

\({\mathcal {R}}_{0}\) plays a crucial role in understanding the spread of infection in the individual, and \({\overline{V}}\) determines the infectivity of the virus in an individual. Taking the two kinds of interventions into consideration, we now have a modified basic reproductive number \({\mathcal {R}}_{E}\) and a modified virus count \({\overline{V}}_{E}\) of the endemic equilibrium as follows:

$$\begin{aligned} {\mathcal {R}}_{E}&= \frac{ \alpha (1-\epsilon _1)(1-\epsilon _2)(1-\epsilon _3)(1-\epsilon _4) \beta (1-\gamma ) \omega }{\mu (b_{1}+b_{2}+b_3+b_{4}+b_{5}+b_{6}+\mu _1)(d_{1}+d_{2}+d_3+d_{4}+d_{5}+d_{6}+\mu )}, \\ \overline{V_{E}}&= \frac{\alpha (1-\epsilon _1)(1-\epsilon _2)(1-\epsilon _3)(1-\epsilon _4) \omega }{ \left( b_{1}+b_{2}+b_3 +b_{4}+b_{5}+b_{6}+\mu _1\right) \left( d_{1}+d_{2}+d_3+d_{4}+d_{5}+d_{6}+\mu \right) } \\&- \frac{ \mu }{\beta (1-\gamma )}. \end{aligned}$$

The efficacy of these interventions are taken based on hazard ratios. We first fix the value of \(\epsilon _1\) to be 0.7. From Table 3 we see that the hazard ratio of Remdesivir is \(44.5\%\) more than that of Arbidol therefore, we take the value of \(\epsilon _2\) to be 44.5 \(\%\) less than that of the efficacy of Arbidol (i.e. \(\epsilon _1\) ). The hazard ratio of INF is 12 \(\%\) more than that of Remdesivir, therefore the value of \(\epsilon _3\) is chosen 12 \(\%\) less than that of Remdesivir and similarly the value of \(\epsilon _4\) is chosen 6 \(\%\) less than that of \(\epsilon _3\). Based on these the values of \(\epsilon _1\), \(\epsilon _2\), \(\epsilon _3\), and \(\epsilon _4\) are taken to be 0.7, 0.38, 0.334, and 0.313 respectively. The efficacy of the drug Arbidol blocking virus binding to susceptible cells is taken to be 0.3. For comparative effectiveness study the parameter values are taken from Table 8 with \(\mu = 0.01.\)

Table 8 Parameter values
Full size table

We now do the comparative effectiveness study of these interventions by calculating the percentage reduction of \({\mathcal {R}}_0\) and \({\overline{V}}\) for single and multiple combination of these interventions. Percentage reduction of \({\mathcal {R}}_0\) and \({\overline{V}}\) are given by:

percentage reduction of \({\mathcal {R}}_{0} = \bigg [ \frac{{\mathcal {R}}_{0} - {\mathcal {R}}_{E_{j}}}{{\mathcal {R}}_{0}} \bigg ] \times 100\),

percentage reduction of \({\overline{V}} = \bigg [ \frac{{\overline{V}} - {\overline{V}}_{E_j}}{{\overline{V}}} \bigg ] \times 100\),

where j stands for \(\epsilon _1,\epsilon _2,\epsilon _3,\epsilon _4,\gamma\) or combinations thereof.

Since we have 4 drugs, we consider 16 (\(= 2^4\)) different combinations of these drugs.

Table 9 Comparative Effectiveness Study
Full size table

In the Table 9 the comparative effectiveness is calculated and measured on a scale from 1 to 16, with 1 denoting the lowest comparative effectiveness while 16 denoting the highest comparative effectiveness. The conclusions from this study are the following.

  1. 1.

    When single drug/intervention is administered, Arbidol outperforms other drugs/interventions w.r.t reducing both \({\mathcal {R}}_{0}\) and \({\overline{V}}\) (refer rows 2 to 5 in Table 9).

  2. 2.

    When two drugs/interventions are administered, the Remdesivir and Arbidol combination performs better than any combination of two drugs/interventions in reducing \({\mathcal {R}}_{0}\) and \({\overline{V}}\) (refer rows 6 to 11 in Table 9).

  3. 3.

    When three drugs/interventions are administered, the Remdesivir, Interferon and Arbidol combination performs better than any combination of three drugs/interventions in reducing \({\mathcal {R}}_{0}\) and \({\overline{V}}\) (compare rows 12 to 15 in Table 9).

  4. 4.

    The best reduction in \({\mathcal {R}}_{0}\) and \({\overline{V}}\) is seen (compare row 16 in Table 9) when all the four drugs/interventions are applied in combination.

8 Discussions and Conclusions

In this work we have considered four drug interventions, namely Arbidol, Remdesivir, Interferon and Lopinavir/Ritonavir, and studied their efficacy for treatment of COVID-19 when applied individually or in combination. This study is done in two ways.

   The first study modeled these interventions as control interventions and studied the optimal control problem. In this approach we derived an optimal control over a period of 30 days for the dynamics of susceptible and infected cells and virus load in the human body suffering of a COVID-19 infection. The second part of the study focused on the comparative effectiveness of the drugs in reducing the value of \(R_0\) and the viral load.

Conclusions from the optimal control studies and comparative effectiveness studies suggest the following.

  1. 1.

    All the drugs when administered individually or in combination reduce the infected cells and viral load significantly.

  2. 2.

    The average infected cell count and viral load decrease the most when all four interventions were applied together.

  3. 3.

    The average susceptible cell count decrease the most when Arbidol alone was administered.

  4. 4.

    The highest reduction in basic reproduction number and viral count is obtained when all four drugs/interventions are applied in combination.

The use of a combination of interventions was already in use for other viral diseases such as HIV (Kirschner and Webb 1997; Mbuagbaw et al. 2016; Yang et al. 2020; Montaner et al. 2001). In the works (Kirschner and Webb 1997; Yang et al. 2020) the combination of reverse transcriptase inhibitor and protease inhibitor were tried with sustained levels of CD4+. Currently, the combined chemotherapy named Highly Active Anti-Retroviral Therapy (HAART) is the most recommended chemotherapy for HIV infection (Thompson et al. 2012). Some of the studies on COVID-19 where the effectiveness of the control strategies are studied can be found in Nana-Kyere et al. (2022), Chaharborj et al. (2021), Madubueze et al. (2020). These studies are optimal control studies at the between-host or population level. To the best of our knowledge there are no optimal control studies at cellular level that discusses the effectiveness of specific antiviral drugs and immunomodulators. In Chhetri et al. (2021), we have developed a within-host model and discussed a general optimal control. The present work is an extension of our work (Chhetri et al. 2021) with specific control strategies at within-host level. The choice of the values of weight constants associated with control variables can play a very important role in determining the way in which the control acts. In this study we have chosen these values based on hazard ratio. The values of the weight constants are chosen high if the control associated with it is has low hazard ratio. Since the primary objective of this study is to study the role and effectiveness of combined drug therapy we do not explore the roles of different values of the weight constants.

In conclusion we state that the optimal strategy involves application of all four drugs simultaneously, resulting in the best possible minimization of the infection and the viral load. Due to this combined therapy there could possibly be side effects on organs such as liver and heart. The authors wish to address these issues in their future works. But here we wish to reinstate the fact that COVID-19 infection related cases can be reduced the best with a combined therapy. Even with side effects this strategy can be tried as implemented in other infections such as HIV, as survival of the patient is prime concern.