On the Effect of Age-Dependent Mortality on the Stability of a System of Delay-Differential Equations Modeling Erythropoiesis

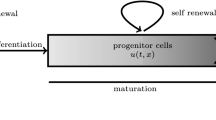
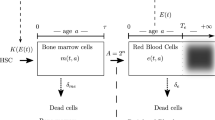
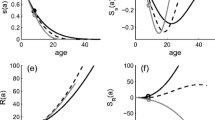
Abstract

We present an age-structured model for erythropoiesis in which the mortality of mature cells is described empirically by a physiologically realistic probability distribution of survival times. Under some assumptions, the model can be transformed into a system of delay differential equations with both constant and distributed delays. The stability of the equilibrium of this system and possible Hopf bifurcations are described for a number of probability distributions. Physiological motivation and interpretation of our results are provided.

Appendix A: Numerical Methods

In this section, we briefly describe the numerical methods behind the result of Sect. 3.2, which is adapted from Brunner et al. (1997) and Makroglou and Kuang (2006). Our goal is to compute a numerical solution to the following integro-differential equation

$$\begin{aligned} \frac{dE(t)}{dt} = {\mathcal {F}}\left( M(t)\right) - kE(t), \quad M(t) = \int\limits _{-\infty }^t e^{\beta \mu _1} S_0(E(\sigma -\mu _F)) l(t-\sigma ) d\sigma , \end{aligned}$$

(A.1)

on some finite time interval $0 \le t \le t_f$ given any constant initial and past hormone level $E(t) = E_0$, with $t \le 0$. Now let us consider the equidistant mesh $t_j = jh$ with $j = 0,\dots ,N$ and $h = t_f/N$, and let us furthermore suppose that the discrete maturation delay may be written as an integer multiple of the time-step as $\mu _F = Lh, \, L \in {\mathbb {N}}$. Applying a second-order Runge–Kutta scheme alongside with trapezoidal integration yields a system of 2N equations given by

$$\begin{aligned} \begin{aligned} M_j&= e^{\beta \mu _1} S_0(E_0) \int\limits _{-\infty }^0 l(t_j-\sigma ) d\sigma + h\sum _{i=0}^j \alpha _i e^{\beta \mu _1} S_0(E_{i-L})l(t_j - t_i), \\ E_j&= \frac{2}{2+hk}E_{j-1} + \frac{h}{2 + hk}\left( {\mathcal {F}}(M_{j-1}) + {\mathcal {F}}(M_j) - k E_{j-1} \right) , \\ \end{aligned} \end{aligned}$$

(A.2)

for the unknowns $(M_j,E_j)$, $j = 1,\ldots ,N$. We remark that in Eq. (A.2), $E_{i-L} = E_0$ if $i \le L$ while the $\alpha _i$ are the usual weights for trapezoidal quadrature defined by,

$$\begin{aligned} \alpha _i = {\left\{ \begin{array}{ll} \frac{1}{2} &{} \quad i = 0 \text { or } N, \\ 1 &{} \quad 0< i < N. \end{array}\right. } \end{aligned}$$

(A.3)

Fortunately, the presence of the discrete maturation delay makes it possible to explicitly solve the system A.2 given any constant initial and past hormone level $E_0$.