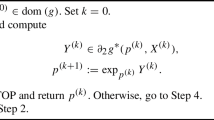Skip to main content
SpringerLink
Log in

On the Average Taxicab Distance Function and Its Applications

  • Published:
Acta Applicandae Mathematicae Aims and scope Submit manuscript

Abstract

Generalized conics are subsets in the space all of whose points have the same average distance from a given set of points (focal set). The function measuring the average distance is called the average distance function (or the generalized conic function). In general it is a convex function satisfying a kind of growth condition as the preliminary results of Sect. 2 show. Therefore any sublevel set is convex and compact. We can also conclude that such a function has a global minimizer.

The paper is devoted to the special case of the average taxicab distance function given by integration of the taxicab distance on a compact subset of positive Lebesgue measure in the Euclidean coordinate space.

The first application of the average taxicab distance function is related to its minimizer. It is uniquely determined under some natural conditions such as, for example, the connectedness of the integration domain. Geometrically, the minimizer bisects the measure of the integration domain in the sense that each coordinate hyperplane passing through the minimizer cuts the domain into two parts of equal measure. The convexity and the Lipschitzian gradient property allow us to use the gradient descent algorithm that is formulated in terms of a stochastic algorithm (Sect. 3) to find the bisecting point of a set in \(\mathbb{R}^{n}\).

Example 1 in Sect. 4 shows the special form of the average taxicab distance function of a convex polygon. The level curves (generalized conics) admit semidefinite representations as algebraic curves in the plane because the average taxicab distance function is piecewise polynomial of degree at most three.

Some applications in geometric tomography are summarized as our main motivation to investigate the concept of the average taxicab distance function. Its second order partial derivatives give the coordinate \(X\)-rays of the integration domain almost everywhere and vice versa: the average taxicab distance function can be expressed in terms of the coordinate \(X\)-rays. Therefore the reconstruction of the sets given by their coordinate \(X\)-rays can be based on the average taxicab distance function instead of the direct comparison of the \(X\)-rays. In general (especially, in some classes of non-convex sets), the convergence property of the average taxicab distance function with respect to the Hausdorff convergence of the integration domain is better than the convergence of the \(X\)-rays (see regular and \(X\)-regular convergences in Sect. 4.1) and we can apply a standard approximation paradigm (Footnote 1) to solve the problem.

In the last section we prove that any compact convex body is uniquely determined by the diagonalization of its covariogram function measuring the average taxicab distance of the points from the intersection of the body with the translates of its axis parallel bounding box.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. Convergence properties are very important from the viewpoint of approximation processes: let \(M\) be a compact metric space and suppose that the element \(x\in M\) is given in an implicit way \({\varPhi(x)=y}\). If the mapping \(\varPhi\) is continuous then its set-valued inverse is automatically upper semi-continuous. Especially, for any \(\varepsilon> 0\) there exists \(\delta> 0\) such that \(\inf_{x^{*}\in\varPhi^{-1}(y)} \operatorname{dist}(z, x^{*})< \varepsilon\) provided that \(\operatorname{dist}(y,\varPhi(z))< \delta\). This means that \(z\) approximates at least one of the elements in \(\varPhi^{-1}({\mathbf{y}})\).

  2. The phrase “generalized conic function” goes back to the classical concept of conics: an ellipse is the level set of a function measuring the arithmetic mean of distances from the elements of a set containing exactly two different points.

  3. More precisely, we should write that \(\mathbb{E}(Z_{k+1} | F_{k})\leq Z_{k}\), where \(F_{k}\) is the \(\sigma\)-algebra generated by \(X_{0}, \ldots, X_{k}\) and \(Q_{1}, \ldots, Q_{k}\) but it can be easily seen that \(\mathbb{E}(Z_{k+1} | F _{k})=\mathbb{E}(Z_{k+1} | X_{k})\).

References

  1. Barczy, M., Nagy, Á., Noszály, Cs., Vincze, Cs.: A Robbins-Monro type algorithm for computing the global minimizer of generalized conic functions. Optimization 64(9), 1999–2020 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bianchi, G., Burchard, A., Gronchi, P., Volcic, A.: Convergence in shape of Steiner symmetrization. Indiana Univ. Math. J. 61(4), 1695–1709 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bouleau, N., Lépingle, D.: Numerical Methods for Stochastic Processes. Wiley, New York (1994)

    MATH  Google Scholar 

  4. Gardner, R.J., Kiderlen, M.: A solution to Hammer’s X-ray reconstruction problem. Adv. Math. 214, 323–343 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  5. Podkorytov, A.N., Minh, M.V.: On the inversion formula of the Fourier transform of the characteristic function of several variables. J. Math. Sci. 120(2), 1191–1194 (2015)

    Article  MathSciNet  Google Scholar 

  6. Vincze, Cs., Nagy, Á.: An introduction to the theory of generalized conics and their applications. J. Geom. Phys. 61(4), 815–828 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  7. Vincze, Cs., Nagy, Á.: On the theory of generalized conics with applications in geometric tomography. J. Approx. Theory 164, 371–390 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  8. Vincze, Cs., Nagy, Á.: Reconstruction of hv-convex sets by their coordinate X-ray functions. J. Math. Imaging Vis. 49(3), 569–582 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  9. Vincze, Cs., Nagy, Á.: Generalized conic functions of hv-convex planar sets: continuity properties and X-rays. Aequ. Math. 89(4), 1015–1030 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  10. Vincze, Cs., Nagy, Á.: An algorithm for the reconstruction of hv-convex planar bodies by finitely many and noisy measurements of their coordinate X-rays. Fundam. Inform. 141(2–3), 169–189 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics, University of Debrecen, P.O. Box 400, 4002, Debrecen, Hungary

    Csaba Vincze

  2. Institute of Mathematics, MTA-DE Research Group “Equations, Functions and Curves”, Hungarian Academy of Sciences and University of Debrecen, P.O. Box 400, 4002, Debrecen, Hungary

    Ábris Nagy

Authors
  1. Csaba Vincze
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ábris Nagy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Csaba Vincze.

Additional information

Cs. Vincze is supported by the EFOP-3.6.2-16-2017-00015 project. Á. Nagy is supported by the Hungarian Academy of Sciences. The project has been supported by the European Union, co-financed by the European Social Fund.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vincze, C., Nagy, Á. On the Average Taxicab Distance Function and Its Applications. Acta Appl Math 161, 201–220 (2019). https://doi.org/10.1007/s10440-018-0210-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10440-018-0210-1

Keywords

Mathematics Subject Classification

Search

Navigation