1 Introduction

Living cells are soft and complex materials with cytoskeletons continuously subjected to highly dynamic remodeling. Their mechanical properties have been found to be related to various cellular physiology behaviors, including cell locomotion [1], differentiation [2], adhesion [3, 4] and nanoparticle endocytosis [5,6,7]. In addition, it has been widely revealed that many human diseases also have close relationships with the mechanical properties of corresponding cells [8,9,10,11,12,13]. For example, the malaria-infected red blood cells can become stiffer and sticky, which are unfavorable for the oxygen transport, eventually leading to severe anemia, coma or even death [12]. Therefore, precise measurement of the mechanical properties of living cells can be very crucial for diagnosing human disease and better understanding biological processes.

Quantitative measurement of material properties of living cells is usually difficult due to the facts of their low stiffness, small size and severe thermal fluctuations. Despite these difficulties, a series of experimental efforts have been conducted to probe the mechanical properties of living cells by using various techniques, including the atomic force microscopy (AFM) [14,15,16,17,18], magnetic twisting cytometry [19], magnetic or optical tweezers [20], microplate rheometer [21] and particle tracking microrheology [22, 23]. In these measurements, indentation techniques based on the AFM were most popularly adopted. As long as the force–indentation curves are measured by using the AFM, the Hertz contact calibration model based on the isotropic elastic theory is usually introduced to fit them. Material constants of cells are determined as fitting parameters [14,15,16,17]. However, as cells are complex living materials, thermal fluctuations and cytoskeleton remodeling often enable them to exhibit both solid-like property of elasticity and fluid-like behavior of viscidity. Usually, under such a situation, the material constants of cells cannot be uniquely determined by simply using the elastic constitutive relation in the AFM measurements. For example, it has been reported that the Young’s moduli of two types of breast cancer cells exhibit strong dependence on loading rates in the AFM experiments [17].

There have been many studies attempting to determine the viscoelastic property of cells in terms of the traditional systems of Hookean springs and Newtonian viscous dashpots [24, 25]. However, the cytoskeletons of cells are complex polymer networks comprised of polymers with randomly distributed lengths, bending rigidities, orientations and entanglement densities, which usually make the characteristic time scales of creep and relaxation determined from exponential decays widely distributed and infinite in number. We can imagine that the spring-dashpot-type models of viscoelasticity for cells cannot be accurate unless a sufficient number of elements of springs and dashpots are introduced. For example, Susana et al. [24] used a spring-dashpot model with five parameters to fit the indentation curves of MCF-7 cells. Recently, cell-type-specific power-law behaviors have been observed in various types of cultured cells with different measurement techniques when analyzed over certain time scales [21, 26]. Although such a power-law treatment seems capable of capturing the essential nature of living cells under indentation, it is still far from complete in facilitating unique viscoelastic constitutive relations for general living cells. As has been pointed out by Bu et al. [27], there exist two critical issues in determining the linear constitutive relations of the cells. The first one is that both the behaviors of deformation creep and stress relaxation of a cell should be measured. The second one is that a convolution relation between the measured creep compliance and relaxation modulus should be verified so that whether or not the cell is a linear viscoelastic material can be justified. The reason for such verification is that cells as materials are generally nonlinear, although most of them are nearly linear over certain ranges of some variables of stress, strain, time and temperature. Only after the cells have been confirmed to be linear viscoelastic materials, the constitutive relation and the material constants can be constructed and extracted in terms of the measured creep compliance and relaxation modulus.

In spite of the progresses mentioned above, so far, understanding is still poor in how the constitutive relation of viscoelasticity of each specific type of cells can be precisely determined. In this study, we focus on the measurements of deformation creep and force relaxation trajectories of six different human cell lines by using the technique of AFM indentation. From these trajectories, we determine the creep compliance and relaxation modulus of each cell line by using the classical spring-dashpot and the power-law models, respectively. Then, we determine which model gives the better fit and verify whether the determined pair of creep compliance and relaxation modulus satisfy the convolution relation derived from the linear viscoelastic theory, so that we can eventually determine whether or not this cell line is a linear viscoelastic material, and extract the material constants accordingly.

2 Materials and Methods

2.1 Cell Preparation

The present study focuses on the human normal gastric (GES-1), gastric cancer (SGC7901, NCI-N87), normal hepatic (L02), hepatic cancer (HepG2), and hepatic stellate (LX2) cell lines. For the purpose of routine culture, the hepatic cell lines were maintained at 37 \( {^{\circ }}\hbox {C}\) in a 5% CO2 incubator (Memmert, INE800749L, Germany), and the gastric cell lines were also maintained at the incubator (HealForce, HF90, China) with the same settings. For the AFM indentation, cells harvested from the subculture were seeded on sterilized 35-mm petri dishes which would stay in the incubator for 22–25 h prior to each indentation. The medium was changed with normal saline before the AFM indentation to clear extracellular secretion and dead cells.

2.2 AFM Indentation

A Nanowizard III BioScience AFM (JPK, Germany) was used for the indentation tests. A modified silicon nitride AFM cantilever (NovaScan, USA) with a spring constant of 0.01 N/m was used to indent the cells. A 4.5-\(\upmu \hbox {m}\) diameter polystyrene bead was adhered to the cantilever tip. The experiments were conducted at room temperature within 1 h per dish to ensure the bioactivity of cells. For all the AFM indentation measurements, the cantilever was always vertically approaching the nucleus areas of the cells at an ultrafast initial velocity of 50 \(\upmu \)m/s. Once a pre-defined force for the creep and pre-defined height for the relaxation are reached, the approaching is stopped by controlling the position of cantilever base. Subsequently, under such pre-defined constant force and height, the cantilever was kept in contact with the cells for 20 s, lying within the experimentally observed time range of about 0.01–100 s [28].

2.3 Deformation Creep and Stress Relaxation of Linear Viscoelastic Materials

We assume living cells as incompressible linear viscoelastic solids. Then, the corresponding constitutive equations can be written as [29]

$$\begin{aligned} \varepsilon _{ij} \left( t \right) =\int _0^t {J\left( {t-\tau } \right) \frac{\hbox {d}\sigma _{ij} \left( \tau \right) }{\hbox {d}\tau }\hbox {d}\tau } , \quad \sigma _{ij} \left( t \right) =\int _0^t {Y\left( {t-\tau } \right) \frac{\hbox {d}\varepsilon _{ij} \left( \tau \right) }{\hbox {d}\tau }\hbox {d}\tau } \end{aligned}$$
(1)

where \(J\left( t \right) \) is the creep compliance of the viscoelastic body, \(Y\left( t \right) \) the relaxation modulus, \(\varepsilon _{ij} \) and \(\sigma _{ij}\) are components of the strain and stress tensors, respectively. Applying the Laplace transform to Eq. (1) in terms of time, we obtain

$$\begin{aligned} \hat{{\varepsilon }}_{ij} =s\hat{{J}}\left( s \right) \hat{{\sigma }}_{ij} \left( s \right) , \quad \hat{{\sigma }}_{ij} =s\hat{{Y}}\left( s \right) \hat{{\varepsilon }}_{ij} \left( s \right) \end{aligned}$$
(2)

where \(\hat{{J}}\left( s \right) ,\ \hat{{Y}}\left( s \right) ,\ \hat{{\varepsilon }}_{ij} \left( s \right) \hbox { and }\hat{{\sigma }}_{ij} \left( s \right) \) are the Laplace transforms of \(J\left( t \right) \), \(Y\left( t \right) \), \(\varepsilon _{ij}\) and \(\sigma _{ij}\). From Eq. (2), we can easily deduce that \(\hat{{Y}}\left( s \right) =1/s^{2}\hat{{J}}\left( s \right) \), which corresponds to the following relation in real time space as [29]

$$\begin{aligned} \int _0^t {J\left( {t-\tau } \right) Y\left( t \right) \hbox {d}\tau =t} \end{aligned}$$
(3)

We note that Eq. (3) is derived based on the assumption of incompressible linear viscoelasticity. In the following sections, we will use this relation as the criterion to verify whether the mechanical properties of a living cell are linear, so that one can know whether or not the experimentally determined creep compliance and relaxation modulus can be used to construct the constitutive relation.

In practical applications of viscoelastic modeling, there exist many different models to specify the creep compliance and relaxation modulus in Eq. (1). Traditionally, the constitutive relation of a general linear viscoelastic solid can be represented by a network of linear combinations of springs and dashpots. Following such a spring-dashpot representation, the creep compliance and relaxation modulus can be expressed though a so-called Prony series [30, 31],

$$\begin{aligned} J\left( t \right) =\frac{1}{E}\left[ {1+\sum _{i=0}^m {c_i \left( {1-\hbox {e}^{-t/\tau _i }} \right) } } \right] ,Y\left( t \right) =E\left[ {1-\sum _{j=0}^n {d_j \left( {1-\hbox {e}^{-t/\tau ^{\prime }_j }} \right) } } \right] \end{aligned}$$
(4)

where E represents the initial Young’s modulus, \(\tau _i ,\tau ^{\prime }_j \) are the typical creep and relaxation time scales, m and n together are related to the number of springs and dashpots in the system. The Prony series in Eq. (4) are named as the m-th order and n-th order in this study, respectively.

We can see from Eq. (4) that the spring-dashpot type constitutive relations of the viscoelastic materials usually consist of a finite number of scales of the characteristic times for the creep and relaxation behaviors. If a large number of terms of Eq. (4) are required in accurately describing the mechanical behaviors of the materials, e.g., the living cells, then the expressions of Eq. (4) may become no longer practical as the coefficient of each term can be very hard to uniquely determine. However, like the soft glass rheology theory derived from soft matter physics, the viscoelastic spectrum of living cells lacks any distinct timescales that can be identified with discrete structural elements or processes, meaning that a large number of parameters will be inevitably involved to fit experimental measurements successfully by using Eq. (4). In order to resolve this problem, we adopt the power-law-type creep function as follows [29, 32]

$$\begin{aligned} J\left( t \right) =\frac{1}{E}\left( {t/\tau _0 } \right) ^{\beta } \end{aligned}$$
(5)

where E still represents the effective Young’s modulus at time \(\tau _0 \), then 1 / E becomes the elastic compliance, and \(\beta \) characterizes the degree of dissipation or “fluidity” of the viscoelastic material [32,33,34]. When \(\beta \) approaches zero, Eq. (5) becomes the inverse of material stiffness, corresponding to the deformation of a purely elastic solid. On the contrary, if \(\beta \) tends to unity, Eq. (5) becomes corresponding to the deformation of a purely viscous Newtonian fluid. For living cells, the measured \(\beta \) are typically located between 0.1 and 0.5 [32,33,34]. For incompressible linear viscoelastic materials, the relation in Eq. (3) must be satisfied. Then, the corresponding relaxation modulus can be determined from Eq. (3) as follows [27]

$$\begin{aligned} Y\left( t \right) =\frac{E}{\varGamma \left( {1+\beta } \right) \varGamma \left( {1-\beta } \right) }\left( {t/\tau _0 } \right) ^{-\beta } \end{aligned}$$
(6)

In the following sections, we will use the classical spring-dashpot model represented by Eq. (4), and the power-law model by Eqs. (5) and (6) to fit the experimental measurements on the creep and relaxation behaviors.

Fig. 1
figure 1

Schematic of the experimental setup for the indentation of a cell using spherical indenter probes

Full size image

2.4 AFM Measurements and Data Processing

Figure 1 shows the process of indentation of a single cell, where Z is the vertical height of the probe base, \(Z_0 \) the value of Z at the contact point, d the vertical deflection of the cantilever. In addition, we define \(\delta \) as the indentation depth and P the indentation force. If the spring constant of the cantilever is k, then we have

$$\begin{aligned} P=k\Delta d \end{aligned}$$
(7)

where

$$\begin{aligned} \delta =Z_0 -Z-\Delta d, \quad \Delta d=d-d_0 \end{aligned}$$
(8)

When the incompressible viscoelastic solid is indented by a rigid sphere with radius R, the relation between the indentation force and indentation depth can be expressed as [35,36,37]

$$\begin{aligned} P\left( t \right) =\frac{8\sqrt{R}}{3}\int _0^t {Y\left( {t-\tau } \right) \frac{\partial \left[ {\delta ^{3/2}\left( \tau \right) } \right] }{\partial \tau }} \hbox {d}\tau \end{aligned}$$
(9)

or

$$\begin{aligned} \delta ^{3/2}\left( t \right) =\frac{3}{8\sqrt{R}}\int _0^t {J\left( {t-\tau } \right) \frac{\partial P\left( \tau \right) }{\partial \tau }} \mathrm{d}\tau \end{aligned}$$
(10)

When a step external force or displacement is applied during the indentation, we have \(P\left( t \right) =P_0 H\left( t \right) \) and \(\delta \left( t \right) =\delta _0 H\left( t \right) \). Then, Eqs. (9) and (10) become [27, 35]

$$\begin{aligned} J\left( t \right) =\frac{8\sqrt{R}}{3P_0 }\delta \left( t \right) ^{3/2}\hbox { and }Y\left( t \right) =\frac{3}{8\sqrt{R}\delta _0 ^{3/2}}P\left( t \right) \end{aligned}$$
(11)
Fig. 2
figure 2

Creep and relaxation measurements on normal hepatic cells (L02): a creep of the Z-position of cantilever base under force-controlled loading; b relaxation of the indentation force under displacement-controlled loading

Full size image

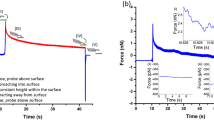
Figure 2 shows the time trajectories during the displacement creep and force relaxation experiments for the AFM indentation of normal hepatic cells. Figure 2a illustrates the creep test, in which the pre-defined indentation force is sustained at 0.88 nN for 20 s after the rapid loading and before unloading, while the Z-position decreases from \(11.89\,\upmu \hbox {m}\) to \(5.88\,\upmu \hbox {m}\) with time over 20 s. Figure 2b demonstrates the relaxation test, in which the Z-position is kept at \(6.91\,\upmu \hbox {m}\) after the rapid loading and before unloading, while the indentation force decreases from 1.9 nN to 0.7 nN over 20 s.

Fig. 3
figure 3

Normalized indentation depth of a human hepatic cell lines and c human gastric cell lines, and normalized indentation force of b human hepatic cell lines and d human gastric cell lines, where N is the number of cells used for the measurements

Full size image
Fig. 4
figure 4

Comparison of experimental results and the corresponding least-square fittings in terms of the power-law and spring-dashpot models for the creep compliance of a L02, c HepG2, and e LX2, and the relaxation modulus of b L02, d HepG2, and f LX2

Full size image
Fig. 5
figure 5

Comparison of experimental results and the corresponding least-square fittings in terms of the power-law and spring-dashpot models for the creep compliance of a GES-1, c NCI-N87, and e SGC7901, and the relaxation modulus of b GES-1, d NCI-N87, and f SGC7901

Full size image

3 Result and Discussion

We repeated the deformation creep and force relaxation tests for N times by using N different cells for each cell line. During each test, we recorded the indentation depth \(\delta \left( t \right) \) for the creep test, and the indentation force \(P\left( t \right) \) for the relaxation test, as a function of time. We performed ensemble average over N different trajectories to obtain the mean value of the normalized indentation depth of the 3/2 power, \(\left\langle {(\delta /\delta _0 )^{3/2}} \right\rangle \), and the normalized indentation force, \(\left\langle {P/P_0 } \right\rangle \). Figure 3 shows the comparison on \(\left\langle {(\delta /\delta _0 )^{3/2}} \right\rangle \) and \(\left\langle {P/P_0 } \right\rangle \) as functions of time for the hepatic (a, b) and gastric cells (c, d). It can be seen from Fig. 3a, b that the L02 and HepG2 cells show similar fluidity, while the LX2 cells appear more solid-like than them. This is not surprise since LX2 cells are the major cells involved in liver fibrosis, which is the formation of scar tissue in response to liver damage. However, for the gastric cell lines in Fig. 3c, d, the creep and relaxation results give contradictory predictions. For example, Fig. 3c indicates that the fluidity of the three gastric cell lines is in the order of NCI-N87 > SGC7901 > GES-1 according to the creep test, while Fig. 3d shows an opposite trend in terms of the relaxation test. These unreasonable results imply that at least two of the three cell lines are nonlinear materials, leading to wrong predictions of mechanical properties based on the linear theory. This fact indicates that one cannot simply use the experimental results of either creep or relaxation to describe the mechanical properties of living cells without verifying whether the creep compliance and relaxation modulus satisfy the linearity requirement in Eq. (3).

In order to predict the creep compliance and relaxation modulus from the indentation test for different cell lines, we consider the ensemble average on both sides of Eq. (11), which gives

$$\begin{aligned} \left\langle {J\left( t \right) } \right\rangle =\left\langle {\frac{8\sqrt{R}}{3P_0 }\delta \left( t \right) ^{3/2}} \right\rangle \hbox { and }\left\langle {Y\left( t \right) } \right\rangle =\left\langle {\frac{3}{8\sqrt{R}\delta _0 ^{3/2}}P\left( t \right) } \right\rangle \end{aligned}$$
(12)
Table 1 Least-square fitting parameters for the power-law model, \(\varvec{e=1\times 10^{-3}}\)
Full size table
Table 2 Least-square fitting parameters for the spring-dashpot model in terms of the first-order Prony series, \(\varvec{e=1\times 10^{-3}}\)
Full size table
Table 3 Least-square fitting parameters for the spring-dashpot model in terms of the second-order Prony series, \(\varvec{e=1\times 10^{-3}}\)
Full size table
Fig. 6
figure 6

Convolution of the experimentally measured creep compliance and relaxation modulus of a L02, b HepG2, c LX2, d GES-1, e NCI-N87, and f SGC7901 cells

Full size image

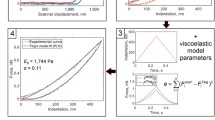
The solid squares in Figs. 4 and 5 show the experimental results on the average values of creep compliance and relaxation modulus as functions of time for both hepatic (Fig. 4) and gastric (Fig. 5) cells. These experimental data can be fitted by the classical spring-dashpot model and the power-law-type model, as shown in Eqs. (4–6). By using the least-square fitting method, Tables 1, 2 and 3 list the fitting parameters of the power-law and spring-dashpot models in terms of the creep experiments. Interestingly, the results of fitted effective elastic compliance 1/E for all the cell lines are almost not affected by the model selection. In contrary, values of the fitted characteristic time scales, \(\tau _i \), in terms of the spring-dashpot model, even exhibit differences in orders of magnitudes. Further studies are therefore needed for understanding the relation between such large discrepancies and the corresponding biological appearances of cells.

Figures 4a, c, e and 5a, c, e show the comparison between the experimental results on creep compliance and the least-square fittings of the experimental data by using the power-law and spring-dashpot models in terms of the 1\(^{\mathrm{st}}\)-order and 2\({\mathrm{nd}}\)-order Prony series with the fitting parameters listed in Tables 1, 2 and 3. It can be seen from Figs. 4a, c, e and 5a, c, e that the 3-parameter power-law model can fit all the experimental results very well, the fitting results based on the 3-parameter spring-dashpot model show large discrepancies with experiments, and those based on the 5-parameter spring-dashpot model seem close to the experiments. However, we can see from Figs. 4a, c, e and 5a, c, e that the fitting results based on the 5-parameter spring-dashpot model show unrealistic sharp turning points or large slops at times close to the corresponding time scales \(\tau _{1}\) in Table 3 for each cell line.

Once the creep compliance is obtained by fitting the creep experiments, the relaxation modulus is obtained by applying the fitting parameters in Tables 1, 2 and 3 to Eqs. (4–6). Figures 4b, d, f and 5b, d, f show the comparison between the experimental results on relaxation modulus and the theoretical predictions based on the power-law and spring-dashpot models in terms of the fitting parameters in Tables 1, 2 and 3. It can be seen from Figs. 4b, d, f and 5b, d, f that the theoretical predictions agree with the experiments very well for cell lines of L02, HepG2, LX2 and NCI-N87, but not for GES-1 and SGC7901. This comparison implies that L02, HepG2, LX2 and NCI-N87 are linear viscoelastic materials, and GES-1 and SGC7901 are nonlinear.

In order to further verify which cell line is linear or nonlinear, we consider the derived relation in Eq. (3). Once we have experimentally obtained the creep compliance and the relaxation modulus as functions of time, \(J\left( t \right) \) and \(Y\left( t \right) \), we can numerically calculate their convolution, \(J\left( t \right) *Y\left( t \right) \), then perform ensemble average to obtain \(<J\left( t \right) *Y\left( t \right)>\). We compare the experimentally determined \(\langle J\left( t \right) *Y\left( t \right) \rangle \) with the function t. The linear viscoelasticity of a material needs these two functions to be identical. Otherwise, the material must be nonlinear. Figure 6 shows such comparisons. We can see from Fig. 6 that the convolutions, \(\langle J\left( t \right) *Y\left( t \right) \rangle \), for the cell lines of L02, HepG2, LX2 and NCI-N87 are close to the function t, but those for GES-1 and SGC7901 show obvious discrepancies. In order to give a quantitative estimation on such a discrepancy, we calculate \(\left( {\langle J\left( t \right) *Y\left( t \right) >rlangle t} \right) /t\) for each cell line. The values are 7% to 13.1% for L02, − 14.6% to − 4.8% for HepG2, − 2.8% to 2.7% for LX2, and − 5.5% to 2% for NCI-N87. However, such a value becomes − 54.7% to − 42.6% for GES-1, and − 38.7% to − 21.7% for SGC7901. Therefore, it can be easily deduced that the cell lines of NCI-N87 and GES-1 show obvious nonlinear material properties. For these two cell lines, one cannot simply use the linear viscoelastic constitutive relation to predict their mechanical behaviors.

4 Conclusions

In summary, we have used the AFM to measure the deformation creep and force relaxation trajectories of six different human cell lines. Based on these measurements, we have determined the creep compliance and relaxation modulus of these cells by the technique of least-square fitting in terms of the power-law and spring-dashpot models, respectively. We found that the 3-parameter power-law model can fit the experiments very well. For the spring-dashpot model, only when the fitting parameters are at least 5, then the fitting results can be acceptable, but there still exist unexpected sharp turns in the fitting curves. We have further verified whether the measured creep compliance and relaxation modulus satisfy the convolution relation derived from the linear viscoelastic theory, by which one can know whether a cell line follows a linear constitutive relation. We found that the human normal hepatic (L02), hepatic cancer (HepG2), hepatic stellate (LX2) and gastric cancer (NCI-N87) cell lines are linear viscoelastic materials, and human normal gastric (GES-1) and gastric cancer (SGC7901) cell lines are nonlinear. The obtained fitting parameters can be used as the corresponding material constants for the former, but not the latter. Not only the material constants, for the cell lines with nonlinear mechanical properties, like GES-1 and SGC7901, the simple creep and relaxation behaviors can even give contradictory predictions on their mechanical properties and behaviors.