Introduction

An equatorial plasma bubble (EPB) is a plasma density depletion area or structure that mainly occurs in the equatorial and low-latitude ionosphere. The mechanism behind the formation of EPB is believed to be the Rayleigh–Taylor instability. After sunset, the eastward electric field enhances in reverse (namely pre-reverse enhancement) and uplifts the ionospheric F layer, producing a fine condition for Rayleigh–Taylor instability (Kelly 2009). If a large-scale wave structure, known as a seed, exists at the bottom side of the F layer, the EPB will generate and propagate upward to the topside ionosphere and also to low latitudes even middle latitudes along the magnetic field lines (Tsunoda 2010; Smith and Heelis 2017). Generally, the EPB occurrence is positively correlated to the solar activity and shows a seasonal difference which is more frequent during spring and autumn equinoxes (Nishioka et al. 2008; Aa et al. 2020).

EPB exerts a severe threat to radio signals across the ionosphere, affecting widely used global navigation satellite system (GNSS). The irregularities in electron density associated with EPB can cause scintillation, which refers to rapid fluctuations in the amplitude and phase of GNSS signals passing through the ionosphere (Kintner et al. 2007). Ionospheric scintillation can increase the GNSS measurement noise and even lead to loss of satellite signal lock in serious cases (Skone et al. 2001; Srinivasu et al. 2022), then degrading positioning results (Dubey et al. 2006; Aquino et al. 2009). Except the ionospheric scintillation, EPB can also create strong plasma gradients in ionosphere, which has adverse effects on GNSS techniques relied on precise ionospheric corrections (Affonso et al. 2022).

Many studies have reported the effects of EPB and its related ionospheric scintillation on GNSS precise point positioning (PPP), which is a stand-alone positioning technique that takes into account a range of error sources and corrects them to provide highly accurate positioning results (Zumberge et al. 1997; Kouba and Héroux 2001). Moreno et al. (2011) indicated the estimated altitude errors were up to several meters for a single-epoch PPP at equatorial latitudes of Africa after sunset. Luo et al. (2018) reported the 3D root-mean-square (RMS) of GNSS PPP was 1.842 m under scintillation condition using station in Hong Kong. Zakharenkova and Cherniak (2021) presented the 3D error of kinematic PPP for the stations in the America rose to several meters due to the effects of storm-induced EPBs.

An advanced GNSS PPP technique is so-called PPP with real-time kinematic (PPP-RTK) that employs the extra error data such as ionospheric corrections to obtain highly accurate positioning results quickly (Wübbena et al. 2005; Li et al. 2022a). Obviously, GNSS PPP-RTK technique is also susceptible to the impact of EPB-induced ionospheric scintillation. Furthermore, different from the general PPP technique, PPP-RTK relies on precise ionospheric correction constraint. The ionospheric gradients generated by EPB can degrade the accuracy of ionospheric corrections, thereby might also exerting impact on the estimated results of PPP-RTK. In this study, we further investigate the effects of EPB-induced ionospheric gradients on GNSS PPP-RTK. To our knowledge, related study is still not involved.

Methodology

When a user employs the PPP-RTK technique to calculate the position, the precise ionospheric correction constraint on the user side is necessary. Generally, the ionospheric information on the user side can be obtained using the inverse distance weighting algorithm (Shepard 1968) to interpolate the ionospheric corrections of three reference stations close to the user,

$$TEC_{u,p}^{s} = \frac{{\mathop \sum \nolimits_{i = 1}^{3} TEC_{r,i}^{s} \cdot w_{r,i} }}{{\mathop \sum \nolimits_{i = 1}^{3} w_{r,i} }}, w_{r,i} = \frac{1}{{d_{r,i} }}$$
(1)

where \(s\) is the satellite number, \(TEC_{u,p}^{s}\) is the ionospheric total electron content (TEC) on the user side by interpolation, \(TEC_{r,i}^{s}\) and \(w_{r,i}\) are the ionospheric TEC and its weight on the reference station \(i\), \(d_{r,i}\) is the distance between the user station and the reference station \(i\). Here, we use the TEC value to represent the ionospheric correction. The unit of TEC is TECU (1 TECU = 1016/m2).

To assess the accuracy of \(TEC_{u,p}^{s}\), a reference station with known ionospheric TEC \(TEC_{u,o}^{s}\) is served as a user station. Then the ionospheric residual \(\delta TEC_{u}^{s}\) can be calculated as follows

$$\delta TEC_{u}^{s} = TEC_{u,o}^{s} - TEC_{u,p}^{s}$$
(2)

If an EPB occurs, the observed ionospheric TEC is deviated from its normal or background value due to TEC depletion. Considering the TEC variation by EPB and letting \(TEC_{u,o}^{s} = TEC_{u,o}^{\prime s} + dTEC_{u,o}^{s} \;and\;TEC_{u,p}^{s} = TEC_{u,p}^{\prime s} + dTEC_{u,p}^{s}\), equation (2) can be rewritten as follows

$$\begin{aligned} \delta TEC_{u}^{s} & = \left( {TEC_{u,o}^{\prime s} + dTEC_{u,o}^{s} } \right) - \left( {TEC_{u,p}^{\prime s} + dTEC_{u,p}^{s} } \right) \\ = \left( {TEC_{u,o}^{\prime s} - TEC_{u,p}^{\prime s} } \right) + \left( {dTEC_{u,o}^{s} - dTEC_{u,p}^{s} } \right) \\ \end{aligned}$$
(2a)

where \(TEC_{u,o}^{\prime s}\) is the background TEC on user station, \(TEC_{u,p}^{\prime s}\) is the weighted average of background TEC on three reference stations by (1), \(dTEC_{u,o}^{s}\) is the magnitude of TEC variation on user station, \(dTEC_{u,p}^{s}\) is the weighted average of TEC variations on three reference stations by (1).

According to (2a), the ionospheric residual induced by EPB \(dTEC_{u}^{s}\) can be calculated as follows

$$\delta \;dTEC_{u}^{s} = dTEC_{u,o}^{s} - dTEC_{u,p}^{s}$$
(3)

The TEC variation can be extracted from the observed TEC time-series using the method developed by Tang et al. (2021). This method finds the EPB occurrence time according to the rate of TEC index (Pi et al. 1997), and then fits the background TEC during EPB event using a low-order polynomial. Finally, the TEC variation during EPB event is obtained by subtracting the observed TEC from the background TEC.

It should be pointed out that the known ionospheric corrections \(TEC_{r,i}^{s}\) and \(TEC_{u,o}^{s}\) are estimated using PPP technique, which include satellite and receiver differential code biases (DCBs) (Zhang et al. 2012). The satellite DCBs can be corrected by precise products. To remove the receiver DCBs, single-difference-between-satellite strategy is employed in PPP-RTK solution (Li et al. 2022b). So, the final ionospheric residual is also the differenced result between satellites.

According to (2a) and (3), the single-difference-between-satellite ionospheric residual \(TEC_{u}^{b,j}\) and its part by EPB \(\nabla \delta dTEC_{u}^{b,j}\). can be calculated as follows

$$\left\{ {\begin{array}{*{20}c} {\nabla \delta TEC_{u}^{b,j} = \delta TEC_{u}^{b} - \delta TEC_{u}^{j} } \\ {\nabla \delta dTEC_{u}^{b,j} = \delta dTEC_{u}^{b} - \delta dTEC_{u}^{j} } \\ \end{array} } \right.$$
(4)

where \(b\) and \(j\) are the reference satellite and other satellite,\(\delta TEC_{u}^{b}\) and \(\delta TEC_{u}^{j}\) are the un-differenced ionospheric residuals of satellite \(b\) and \(j\), \(\delta dTEC_{u}^{b}\) and \(\delta dTEC_{u}^{j}\) are the un-differenced ionospheric residuals induced by EPB of satellite \(b\) and \(j\), respectively. Hereinafter, we just use the ionospheric residual to call the single-difference-between-satellite ionospheric residual for simplicity.

In PPP-RTK processing, two modes, namely \(\nabla \delta dTEC_{u}^{b,j}\) correction and non-correction, are executed to evaluate the effects of EPB-induced ionospheric gradients on estimated 3D positions.

Data collection and EPB event detection

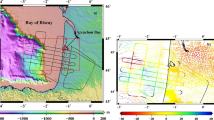
Figure 1 shows the experimental area and corresponding GNSS stations. Three stations CVMS, MAIR and PIGT are served as the reference stations and station MCTY is the user station, with geomagnetic latitudes 45.71, 47.07, 46.58 and 46.32, respectively. This area is in the southern U.S. and belongs to the middle latitudes. Compared to the low-latitudes, this area is not prone to the equatorial ionospheric anomaly, which is better to evaluate objectively the effects of EPB-induced ionospheric gradients. The 30-s sampling GNSS observation data (only including global positioning system (GPS)) were collected from the University NAVSTAR Consortium (UNAVCO) data center. The satellite DCB products were downloaded from the Center for Orbit Determination in Europe (CODE). Precise orbit and clock products related to PPP and PPP-RTK solutions were also collected in GeoForschungsZentrum (GFZ).

Fig. 1
figure 1

Locations of GNSS reference stations (blue triangles) and the user station (red dot) in the experiment. The average distance between the user station and the reference station is about 67 km

Full size image

The ionospheric slant TEC series (including satellite and receiver DCBs) for each satellite-receiver pair is estimated firstly using PPP technique. Then we employ them to detect EPB events. The results show an EPB event after sunset (19:56 LT) occurred on May 28, 2017. Figures 2 and 3 present the ionospheric slant TEC series observed by various satellites on May 28, 2017, at user station MCTY and reference station PIGT, respectively. Other two reference stations also observe similar results. Figure 4 further shows the locations of ionospheric pierce points for the ionospheric slant TEC observerd at station MCTY (other stations are very similar). As shown in the figures, significant TEC depletions occurred during 20:00–21:30 LT with depth (maximum depletion) of 10 ~ 20 TECU. The maximum depth is close to 20 TECU observed by satellite G29 at user station MCTY. So, big gradients are generated in ionosphere above this area. In addition, the data loss also occurred during this period (see the TEC series of satellite G05), which can be attributed to the ionospheric scintillation induced by the EPB.

Fig. 2
figure 2

Ionospheric slant TEC series (including satellite and receiver DCBs) observed by various satellites at user station MCTY on May 28, 2017. The solid lines are estimated values using PPP technique and the corresponding dashed lines are fitted background values. The TEC series of satellite G05 (red points) is a case for data loss. The vertical black dotted line indicates the sunset time (19:56 LT)

Full size image
Fig. 3
figure 3

Same as Fig. 2 but for the reference station PIGT

Full size image
Fig. 4
figure 4

The locations of ionospheric pierce points for ionospheric slant TEC oberved at station MCTY on May 28, 2017

Full size image

Our previous study has indicated the vertical depth of EPB varies from a few TECU to tens of TECU (Tang and Chen 2022). So, according to the magnitude, the detected EPB on May 28, 2017 can be considered as a common medium-scale event, which is representative. In the following parts, we will serve this event as a case to analyze the ionospheric gradients’ effects on PPP-RTK solutions.

Effects on the ionospheric residuals

By subtracting the observed TEC values from the fitted background TEC values (solid lines and dashed lines in Figs. 2 and 3, respectively), the TEC variations during EPB event are obtained. Then a reference satellite (take satellite G20 as an example here) is selected to compute the ionospheric residuals. Figure 5 plots the ionospheric residuals induced by EPB at user station MCTY. Shown here, the EPB-induced ionospheric residuals are large with maximum 8 TECU recorded by satellite pair G20–G29. As seen in Figs. 2 and 3, for the same satellite, the profiles of observed TEC depletions are similar at stations MCTY and PIGT. That is to say, even though both user station and reference stations observe TEC depletions, the residuals are still large and not canceled out. This can be attributed to the spatial and especially the temporal difference of TEC depletions between stations.

Fig. 5
figure 5

The ionospheric residual series induced by EPB at user station MCTY

Full size image

After correcting the satellite DCBs in ionospheric TEC series using the CODE products, the ionospheric residuals without EPB corrected and with EPB corrected at user station MCTY are calculated and plotted in Fig. 6, respectively. Here, the ionospheric residual with EPB corrected is obtained by subtracting the EPB-induced part from uncorrected ionospheric residuals. As shown in top panel, the maximum ionospheric residual is up to 7.5 TECU during the period of EPB event. Noted other relatively large residuals, especially during 21:30–22:30 LT are also existed with maximum about 2.5 TECU. These residuals can be attributed to other ionospheric irregularities: for example, wavelike disturbances are observable after 21:30 LT in Figs. 2 and 3. For period without obvious irregularities, such as the satellite pair G20–G02 during 19:00–20:00 LT, the residuals are generally less than 1 TECU. Here, we only focus on the EPB event and corresponding TEC depletions. So other ionospheric irregularities are not corrected. As shown in bottom panel, after correcting EPB, the ionospheric residuals during the period of EPB event reduce apparently to less than 1 TECU.

Fig. 6
figure 6

The ionospheric residual series without EPB correction (top panel) and with EPB correction (bottom panel) at user station MCTY

Full size image

Effects on the 3D positions

Above results show EPB-induced ionospheric gradients can dramatically increase the magnitude of ionospheric residuals. Now we assess the ionospheric residuals’ effects on the estimated 3D positions of PPP-RTK. Figure 7 plots the estimated errors in east (E), north (N) and up (U) directions at station MCTY without EPB correction (top panel) and with EPB correction (bottom panel) since 18:00 LT (00:00 UT), respectively. As shown in the figure, after initialization at data beginning, re-initialization occurs at 20:43 LT for both two modes. Data check reveals many satellite signals deteriorate and even lose lock (such as G05 plotted in Figs. 2 and 3) at this epoch. So, the cause of the re-initialization is attributed to the ionospheric scintillation. The corresponding PPP-RTK performances during the re-initialization process of the two modes are listed in Table 1. As presented in Fig. 1 and Table 1, for the mode without EPB correction (top panel), the convergence times are long especially in the E direction which is close to 2 h; the RMSs are large with several decimeters in all directions. For the mode with EPB correction (bottom panel), the re-initialization process is fast especially in the E and N directions with only several minutes; the RMSs are also significantly smaller than that of previous mode with centimeter-level in the E and N directions.

Fig. 7
figure 7

The 3D error series of PPP-RTK solution at station MCTY without EPB correction (top panel) and with EPB correction (bottom panel) calculated since 18:00 LT (00:00 UT)

Full size image
Table 1 The PPP-RTK performances during the re-initialization process. The calculation period of the root mean square (RMS) is 20:43–22:43 LT and the criterion of convergence is that the magnitude of error is below 0.1 m
Full size table

As presented in Fig. 7, the estimated 3D errors for two modes are basically consistent after the re-initialization process. Specially, they are also similar during 20:00–20:43 LT whether EPB is corrected or not. However, as shown in Fig. 5, the ionospheric residuals are large during this period. That is to say, if the PPP-RTK solutions of 3D positions are converged, the effects of EPB-induced ionospheric gradients are negligible. It is reasonable because the function of the ionospheric correction constraint is to reduce the convergence time of PPP-RTK solutions.

Above results show the EPB-induced ionospheric gradients mainly affect the initialization process. To further confirm that, the estimated 3D errors at station MCTY without EPB correction (top panel) and with EPB correction (bottom panel) since 20:30 LT are also calculated and plotted in Fig. 8. The corresponding PPP-RTK performances during the initialization process of the two modes are listed in Table 2. As shown in the figure and table, the convergence times are about 3 h in all directions and the RMSs of estimated errors are up to 1 ~ 2 m in N and U directions during initialization process without EPB correction. After correcting EPB, the corresponding convergence times and RMSs are reduced significantly. Compared to the initialization process (since 18:00 LT) in Fig. 7, the convergence times are still long in E and N directions with EPB correction. Obviously, the cause can be attributed to the ionospheric scintillation. In addition, similarly, the estimated 3D errors for two modes are basically consistent after the initialization process.

Fig. 8
figure 8

The 3D error series of PPP-RTK solution at station MCTY without EPB correction (top panel) and with EPB correction (bottom panel) calculated since 20:30 LT

Full size image
Table 2 The PPP-RTK performances during the initialization process. The calculation period of the root mean square (RMS) is 20:30–23:30 LT and the criterion of convergence is that the magnitude of error is below 0.1 m
Full size table

Conclusions

The EPB-induced ionospheric gradients can degrade the accuracy of ionospheric correction, thereby exerting impacts on the estimated results of GNSS PPP-RTK. To investigate its effects on GNSS PPP-RTK technique, data from four GNSS stations (three reference stations and one user station) located at southern U.S. and corresponding products are collected firstly. Then the EPB event occurred on May 28, 2017 is detected and served as a representative case. Finally, the ionospheric residuals and 3D positions of PPP-RTK solutions at user station are calculated using two modes, namely EPB uncorrected and corrected, respectively. The main results are presented as follows:

  1. 1.

    Although both user station and reference stations have observed TEC depletions, the interpolated ionospheric residuals at user station are still very large with maximum 7.5 TECU during the period of the EPB event. This can be attributed to the spatial and especially the temporal difference of TEC depletions between stations. After correcting EPB, the corresponding ionospheric residuals dramatically decrease to below 1 TECU.

  2. 2.

    If the EPB occurred during the initialization or re-initialization process of PPP-RTK solutions, the convergence times are very long and the RMSs of estimated errors are large, which can be about 3 h and 1 ~ 2 m for the initialization process. After correcting EPB, the corresponding convergence times and RMSs of estimated errors are reduced significantly. However, the effects are ignorable when the PPP-RTK solutions are converged.

In a word, the EPB-induced ionospheric gradients can dramatically amplify the magnitude of ionospheric residuals, and then significantly increase the estimated errors and lengthen the convergence times of 3D PPP-RTK solutions during initialization or re-initialization process. So, the effects of EPB-induced ionospheric gradients on PPP-RTK technique are non-ignorable. In this study, the EPB event is detected in post-processing. Research on detecting EPB in real-time to mitigate its effects is an important work in the future.