Multicriteria cuts and size-constrained k-cuts in hypergraphs

Abstract

We address counting and optimization variants of multicriteria global min-cut and size-constrained min-k-cut in hypergraphs.

• 1. For an r-rank n-vertex hypergraph endowed with t hyperedge-cost functions, we show that the number of multiobjective min-cuts is $O(r2^{tr}n^{3t-1})$. In particular, this shows that the number of parametric min-cuts in constant rank hypergraphs for a constant number of criteria is strongly polynomial, thus resolving an open question by Aissi et al. (Math Program 154(1–2):3–28, 2015). In addition, we give randomized algorithms to enumerate all multiobjective min-cuts and all pareto-optimal cuts in strongly polynomial-time.

• 2. We also address node-budgeted multiobjective min-cuts: For an n-vertex hypergraph endowed with t vertex-weight functions, we show that the number of node-budgeted multiobjective min-cuts is $O(r2^{r}n^{t+2})$, where r is the rank of the hypergraph, and the number of node-budgeted b-multiobjective min-cuts for a fixed budget-vector $b\in {\mathbb {R}}^t_{\ge 0}$ is $O(n^2)$.

• 3. We show that min-k-cut in hypergraphs subject to constant lower bounds on part sizes is solvable in polynomial-time for constant k, thus resolving an open problem posed by Guinez and Queyranne (Unpublished manuscript. . See also , 2012). Our technique also shows that the number of optimal solutions is polynomial.

All of our results build on the random contraction approach of Karger (Proceedings of the 4th annual ACM-SIAM symposium on discrete algorithms, SODA, pp 21–30, 1993). Our techniques illustrate the versatility of the random contraction approach to address counting and algorithmic problems concerning multiobjective min-cuts and size-constrained k-cuts in hypergraphs.

Appendix

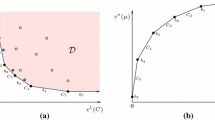
1.1 Comparison of parametric, pareto-optimal, and multiobjective cuts

We prove the containment relationship (1) here.

Proposition A.1

The following containment relationship holds, possibly with the containment being strict:

$$\begin{aligned} \text {Parametric min-cuts}&\subseteq \text {Pareto-optimal cuts} \subseteq \text {Multiobjective min-cuts}. \end{aligned}$$

Fig. 3

The cut $\delta (z)$ is a pareto-optimal cut but not a parametric min-cut

Proof

We first show that parametric min-cuts are pareto-optimal cuts: If a cut $F'$ dominates a cut F, then $w(F') < w(F)$ for all positive multipliers, and therefore F cannot be a parametric min-cut. On the other hand, not every pareto-optimal cut is a parametric min-cut (see Fig. 2 for an example).

Next, we show that pareto-optimal cuts are multiobjective min-cuts: If a cut F is pareto-optimal, then it is a b-multiobjective min-cut for the budget-vector b obtained by setting $b_i:=c_i(F)$ for every $i\in [k-1]$. On the other hand, not every multiobjective min-cut is a pareto-optimal cut (see Fig. 3 for an example). $\square$

Fig. 4

For $b=2$, the bold edge is a b-multiobjective min-cut but it is not a pareto-optimal cut

1.2 Proof of Lemma 1.1

We restate and prove Lemma 1.1.

Lemma 1.1

Let $r, \gamma , n$ be positive integers with $n\ge \gamma \ge r+1 > 2$. Let $f:{\mathbb {N}}\rightarrow {\mathbb {R}}_+$ be a positive-valued function defined over the natural numbers. Then, the optimum value of the linear program ($LP_1$) defined below is $\min _{2 \le j \le r } (1-\frac{j}{\gamma -r+j})f(n-j+1)$.

$$\begin{aligned}&\text {subject to} \quad&0 \le y_j \le x_j&\quad \forall j\in \{ 2,\ldots , r \} \end{aligned}$$

(2)

$$\begin{aligned}&\,&\sum _{j=2}^r x_j = 1&\end{aligned}$$

(3)

$$\begin{aligned}&\,&\gamma \sum _{j=2}^r y_j \le \sum _{j=2}^r j \cdot x_j&\end{aligned}$$

(4)

Proof

Setting $x_2=1$ and the rest of the variables to zero gives a feasible solution to the linear program (LP). Thus, the LP is feasible. Let $j \in \{2, \ldots , r\}$. Since $y_j \ge 0$ and $x_j \le 1$, we have that $x_j - y_j \le 1$. Since f is positive valued, we have that $f(n-j+1) \ge 0$ for every $j\in [2,r]$, so it follows that $(x_j-y_j)f(n-j+1) \le f(n-j+1)$. Therefore, we have $\sum _{j=2}^r (x_j-y_j)f(n-j+1) \le \sum _{j=2}^r f(n-j+1)$. Thus, the objective value of this LP is bounded. Since the LP is feasible and bounded, there exists an extreme point optimum solution to this LP. The LP has $2r-2$ variables and 2r equations, so every extreme point optimum will have at least $2r-2$ tight constraints and at most 2 non-tight constraints.

We now show that constraint (4) is tight for every optimal solution (x, y). Let (x, y) be an optimal solution. We first note that $x_j > 0$ for some $j \in \{2, \ldots , r\}$, by the third constraint. Therefore it is impossible that $y_j = 0$ for every $j \in \{2, \ldots , r\}$, since, if this were the case, we could choose some $j \in \{2, \ldots , r\}$ such that $x_j > 0$ and then increase $y_j$ by a small amount to improve the value of the objective function without violating any constraints, contradicting optimality. Now, since $\gamma \ge r+1$, we have

$$\begin{aligned} \gamma \sum _{j=2}^r y_j \ge \sum _{j=2}^r (r+1)y_j > \sum _{j=2}^r j \cdot y_j. \end{aligned}$$

This implies that we cannot have $y_j = x_j$ for all j, otherwise (x, y) would violate constraint (4). Hence, at least one of the $y_j \le x_j$ constraints must be slack. Let $j\in \{2, \ldots , r\}$ be such that $y_j<x_j$. If constraint (4) was slack, increasing the value of $y_j$ by a very small amount would improve the objective value of (x, y) without violating any constraints. Therefore, since (x, y) is optimal, constraint (4) must be tight.

Let (x, y) be an extreme point optimal solution. Since we know that $\sum _{j=2}^r x_j = 1$ and $x_j \ge 0$ for every $j \in \{2,\ldots ,r\}$, we have $\sum _{j=2}^r j \cdot x_j > 0$. Since constraint (4) is tight for (x, y), we must have $\gamma \sum _{j=2}^r y_j > 0$. This implies that there exists $j\in [2,r]$ such that $y_j>0$. Thus, we conclude that the two slack constraints must be $0 \le y_{j_1}$ and $y_{j_2} \le x_{j_2}$ for some $j_1, j_2\in \{2,\ldots , r\}$. We consider two cases.

• Case 1: Suppose $j_1 = j_2$. Then we have that $0< y_j < x_j = 1$ for some $j \in \{2,\ldots , r\}$, and $x_{j'},y_{j'}=0$ for every $j'\in \{2,\ldots , r\}{\setminus } \{j\}$. Therefore, we can simplify our LP to

  $$\begin{aligned} \begin{aligned}&\underset{y_j}{\text {minimize}}&(1-y_j)f(n-j+1) \\&\text {subject to}&0 \le y_j \le 1 \\&\gamma y_j = j. \end{aligned} \end{aligned}$$

  The only (and therefore optimal) solution to this LP is $y_j = \frac{j}{\gamma }$, which achieves an objective value of

  $$\begin{aligned} \left( 1-\frac{j}{\gamma }\right) f(n-j+1). \end{aligned}$$

• Case 2: Suppose $j_1 \ne j_2$. Then we have that $0 < y_{j_1} = x_{j_1}$, and $0 = y_{j_2} < x_{j_2}$. We note that $x_{j_2} = 1-x_{j_1}$, and therefore we can simplify the LP to

  $$\begin{aligned} \begin{aligned}&\underset{x_{j_1}}{\text {minimize}}&(1-x_{j_1})f(n-j_2+1) \\&\text {subject to}&0 \le x_{j_1} \le 1 \\&\gamma x_{j_1} = j_1 \cdot x_{j_1} + j_2 \cdot (1-x_{j_1}). \end{aligned} \end{aligned}$$

  Solving the second constraint for $x_{j_1}$ yields $x_{j_1} = \frac{j_2}{\gamma -j_1+j_2}$, and therefore our optimum value is

  $$\begin{aligned} \left( 1- \frac{j_2}{\gamma -j_1+j_2}\right) f(n-j_2+1). \end{aligned}$$

We conclude that the optimum value of the LP is equal to the minimum of the values from these two cases, that is,

$$\begin{aligned}&\min \left\{ \min _{j\in \{2,\ldots , r\}} \left\{ \left( 1-\frac{j}{\gamma }\right) f(n-j+1)\right\} , \, \, \,\right. \\&\left. \quad \min _{j_1,j_2 \in \{2,\ldots , r\}} \left\{ \left( 1- \frac{j_2}{\gamma -j_1+j_2})f(n-j_2+1)\right) \right\} \right\} . \end{aligned}$$

Since $(1- \frac{j_2}{\gamma -j_1+j_2})$ is decreasing in $j_1$ and $f(n-j_2+1)$ is always positive, we have

$$\begin{aligned}&\min _{j_1,j_2\in \{2,\ldots ,r\}} \left\{ \left( 1- \frac{j_2}{\gamma -j_1+j_2}\right) f(n-j_2+1)\right\} \\&\qquad = \min _{j\in \{2,\ldots , r\}} \left\{ \left( 1-\frac{j}{\gamma -r+j}\right) f(n-j+1)\right\} . \end{aligned}$$

Thus, since $j \le r$, the optimum value of the LP is equal to

$$\begin{aligned}&\min _{j\in \{2,\ldots , r\}}\left\{ \min \left\{ 1-\frac{j}{\gamma }, 1-\frac{j}{\gamma -r+j}\right\} f(n-j+1)\right\} \\&\qquad = \, \min _{j\in \{2,\ldots , r\}}\left\{ \left( 1-\frac{j}{\gamma -r+j}\right) f(n-j+1)\right\} . \end{aligned}$$

$\square$

1.3 Proof of Proposition 4.1

We restate and prove Proposition 4.1.

Proposition 4.1

For positive integers $n, e, \sigma$ with $e\ge 2$ and $n-e+1>2\sigma$, we have

$$\begin{aligned} \frac{{n-e \atopwithdelims ()\sigma }}{{n \atopwithdelims ()\sigma }} \cdot \frac{1}{{n-e+1 \atopwithdelims ()2\sigma }} \ge {n \atopwithdelims ()2\sigma }^{-1}. \end{aligned}$$

$\square$

Proof

We note that

$$\begin{aligned} \frac{{n-e \atopwithdelims ()\sigma }}{{n \atopwithdelims ()\sigma }} \cdot \frac{1}{{n-e+1 \atopwithdelims ()2\sigma }}&= \frac{(n-e)!(n-\sigma )!}{n!(n-e-\sigma )!} \cdot \frac{(2\sigma )!(n-e-2\sigma +1)!}{(n-e+1)!} \nonumber \\&= \left( \prod _{i=0}^{\sigma -1} \frac{n-e-i }{ n-i } \right) \cdot \frac{(2\sigma )!}{\prod _{i=0}^{2\sigma -1} (n-e+1-i)}. \end{aligned}$$

(17)

To lower bound this expression, we case on the value of e.

• Case 1: Suppose $e > \sigma$. Then we can lower bound expression (17) by

  $$\begin{aligned} \frac{1}{\prod _{i=0}^{\sigma -1} (n-i)} \cdot \frac{(2\sigma )!}{(n-e+1) \prod _{i=0}^{\sigma -2} (n-e-\sigma -i)} \ge&\frac{(2\sigma )!}{\prod _{i=0}^{2\sigma -1} (n-i)} = {n \atopwithdelims ()2\sigma }^{-1}\!. \end{aligned}$$

• Case 2: Suppose $e \le \sigma$. We note that

  $$\begin{aligned} \frac{(2\sigma )!}{\prod \limits _{i=0}^{2\sigma -1} (n-e+1-i)} = \frac{(2\sigma )!}{\prod \limits _{i=0}^{2\sigma -1} (n-i)} \cdot \prod _{i=0}^{e-2} \frac{n-i}{n-2\sigma -i} ={n \atopwithdelims ()2\sigma }^{-1} \cdot \prod _{i=0}^{e-2} \frac{n-i}{n-2\sigma -i}. \end{aligned}$$

  Thus, expression (17) is equal to

  $$\begin{aligned} {n \atopwithdelims ()2\sigma }^{-1} \cdot \left( \prod _{i=0}^{\sigma -1} \frac{n-e-i }{ n-i } \right) \left( \prod _{i=0}^{e-2} \frac{n-i}{n-2\sigma -i} \right) . \end{aligned}$$

  We will show that $\left( \prod _{i=0}^{\sigma -1} \frac{n-e-i }{ n-i } \right) \left( \prod _{i=0}^{e-2} \frac{n-i}{n-2\sigma -i} \right) \ge 1$. We note that

  $$\begin{aligned} \left( \prod _{i=0}^{\sigma -1} \frac{n-e-i }{ n-i } \right) \left( \prod _{i=0}^{e-2} \frac{n-i}{n-2\sigma -i} \right)&= \frac{\prod _{i=0}^{\sigma -1} (n-e-i) }{\prod _{i=e-1}^{\sigma -1} (n-i) } \cdot \frac{1 }{\prod _{i=0}^{e-2} (n-2\sigma -i) } \nonumber \\&= \frac{\prod _{i=\sigma }^{e+\sigma -1} (n-i) }{(n-e+1)\prod _{i=0}^{e-2} (n-2\sigma -i) }. \end{aligned}$$

  (18)

  We claim that expression (18) is minimized when $e = 2$. To see this, we note that

  $$\begin{aligned}&\frac{\prod _{i=\sigma }^{(e+1)+\sigma -1} (n-i) }{(n-(e+1)+1)\prod _{i=0}^{(e+1)-2} (n-2\sigma -i) }\\&\quad = \frac{\prod _{i=\sigma }^{e+\sigma -1} (n-i) }{(n-e+1)\prod _{i=0}^{e-2} (n-2\sigma -i) } \cdot \frac{(n-e-\sigma )(n-e+1) }{(n-2\sigma -e+1)(n-e)}. \end{aligned}$$

  Since $e \le \sigma$, we know that $n-e-\sigma \ge n-2\sigma +1$. From this, along with the fact that $n-e+1 > n-e$, we conclude that $\frac{(n-e-\sigma )(n-e+1) }{(n-2\sigma -e+1)(n-e)} > 1$. This means that expression (18) increases when we increment e. Thus

  $$\begin{aligned} \frac{\prod _{i=\sigma }^{e+\sigma -1} (n-i) }{(n-e+1)\prod _{i=0}^{e-2} (n-2\sigma -i) }\ge & {} \frac{(n-\sigma )(n-\sigma -1)}{(n-1)(n-2\sigma )}\\= & {} \frac{n^2 - (2\sigma +1)n + (\sigma +1)\sigma }{n^2 - (2\sigma +1)n +2\sigma } \ge 1. \end{aligned}$$

  The last inequality follows from the fact that $\sigma \ge 1$.

  Thus, we have shown that $\left( \prod _{i=0}^{\sigma -1} \frac{n-e-i }{ n-i } \right) \left( \prod _{i=0}^{e-2} \frac{n-i}{n-2\sigma -i} \right) \ge 1$, and therefore, combining the above inequalities, we have that

  $$\begin{aligned} \frac{{n-e \atopwithdelims ()\sigma }}{{n \atopwithdelims ()\sigma }} \cdot \frac{1}{{n-e+1 \atopwithdelims ()2\sigma }} \ge {n \atopwithdelims ()2\sigma }^{-1}. \end{aligned}$$

$\square$