Dynamic decision-making and coordination of low-carbon closed-loop supply chain considering different power structures and government double subsidy

Abstract

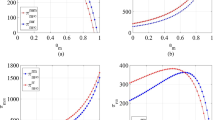
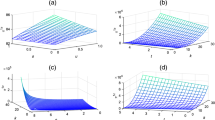
Low-carbon closed-loop supply chain (LC-CLSC) plays an important role in realizing a low-carbon circular economy. In order to facilitate governments to make emission reduction subsidy and recycling subsidy decisions and LC-CLSC members to formulate pricing, emission reduction investment and recycling investment decisions, this paper proposes multiple three-level differential game models of a LC-CLSC involving the manufacturer, retailer and government considering the dynamic characteristics of product goodwill and recycling rate. Under the four scenarios of three different power structures: manufacturer-led, retailer-led and non-led, and centralized decision-making, some critical equilibrium results are first solved and discussed, including government’s optimal emission reduction subsidy and recycling subsidy rates, the manufacturer’s wholesale price and emission reduction investment, the retailer’s retail price and recycling investment, product goodwill and waste product recycling rate, profits of the manufacturer, retailer and government, etc. To further achieve the LC-CLSC coordination, the contracts under three different power structures are designed, and the conditions that the coordination parameters satisfy are given. Through mathematical derivation of equilibrium results and sensitivity analysis with the help of numerical examples, this paper finds that the government subsidy rates are dependent on the power status between manufacturers and retailers, and the weaker party will get higher subsidy rate. The government subsidy mechanism can significantly reduce the gaps between the manufacturer-led and retailer-led cases, such as manufacturer’s emission reduction investment, the retailer’s recycling investment, steady-state retail price, and product goodwill and recycling rate. Under the effect of the government subsidy mechanism, the non-led case is more conducive to the recycling of waste products and the improvement of social welfare than the unilateral domination cases. The findings can help manufacturers and retailers in the LC-CLSC formulate optimal strategies like pricing, emission reduction and recycling, and develop coordination contracts to further improve the overall performance of the supply chain according to their different power structures. More importantly, they can also help governments make optimal emission reduction and recycling subsidy decisions according to member companies’ different power structures so as to improve subsidy efficiency.

Graphical abstract

Appendices

Appendix 4.1

Theorem 1

(1) The optimal decisions of the manufacturer and retailer are as follows:

$$\left\{ \begin{gathered} w^{m} = \frac{{\left[ {\alpha + \left( {\mu + 2\beta b - \beta c - \beta \Delta } \right)\varepsilon } \right]\sqrt {G^{m} \left( t \right)} }}{2\beta } \hfill \\ E^{m} = \frac{{\phi \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{8\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{m}^{m} } \right)\eta_{m} }} \hfill \\ \end{gathered} \right.,\;\left\{ \begin{gathered} p^{m} = \frac{{\left[ {3\alpha + \left( {3\mu + \beta c - \beta \Delta } \right)\varepsilon } \right]\sqrt {G^{m} \left( t \right)} }}{4\beta } \hfill \\ A^{m} = \frac{{\lambda \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{16\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{r}^{m} } \right)\eta_{r} }} \hfill \\ \end{gathered} \right.$$

(2) The optimal emission reduction and recycling subsidy rates set by the government are as follows:

$$\theta_{m}^{m} = \frac{3}{7},\;\theta_{r}^{m} = \frac{5}{7}$$

(3) The optimal evolution trajectories of product goodwill and waste product recycling rate are, respectively, as follows:

$$G^{m} \left( t \right) = \left( {G_{0} - G_{\infty }^{m} } \right)e^{ - \sigma t} + G_{\infty }^{m}$$

$$\tau^{m} \left( t \right) = \varepsilon \sqrt {G^{m} \left( t \right)} = \varepsilon \sqrt {\left( {G_{0} - G_{\infty }^{m} } \right)e^{ - \sigma t} + G_{\infty }^{m} }$$

(4) The optimal profits of the manufacturer and retailer are as follows:

$$\pi_{m}^{m} \left( t \right) = \pi_{m\infty }^{m} + a_{1} \left( {G_{0} - G_{\infty }^{m} } \right)e^{ - \sigma t} ,\;\pi_{r}^{m} \left( t \right) = \pi_{r\infty }^{m} + a_{2} \left( {G_{0} - G_{\infty }^{m} } \right)e^{ - \sigma t}$$

(5) The government’s optimal income is as follows:

$$\pi_{g}^{m} \left( t \right) = \pi_{g\infty }^{m} + a_{3} \left( {G_{0} - G_{\infty }^{m} } \right)e^{ - \sigma t}$$

Theorem 2

(1) when $t \to \infty$,the steady-state product goodwill and waste product recycling rate are, respectively, as follows:

$$G_{\infty }^{m} = \frac{{7\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{32\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right),\;\tau_{\infty }^{m} = \varepsilon \sqrt {G_{\infty }^{m} } = \varepsilon \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]\sqrt {\frac{7}{{32\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)}$$

(2) when $t \to \infty$, the steady-state product wholesale price and retail price are, respectively, as follows:

$$\begin{gathered} w_{\infty }^{m} = \frac{{\left[ {\alpha + \left( {\mu + 2\beta b - \beta c - \beta \Delta } \right)\varepsilon } \right]\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]}}{2\beta }\sqrt {\frac{7}{{32\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)} ,\; \hfill \\ p_{\infty }^{m} = \frac{{\left[ {3\alpha + \left( {3\mu + \beta c - \beta \Delta } \right)\varepsilon } \right]\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]}}{4\beta }\sqrt {\frac{7}{{32\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)} \hfill \\ \end{gathered}$$

(3) when $t \to \infty$, the steady-state profits of the manufacturer and retailer are, respectively, as follows:

$$\pi_{m\infty }^{m} = a_{1} G_{\infty }^{m} + d_{1} ,\;\pi_{r\infty }^{m} = a_{2} G_{\infty }^{m} + d_{2}$$

where $a_{1} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{8\beta \left( {\rho + \sigma } \right)}}$,$a_{2} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{16\beta \left( {\rho + \sigma } \right)}}$,$d_{1} = \frac{1}{\rho }\left[ {\frac{{7\phi^{2} \left( {a_{1} } \right)^{2} }}{{8\eta_{m} }} + \frac{{7\lambda^{2} a_{1} a_{2} }}{{2\eta_{r} }}} \right]$,

$$d_{2} = \frac{1}{\rho }\left[ {\frac{{7\lambda^{2} \left( {a_{2} } \right)^{2} }}{{4\eta_{r} }} + \frac{{7\phi^{2} a_{1} a_{2} }}{{4\eta_{m} }}} \right]$$

(4) when $t \to \infty$, the steady-state income of the government is as follows:

$$\pi_{g\infty }^{m} = a_{3} G_{\infty }^{m} + d_{3}$$

where $a_{3} = \frac{{7\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{32\beta \left( {\rho + \sigma } \right)}}$,$d_{3} = \frac{{\left( {a_{3} } \right)^{2} }}{2\rho }\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)$ The proof of Theorem 1 is similar to the proof of Theorem 3 and is omitted.

Appendix 4.2

Theorem 3

(1) The optimal decisions of the manufacturer and retailer are as follows:

$$\left\{ \begin{gathered} w^{r} = \frac{{\left[ {\alpha + \left( {\mu + 4\beta b - \beta c - 3\beta \Delta } \right)\varepsilon } \right]\sqrt {G^{r} \left( t \right)} }}{4\beta } \hfill \\ E^{r} = \frac{{\phi \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{16\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }} \hfill \\ \end{gathered} \right.,\;\left\{ \begin{gathered} p^{r} = \frac{{\left[ {3\alpha + \left( {3\mu + \beta c - \beta \Delta } \right)\varepsilon } \right]\sqrt {G^{r} \left( t \right)} }}{4\beta } \hfill \\ A^{r} = \frac{{\lambda \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{8\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{r}^{r} } \right)\eta_{r} }} \hfill \\ \end{gathered} \right.$$

(2) The optimal emission reduction and recycling subsidy rates set by the government are as follows:

$$\theta_{m}^{r} = \frac{5}{7},\;\theta_{r}^{r} = \frac{3}{7}$$

(3) The optimal evolution trajectories of product goodwill and waste product recycling rate are, respectively, as follows:

$$G^{r} \left( t \right) = \left( {G_{0} - G_{\infty }^{r} } \right)e^{ - \sigma t} + G_{\infty }^{r}$$

$$\tau^{r} \left( t \right) = \varepsilon \sqrt {G^{r} \left( t \right)} = \varepsilon \sqrt {\left( {G_{0} - G_{\infty }^{r} } \right)e^{ - \sigma t} + G_{\infty }^{r} }$$

(4) The optimal profits of the manufacturer and retailer are as follows:

$$\pi_{m}^{r} \left( t \right) = \pi_{m\infty }^{r} + a_{4} \left( {G_{0} - G_{\infty }^{r} } \right)e^{ - \sigma t} ,\;\pi_{r}^{r} \left( t \right) = \pi_{r\infty }^{r} + a_{5} \left( {G_{0} - G_{\infty }^{r} } \right)e^{ - \sigma t}$$

(5) The government’s optimal income is as follows:

$$\pi_{g}^{r} \left( t \right) = \pi_{g\infty }^{r} + a_{6} \left( {G_{0} - G_{\infty }^{r} } \right)e^{ - \sigma t}$$

Theorem 4

(1) when $t \to \infty$, the steady-state product goodwill and waste product recycling rate are, respectively, as follows:

$$\begin{gathered} G_{\infty }^{r} = \frac{{7\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{32\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right), \hfill \\ \tau_{\infty }^{r} = \varepsilon \sqrt {G_{\infty }^{r} } = \varepsilon \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]\sqrt {\frac{7}{{32\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)} \hfill \\ \end{gathered}$$

(2) when $t \to \infty$, the steady-state product wholesale price and retail price are, respectively, as follows:

$$\begin{gathered} w_{\infty }^{r} = \frac{{\left[ {\alpha + \left( {\mu + 4\beta b - \beta c - 3\beta \Delta } \right)\varepsilon } \right]\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]}}{4\beta }\sqrt {\frac{7}{{32\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)} , \hfill \\ p_{\infty }^{r} = \frac{{\left[ {3\alpha + \left( {3\mu + \beta c - \beta \Delta } \right)\varepsilon } \right]\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]}}{4\beta }\sqrt {\frac{7}{{32\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)} \hfill \\ \end{gathered}$$

(3) when $t \to \infty$, the steady-state profits of the manufacturer and retailer are, respectively, as follows:

$$\pi_{m\infty }^{r} = a_{4} G_{\infty }^{r} + d_{4} ,\;\pi_{r\infty }^{r} = a_{5} G_{\infty }^{r} + d_{5}$$

where

$$\begin{gathered} a_{4} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{16\beta \left( {\rho + \sigma } \right)}},\;a_{5} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{8\beta \left( {\rho + \sigma } \right)}} \hfill \\ d_{4} = \frac{1}{\rho }\left[ {\frac{{7\phi^{2} \left( {a_{4} } \right)^{2} }}{{4\eta_{m} }} + \frac{{7\lambda^{2} a_{4} a_{5} }}{{4\eta_{r} }}} \right],\;d_{5} = \frac{1}{\rho }\left[ {\frac{{7\lambda^{2} \left( {a_{5} } \right)^{2} }}{{8\eta_{r} }} + \frac{{7\phi^{2} a_{4} a_{5} }}{{2\eta_{m} }}} \right] \hfill \\ \end{gathered}$$

(4) when $t \to \infty$, the steady-state income of the government is as follows:

$$\pi_{g\infty }^{r} = a_{6} G_{\infty }^{r} + d_{6}$$

where

$$a_{6} = \frac{{7\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{32\beta \left( {\rho + \sigma } \right)}},\;d_{6} = \frac{{\left( {a_{6} } \right)^{2} }}{2\rho }\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)$$

Proof of Theorem 3

According to Eq. (5), we first let $\pi_{m}^{r} \left( G \right) = e^{ - \rho t} V_{m}^{r} \left( G \right)$, and then based on the optimal control theory,$V_{m}^{r} \left( G \right)$ for any $G \ge 0$, the following HJB equation is satisfied:

$$\rho V_{m}^{r} \left( G \right) = \mathop {\max }\limits_{w,E} \left\{ {\left[ {w + \left( {\Delta - b} \right)\varepsilon \sqrt G } \right]\left[ {\left( {\alpha + \mu \varepsilon } \right)\sqrt G - \beta p} \right] - \frac{{\left( {1 - \theta_{m}^{r} } \right)\eta_{m} E^{2} }}{2} + \frac{{\partial V_{m}^{r} }}{\partial G}\left( {\phi E + \lambda A - \sigma G} \right)} \right\}$$

Let $p = w + m$, by solving the first-order partial derivative of $w$ and $E$, and the optimal first-order condition, we can get:

$$w^{r} = \frac{{\left[ {\alpha + \left( {\mu + \beta b - \beta \Delta } \right)\varepsilon } \right]\sqrt G - \beta m}}{2\beta },\;E^{r} = \frac{{\phi \frac{{\partial V_{m}^{r} }}{\partial G}}}{{\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }}$$

Then according to Eq. (6), let $\pi_{r}^{r} \left( G \right) = e^{ - \rho t} V_{r}^{r} \left( G \right)$, and then based on the optimal control theory,$V_{r}^{r} \left( G \right)$ for any $G \ge 0$, the following HJB equation is satisfied:

$$\begin{gathered} \rho V_{r}^{r} \left( G \right) = \mathop {\max }\limits_{p,A} \left\{ {\left[ {\left( {p - w} \right) + \left( {b - c} \right)\varepsilon \sqrt G } \right]\left[ {\left( {\alpha + \mu \varepsilon } \right)\sqrt G - \beta p} \right] - \frac{{\left( {1 - \theta_{r}^{r} } \right)\eta_{r} A^{2} }}{2} + \frac{{\partial V_{r}^{r} }}{\partial G}\left( {\phi E + \lambda A - \sigma G} \right)} \right\} \hfill \\ = \mathop {\max }\limits_{p,A} \left\{ {\left[ {m + \left( {b - c} \right)\varepsilon \sqrt G } \right]\left[ {\frac{{\left[ {\alpha + \left( {\mu - \beta b + \beta \Delta } \right)\varepsilon } \right]\sqrt G - \beta m}}{2}} \right] - \frac{{\left( {1 - \theta_{r}^{r} } \right)\eta_{r} A^{2} }}{2} + \frac{{\partial V_{r}^{r} }}{\partial G}\left( {\phi \frac{{\phi \frac{{\partial V_{m}^{r} }}{\partial G}}}{{\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }} + \lambda A - \sigma G} \right)} \right\} \hfill \\ \end{gathered}$$

By solving the first-order partial derivative of $m$ and $A$, and the optimal first-order condition, we can get:

$$m = \frac{{\left[ {\alpha + \left( {\mu - 2\beta b + \beta c + \beta \Delta } \right)\varepsilon } \right]\sqrt G }}{2\beta },\;A^{r} = \frac{{\lambda \frac{{\partial V_{r}^{r} }}{\partial G}}}{{\left( {1 - \theta_{r}^{r} } \right)\eta_{r} }}$$

Then, we can get the optimal wholesale price and retail price are as follows:

$$w^{r} = \frac{{\left[ {\alpha + \left( {\mu + 4\beta b - \beta c - 3\beta \Delta } \right)\varepsilon } \right]\sqrt G }}{4\beta },\;p^{r} = \frac{{\left[ {3\alpha + \left( {3\mu + \beta c - \beta \Delta } \right)\varepsilon } \right]\sqrt G }}{4\beta }$$

Then, substituting the above equilibrium solutions into the HJB equations of the manufacturer’s and retailer’s objective functions, and further sorting it out, we can get:

$$\begin{gathered} \rho V_{r}^{r} \left( G \right) = \left\{ {\frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{8\beta } - \sigma \frac{{\partial V_{r}^{r} }}{\partial G}} \right\}G + \frac{{\lambda^{2} \left( {\frac{{\partial V_{r}^{r} }}{\partial G}} \right)^{2} }}{{2\left( {1 - \theta_{r}^{r} } \right)\eta_{r} }} + \frac{{\phi^{2} \frac{{\partial V_{r}^{r} }}{\partial G}\frac{{\partial V_{m}^{r} }}{\partial G}}}{{\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }} \hfill \\ \rho V_{m}^{r} \left( G \right) = \left\{ {\frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{16\beta } - \sigma \frac{{\partial V_{m}^{r} }}{\partial G}} \right\}G + \frac{{\phi^{2} \left( {\frac{{\partial V_{m}^{r} }}{\partial G}} \right)^{2} }}{{2\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }} + \frac{{\lambda^{2} \frac{{\partial V_{m}^{r} }}{\partial G}\frac{{\partial V_{r}^{r} }}{\partial G}}}{{\left( {1 - \theta_{r}^{r} } \right)\eta_{r} }} \hfill \\ \end{gathered}$$

According to the structural characteristics of the above expression, we assume that $V_{m}^{r} \left( G \right)$ and $V_{r}^{r} \left( G \right)$ satisfy the following expression, respectively:

$$\begin{gathered} V_{m}^{r} \left( G \right) = a_{4} G + d_{4} \hfill \\ V_{r}^{r} \left( G \right) = a_{5} G + d_{5} \hfill \\ \end{gathered}$$

where $a_{4}$,$d_{4}$,$a_{5}$ and $d_{5}$ are all constants.

Then, we can get:

$$\left\{ \begin{gathered} \rho a_{4} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{16\beta } - \sigma a_{4} \hfill \\ \rho d_{4} = \frac{{\phi^{2} \left( {a_{4} } \right)^{2} }}{{2\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }} + \frac{{\lambda^{2} a_{4} a_{5} }}{{\left( {1 - \theta_{r}^{r} } \right)\eta_{r} }} \hfill \\ \rho a_{5} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{8\beta } - \sigma a_{5} \hfill \\ \rho d_{5} = \frac{{\lambda^{2} \left( {a_{5} } \right)^{2} }}{{2\left( {1 - \theta_{r}^{r} } \right)\eta_{r} }} + \frac{{\phi^{2} a_{4} a_{5} }}{{\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }} \hfill \\ \end{gathered} \right.$$

By solving the equations, we can obtain:

$$\begin{gathered} a_{4} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{16\beta \left( {\rho + \sigma } \right)}},\;a_{5} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{8\beta \left( {\rho + \sigma } \right)}} \hfill \\ d_{4} = \frac{1}{\rho }\left[ {\frac{{\phi^{2} \left( {a_{4} } \right)^{2} }}{{2\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }} + \frac{{\lambda^{2} a_{4} a_{5} }}{{\left( {1 - \theta_{r}^{r} } \right)\eta_{r} }}} \right],\;d_{5} = \frac{1}{\rho }\left[ {\frac{{\lambda^{2} \left( {a_{5} } \right)^{2} }}{{2\left( {1 - \theta_{r}^{r} } \right)\eta_{r} }} + \frac{{\phi^{2} a_{4} a_{5} }}{{\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }}} \right] \hfill \\ \end{gathered}$$

Then substituting the above results into the expressions of the manufacturer’s optimal emission reduction investment strategy and the retailer’s optimal recycling investment strategy, the manufacturer’s optimal emission reduction investment decision and the retailer’s optimal recycling investment decision can be obtained as follows:

$$\left\{ \begin{gathered} E^{r} = \frac{{\phi \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{16\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{m}^{r} } \right)\eta_{m} }} \hfill \\ A^{r} = \frac{{\lambda \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{8\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{r}^{r} } \right)\eta_{r} }} \hfill \\ \end{gathered} \right.$$

Finally, we will solve the government’s optimal control problem. According to Eq. (8), we first let $\pi_{g}^{r} \left( G \right) = e^{ - \rho t} V_{g}^{r} \left( G \right)$, and then based on the optimal control theory,$V_{g}^{r} \left( G \right)$ for any $G \ge 0$, the following HJB equation is satisfied:

$$\rho V_{g}^{r} \left( G \right) = \mathop {\max }\limits_{{\theta_{m}^{r} ,\theta_{r}^{r} }} \left\{ {\left[ {p + \left( {\Delta - c} \right)\varepsilon \sqrt G } \right]\left[ {\left( {\alpha + \mu \varepsilon } \right)\sqrt G - \beta p} \right] - \frac{{\eta_{m} E^{2} }}{2} - \frac{{\eta_{r} A^{2} }}{2} + \frac{{\partial V_{g}^{r} }}{\partial G}\left( {\phi E + \lambda A - \sigma G} \right)} \right\}$$

By solving the first-order partial derivative of $\theta_{m}^{r}$ and $\theta_{r}^{r}$, and the optimal first-order condition, we can get:

$$\theta_{m}^{r} = 1 - \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{16\beta \left( {\rho + \sigma } \right)\frac{{\partial V_{g}^{r} }}{\partial G}}},\;\theta_{r}^{r} = 1 - \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{8\beta \left( {\rho + \sigma } \right)\frac{{\partial V_{g}^{r} }}{\partial G}}}$$

Substituting the above-mentioned government’s optimal feedback strategies back to the HJB equation, and further sorting it out, we can get:

$$\rho V_{g}^{r} \left( G \right) = \left\{ {\frac{{3\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{16\beta } - \sigma \frac{{\partial V_{g}^{r} }}{\partial G}} \right\}G + \frac{{\phi^{2} \left( {\frac{{\partial V_{g}^{r} }}{\partial G}} \right)^{2} }}{{2\eta_{m} }} + \frac{{\lambda^{2} \left( {\frac{{\partial V_{g}^{r} }}{\partial G}} \right)^{2} }}{{2\eta_{r} }}$$

According to the structural characteristics of the above expression, we assume that $V_{g}^{r} \left( G \right)$ satisfies the following expression:

$$V_{g}^{r} \left( G \right) = a_{6} G + d_{6}$$

where $a_{6}$ and $d_{6}$ are all constants.

Then, we can get:

$$\left\{ \begin{gathered} \rho a_{6} = \frac{{3\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{16\beta } - \sigma a_{6} \hfill \\ \rho d_{6} = \frac{{\phi^{2} \left( {\frac{{\partial V_{g}^{r} }}{\partial G}} \right)^{2} }}{{2\eta_{m} }} + \frac{{\lambda^{2} \left( {\frac{{\partial V_{g}^{r} }}{\partial G}} \right)^{2} }}{{2\eta_{r} }} \hfill \\ \end{gathered} \right.$$

By solving the equations, we can obtain:

$$a_{6} = \frac{{3\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{16\beta \left( {\rho + \sigma } \right)}},\;d_{6} = \frac{1}{\rho }\left[ {\frac{{\phi^{2} \left( {a_{6} } \right)^{2} }}{{2\eta_{m} }} + \frac{{\lambda^{2} \left( {a_{6} } \right)^{2} }}{{2\eta_{r} }}} \right]$$

Then substituting the above results into the expression of the government's optimal emission reduction and recovery subsidy strategy, we can get: $\theta_{r}^{r} = \frac{3}{7}$,$\theta_{m}^{r} = \frac{5}{7}$.

Theorem 3 is proved.

Appendix 4.3

Theorem 5

(1) The optimal decisions of the manufacturer and retailer are as follows:

$$\left\{ \begin{gathered} w^{n} = \frac{{\left[ {\alpha + \left( {\mu + 3\beta b - \beta c - 2\beta \Delta } \right)\varepsilon } \right]\sqrt {G^{n} \left( t \right)} }}{3\beta } \hfill \\ E^{n} = \frac{{\phi \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{9\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{m}^{n} } \right)\eta_{m} }} \hfill \\ \end{gathered} \right.,\;\left\{ \begin{gathered} p^{n} = \frac{{\left[ {2\alpha + \left( {2\mu + \beta c - \beta \Delta } \right)\varepsilon } \right]\sqrt {G^{n} \left( t \right)} }}{3\beta } \hfill \\ A^{n} = \frac{{\lambda \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{9\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{r}^{n} } \right)\eta_{r} }} \hfill \\ \end{gathered} \right.$$

(2) The optimal emission reduction and recycling subsidy rates set by the government are as follows:

$$\theta_{m}^{n} = \frac{3}{5},\;\theta_{r}^{n} = \frac{3}{5}$$

(3) The optimal evolution trajectories of product goodwill and waste product recycling rate are, respectively, as follows:

$$G^{n} \left( t \right) = \left( {G_{0} - G_{\infty }^{n} } \right)e^{ - \sigma t} + G_{\infty }^{n}$$

$$\tau^{n} \left( t \right) = \varepsilon \sqrt {G^{n} \left( t \right)} = \varepsilon \sqrt {\left( {G_{0} - G_{\infty }^{n} } \right)e^{ - \sigma t} + G_{\infty }^{n} }$$

(4) The optimal profits of the manufacturer and retailer are as follows:

$$\pi_{m}^{n} \left( t \right) = \pi_{m\infty }^{n} + a_{7} \left( {G_{0} - G_{\infty }^{n} } \right)e^{ - \sigma t} ,\;\pi_{r}^{n} \left( t \right) = \pi_{r\infty }^{n} + a_{8} \left( {G_{0} - G_{\infty }^{n} } \right)e^{ - \sigma t}$$

(5) The government’s optimal income is as follows:

$$\pi_{g}^{n} \left( t \right) = \pi_{g\infty }^{n} + a_{9} \left( {G_{0} - G_{\infty }^{n} } \right)e^{ - \sigma t}$$

Theorem 6

(1) when $t \to \infty$,the steady-state product goodwill and waste product recycling rate are, respectively, as follows:

$$G_{\infty }^{n} = \frac{{5\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{18\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right),\;\tau_{\infty }^{n} = \varepsilon \sqrt {G_{\infty }^{n} } = \varepsilon \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]\sqrt {\frac{5}{{18\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)}$$

(2) when $t \to \infty$, the steady-state product wholesale price and retail price are, respectively, as follows:

$$\begin{gathered} w_{\infty }^{n} = \frac{{\left[ {\alpha + \left( {\mu + 3\beta b - \beta c - 2\beta \Delta } \right)\varepsilon } \right]\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]}}{3\beta }\sqrt {\frac{5}{{18\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)} ,\; \hfill \\ p_{\infty }^{n} = \frac{{\left[ {2\alpha + \left( {2\mu + \beta c - \beta \Delta } \right)\varepsilon } \right]\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]}}{3\beta }\sqrt {\frac{5}{{18\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)} \hfill \\ \end{gathered}$$

(3) when $t \to \infty$,the steady-state profits of the manufacturer and retailer are, respectively, as follows:

$$\pi_{m\infty }^{n} = a_{7} G_{\infty }^{n} + d_{7} ,\;\pi_{r\infty }^{n} = a_{8} G_{\infty }^{n} + d_{8}$$

where

$$\begin{gathered} a_{7} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{9\beta \left( {\rho + \sigma } \right)}},\;a_{8} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{9\beta \left( {\rho + \sigma } \right)}}, \hfill \\ d_{7} = \frac{1}{\rho }\left[ {\frac{{5\phi^{2} \left( {a_{7} } \right)^{2} }}{{4\eta_{m} }} + \frac{{5\lambda^{2} a_{7} a_{8} }}{{2\eta_{r} }}} \right],\;d_{8} = \frac{1}{\rho }\left[ {\frac{{5\lambda^{2} \left( {a_{8} } \right)^{2} }}{{4\eta_{r} }} + \frac{{5\phi^{2} a_{7} a_{8} }}{{2\eta_{m} }}} \right] \hfill \\ \end{gathered}$$

(4) when $t \to \infty$,the steady-state income of the government is as follows:

$$\pi_{g\infty }^{n} = a_{9} G_{\infty }^{n} + d_{9}$$

where

$$a_{9} = \frac{{5\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{18\beta \left( {\rho + \sigma } \right)}},\;d_{9} = \frac{{\left( {a_{9} } \right)^{2} }}{2\rho }\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)$$

The proof of Theorem 5 is similar to the proof of Theorem 3 and is omitted.

Appendix 4.4

Theorem 7

(1) The optimal decisions of the LC-CLSC are as follows:

$$\left\{ \begin{gathered} p^{c} = \frac{{\left[ {\alpha + \left( {\mu + \beta c - \beta \Delta } \right)\varepsilon } \right]\sqrt {G^{c} \left( t \right)} }}{2\beta } \hfill \\ E^{c} = \frac{{\phi \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{4\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{m}^{c} } \right)\eta_{m} }} \hfill \\ A^{c} = \frac{{\lambda \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{4\beta \left( {\rho + \sigma } \right)\left( {1 - \theta_{r}^{c} } \right)\eta_{r} }} \hfill \\ \end{gathered} \right.$$

(2) The optimal emission reduction and recycling subsidy rates set by the government are as follows:

$$\theta_{m}^{c} = \frac{1}{3},\;\theta_{r}^{c} = \frac{1}{3}$$

(3) The optimal evolution trajectories of product goodwill and waste product recycling rate are, respectively, as follows:

$$G^{c} \left( t \right) = \left( {G_{0} - G_{\infty }^{c} } \right)e^{ - \sigma t} + G_{\infty }^{c}$$

$$\tau^{c} \left( t \right) = \varepsilon \sqrt {G^{c} \left( t \right)} = \varepsilon \sqrt {\left( {G_{0} - G_{\infty }^{c} } \right)e^{ - \sigma t} + G_{\infty }^{c} }$$

(4) The optimal profit of the LC-CLSC is as follows:

$$\pi_{sc}^{c} \left( t \right) = \pi_{sc\infty }^{c} + a_{10} \left( {G_{0} - G_{\infty }^{c} } \right)e^{ - \sigma t}$$

(5) The government’s optimal income is as follows:

$$\pi_{g}^{c} \left( t \right) = \pi_{g\infty }^{c} + a_{11} \left( {G_{0} - G_{\infty }^{c} } \right)e^{ - \sigma t}$$

Theorem 8

(1) when $t \to \infty$,the steady-state product goodwill and waste product recycling rate are, respectively, as follows:

$$\begin{gathered} G_{\infty }^{c} = \frac{{3\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{8\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right),\; \hfill \\ \tau_{\infty }^{c} = \varepsilon \sqrt {G_{\infty }^{c} } = \varepsilon \left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]\sqrt {\frac{3}{{8\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)} \hfill \\ \end{gathered}$$

(2) when $t \to \infty$, the steady-state product retail price is as follows:

$$p_{\infty }^{c} = \frac{{\left[ {\alpha + \left( {\mu + \beta c - \beta \Delta } \right)\varepsilon } \right]\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]}}{2\beta }\sqrt {\frac{3}{{8\beta \sigma \left( {\rho + \sigma } \right)}}\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)}$$

(3) when $t \to \infty$, the steady-state profit of the LC-CLSC is as follows:

$$\pi_{sc\infty }^{c} = a_{10} G_{\infty }^{c} + d_{10}$$

where $a_{10} = \frac{{\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{4\beta \left( {\rho + \sigma } \right)}},\;d_{10} = \frac{{3\left( {a_{10} } \right)^{2} }}{4\rho }\left[ {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right]$(4) when $t \to \infty$, the steady-state income of the government is as follows:

$$\pi_{g\infty }^{c} = a_{11} G_{\infty }^{c} + d_{11}$$

where $a_{11} = \frac{{3\left[ {\alpha + \left( {\mu - \beta c + \beta \Delta } \right)\varepsilon } \right]^{2} }}{{8\beta \left( {\rho + \sigma } \right)}},\;d_{11} = \frac{{\left( {a_{11} } \right)^{2} }}{2\rho }\left( {\frac{{\phi^{2} }}{{\eta_{m} }} + \frac{{\lambda^{2} }}{{\eta_{r} }}} \right)$The proof of Theorem 7 is similar to the proof of Theorem 3 and is omitted.