Dynamic responses of TLP considering coupled transverse and axial effect of tether under second-order wave and freak wave

Abstract

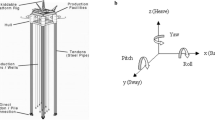
The objective of this paper is to analyze the dynamic responses of Tension Leg Platform (TLP). Under the combined action of waves and currents, a tether model considering the coupled effects of transverse and axial responses is established. The finite difference method is used in the numerical algorithm of the tether vibration model. Three simulations are performed, including a first-order irregular wave, a second-order wave, and a freak wave impact against the platform. The dynamic response characteristics of the tension leg platform under the action of freak waves are calculated by using the superposition model to generate the time history of freak waves. The numerical simulation results show that the platform motions are significantly affected by the freak waves, especially in the focusing location. And the effects of second-order wave force and freak wave force on the platform responses, horizontal offset, and vertical subsidence are analyzed.

Appendices

Appendix A: the platform hydrodynamic coefficients

Under the action of waves, the platform hydrodynamic coefficients are determined by BEM. Since the platform is a slender structure, the effect of wave viscous on the slender structure cannot be ignored. Then, the drag force on floating structure is determined by Morison equation. Therefore, hydrodynamic coefficient of the platform is calculated by the methods of BEM and Morison equation.

1.1 Added mass and memory function

The added mass and memory function can be determined by calculating the radiation potential of the platform. The integral equation of the radiation potential is calculated by using the boundary element method. The expression [25, 26] is shown as follows:

$$\begin{gathered} \hfill 2\pi \Phi_{k} (p,t) + \iint\limits_{{s_{b} }} {\left[ \begin{gathered} \Phi_{k} (q,t)\frac{\partial }{{\partial n_{q} }}\left( {\frac{1}{r} - \frac{1}{{r^{\prime}}}} \right) \hfill \\ - \left( {\frac{1}{r} - \frac{1}{{r^{\prime}}}} \right)\frac{{\partial \Phi_{k} (q,t)}}{{\partial n_{q} }} \hfill \\ \end{gathered} \right]{\text{d}}S_{q} } \\ \hfill = \int_{0}^{t} {{\text{d}}\tau } \iint\limits_{{s_{b} }} {\left( \begin{gathered} \tilde{G}\left( {p,t;q,\tau } \right)\frac{{\partial \Phi_{k} (q,t)}}{{\partial n_{q} }} \hfill \\ - \Phi_{k} (q,t)\frac{{\partial \tilde{G}\left( {p,t;q,\tau } \right)}}{{\partial n_{q} }} \hfill \\ \end{gathered} \right){\text{d}}S_{q} }, \\ \end{gathered}$$

(47)

where $\Phi_{k}$ is the velocity potential which needs to be evaluated; the coordinates of field point $p$ and source point $q$ are $(x,y,z)$ and $(\xi ,\eta ,\zeta )$, respectively, with both lying in the water $(z \le 0)$; $R = \sqrt {(x - \xi )^{2} + (y - \eta )^{2} }$; $r = \sqrt {R^{2} + (z - \zeta )^{2} }$; $r^{\prime} = \sqrt {R^{2} + (z + \zeta )^{2} }$ represent the horizontal or the three-dimensional distance between field point $p$ and source point $q$ or the $q$’s image about the still water surface; $s_{b}$ is the wet surface of the floating structure; ${\mathbf{n}}_{q}$ is the unit normal vector of any source point on the wet surface; $\tilde{G}\left( {p,t;q,\tau } \right)$ is the memory term of the corresponding time domain Green function. Its expression [37] is

$$\tilde{G}\left( {p,q;t} \right) = 2\int_{0}^{\infty } {{\text{d}}k\sqrt {gk} \sin \left( {\sqrt {gk} t} \right)e^{{k\left( {z + \zeta } \right)}} J_{0} \left( {kR} \right)} ,$$

(48)

where $J_{0}$ is the Bessel function of the first kind with order 0.

The calculation method of Green function is based on Clement [38]. The memory of Green function is transformed into a fourth-order ordinary differential equation, and then the Runge–Kutta method is adopted to calculate the differential equation.

According to the method of Fual [39], Eq. (47) is decomposed into instantaneous part and memory part. The expressions of them are

$$\begin{gathered} \psi_{k} \left( p \right) + \frac{1}{2\pi }\iint\limits_{{s_{b} }} {\psi_{k} }\left( q \right)\frac{\partial }{{\partial n_{q} }}\left( {\frac{1}{r} - \frac{1}{{r^{\prime}}}} \right){\text{d}}S_{q} \hfill \\ = \frac{1}{2\pi }\iint\limits_{{s_{b} }} {\left( {\frac{1}{r} - \frac{1}{{r^{\prime}}}} \right)n_{k} {\text{d}}S_{q} } \hfill \\ \end{gathered}$$

(49)

$$\begin{aligned} \chi_{k} (p,t) & + \frac{1}{2\pi }\iint\limits_{{s_{b} }} {\chi_{k} (q,t)\frac{\partial }{{\partial n_{q} }}\left( {\frac{1}{r} - \frac{1}{{r^{\prime}}}} \right){\text{d}}S_{q} } \\ & \; = \frac{1}{2\pi }\iint\limits_{{s_{b} }} {n_{k} (q)\tilde{G}\left( {p,t;q,0} \right){\text{d}}S_{q} } \\ & \;\;\; - \frac{1}{2\pi }\iint\limits_{{s_{b} }} {\psi_{k} \left( q \right)\frac{\partial }{{\partial n_{q} }}\tilde{G}\left( {p,t;q,0} \right){\text{d}}S_{q} } \\ & \;\;\; - \frac{1}{2\pi }\int_{0}^{t} {{\text{d}}\tau } \iint\limits_{{s_{b} }} {\chi_{k} (q,\tau )\frac{{\partial \tilde{G}\left( {p,t;q,\tau } \right)}}{{\partial n_{q} }}{\text{d}}S_{q} }. \\ \end{aligned}$$

(50)

Equations (49) and (50) are, respectively, numerical discrete. Wet surface of the 3-d object is used by a series of quadrilateral grid to approximate. In each quadrilateral grid, the velocity potential is taken as a constant, and then the algebraic equation sets of instantaneous part and memory part are

$$\sum\limits_{j = 1}^{M} {A_{ij} \left( {\psi_{k} } \right)_{j} = B_{i} } \, i = 1,2, \ldots ,M$$

(51)

$$\sum\limits_{j = 1}^{M} {A_{ij} \left[ {\chi_{k} \left( {t_{N} } \right)} \right]_{j} = B\left( {t_{N} } \right)_{i} } \, i = 1,2, \ldots ,M,$$

(52)

where $M$ is the number of quadrilateral elements; $N$ is the current time steps;$\left( {\psi_{k} } \right)_{j}$ is the instantaneous part of the j element; $\left[ {\chi_{k} \left( {t_{N} } \right)} \right]_{j}$ is the memory part of the j element in the time of $t_{N}$; $A_{ij}$, $B_{i}$, and $B\left( {t_{N} } \right)_{i}$ are the coefficient matrixes, and the expressions are

$$A_{ij} = \left\{ \begin{gathered} \iint\limits_{{s_{j} }} {\frac{\partial }{{\partial n_{j} }}\left( {\frac{1}{{r_{ij} }} - \frac{1}{{r_{ij}^{\prime } }}} \right)}{\text{d}}S, \, i \ne j \hfill \\ 2\pi - \iint\limits_{{s_{j} }} {\frac{\partial }{{\partial n_{j} }}\left( {\frac{1}{{r_{ij}^{\prime } }}} \right)}{\text{d}}S, \, i = j \hfill \\ \end{gathered} \right.$$

(53)

$$B_{i} = \sum\limits_{j = 1}^{M} {\iint\limits_{{s_{j} }} {\left( {\frac{1}{{r_{ij} }} - \frac{1}{{r_{ij}^{\prime } }}} \right)\left( {n_{k} } \right)_{j} {\text{d}}S}}$$

(54)

$$\begin{aligned} B\left( {t_{N} } \right)_{i} & = \sum\limits_{j = 1}^{M} {\iint\limits_{{s_{j} }} {\left[ {n_{k} } \right]_{j} \tilde{G}\left( {p_{i} ,q_{j} ,t_{N} } \right){\text{d}}S}} \\ & \;\;\; - \sum\limits_{j = 1}^{M} {\iint\limits_{{s_{j} }} {\left[ {\psi_{k} } \right]_{j} \frac{\partial }{{\partial n_{j} }}\tilde{G}\left( {p_{i} ,q_{j} ,t_{N} } \right){\text{d}}S}} \\ & \;\;\; - \Delta t\sum\limits_{n = 1}^{N} {\sum\limits_{j = 1}^{M} {\iint\limits_{{s_{j} }} {\left[ {\chi_{k} \left( {q_{j} ,t_{n} } \right)} \right]_{j} \frac{\partial }{{\partial n_{j} }}\tilde{G}\left( {p_{i} ,q_{j} ,t_{N} - t_{n} } \right){\text{d}}S}} } , \\ \end{aligned}$$

(55)

where $\Delta t$ is the time step;$t_{N} = N\Delta t$; $t_{n} = n\Delta t$.

By the calculation of algebraic equation sets, the integral equations of added mass and memory function are

$$\mu_{ik} = \rho \iint\limits_{{s_{b} }} {\psi_{k} \left( q \right)n_{j} {\text{d}}S_{q} }$$

(56)

$$\overline{K}_{jk} \left( t \right) = \rho \iint\limits_{{s_{b} }} {\frac{\partial }{\partial t}\chi_{k} \left( {q,t} \right){\text{d}}S_{q} }$$

(57)

$$A_{jk} \left( \omega \right) = \mu_{jk} - \frac{1}{\omega }\int_{0}^{t} {K_{jk} \left( \tau \right)\sin \left( {\omega \tau } \right){\text{d}}\tau }$$

(58)

$$B_{jk} \left( \omega \right) = \int_{0}^{t} {K_{jk} \left( \tau \right)\cos \left( {\omega \tau } \right){\text{d}}\tau } ,$$

(59)

where$\overline{K}_{jk} \left( t \right)$ is the memory function;$A_{jk} \left( \omega \right)$ is the added mass;$B_{jk} \left( \omega \right)$ is the damping coefficient.

1.2 The damping matrix

The damping matrix assumption is related to the mass matrix and the restoring force matrix, which can be expressed as follows:

$$\Phi^{T} \left[ K \right]\Phi = \left[ {2\zeta_{i} \omega_{i} m_{i} } \right],$$

(60)

where$\Phi$ is the shape matrix, $\omega_{i}$ is the structure natural frequency, K is the damping matrix, $m_{i}$ is the modal mass, $m_{i} = \Phi^{T} \left[ M \right]\Phi$, and $\zeta_{i}$ is the dimensionless damping ratio of each mode, generally 0.05.

The solution of $\Phi$ and $\omega_{i}$:

For the undamped vibration:

$$M\ddot{Y} + KY = 0.$$

(61)

The characteristic determinant is

$$\left| {T - \lambda M} \right| = 0.$$

(62)

The characteristic vector $\left[ {\Phi_{1} ,\Phi_{2} \ldots \Phi_{n} } \right]$ and characteristic value $\left[ {\begin{array}{*{20}c} {\lambda_{1} } & {} & {} & {} \\ {} & {\lambda_{2} } & {} & {} \\ {} & {} & \ddots & {} \\ {} & {} & {} & {\lambda_{n} } \\ \end{array} } \right]$ are obtained:

$$\lambda_{i} = \omega_{i}^{2} \;\;\;\omega_{i} = \sqrt {\lambda_{i} } .$$

(63)

The modal mass is

$$\left[ {\begin{array}{*{20}c} {m_{1} } & {} & {} & {} \\ {} & {m_{2} } & {} & {} \\ {} & {} & \ddots & {} \\ {} & {} & {} & {m_{n} } \\ \end{array} } \right] = \left[ \Phi \right]^{T} \left[ M \right]\left[ \Phi \right].$$

(64)

The K matrix can be obtained by solving the following matrix equation:

$$\Phi^{T} \left[ c \right]\Phi = 2\xi_{i} \left[ {\begin{array}{*{20}c} {\sqrt {\lambda_{1} } } & {} & {} & {} \\ {} & {\sqrt {\lambda_{2} } } & {} & {} \\ {} & {} & \ddots & {} \\ {} & {} & {} & {\sqrt {\lambda_{n} } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {m_{1} } & {} & {} & {} \\ {} & {m_{2} } & {} & {} \\ {} & {} & \ddots & {} \\ {} & {} & {} & {m_{n} } \\ \end{array} } \right].$$

(65)

Wave Force

2.1 Froude–Krylov force

Froude–Krylov force is caused by the incident potential, and its expression is

$$F_{jI} \left( t \right) = \iint\limits_{{s_{b} }} {p\left( {q,t} \right)n_{j} {\text{d}}S_{q} },$$

(66)

where $F_{jI}$ is the Froude–Krylov force in the $j\left( {j = 1,2, \ldots 6} \right)$ mode of motions. $n_{j}$ is the unit surface normal vector.

The expression [40] of the dynamic pressure acting on the floating structure by the incident waves is

$$p\left( {p,t} \right) = \int_{ - \infty }^{ + \infty } {\hat{p}\left( {p,t - \tau } \right)\zeta_{0} \left( \tau \right){\text{d}}\tau } ,$$

(67)

where $\hat{p}\left( {p,t} \right)$ is the impulse response function of pressure. The expression is

$$\hat{p}\left( {p,t} \right) = \frac{\rho g}{\pi }{\text{Re}} \left\{ {\int_{0}^{\infty } {e^{{k\left( {z - i\alpha } \right)}} e^{i\omega t} {\text{d}}\omega } } \right\}.$$

(68)

When the incident wave is a regular wave per unit wavelength, $\zeta_{0} \left( t \right) = e^{i\omega t}$.

2.2 Diffraction force

The diffraction force is mainly caused by the diffraction potential, and its expression is

$$\begin{aligned} 2\pi \hat{\Phi }_{7} (p,t) & + \iint\limits_{{s_{b} }} {\hat{\Phi }_{7} (q,t)\frac{\partial }{{\partial n_{q} }}\left( {\frac{1}{r} - \frac{1}{{r^{\prime}}}} \right){\text{d}}S_{q} } \\ & = - \iint\limits_{{s_{b} }} {\left( {\frac{1}{r} - \frac{1}{{r^{\prime}}}} \right)\left[ {{\vec{\mathbf{n}}} \cdot \hat{K}\left( {q,t} \right)} \right]{\text{d}}S_{q} } \\ & \;\;\; - \int_{0}^{t} {{\text{d}}\tau } \iint\limits_{{s_{b} }} {\left\{ \begin{gathered} \tilde{G}\left( {p,t;q,\tau } \right)\left[ {{\vec{\mathbf{n}}} \cdot \hat{K}\left( {q,t} \right)} \right] \hfill \\ + \hat{\Phi }_{7} \left( {q,\tau } \right)\frac{{\partial \tilde{G}\left( {p,t;q,\tau } \right)}}{{\partial n_{q} }} \hfill \\ \end{gathered} \right\}{\text{d}}S_{q} }, \\ \end{aligned}$$

(69)

where the impulse response function $\hat{K}\left( {p,t} \right)$ is

$$\hat{K}\left( {p,t} \right) = \frac{1}{\pi }{\text{Re}} \left\{ {\left[ \begin{gathered} {\vec{\mathbf{i}}}\cos \beta \hfill \\ {\vec{\mathbf{j}}}\sin \beta \hfill \\ {\vec{\mathbf{k}}}i \hfill \\ \end{gathered} \right]\int_{0}^{\infty } {e^{{k\left( {z - i\alpha } \right)}} e^{i\omega t} {\text{d}}\omega } } \right\}.$$

(70)

The calculation method of diffraction potential is the same as that of radiation potential. By solving the integral equation of the diffraction potential, the expression of diffraction force is

$$F_{j7} = \int_{ - \infty }^{\infty } {\zeta_{0} \left( \tau \right){\text{d}}\tau \left[ { - \rho \iint\limits_{{s_{b} }} {\frac{\partial }{\partial t}\hat{\Phi }_{7} \left( {q,t - \tau } \right)n_{j} {\text{d}}S_{q} }} \right]} .$$

(71)

2.3 Drag force

For slender columns, the influence of the drag force on the platform can be calculated by the Morison equation, and the drag force per unit length of column is

$$f_{{\text{D}}} = \frac{1}{2}\rho C_{D} D\left( {w_{x} - \dot{x}} \right)\left| {\left( {w_{x} - \dot{x}} \right)} \right|,$$

(72)

where $D$ is the diameter of column;$C_{{\text{D}}}$ is the coefficient of drag force;$w_{x}$ is horizontal component of the velocity of the fluid particle;$\dot{x}$ is the velocity of floating structure.

The determination method of drag force coefficient [36] is

$$C_{{\text{D}}} = \left\{ \begin{gathered} 60.566 - 5.93{\text{Re}} {\text{ Re}} \le 10 \hfill \\ 1.25{\text{ 10 < Re}} \le 5 \times 10^{5} \hfill \\ 0.7 \, {\text{Re}} > 5 \times 10^{5} \hfill \\ \end{gathered} \right.,$$

(73)

where Re is the Reynolds number that is ${\text{Re}} = UD/\nu$. $U$ is the relative velocity of fluid. D is characteristic length. In this paper, $D$ is the diameter of column. $\nu$ is the coefficient of kinematic viscosity, which is 1.346e−6 m²/s when the temperature of seawater is 10 °C.

The velocity of fluid particle is calculated by Airy linear wave theory. The velocity of water particle (x direction) is

$$w_{{x^{\prime}}} = \frac{{\pi W_{{\text{H}}} }}{{W_{{\text{T}}} }}\frac{{\sinh \left( {kx} \right)}}{{\sinh \left( {kd} \right)}}\sin \left( {kz - \omega t} \right).$$

(74)

The velocity of water particle (y direction) is

$$w_{{y^{\prime}}} = 0.$$

(75)

The velocity of water particle (z direction) is

$$w_{{z^{\prime}}} = \frac{{\pi W_{{\text{H}}} }}{{W_{{\text{T}}} }}\frac{{\cosh \left( {kx} \right)}}{{\sinh \left( {kd} \right)}}\cos \left( {kz - \omega t} \right),$$

(76)

where $W_{{\text{H}}}$ is the wave height;$W_{{\text{T}}}$ is the wave period; k is the wave number;$\omega$ is the wave frequency; and d is the depth of water.

According to method of the coordinate transformation, transforms the particle velocity in the wave coordinate system $O^{\prime}X^{\prime}Y^{\prime}Z^{\prime}$ to the static coordinate system OXYZ:

$$\left\{ \begin{gathered} w_{x} = w_{{x^{\prime}}} \cos \alpha \hfill \\ w_{y} = w_{{y^{\prime}}} \cos \alpha \hfill \\ w_{z} = w_{{z^{\prime}}} \hfill \\ \end{gathered} \right.$$

(77)

$\alpha$ is the angle between the coordinate system $O^{\prime}X^{\prime}Y^{\prime}Z^{\prime}$ and the static coordinate system OXYZ.

The relative velocity between water particle and floating structure in the static coordinate system OXYZ is

$$\vec{V} = \left( {\dot{x}_{1} \vec{i} + \dot{x}_{2} \vec{j} + \dot{x}_{3} \vec{k}} \right) + \vec{\omega } \times \vec{r}$$

(78)

$$\vec{r} = x_{1} \vec{i} + x_{2} \vec{j} + x_{3} \vec{k},$$

(79)

where $\vec{\omega } \times \vec{r} = \left| {\begin{array}{*{20}c} {\vec{i}} & {\vec{j}} & {\vec{k}} \\ {\dot{x}_{4} } & {\dot{x}_{5} } & {\dot{x}_{6} } \\ {x_{1} } & {x_{2} } & {x_{3} } \\ \end{array} } \right|$, and substitute it into Eq. 78. Then the relative velocity is

$$\begin{gathered} \vec{w}_{r} = w_{rx} \vec{i} + w_{ry} \vec{j} + w_{rz} \vec{k} \\ = \left[ {w_{x} - \left( {\dot{x}_{5} x_{3} - \dot{x}_{6} x_{2} + \dot{x}_{1} } \right)} \right]\vec{i} \\ + \left[ {w_{y} - \left( { - \dot{x}_{4} x_{3} + \dot{x}_{6} x_{1} + \dot{x}_{2} } \right)} \right]\vec{j} \\ + \left[ {w_{z} - \left( {\dot{x}_{4} x_{2} - \dot{x}_{5} x_{1} + \dot{x}_{3} } \right)} \right]\vec{k}. \\ \end{gathered}$$

(80)

The wet surface of the platform is separated into a series of differential rings, and the centers of the circles are taken as the discrete points. Based on the Morison equation, the drag force calculating formula in the case of the i discrete element is

$$\left[ \begin{gathered} F_{Dxi} \hfill \\ F_{Dyi} \hfill \\ F_{Dzi} \hfill \\ \end{gathered} \right] = \frac{1}{2}\rho C_{{\text{D}}} D\left( \begin{gathered} w_{rxi} \hfill \\ w_{ryi} \hfill \\ w_{rzi} \hfill \\ \end{gathered} \right)\left| \begin{gathered} w_{rxi} \hfill \\ w_{ryi} \hfill \\ w_{rzi} \hfill \\ \end{gathered} \right|$$

(81)

The calculation formula of the drag forces of the platform in waves is

$$\left\{ \begin{gathered} F_{Dx} \hfill \\ F_{Dy} \hfill \\ F_{Dz} \hfill \\ \end{gathered} \right. = \left\{ \begin{gathered} \sum\limits_{i = 1}^{N} {F_{Dxi} } \hfill \\ \sum\limits_{i = 1}^{N} {F_{Dyi} } \hfill \\ \sum\limits_{i = 1}^{N} {F_{Dzi} } \hfill \\ \end{gathered} \right.,$$

(82)

where N is the number of discrete elements on the platform.

The calculation formula of the drag moments of the platform in waves is

$$\left\{ \begin{gathered} M_{Dx} = F_{Dz} y - F_{Dy} z \hfill \\ M_{Dy} = F_{Dx} z - F_{Dz} x \hfill \\ M_{Dz} = F_{Dy} x - F_{Dx} y \hfill \\ \end{gathered} \right..$$

(83)

When the relative velocities are calculated, the velocities of the platform are required. Therefore, the formulas of wave drag forces are linked with the differential motion equations of the floating structure and the time iteration of the differential equations is carried out. Then the drag forces of waves on the platform can be calculated.

2.4 Second-order wave forces

The wave force on the platform includes not only the first-order wave force calculated above, but also the second-order wave force. The second-order wave forces consist mainly of the mean drift force, the sum frequency wave force, and the differential frequency wave force [20].

There are two methods of calculating the mean drift force, including the near-field method and the far-field method, respectively. The near-field method is based on the direct solution of the waterline surface and object area components to obtain the average drift force for the six degrees of freedom of the platform. The far-field method is achieved mainly through the law of conservation of energy, while the far-field method can only result in the calculation of the platform's component in the horizontal plane. The near-field and far-field formulations of the mean drift force are given separately [26].

Near-field equation for mean drift force.

$$F_{{{\text{d}}x}} = - \frac{\rho }{2}\left\{ {\iint_{{S_{{\text{H}}} }} {\left[ {\phi_{1} \frac{\partial }{\partial n}\left( {\frac{{\partial \phi_{1} }}{\partial x}} \right) - \frac{{\partial \phi_{1} }}{\partial x}.\frac{{\partial \phi_{1} }}{\partial n}} \right]}{\text{d}}s} \right\}_{m}$$

(84)

$$F_{{{\text{d}}y}} = - \frac{\rho }{2}\left\{ {\iint_{{S_{{\text{H}}} }} {\left[ {\phi_{1} \frac{\partial }{\partial n}\left( {\frac{{\partial \phi_{1} }}{\partial y}} \right) - \frac{{\partial \phi_{1} }}{\partial y}.\frac{{\partial \phi_{1} }}{\partial n}} \right]}{\text{d}}s} \right\}_{m} .$$

(85)

Far-field equation for mean drift force.

$$F_{{{\text{d}}x}} = - \frac{\rho }{2g}\left\{ {\int_{{l_{0} }} {\left( {\frac{{\partial \phi_{1} }}{\partial t}} \right)^{2} n_{x} {\text{d}}l} } \right\}_{m} - \rho \left\{ {\iint_{{C_{0} }} {\left[ {\frac{{\partial \phi_{1} }}{\partial x}.\frac{{\partial \phi_{1} }}{\partial n} - \frac{1}{2}\left( {\nabla \phi_{1} } \right)^{2} n_{x} } \right]}{\text{d}}s} \right\}_{m}$$

(86)

$$F_{{{\text{d}}y}} = - \frac{\rho }{2g}\left\{ {\int_{{l_{0} }} {\left( {\frac{{\partial \phi_{1} }}{\partial t}} \right)^{2} n_{y} {\text{d}}l} } \right\}_{m} - \rho \left\{ {\iint_{{C_{0} }} {\left[ {\frac{{\partial \phi_{1} }}{\partial y}.\frac{{\partial \phi_{1} }}{\partial n} - \frac{1}{2}\left( {\nabla \phi_{1} } \right)^{2} n_{y} } \right]}{\text{d}}s} \right\}_{m} .$$

(87)

As the near-field formulation of the mean drift force can calculate the motion of the platform in six degrees of freedom, while the far-field formulation can only calculate the surge, sway and yaw motions, this paper focuses on the effect of the mean drift force calculated by the near-field method on the motion response of the TLP.

The expression for the second-order force [26] can be expressed as

$$F^{\left( 2 \right)} = \frac{1}{2}\rho g\int_{\Gamma 0} {\eta^{{\left( 1 \right)^{2} }} n{\text{d}}\Gamma - \rho \iint\limits_{S} {\left( {\phi_{t}^{\left( 2 \right)} + \frac{1}{2}\left( {\nabla \phi^{\left( 1 \right)} } \right)^{2} } \right)}n{\text{d}}S} .$$

(88)

The above equation is bounded using second-order bypassing-radiation theory, and the standard form of the second-order force calculation equation

$$\begin{gathered} F^{\left( 2 \right)} \left( t \right) = A_{1}^{2} f_{{\text{d}}} \left( {\omega_{1} } \right) + h\left\{ {A_{1}^{2} + f_{ + }^{\left( 2 \right)} \left( {\omega_{1} ,\omega_{1} } \right)e^{{ - 2i\omega_{1} t}} + } \right.A_{2}^{2} f_{ + }^{\left( 2 \right)} \left( {\omega_{2} ,\omega_{2} } \right)e^{{ - 2i\omega_{2} t}} \\ \left. {{ + }2A_{1} A_{2} f_{ - }^{\left( 2 \right)} \left( {\omega_{1} ,\omega_{2} } \right)e^{{ - 2i\left( {\omega_{1} - \omega_{2} } \right)t}} + 2A_{1} A_{2} f_{ + }^{\left( 2 \right)} \left( {\omega_{1} ,\omega_{2} } \right)e^{{ - 2i\left( {\omega_{1} + \omega_{2} } \right)t}} } \right\} + A_{2}^{2} f_{{\text{d}}} \left( {\omega_{2} } \right), \\ \end{gathered}$$

(89)

where$f_{{\text{d}}}$ is the normalized mean drift force; $f_{ + }^{\left( 2 \right)}$ is the second-order transfer function (QTF) of the normalized sum frequency force; $f_{ - }^{\left( 2 \right)}$ is the second-order transfer function (QTF) of the normalized difference frequency force; $\omega_{1}$ and are the $\omega_{2}$ wave frequencies of the two incident waves; $A_{1}$ and $A_{2}$ are the wave amplitudes of the two incident waves, respectively.

In this paper, the frequency domain solution of the second-order force is calculated based on the HydroD module, including the average drift force $f_{{\text{d}}}$ and the second-order transfer function (QTF) of the sum frequency force and differential frequency force, respectively, and embedded in the coupled TLP model compiled in this paper to obtain the TLP motion responses under the influence of the second-order wave forces.